2. 西安交通大学智能网络与网络安全教育部重点实验室, 陕西 西安 710049;
3. 清华大学精密仪器系类脑计算研究中心, 北京 100084;
4. 青岛星跃铁塔有限公司, 山东 青岛 266300
2. Ministry of Education Key Lab For Networks and Network Security, Xi'an Jiaotong University, Xi'an 710049, China;
3. Center for Brain Inspired Computing Research, Department of Precision Instrument, Tsinghua University, Beijing 100084, China;
4. Qingdao Xingyue Iron Tower Co., Ltd, Qingdao 266300, China
0 引言
近年来,随着多智能体系统的协同控制在信息控制[1]、编队控制[2]、群集运动[3]等方面的广泛应用,已引起越来越多研究人员的关注.其中,一致性问题[1-4]作为协同控制的核心问题,更是得到了广泛的关注.多智能体一致性问题主要是研究多智能体系统中个体之间通过有限的信息交换,使所有智能体的状态达到某同一值的行为.在实际工程应用中,多智能体之间的信息交换因受到距离、障碍、干扰等多种不确定性因素的影响,会导致通信链路的中断或重建,使多智能体之间信息交换的准确性降低.通常使用切换拓扑来描述这种通信链路的改变.常见的切换拓扑有固定时间切换拓扑[5]和随机时间切换拓扑,而随机时间切换拓扑又可分为任意切换拓扑[6]、随机切换拓扑[7]和马尔可夫切换拓扑,其中马尔可夫切换拓扑包含任意和随机切换拓扑的特性更具一般性[8].因此,本文研究马尔可夫切换拓扑下多智能体系统的一致性.
目前,针对切换拓扑下线性多智能体一致性已经有诸多研究[9-12].文[9]研究了带有多种噪声干扰的马尔可夫切换拓扑下的一阶多智能体系统,设计了一致性协议,使系统分别实现均方平均趋同和概率1平均趋同.文[10]研究了当领导者状态为时不变时,马尔可夫切换拓扑下二阶多智能体系统的领导—跟随一致性.文[11-12]研究了马尔可夫切换拓扑下高阶多智能体系统的一致性问题,并指出系统实现一致性的条件是联合切换拓扑包含有向生成树.
上述研究都是针对线性系统,然而,自然界中几乎所有的物理系统都是非线性的,比如异步电动机系统[13]、飞控系统[14]和电力系统[15],因此,研究非线性多智能体一致性更具应用价值.针对非线性多智能体一致性的研究也取得了很多成果[16-22].文[16]以一阶非线性系统为研究对象,文[17-18]研究了二阶非线性系统,事实上,很多物理系统具有高阶性的特点,高阶非线性系统也成为目前的研究热点.文[19]设计了动态输出一致性协议,研究了无向网络下,一类高阶非线性多智能体系统的领导—跟随一致性.文[20]提出了确定有向网络中最小数量领导者的方法,并设计了控制协议保证高阶时变非线性多智能体系统的一致性.更进一步,为了解决具有不同和未知的非线性多智能体系统的一致性问题,文[21-22]设计了自适应的一致性协议.与此同时,也需要考虑干扰、拓扑切换等对非线性多智能体一致性的影响.
针对切换拓扑下非线性多智能体一致性也有诸多研究[23-26].文[23]解决了具有通信时延的马尔可夫切换拓扑下高阶非线性多智能体系统的领导—跟随一致性问题,但其联合切换拓扑是无向连通的.文[24]对切换拓扑下非线性多智能体系统的领导—跟随一致性进行研究,但要求每个时刻的通信拓扑结构均包含有向生成树,且只讨论了两个拓扑在固定时间内切换.文[25]放宽了通信拓扑连接的限制,考虑部分时刻的拓扑结构包含有向生成树.文[26]得出了和线性系统相似的结论,指出实现马尔可夫切换拓扑下非线性多智能体系统一致性的条件是联合切换拓扑包含有向生成树.文[23]是针对无向通信网络.文[24-25]虽然是针对有向切换拓扑,但分别要求每一时刻和部分时刻的通信拓扑包含有向生成树.文[26]放宽了限制条件,只需联合切换拓扑包含有向生成树.分析上述研究成果可知,目前对切换拓扑下非线性多智能体系统一致性的研究中,仍对联合切换拓扑有限制,至少需要联合切换拓扑包含有向生成树,然而在大规模网络环境中确保网络的连通性仍是亟待解决的问题.在一般有向切换拓扑结构的通信条件下保证系统的一致性,更具实际意义.
本文考虑联合切换拓扑是任意有向网络结构,研究了马尔可夫切换拓扑下高阶非线性系统的一致性.相比于已有的研究成果,本文的创新之处在于:1)本文不需要对通信拓扑进行限制,考虑联合切换拓扑是任意有向网络结构;2)本文针对马尔可夫切换拓扑下高阶非线性系统设计了具有动态增益的一致性协议.
1 问题描述符号和定义:用G={v,ε}表示由N个智能体组成的有向图,其中v={1,2,…,N}是图的顶点集合,ε⊆v×v是图的边集.有向图G的权值邻接矩阵为Λ=[aij]∈RN×N,其中aij=1表示节点i可以接收到节点j的信息,否则aij=0.有向图G的入度矩阵表示为D=diag(d1,d2,…,dN),其中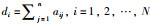
本文用图G表示跟随者智能体之间的网络拓扑,用图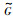
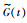
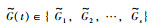
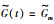
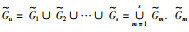
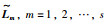
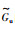
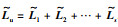
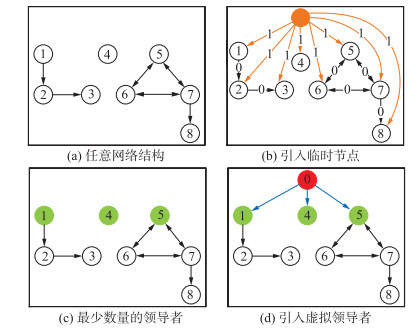
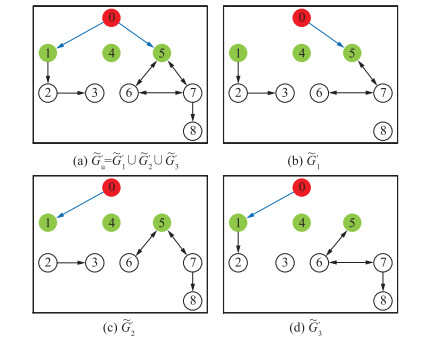
本文针对联合切换拓扑是任意网络拓扑结构的多智能体系统一致性问题进行研究.由文[9-12, 26]可知,切换拓扑下的多智能体系统实现一致性的条件是联合切换拓扑包含有向生成树.若联合切换拓扑是任意网络结构,特别是具有孤立的节点,如图 1(a)所示,则不能实现系统的一致性.因此,需要先对联合切换拓扑进行构造,使构造后的网络结构包含有向生成树.
|
| 图 1 构造联合切换拓扑 Fig.1 Constructing the union of switching topologies |
本文借鉴文[20]的研究思想,研究马尔可夫切换拓扑下多智能体系统的一致性问题.图 1显示了对联合切换拓扑的构造过程,分两步进行:1)引入临时节点,如图 1(b)所示,通过最小树形图理论[25]找到任意网络结构中最少数量的领导者,结果如图 1(c);2)引入虚拟领导者与定位最少数量领导者相连,图 1(d)即为构建后的联合切换拓扑.
引理1[20] 对于任意的有向网络Gu,找到最少数量的领导者,建立虚拟领导者与定位的最少数量的领导者相连,连接后的有向网络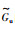
注1 文[26]证明了马尔可夫切换拓扑下非线性多智能体系统实现一致性的条件是联合切换拓扑包含有向生成树.本文针对联合切换拓扑可以是任意网络结构的多智能体系统进行研究,给出了将联合切换拓扑构造为有向生成树的方法,其应用更具普适性.
1.2 拓扑切换过程描述用连续时间马尔可夫过程描述切换过程{σ(t),t≥0},它在有限的状态集合{1,2,…,s}上取值,其转移密度矩阵为Q=[qij]s×s∈Rs×s.连续时间马尔可夫过程的转移概率密度表示为
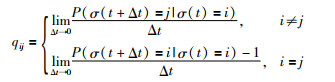
|
其中,i,j∈s,t∈R+,qij表示从状态i到状态j的转移概率密度,表示状态发生转换的速度,qij≥0且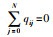
引理2[4] f(t)是Ft的测度,假定E{f(t)1{σ(t)=i}}= fi(t)存在,其中,1{σ(t)=i}是集合{σ(t)=i}上的迪拉克测度.对于i∈s,下式成立:
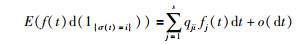
|
(1) |
其中,o(dt)表示dt的高阶无穷小.
1.3 多智能体模型在引入虚拟领导者节点与任意网络结构的最少数量的领导者相连后,将联合切换拓扑为任意网络结构的多智能体系统的一致性问题转化为虚拟领导者节点和多智能体系统的领导—跟随一致性问题.这里,构造的联合切换拓扑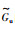
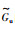
考虑由N个跟随者智能体和一个虚拟领导者智能体组成的具有非线性动态模型为
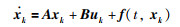
|
(2) |
其中,k=0表示虚拟领导者智能体,k=1,2,…,N表示跟随者智能体;xk=[xk,1,xk,2,…,xk,n]T是第k个智能体的状态;A和B是任意常数矩阵;uk,k=1,2,…,N是需要设计的控制协议,u0是给出的虚拟领导者智能体的控制协议;f(·)=[f1,f2,f3,…,fn]T,fi是时间t和状态xk,1,xk,2,…,xk,i(i=1,2,…,n)的函数.
定义1 在任何有限初始状态x0下,存在正数C和t0,使:
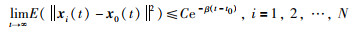
|
(3) |
称以速度β实现领导—跟随一致.
为了使系统实现领导—跟随一致性,引入如下的假设和引理.
假设1[27] 对i=1,2,…,n,存在非负实数c1和c2,使非线性函数f(x)满足如下的Lipschitz条件:
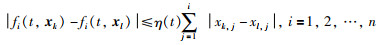
|
(4) |
其中,η(t)=c1ec2t.
注2 η(t)是定义在[0,+∞)上任何已知的指数函数.通过选取适当的c1和c2,指数函数c1ec2t可以作为许多时变函数的边界.因此,满足假设1的系统(2)包含了许多类型的时变系统.
引理3[19] 图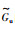
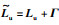
引理4[27] 存在行向量K=[k1,k2,…,kn],使得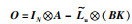

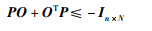
|
(5) |
注3 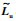
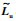
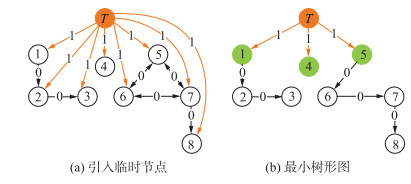
对于任意网络结构Gu,引入一个临时节点T与每一个结点连接构成拓扑图G*.在拓扑图G*中,令连接临时节点T的有向边,权值置1,如不连接临时节点,权值置0,如图 2(a)所示.由文[20]可知,寻找拓扑图G的最少数量领导者问题可转化为寻找图G*的最小树形图问题,从而可使用朱刘算法[28]解决.在图G*的最小树形图中,与临时节点T相连的节点,即为图Gu的最少数量领导者节点,如图 2(b)所示,节点1、节点4、节点5即为图 1(a)所示网络拓扑的最少数量的领导者.
|
| 图 2 寻找最小树形图 Fig.2 Finding the minimum arborescence in a network |
对有向图G*(ν,ε),求其最小树形图的算法过程如下:
步骤1:对除根节点以外的N-1个节点,选择权值最小的输入有向边,构成有向边集s.若没有形成环,G*(ν,s)即为最小树形图;否则,转到步骤2.
步骤2:将每一个环中的节点收缩为一个伪节点m,修改每条从环外节点i指向环内节点j的有向边的权值:
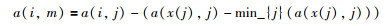
|
其中,a(x(j),j)是有向环内指向j的权值.
步骤3:对每个伪节点和实节点,选择权值最小的输入有向边.若有环,转到步骤2;否则,转到步骤4.
步骤4:记录当前的有向边,展开收缩点,去除环中与记录的有向边相同终点的边.
2.2 设计一致性协议若拓扑结构为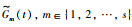
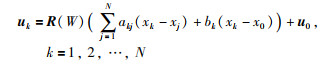
|
(6) |
其中,R(·)∈R1×n将在之后确定,W(t)是时变方程,在t≥0时,都有W(t)≥1.在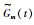
定义一致性误差为
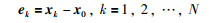
|
(7) |
由系统(2),式(7)可写为
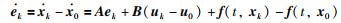
|
(8) |
若一致性误差(8)在有限时间内收敛到零,则系统(2)可实现一致性.为了求解一致性协议中的时变参数W,对每个智能体的一致性误差进行如下状态变换:
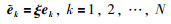
|
(9) |
其中,ξ=diag(Wn,Wn-1,…,W).
由式(9)和一致性误差(8),可得:
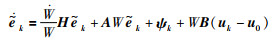
|
(10) |
其中,H=diag(n,n-1,…,1),k=1,2,…N,ψk= ξ(f(t,xk)-f(t,x0)).
因此,求解一致性误差(8)的稳定性问题又可转换为求取时变参数W保证系统(10)的稳定性问题.为求解系统(10)的稳定性,引入如下定理.
定理1 存在时变参数W(t),使系统(10)的稳定性可通过如下的一致性协议解决:
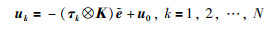
|
(11) |
其中,τk是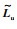
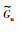
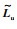
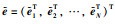
证明:由系统(10)和一致性协议(11),可以得到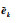
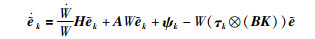
|
(12) |
考虑到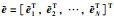
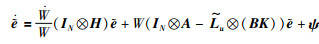
|
(13) |
其中,ψ=[ψ1T,ψ2T,…,ψNT]T.
定义李亚普诺夫函数V(t):
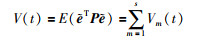
|
(14) |
其中,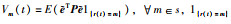
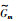
由引理2,Vm(t)的导数可以写为
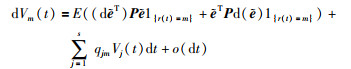
|
(15) |
将式(13)代入式(15),得到
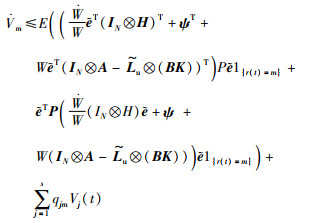
|
(16) |
由于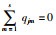
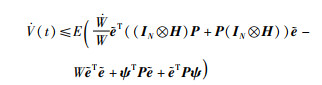
|
(17) |
进一步可得:
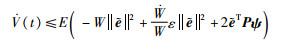
|
(18) |
其中,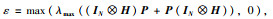
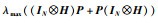
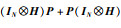
由假设1和式(9),可得:
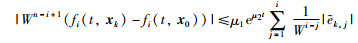
|
(19) |
其中,i=1,2,…,n,k=1,2,…,N.当t≥0时,都有W(t)≥1,式(19)可进一步写为
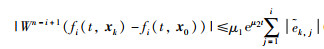
|
(20) |
因此,
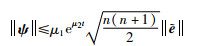
|
(21) |
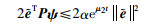
|
(22) |
其中,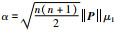
将式(21)代入式(18)可得:
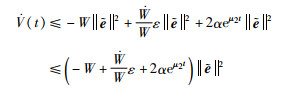
|
(23) |
为了满足系统(10)稳定性,令:
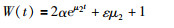
|
(24) |
进一步可以得到:
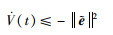
|
(25) |
令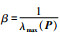
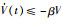
进一步可以得到:
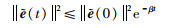
|
(26) |
即,进行状态变换后的系统(10)满足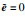
接下来,对状态变换前的一致性误差(8)的稳定性,即,系统(2)的一致性进行说明.
定理2 在假设1的条件下,如果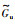
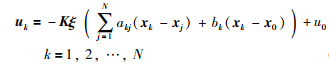
|
(27) |
其中,ξ=diag(Wn,Wn-1,…,W),K可由引理4得到.
证明:由式(23)可知,t≥0时,W(t)≥1,对角矩阵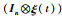
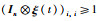
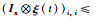
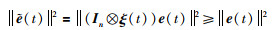
|
(28) |
当t=0时,有:
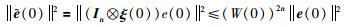
|
(29) |
其中,W(0)=2α+εμ2+1.
由式(25)可以得到:
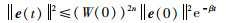
|
(30) |
因此,一致性误差e=0,在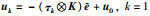
对于系统(2),一致性协议的设计步骤如下:
步骤1:引入临时节点与任意网络拓扑的每个节点连接,将连接临时节点的有向边,权值置1,若没有连接,权值置0.
步骤2:通过朱刘算法,对步骤1的有向图求最小树形图,标记与临时节点相连的节点,并引入虚拟领导者与其相连.
步骤3:通过引理4获得K和P.
步骤4:通过假设1和从步骤3解出的K和P,根据式(18)~式(23)确定参数ε和α.
步骤5:通过步骤4获得的参数ε和α,由式(24)求解出W(t).
步骤6:通过步骤3和5获得K和W(t),得到系统(2)的一致性协议(27).
3 数值仿真本节通过具体实例来证明马尔可夫切换拓扑下时变非线性多智能体系统(2)在一致性协议(27)下的领导—跟随一致性.
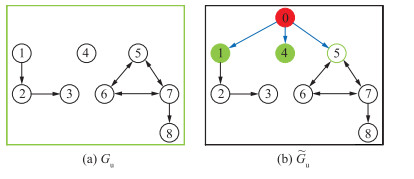
考虑如图 3(a)所示的联合切换拓扑图Gu,使用朱刘算法可以确定最少数量的领导者为节点1、节点4和节点5,建立一个虚拟领导者结点0与节点1、节点4和节点5连接,构造的联合切换拓扑图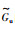
|
图 3 联合切换拓扑图Gu和构造的联合切换拓扑图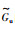 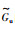 |
选择系统参数: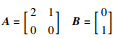
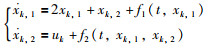
|
(31) |
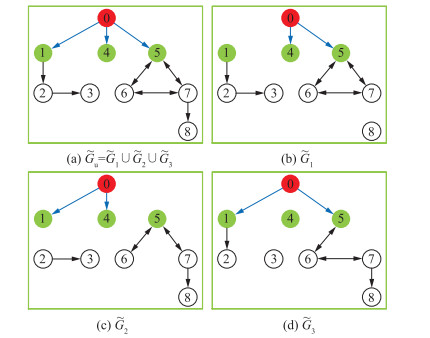
其中,k=0,1,…,8,第k个智能体的状态是xk=[xk,1,xk,2]T∈R2,控制输入为uk∈R2.索引为0表示领导者智能体,索引为1,2,3,4,5,6,7,8表示跟随者智能体.多智能体系统在图 4所示的拓扑结构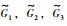
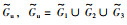
|
| 图 4 联合切换拓扑包含有向生成树的网络拓扑图 Fig.4 A network topologiy with the union of switching topologies includes a directed spanning tree |
通过本文的设计算法,选取控制增益K=[5 5],系统(31)的领导—跟随一致性协议可以设计为
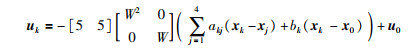
|
其中,k=1,2,…,8.令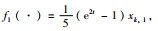
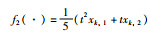
用连续时间的马尔可夫过程mt来描述拓扑切换过程,mt的状态空间为S={1,2,3},状态转移密度矩阵为Q= 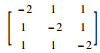
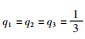
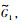
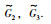
|
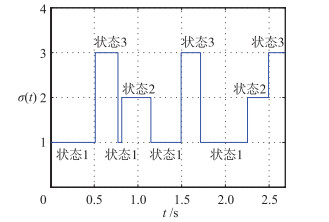
| 图 5 网络拓扑的切换信号 Fig.5 Switching signal for network topology |
随机给定多智能体系统的初始状态为:X(0)=[x0T,x1T,x2T,x3T,x4T,x5T,x6T,x7T,x8T]=[0, -1, -2, -4, -6, -8, -6, -4, -2, 0, 1, 2, 4, 6, 8, 6, 4, 2],系统的拓扑结构随着图 5所示的拓扑状态切换信号在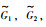
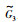
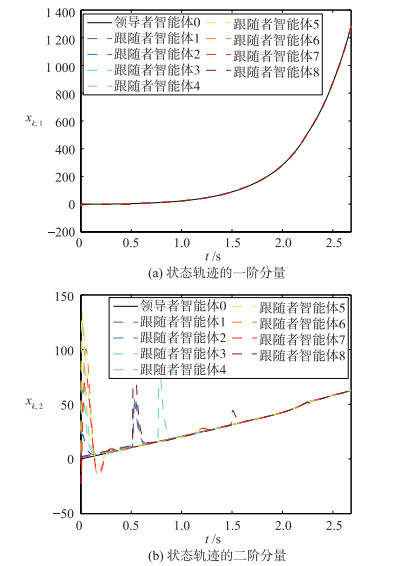
|
| 图 6 系统的状态轨迹变化(构造的联合切换拓扑包含有向生成树) Fig.6 The states trajectories with the switching topology (the constructed network topology includes a direct spanning tree) |
当构造的联合切换拓扑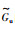
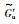
|
| 图 7 联合切换拓扑不包含生成树的网络拓扑图 Fig.7 A network topology with the union of switching topologies doesn′t include a directed spanning tree |
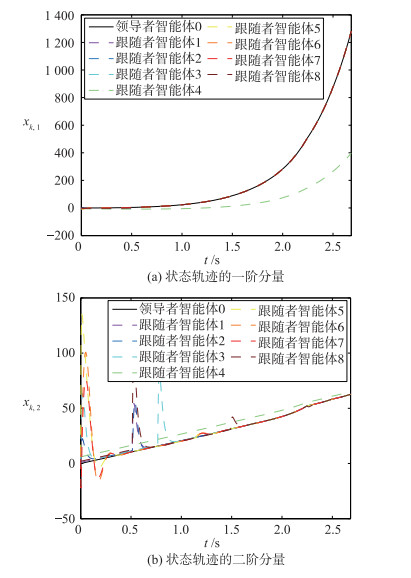
多智能体系统的状态轨迹如图 8所示,可以看出,跟随者智能体4的状态轨迹未收敛到领导者智能体的状态轨迹,其余智能体状态收敛到领导者智能体状态.因智能体4在3种拓扑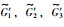
|
| 图 8 系统的状态轨迹变化(构造的联合切换拓扑不包含有向生成树) Fig.8 The states trajectories with the switching topology (the constructed network topology doesn′t include a direct spanning tree) |
本文研究了马尔可夫切换拓扑下时变非线性多智能体系统的领导—跟随一致性问题.首先,通过引入一个临时节点与任意网络结构中每一个智能体相连,将寻找最少数量的领导者问题转化为构建最小树形图问题,进而利用朱刘算法进行求解.接着,建立一个虚拟领导者连接所选取的最少数量的领导者,所构建的多智能体网络包含有向生成树,确保了多智能体系统的一致性.然后,设计了具有动态控制增益的一致性协议,通过引入一致性误差和状态变换,将具有动态增益的一致性协议的设计问题转化为动态参数的设计问题进行求解.最后,数值仿真结果验证了所提出的一致性协议能够使虚拟领导者与多智能体系统的状态实现全局一致,进一步证明了所提方法的有效性.
| [1] | Liu Y Y, Slotine J J, Barabasi A L. Controllability of complex networks[J]. Nature, 2011, 473(7346): 167. DOI:10.1038/nature10011 |
| [2] | Dong X, Yu B, Shi Z, et al. Time-varying formation control for unmanned aerial vehicles:Theories and applications[J]. IEEE Transactions on Control Systems Technology, 2015, 23(1): 340–348. DOI:10.1109/TCST.2014.2314460 |
| [3] | Gazi V. Stability of an asynchronous swarm with time-dependent communication links[J]. IEEE Transactions on Systems, Man and Cybernetics-Part B, 2008, 38(1): 267–274. DOI:10.1109/TSMCB.2007.910530 |
| [4] | Fragoso M D, Costa O L V. A unified approach for stochastic and mean square stability of continuous-time linear systems with Markovian jumping parameters and additive disturbances[J]. Proceedings of the IEEE Conference on Decision and Control, 2005, 44(4): 1165–1191. |
| [5] |
余莹莹, 方华京.
多智能体系统的有限时间跟踪控制[J]. 系统工程与电子技术, 2011, 33(8): 1871–1874.
She Y Y, Fang H J. Finite-time tracking control for multi-agent systems[J]. Journal of Systems Engineering and Electronics, 2011, 33(8): 1871–1874. DOI:10.3969/j.issn.1001-506X.2011.08.36 |
| [6] | Zhu W, Cheng D. Leader-following consensus of second-order agents with multiple time-varying delays[J]. Automatica, 2010, 46: 1994–1999. DOI:10.1016/j.automatica.2010.08.003 |
| [7] | Tahbaz-Salehi A, Jadbabaie A. Consensus over ergodic stationary graph processes[J]. IEEE Transactions on Automatic Control, 2010, 55(1): 225–230. DOI:10.1109/TAC.2009.2034054 |
| [8] |
明平松, 刘建昌.
随机多智能体系统一致稳定性分析[J]. 控制与决策, 2016, 31(3): 385–393.
Ming P S, Liu J C. Consensus stability analysis of stochastic multi-agent systems[J]. Control and Decision, 2016, 31(3): 385–393. |
| [9] | Zhang Q, Zhang J F. Distributed parameter estimation over unreliable networks with Markovian switching topologies[J]. IEEE Transactions on Automatic Control, 2012, 57(10): 2545–2560. DOI:10.1109/TAC.2012.2188353 |
| [10] | Zhao H. Leader-following consensus of data-sampled multi-agent systems with stochastic switching topologies[J]. Neurocomputing, 2015, 167: 172–178. DOI:10.1016/j.neucom.2015.04.080 |
| [11] | Dai J, Guo G. Event-based consensus for second-order multi-agent systems with actuator saturation under fixed and Markovian switching topologies[J]. Journal of the Franklin Institute, 2017, 354(14): 6098–6118. DOI:10.1016/j.jfranklin.2017.07.011 |
| [12] | Ming P, Liu J, Tan S, et al. Consensus stabilization of stochastic multi-agent system with Markovian switching topologies and stochastic communication noise[J]. Journal of the Franklin Institute, 2015, 352(9): 3684–3700. DOI:10.1016/j.jfranklin.2015.03.015 |
| [13] | Wang Z Q, Liu X X. Nonlinear internal model control for bearingless induction motor based on neural network inversion[J]. Acta Automatica Sinica, 2013, 39(4): 433–439. DOI:10.1016/S1874-1029(13)60043-9 |
| [14] | Ronch A D, Badcock K J, Wang Y, et al. Nonlinear model reduction for flexible aircraft control design[J]. International Journal of Modelling Identification&Control, 2012(2): 113–124. |
| [15] | Yan R, Dong Z Y, Saha T K, et al. A power system nonlinear adaptive decentralized controller design[J]. Automatica, 2010, 46(2): 330–336. DOI:10.1016/j.automatica.2009.10.020 |
| [16] | Tang Y. Output consensus of nonlinear multi-agent systems with unknown control directions[J]. Kybernetika, 2015, 51(2): 335–346. |
| [17] |
张振华, 彭世国.
时延多智能体系统领导跟随一致性研究[J]. 计算机应用研究, 2019, 36(2): 420–424.
Zhang Z H, Peng S G. Research on leader-following consensus of multi-agent systems with time delays[J]. Application Research of Computer, 2019, 36(2): 420–424. |
| [18] | Yu W, Chen G, Cao M, et al. Second-order consensus for multiagent systems with directed topologies and nonlinear dynamics[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2010, 40(3): 881–891. DOI:10.1109/TSMCB.2009.2031624 |
| [19] | Wang X H, Ji H B. Leader-follower consensus for a class of nonlinear multi-agent systems[J]. International Journal of Control Automation&Systems, 2012, 10(1): 27–35. DOI:10.1007/s12555-012-0104-3 |
| [20] | Gao L, Zhao G, Li G, et al. Allocating minimum number of leaders for seeking consensus over directed networks with time-varying nonlinear multi-agents[J]. International Journal of Control Automation and Systems, 2019, 17(1): 57–68. DOI:10.1007/s12555-018-0057-2 |
| [21] | Liu W, Huang J. Adaptive leader-following consensus for a class of higher-order nonlinear multi-agent systems with directed switching networks[J]. Automatica, 2017, 79: 84–92. DOI:10.1016/j.automatica.2017.02.010 |
| [22] |
唐朝君.
基于自适应控制的非线性多智能体系统一致性[J]. 重庆理工大学学报(自然科学版), 2019, 33(11): 137–142.
Tang Z J. Adaptive consensus for nonlinear multi-agent systems[J]. Journal of Chongqing University of Technology (Natural Science), 2019, 33(11): 137–142. |
| [23] | He P, Li Y, Park J H. Noise tolerance leader-following of high-order nonlinear dynamical multi-agent systems with switching topology and communication delay[J]. Journal of the Franklin Institute, 2016, 353(1): 108–143. DOI:10.1016/j.jfranklin.2015.10.013 |
| [24] | Bing C, Zhao C, Ma T, et al. Leaderless and leader-following consensus of multi-agent chaotic systems with unknown time delays and switching topologies[J]. Nonlinear Analysis Hybrid Systems, 2017, 24: 115–131. DOI:10.1016/j.nahs.2016.11.007 |
| [25] | Wen G, Duan Z, Chen G, et al. Consensus tracking of multi-agent systems with Lipschitz-type node dynamics and switching topologies[J]. IEEE Transactions on Circuits&Systems I-Regular Papers, 2014, 61(2): 499–511. |
| [26] | Yan Z P, Liu Y B, Zhou J J, et al. Consensus of multiple autonomous underwater vehicles with double independent Markovian switching topologies and timevarying delays[J]. Chinese Physics B, 2017, 26(4): 75–86. |
| [27] | Zhang X, Liu L, Feng G. Leader-follower consensus of time-varying nonlinear multi-agent systems[J]. Automatica, 2015, 52: 8–14. DOI:10.1016/j.automatica.2014.10.127 |
| [28] | Chu Y J, Liu T H. On the shortest arborescence of a directed graph[J]. Scientia Sinica, 1965, 14: 1396–1400. |



