2. 数字社区教育部工程研究中心, 北京 100124;
3. 城市轨道交通北京实验室, 北京 100124
2. Engineering Research Center of Digital Community, Ministry of Education, Beijing 100124, China;
3. Beijing Laboratory for Urban Mass Transit, Beijing 100124, China
0 引言
现实世界的大多数优化问题具有非线性约束、维度高、非强凸等特点,使用传统的数值解法难以获得满意的效果[1]。群智能优化算法主要模仿了自然界生物的聚集、觅食等行为,如粒子群算法(particle swarm algorithm,PSO)[2]、鲸鱼优化算法(whale optimization algorithm,WOA)[3]、灰狼优化算法(grey wolf optimization,GWO)[4]、鸽群优化算法(pigeon inspired optimization,PIO)[5]等,这类优化算法的原理相对简单、灵活性强,在解决大规模、非线性组合优化问题上具有计算成本低、精度高等优势[6],因此受到了众多学者的关注。
海鸥优化算法(seagull optimization algorithm,SOA)是2019年由Dhiman与Kumar提出的一种新型群智能优化算法[7],与粒子群(PSO)算法、遗传算法(genetic algorithm,GA)[8]、差分进化(differential evolution,DE)算法[9]等相比,SOA算法易于实现、参数简单,能够较好地解决压力容器设计[7]、可再生能源系统设计[10]、石油污染图像分割[11]等具有挑战性的大规模约束优化问题。虽然SOA算法具有一定的优势,但也存在收敛速度慢、容易陷入局部最优等不足,因此出现了一些改进方法,比如,通过莱维飞行产生具有重尾分布的随机游走来增加海鸥位置变化的多样性,从而加快算法的收敛速度[12];为了改善算法易陷入局部最优的问题,采用热交换公式替换SOA算法的螺旋攻击,使算法的局部搜索能力得以提升,降低了陷入局部最优的概率[13];文[14]则从全局寻优角度出发,将SOA算法的螺旋攻击与鲸鱼优化算法(WOA)的收缩包围相结合,并用征逃策略增强了SOA算法的全局寻优能力。从这些改进措施来看,虽然SOA算法性能有了一定程度的提升,但全局与局部搜索的协调能力有待加强。另外,局部搜索方式比较单一,缺乏灵活性,导致优化性能减弱。因此,如何提高SOA算法的寻优能力值得进一步研究。
基于上述,本文从平衡全局与局部搜索能力出发,设计了3种提高SOA算法寻优能力的改进策略。首先,改进非线性收敛因子与螺旋系数,平衡全局与局部搜索,避免最优解附近的振荡现象,以加快收敛速度;其次,通过增加海鸥的攻击方式,使用并行搜索提升局部寻优精度;最后,使用动态反向学习解决SOA算法易陷入局部最优的问题。通过实验证明了上述改进策略得到的改进海鸥优化算法(improved SOA,ISOA)在寻优能力上的优越性。
1 海鸥优化算法及其问题根据文[7]可知,海鸥优化算法(SOA)主要模拟了海鸥的两种自然行为,迁徙(全局搜索)与攻击(局部搜索)。迁徙即海鸥从现阶段不适宜生存的栖息地飞往适宜生存的地方,在迁徙的过程中海鸥会攻击海面上的猎物,算法具体描述及其问题分析如下所示。
1.1 迁徙海鸥的迁徙过程需要满足3个条件,即避免碰撞、确定移动方向和靠近最佳位置,从而以当前最佳海鸥的位置来指导其它海鸥进行位置更新。
1) 避免碰撞:通过附加变量产生不同的位置,避免海鸥在迁徙过程中相互发生碰撞,计算公式:
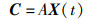
|
(1) |
其中,C表示海鸥个体与其它海鸥不发生碰撞时应处的位置;X(t)表示海鸥个体当前位置;t表示当前迭代次数;A表示附加变量,用于描述海鸥群体在搜索空间的移动行为,计算公式:
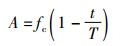
|
(2) |
其中,fc用来控制附加变量A的变化范围,fc一般取2;T表示最大迭代次数。
2) 确定移动方向:在避免碰撞的前提下,海鸥个体会根据当前最佳海鸥的位置来确定自己的移动方向,表达式为
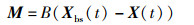
|
(3) |
其中,M表示海鸥个体与当前最佳海鸥的相对位置;Xbs(t)表示当前最佳海鸥的位置;B是协调全局与局部搜索的收敛因子:
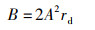
|
(4) |
其中,rd表示[0, 1]之间的随机数。
3) 靠近最佳位置:海鸥个体在确定了避免碰撞位置和移动方向后,向当前最佳海鸥的方向移动,表达式为
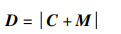
|
(5) |
其中,D表示海鸥个体与当前最佳海鸥的距离。
1.2 攻击海鸥攻击猎物的行为可以用xyz平面上的螺旋运动表示,具体描述为
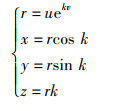
|
(6) |
其中,r表示海鸥的飞行半径;u、v是控制螺旋形状的系数,u、v一般均取1;k表示[0,2π]范围内的随机攻击角度;攻击猎物后的新位置为
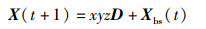
|
(7) |
从SOA算法的实现过程可以看出,虽然算法具有易于实现、参数简单的特点,但如下一些问题的存在限制了寻优性能的提升。
1) 收敛速度慢。式(4)中的非线性收敛因子B递减缓慢,使算法在全局搜索上比较费时。式(6)中的螺旋系数v为常数,导致算法后期因海鸥飞行半径r过大,在最优解附近振荡,无法快速收敛。
2) 搜索方式单一。由式(1)、式(2)知,同代海鸥个体以相同的附加变量A来控制避免碰撞位置C的产生。由于算法后期海鸥个体的位置X(t)比较接近,所以C非常相似,很难避免碰撞。另外,SOA算法仅有式(6)一种螺旋攻击方式,海鸥个体只能选择一个攻击角度,导致寻优精度降低。
3) 易陷入局部最优。由于群智能优化算法在搜索的过程的中会不可避免地陷入局部最优[15],而SOA算法中并未涉及跳出局部最优的措施,使其难以逃脱局部极值的束缚。
2 改进海鸥优化算法与收敛性分析基于上述关于SOA算法的问题描述,本节给出了3种改进策略,分别是:非线性收敛因子与螺旋系数的改进以加快收敛速度、并行搜索的加入以改善求解精度、动态反向学习的引入以避免陷入局部最优,从而得到一种改进海鸥优化算法(ISOA),本节最后介绍了ISOA算法的收敛性及步骤。
2.1 非线性收敛因子与螺旋系数在SOA算法的迭代过程中,从式(4)可以看出,非线性收敛因子B为[0,2A2]上的随机数,负责平衡算法的全局与局部搜索,结合式(2)可知,B的上界2A2随着附加变量A非线性递减至0。由于上界2A2递减速度较为缓慢,导致B偏大,无法快速缩短海鸥个体与当前最佳海鸥的距离,使算法在全局搜索上比较费时。为加快全局搜索,采用正切与反正切函数对非线性收敛因子B进行改进:
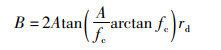
|
(8) |
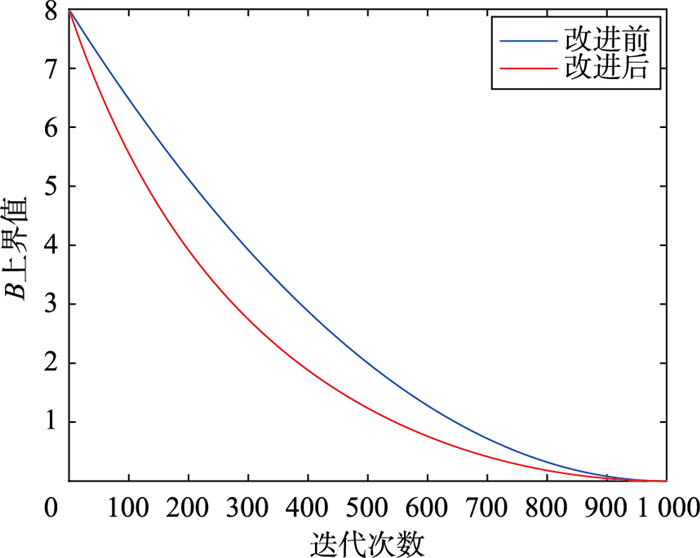
为保证改进前后B上界的起点与终点保持不变,式(8)中的参数A、fc取值不变。从图 1可知,改进后的B上界递减较快,使B相对较小,以此提升算法的全局搜索速度。
|
| 图 1 改进前后B上界变化对比图 Fig.1 Comparison of changes in the upper bound of B before and after the improvement |
由于式(6)中的螺旋系数v为常数(v=1),不能随着迭代过程自适应调整,使海鸥后期飞行半径过大,导致算法在最优解附近振荡,无法快速收敛。因此,本文采用余弦函数对v进行改进:
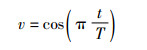
|
(9) |
改进后的螺旋系数v随着迭代过程的进行从1非线性降为-1,使海鸥前期的飞行半径较大,以探索最优解的大致位置,后期的飞行半径较小,以快速获得最优解的精确位置。
2.2 并行搜索为进一步避免海鸥在迁徙的过程中发生相互碰撞,将式(1)中的附加变量A乘以[0, 1]上的随机数,使同代海鸥个体以不同的附加变量来产生避免碰撞的位置C,改进后的式(1)为
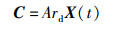
|
(10) |
由于SOA算法中海鸥的攻击行为(局部搜索)比较单一,导致算法局部寻优能力减弱。受到文[14] 将SOA算法的螺旋攻击与WOA算法的收缩包围相结合,通过增加海鸥攻击行为的多样性来提升算法寻优能力的启发,本文在式(7)的基础上分解出两种子攻击行为,使种群中适应度较大的个体可以进行多样搜索,以获得更好的攻击位置,子攻击行为为
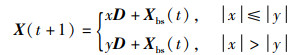
|
(11) |
另外,在SOA算法中海鸥个体只能随机选择一个攻击角度,没有对比参照,比较盲目,在一定程度上降低了算法的求解精度。因此,将式(6)中的海鸥攻击角度k进行扩展并记为k*。为保证攻击范围的合理性,k与k*在[0,2π]上互补。据此思想,得到海鸥以角度k*攻击猎物时在xyz平面的螺旋运动:
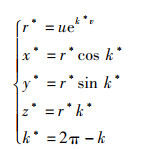
|
(12) |
其中,r*表示海鸥以角度k*攻击时的飞行半径,攻击后的新位置记为X*(t+1):
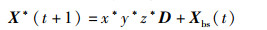
|
(13) |
根据式(12)和式(13),式(11)对应的两种子攻击行为由式(14)进行描述:
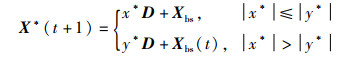
|
(14) |
当海鸥个体以角度k与k*完成并行攻击后,分别对新位置X(t+1)、X*(t+1)进行评价对比,并保留较优的位置。
2.3 动态反向学习反向学习是Tizhoosh于2005年提出的一种智能计算方法[16],主要分为一般反向学习与动态反向学习。当算法陷入局部最优时,通过反向学习生成反向解,可以帮助算法快速跳出局部最优,从而提高全局寻优精度[17]。与一般反向学习相比,动态反向学习能够自动调整反向搜索空间范围,具有自适应性。因此,将动态反向学习引入到SOA算法中,通过动态反向学习生成海鸥个体当前位置X(t)的反向位置X′(t),以扩大改海鸥搜索的有效范围,同时计算并选择X(t)与X′(t)中较优的位置(本文指适应度较小的个体所处的位置)进入下一次迭代,避免算法陷入局部最优。引入动态反向学习对X(t)进行更新的数学描述:
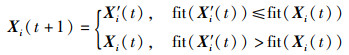
|
(15) |
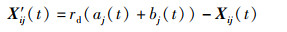
|
(16) |
其中,i=1,2,…,N;j=1,2,…,D;N表示种群规模;D表示搜索维度;Xi(t)与Xi(t+1)分别表示第t次与t+1次迭代时,种群中第i只海鸥的当前位置;X′ i(t)表示Xi(t)对应的反向位置;fit(·)表示适应度函数;Xij(t)与X′ ij(t)分别表示Xi(t)与X′ i(t)在第j维上的分量;aj(t)与bj(t)分别表示X(t)在第j维上的最大值与最小值。
从上述可知,通过非线性收敛因子与螺旋系数的改进、并行搜索的加入和动态反向学习的引入,从而得到一种改进海鸥优化算法(ISOA)。
2.4 ISOA算法收敛性分析文[18]使用马尔可夫过程分析过随机搜索算法的收敛性,由于ISOA算法的求解过程是一种随机搜索,因此采用马尔可夫过程分析ISOA算法的收敛性。首先证明ISOA算法的求解过程为有限齐次马尔可夫链,然后证明ISOA算法以概率1收敛于全局最优解。
假设待求解问题的目标状态空间S是有限集,参考文[18]可进行如下定义:
定义1 海鸥的状态集合由海鸥的位置构成,记为X(t)。ISOA算法在第t次迭代时,X(t)={xt,1,xt,2,,…,xt,N},x与S分别表示第t次迭代时算法的可行解与解空间,x∈S。{X(t),t≥0}构成一个离散的随机过程,令其状态空间为E。
定义2 待求解问题的全局最优集合为Cbs= 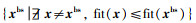
定义3 若对于任意的初始状态X0均有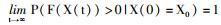
定理1 ISOA算法的寻优求解过程{X(t),t≥0} 为有限齐次马尔可夫链。
证明 因为目标状态空间S有限,种群规模N有限,所以状态空间E有限。当t=0时,海鸥的初始状态X(0)={x0,1,x0,2,…,x0,N}在整个搜索空间上随机生成,随着ISOA算法迭代求解的进行,海鸥的状态会被更新。令第t代的状态为X(t),则t+1代的状态为X(t+1)。因为式(6)与式(12)中的攻击角度k与k*、式(8)中的收敛因子B以及式(10) 中的避免碰撞位置C均为有限范围内的随机数,由式(7)、式(11)、式(13)、式(14)可知,X(t+1)的状态仅与X(t)的状态有关,与t无关,所以ISOA算法的寻优求解过程为有限齐次马尔可夫链。
定理2 状态空间E中包含最优解的个数单调不减,即对∀t≥0,m≥0,有:
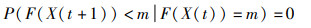
|
(17) |
证明 ISOA算法始终以当前最佳海鸥的位置来指导其它海鸥进行位置更新,而第t+1次迭代时用于指导的最佳海鸥来源于第t次的迭代求解,所以当第t代的最优解个数为m时,第t+1代的最优解个数不会小于m。
定理3 ISOA算法在任意的代数都有可能发现全局最优解,即对∀t≥0,有:
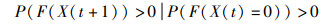
|
(18) |
证明 由于海鸥的初始状态X(0)是在整个搜索空间上随机生成的,其包含全局最优解的概率不为0,而ISOA算法搜索到任一可行解的概率也不为0,则在任意的代数发现全局最优解的概率不为0,因此ISOA算法在任意的代数都有可能发现全局最优解。
定理4 ISOA算法以概率1收敛于全局最优解,即:
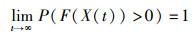
|
(19) |
证明 根据文[18]可知,在满足定理1~定理3的前提下,ISOA算法以概率1收敛于全局最优解。
2.5 ISOA算法步骤改进海鸥优化算法(ISOA)的求解步骤为:
Step 1 参数初始化。设置种群规模N,最大迭代次数T,搜索维度D,螺旋系数u以及控制系数fc。
Step 2 在整个搜索空间上随机生成N只海鸥的位置,分别计算海鸥个体的适应度与种群的平均适应度,并记录当前最佳海鸥的位置。
Step 3 根据式(2)、式(8)、式(9)分别计算附加变量A、非线性收敛因子B、螺旋系数v。
Step 4 迁徙(全局搜索)。根据式(10)、式(3)、式(5)迁徙飞行。
Step 5 攻击(局部搜索)。1) 以角度k进行攻击时,根据式(6)描述海鸥在xyz平面上的螺旋运动,若海鸥个体的适应度大于种群的平均适应度,则根据式(11)进行攻击;否则,根据式(7)进行攻击。2) 以角度k*进行攻击时,根据式(12)描述海鸥在xyz平面上的螺旋运动,若海鸥个体的适应度大于种群的平均适应度,则根据式(14)进行攻击;否则,根据式(13)进行攻击。攻击完成后,对新位置X(t+1)、X*(t+1)进行评价对比,并保留较优的位置。
Step 6 根据式(15)、式(16)进行动态反向学习,重新计算海鸥个体的适应度与种群的平均适应度,并更新当前最佳海鸥的位置。
Step 7 若达到最大迭代次数T,则输出当前最佳海鸥的位置,算法结束;否则,返回Step 3。
3 实验及结果分析为验证ISOA算法的优越性,选择求解函数全局最小值和PID控制器参数优化进行实验测试。实验在Matlab R2018b环境下编程实现,所用计算机CPU为Intel®CoreTMi5-9500CPU@3. 00 GHZ,内存为8 GB,系统为Win 10 64位。
3.1 求解函数全局最小值将2. 1节改进的算法记为SOA1,2. 1节和2. 2节共同改进的算法记为SOA2。选取16个基准测试函数将ISOA算法与SOA算法、SOA1算法、SOA2算法、鲸鱼优化算法(WOA)、粒子群(PSO)算法、差分进化(DE)算法、鸽群优化(PIO)算法、灰狼优化(GWO)算法进行对比实验。算法的关键参数按照文[7]设置(如表 1所示)。测试函数的名称、维度、定义域、全局最小值如表 2所示,其中f1~f8为高维单峰函数,f9~f12为高维多峰函数,f13~f16为低维多峰函数。为保证实验结果的合理性,每种算法的种群规模N=30,最大迭代次数T=1 000,独立运行50次。最后统计每种算法所求的函数最小值的平均值与标准差,并采用显著性水平为0. 05的Wilcoxon秩和检验对优化结果进行统计分析,详细结果如表 3所示,加黑字体表示最优值。
| 算法名称 | 参数 | 值 |
| SOA | 控制系数fc | 2 |
| 螺旋系数u、v | 1 | |
| WOA | 控制系数a | 2 |
| 选择概率p | 0.5 | |
| PSO | 惯性系数w | 0.75 |
| 认知系数与社会系数 | 1.8、2 | |
| DE | 交叉率 | 0.9 |
| 尺度因子 | 0.5 | |
| PIO | 指南因子R | 0.3 |
| GWO | 控制系数a | 2 |
| ISOA | 控制系数fc、螺旋系数u | 与SOA一致 |
| 函数名称 | 维度 | 定义域 | 最小值 |
| f1:Sphere | 30 | [-100, 100] | 0 |
| f2:Zakharov | 30 | [-5, 10] | 0 |
| f3:Schwefel 2.22 | 30 | [-10, 10] | 0 |
| f4:Quartic | 30 | [-1.28,1.28] | 0 |
| f5:Dixon-Price | 30 | [-10, 10] | 0 |
| f6:Schwefel 2.21 | 30 | [-10, 10] | 0 |
| f7:Sum Squares | 30 | [-10, 10] | 0 |
| f8:Rotated Hyper-Ellipsoid | 30 | [-65, 65] | 0 |
| f9:Ackley | 30 | [-32, 32] | 0 |
| f10:Alpine | 30 | [-10, 10] | 0 |
| f11:Griewank | 30 | [-600, 600] | 0 |
| f12:Rastrigin | 30 | [-5.12,5.12] | 0 |
| f13:Schaffer N.2 | 2 | [-100, 100] | 0 |
| f14:Holder Table | 2 | [-10, 10] | -19.208 5 |
| f15:Bukin N.6 | 2 | [-15, 15] | 0 |
| f16:Drop-Wave | 2 | [-5.12,5.12] | -1 |
| 对比项 | ISOA | SOA2 | SOA1 | SOA | WOA | PSO | DE | PIO | GWO | |
| 函数 | 指标 | |||||||||
| f1 | 平均值 | 0 | 6.45×10-188 | 9.29×10-38 | 5.05×10-2 | 3.10×10-12 | 3.50×100 | 2.05×10-1 | 7.44×100 | 2.30×10-58 |
| 标准差 | 0 | 0 | 6.26×10-37 | 1.83×10-1 | 2.12×10-11 | 5.68×103 | 8.00×10-1 | 1.04×101 | 1.12×10-57 | |
| f2 | 平均值 | 8.25×10-275 | 1.69×102 | 2.26×102 | 3.75×102 | 4.38×102 | 2.29×101 | 9.53×100 | 1.79×101 | 6.63×10-18 |
| 标准差 | 0 | 1.27×102 | 1.49×102 | 1.79×102 | 1.64×102 | 9.56×100 | 5.99×100 | 2.28×101 | 1.48×10-17 | |
| f3 | 平均值 | 0 | 1.76×10-115 | 1.32×10-25 | 7.00×10-3 | 3.85×10-8 | 1.36×101 | 7.40×10-3 | 2.03×100 | 1.05×10-34 |
| 标准差 | 0 | 1.25×10-114 | 7.95×10-25 | 1.03×10-2 | 2.30×10-7 | 4.28×100 | 1.36×10-2 | 1.87×100 | 1.22×10-34 | |
| f4 | 平均值 | 2.30×10-3 | 3.07×10-3 | 3.30×10-3 | 4.18×10-2 | 3.40×10-3 | 2.85×10-1 | 1.62×10-1 | 1.75×10-1 | 9.17×10-3 |
| 标准差 | 4.05×10-3 | 5.28×10-3 | 7.40×10-3 | 6.18×10-2 | 4.10×10-3 | 2.14×10-1 | 7.60×10-2 | 1.75×10-1 | 4.93×10-3 | |
| f5 | 平均值 | 1.25×10-7 | 1.32×10-1 | 6.42×10-1 | 6.82×10-1 | 7.34×10-2 | 2.76×102 | 3.06×100 | 5.40×100 | 4.04×10-6 |
| 标准差 | 1.73×10-7 | 2.59×10-1 | 4.39×10-1 | 3.87×10-1 | 2.12×10-1 | 2.25×102 | 4.40×100 | 6.42×100 | 3.48×10-6 | |
| f6 | 平均值 | 1.06×10-220 | 5.02×10-1 | 5.98×10-1 | 1.38×100 | 2.40×10-3 | 2.21×100 | 3.02×100 | 1.38×10-1 | 2.42×10-15 |
| 标准差 | 0 | 7.77×10-1 | 8.04×10-1 | 1.33×100 | 1.35×10-2 | 4.61×10-1 | 7.74×10-1 | 1.26×10-1 | 4.66×10-15 | |
| f7 | 平均值 | 0 | 1.05×10-193 | 8.00×10-39 | 5.60×10-3 | 3.29×10-13 | 4.94×101 | 1.14×10-1 | 5.11×100 | 1.65×10-59 |
| 标准差 | 0 | 0 | 5.66×10-38 | 1.70×10-2 | 2.04×10-12 | 1.96×101 | 7.55×10-1 | 8.88×100 | 5.87×10-59 | |
| f8 | 平均值 | 0 | 3.49×10-188 | 9.62×10-35 | 3.48×10-2 | 1.23×10-10 | 8.34×101 | 3.30×10-1 | 5.56×101 | 4.07×10-58 |
| 标准差 | 0 | 0 | 1.36×10-35 | 1.06×10-1 | 7.81×10-10 | 5.56×101 | 1.52×100 | 8.53×101 | 8.92×10-58 | |
| f9 | 平均值 | 2.31×10-15 | 2.52×10-15 | 3.09×10-15 | 1.17×10-2 | 1.24×10-6 | 6.90×100 | 9.75×10-1 | 1.52×100 | 1.58×10-14 |
| 标准差 | 2.15×10-15 | 2.29×10-15 | 2.86×10-15 | 1.58×10-2 | 5.50×10-3 | 1.30×100 | 1.05×100 | 1.11×100 | 2.38×10-15 | |
| f10 | 平均值 | 0 | 1.28×10-118 | 2.02×10-26 | 8.32×10-2 | 1.63×10-2 | 9.95×100 | 2.40×10-2 | 5.72×10-1 | 1.14×10-4 |
| 标准差 | 0 | 9.08×10-118 | 1.31×10-25 | 3.61×10-1 | 8.54×10-2 | 2.85×100 | 7.48×10-2 | 8.22×10-1 | 2.92×10-4 | |
| f11 | 平均值 | 0 | 2.91×10-191 | 8.36×10-40 | 1.45×10-4 | 5.50×10-14 | 1.10×10-3 | 5.00×10-4 | 3.15×10-2 | 2.07×10-60 |
| 标准差 | 0 | 0 | 5.64×10-39 | 5.51×10-4 | 2.77×10-13 | 6.29×10-4 | 1.90×10-3 | 5.78×10-2 | 1.01×10-59 | |
| f12 | 平均值 | 0 | 0 | 1.14×10-15 | 1.20×100 | 2.72×100 | 1.04×102 | 3.51×101 | 2.12×101 | 4.13×10-1 |
| 标准差 | 0 | 0 | 8.04×10-15 | 4.01×100 | 9.89×100 | 2.16×101 | 1.26×101 | 2.74×101 | 1.36×100 | |
| f13 | 平均值 | 0 | 5.62×10-4 | 6.25×10-4 | 7.10×10-3 | 3.30×10-3 | 4.50×10-3 | 4.90×10-3 | 1.50×10-3 | 3.70×10-3 |
| 标准差 | 0 | 1.40×10-3 | 1.30×10-3 | 1.02×10-2 | 4.60×10-3 | 4.20×10-3 | 3.20×10-3 | 2.30×10-3 | 4.80×10-3 | |
| f14 | 平均值 | -19.208 1 | -19.206 5 | -19.200 1 | -19.173 5 | -19.208 5 | -19.208 5 | -19.208 5 | -19.207 4 | -19.208 5 |
| 标准差 | 1.80×10-3 | 1.27×10-2 | 1.16×10-2 | 4.38×10-2 | 9.84×10-16 | 3.15×10-5 | 8.79×10-15 | 1.50×10-3 | 1.48×10-5 | |
| f15 | 平均值 | 1.04×10-1 | 1.23×10-1 | 1.86×10-1 | 7.58×10-1 | 9.37×10-2 | 1.05×10-1 | 8.64×10-2 | 7.50×10-1 | 1.93×10-1 |
| 标准差 | 4.37×10-2 | 7.19×10-2 | 6.45×10-2 | 1.33×100 | 7.39×10-2 | 5.97×10-2 | 6.42×10-2 | 3.33×10-1 | 1.21×10-1 | |
| f16 | 平均值 | -1 | -1 | -9.99×10-1 | -9.81×10-1 | -9.83×10-1 | -9.99×10-1 | -9.87×10-1 | -9.95×10-1 | -9.93×10-1 |
| 标准差 | 0 | 0 | 1.75×10-2 | 2.95×10-2 | 2.82×10-2 | 9.00×10-3 | 2.58×10-2 | 1.02×10-2 | 7.90×10-3 | |
| ISOA> | 14 | 16 | 16 | 14 | 15 | 14 | 16 | 15 | ||
| ISOA= | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| ISOA < | 0 | 0 | 0 | 2 | 1 | 2 | 0 | 1 | ||
| 注:ISOA>:ISOA明显优于对比算法的函数个数;ISOA=:ISOA与对比算法无明显差异的函数个数;ISOA < :ISOA明显差于对比算法的函数个数。 | ||||||||||
对比表 3所列数据,由于同代海鸥个体使用不同的附加变量A来产生避免碰撞的位置C,达到了避免相互碰撞的目标,并行搜索的加入提升了海鸥攻击行为的多样性,动态反向学习的引入,使算法突破了局部极值的束缚,从而在单峰函数f1~f3、f7、f8,多峰函数f10~f13、f16的实验数值上表现为:ISOA算法具有较高的求解精度且优化结果稳定。虽然在函数f14上,ISOA算法的优化结果上略逊于WOA算法,但比SOA、SOA1、SOA2算法要好。另外,在函数f15上,ISOA算法求解的平均值虽然比DE算法差,但比其余8种算法好,且标准差是9种算法中最小的。
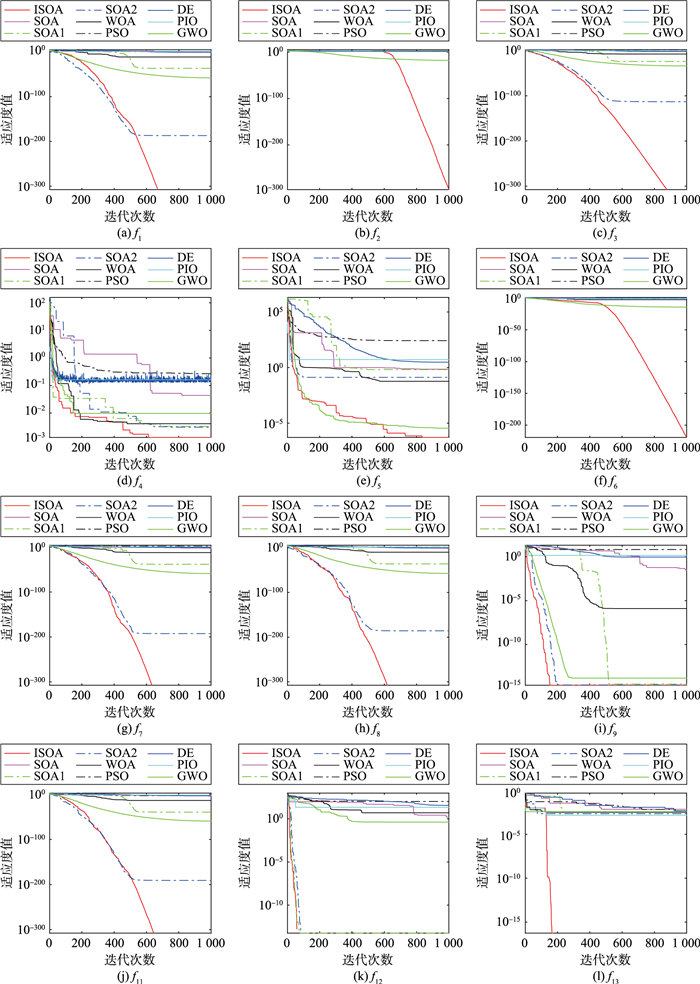
图 2给出了部分基准测试函数的收敛速度曲线。从图 2可以看出,由于改进后的非线性收敛因子B与螺旋系数v平衡了ISOA算法的全局与局部搜索,使其具有较快的收敛速度。另外,在迭代求解的过程中,当其它算法过早收敛,陷入局部最优时,ISOA算法通过动态反向学习可以快速地跳出局部最优,具有较强的全局搜索能力。
|
| 图 2 部分基准测试函数收敛速度曲线 Fig.2 Convergence speed curves of some benchmark test functions |
在工业过程控制中,大多采用闭环的PID控制策略[19]。对于复杂多变的实际系统,控制参数如何整定仍是有待解决的问题[20]。相比试凑法、Z-N法,将群智能优化算法用于PID的参数优化整定,可以有效提高控制器的性能,缩短调节时间[21]。下面采用ISOA算法、SOA算法以及Z-N法对工业中5种常见的对象模型在阶跃响应下的PID参数进行优化整定。被控对象的模型如下所示:
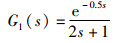
|
(20) |
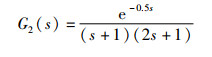
|
(21) |
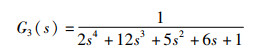
|
(22) |
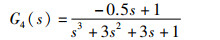
|
(23) |
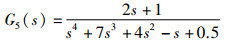
|
(24) |
其中,G1(s)、G2(s)为工业常用被控对象模型;G3(s)为复杂对象;G4(s)为具有反向特性的对象;G5(s)为不稳定对象。
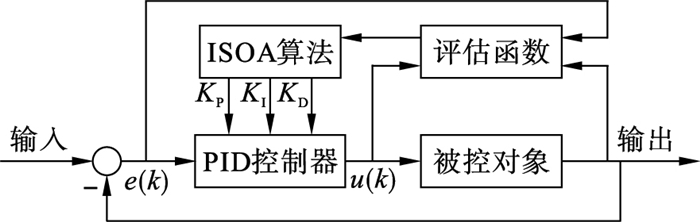
ISOA算法优化PID控制器的3个参数KP、KI、KD的原理如图 3所示,为使控制器获得良好的综合性能并避免超调,目标函数定义为
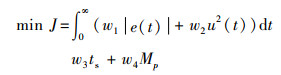
|
(25) |
|
| 图 3 ISOA算法优化PID控制器参数原理图 Fig.3 Schematic diagram of PID controller parameters optimized by ISOA algorithm |
其中,e(t)为控制偏差;u(t)为控制器输出;ts为调节时间(±2%标准);Mp为超调量;w1~w4为权值,且w4>>w1。
PID参数优化整定实验的相关参数设置为:最大迭代次数T=50,种群数量N=30,维度D=3,KP、KI、KD的优化区间分别为[0, 20]、[0, 20]、[0, 10],w1~w4分别取0. 99、0. 01、1、100,采样时间为0. 01 s。
由于ISOA算法与SOA算法的参数优化结果具有一定的随机性,为公平起见,分别对2种算法独立运行10次,并取各自的最优值。5种对象模型在阶跃信号下的PID参数优化结果及评价指标如表 4所示,其中tr表示上升时间,tp表示峰值时间,加黑为最优指标。
| 对象模型 | 整定方法 | KP | KI | KD | tr/s | tp/s | ts/s | Mp/% |
| G1(s) | ISOA | 12.651 | 6.389 | 0.215 | 0.36 | 0.63 | 0 | |
| SOA | 15.464 | 4.658 | 0.377 | 0.33 | 1.09 | 0 | ||
| Z-N | 3.785 | 3.616 | 0.120 | 0.86 | 1.93 | 3.66 | 6.80 | |
| G2(s) | ISOA | 3.230 | 0.945 | 0.702 | 1.43 | 2.83 | 6.99 | 3.5 |
| SOA | 3.994 | 0.693 | 0.130 | 1.21 | 2.34 | 12.85 | 7.2 | |
| Z-N | 2.184 | 1.184 | 0.233 | 1.60 | 3.62 | 8.02 | 17.7 | |
| G3(s) | ISOA | 0.322 | 0.151 | 0.327 | 1.11 | 2.46 | 3.52 | 7.4 |
| SOA | 0.306 | 0.160 | 0.442 | 1.07 | 2.40 | 3.58 | 8.6 | |
| Z-N | 0.480 | 0.182 | 0.379 | 1.04 | 2.50 | 3.96 | 8.7 | |
| G4(s) | ISOA | 1.005 | 0.410 | 0.672 | 2.74 | 6.20 | 4.93 | 0.6 |
| SOA | 0.924 | 0.435 | 0.735 | 2.85 | 7.50 | 10.42 | 4.4 | |
| Z-N | 0.952 | 0.533 | 0.575 | 2.30 | 5.84 | 12.95 | 16.8 | |
| G5(s) | ISOA | 6.073 | 0.389 | 10.00 | 2.19 | 5.25 | 7.96 | 4.3 |
| SOA | 4.379 | 0.338 | 9.746 | 2.92 | 6.75 | 10.92 | 5.1 | |
| Z-N | 5.739 | 1.395 | 8.264 | 1.75 | 4.80 | 14.15 | 28.2 |
对比表 4所列数据,模型G1(s)、G2(s)中,由ISOA算法与SOA算法整定的参数在4个评价指标上的表现均由优于Z-N法整定的参数,尤其在模型G1(s)中,ISOA算法不仅使系统的调节时间大为缩短且超调量为0。在模型G3(s)、G4(s)、G5(s)中,虽然优化算法整定的参数使系统在阶跃响应下的上升时间与峰值时间略长,但超调量变小、调节时间缩短。
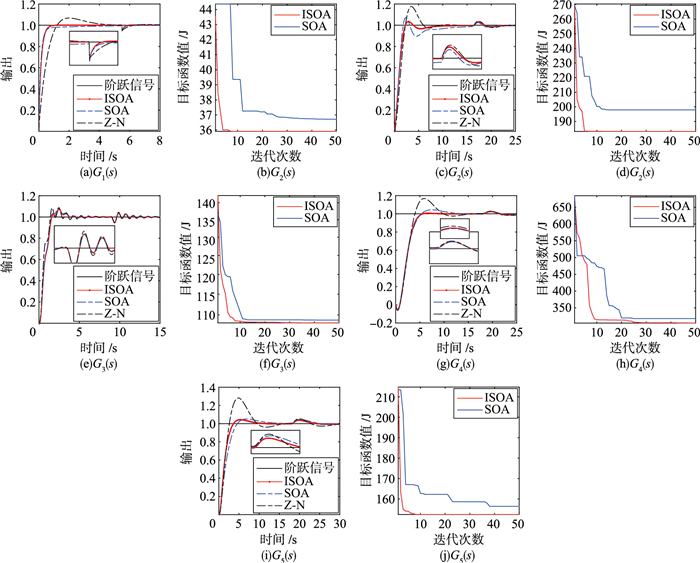
为进一步分析3种方法整定的PID参数效果,图 4给出了5种对象模型的阶跃响应输出与收敛曲线。从图 4可以看出,模型G1(s)、G4(s)、G5(s)中ISOA算法整定的参数使系统的上升过程较为平稳且回调小,即使有扰动存在,系统也能快速稳定。在模型G2(s)、G5(s)中,ISOA算法的收敛速度快于SOA算法且求解精度较高。在模型G3(s)中,由Z-N法整定的参数虽然使系统的上升速度略快但输出的波动幅度更大,波动时间更长。从以上求解函数全局最小值和PID控制器参数优化的实验结果可以看出,ISOA算法能有效处理低维或高维的函数极值求解问题,具有一定的普适性。另外,ISOA算法所优化的PID参数使控制器的性能得以提升,在一定程度上能够满足工业生产过程的控制需求。
|
| 图 4 5种对象模型阶跃响应输出与收敛曲线 Fig.4 Step response output and convergence curves of five object models |
为提高SOA算法的寻优能力,本文提出了3种改进策略,得到一种改进海鸥优化算法(ISOA),并证明了其全局收敛性。通过实验证明了改进策略的优越性。与现有的SOA算法相比,本文方法的主要贡献有:
1) 通过加快非线性收敛因子的递减速度,改善了算法全局与局部搜索的协调能力。同时,通过螺旋系数的自适应变化,避免了算法在最优解附近发生振荡。二者的改进加快了算法的收敛速度。
2) 并行搜索通过增加海鸥的攻击行为与攻击角度,提升了算法的局部寻优能力。
3) 动态反向学习的引入,扩大了海鸥搜索的有效范围,使算法可以快速跳出局部最优,进而优化了算法的全局搜索。
从实验结果中可以看出,ISOA算法在求解过程中不易陷入局部最优,具有较强的搜索能力,无论是在低维还是高维的约束优化问题上均表现出了较好的性能,从而在函数极值求解与参数优化领域具有一定的应用优势。
虽然本文提出的3种改进策略显著提升了SOA算法的寻优能力,但也增加了算法所需的计算资源,如何提高ISOA算法在工业过程参数优化领域的在线应用效果是下一步研究的重点。
| [1] |
Yan Z, Wang J, Li G C. A collective neurodynamic optimization approach to bound-constrained nonconvex optimization[J]. Neural Networks, 2014, 55(7): 20-29. |
| [2] |
Kennedy J, Eberhart R C. Particle swarm optimization[C]//IEEE International Conference on Neural Networks. Piscataway, USA: IEEE, 1995, 1942-1948.
|
| [3] |
Mirjalili S, Lewis A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95(5): 51-67. |
| [4] |
Mirjalili S, Mirjalili S M, Lewis A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69(3): 46-61. |
| [5] |
Duan H B, Qiao P X. Pigeon inspired optimization: A new swarm intelligence optimizer for air robot path planning[J]. International Journal of Intelligent Computing and Cybernetics, 2014, 7(1): 24-37. DOI:10.1108/IJICC-02-2014-0005 |
| [6] |
Kar A K. Bio inspired computing-A review of algorithms and scope of applications[J]. Expert Systems with Applications, 2016, 59(10): 20-32. |
| [7] |
Dhiman G, Kumar V. Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems[J]. Knowledge-Based Systems, 2019, 165(2): 169-196. |
| [8] |
Holland J H. Adaptation in natural and artificial system[M]. Ann Arbor, USA: University of Michigan Press, 1975: 211-247.
|
| [9] |
Storn R, Price K. Differential evolution-A simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359. DOI:10.1023/A:1008202821328 |
| [10] |
Lei G, Song H Q, Rodriguez D. Power generation cost minimization of the grid-connected hybrid renewable energy system through optimal sizing using the modified seagull optimization technique[J]. Energy Reports, 2020, 6(11): 3365-3376. |
| [11] |
Jia H M, Xing Z K, Song W L. Three dimensional pulse coupled neural network based on hybrid optimization algorithm for oil pollution image segmentation[J/OL]. Remote Sensing, 2019, 11(9). [2021-08-03]. http://www.mdpi.com/2072-4292/11/9/1046. DOI: 10.3390/rs11091046.
|
| [12] |
Cao Y, Li Y Q, Zhang G, et al. Experimental modeling of PEM fuel cells using a new improved seagull optimization algorithm[J]. Energy Reports, 2019, 5(11): 1616-1625. |
| [13] |
Jia H M, Xing Z K, Song W L. A new hybrid seagull optimization algorithm for feature selection[J]. IEEE Access, 2019, 7(4): 49614-49631. |
| [14] |
Che Y H, He D X. A hybrid whale optimization with seagull algorithm for global optimization problems[J]. Mathematical Problems in Engineering, 2021, 2021(4): 1-31. |
| [15] |
刘振, 鲁华杰, 刘文彪. 自适应协同进化蝙蝠算法[J]. 控制与决策, 2019, 34(8): 1626-1634. Liu Z, Lu H J, Liu W B. Adaptive cooperation evolutionary bat algorithm[J]. Control and Decision, 2019, 34(8): 1626-1634. |
| [16] |
Tizhoosh H R. Opposition-based learning: A new scheme for machine intelligence[C]//International Conference on Computational Intelligence for Modeling Control and Automation. Piscataway, USA: IEEE, 2005: 695-701.
|
| [17] |
张强, 刘丽杰. 一种动态分组多策略果蝇优化算法[J]. 信息与控制, 2018, 47(4): 479-485. Zhang Q, Liu L J. Dynamic grouping and multi-strategy fruit fly optimization algorithm[J]. Information and Control, 2018, 47(4): 479-485. |
| [18] |
李宝磊, 施心陵, 苟常兴, 等. 多元优化算法及其收敛性分析[J]. 自动化学报, 2015, 41(5): 949-959. Li B L, Shi X L, Gou C X, et al. Multivariant optimization algorithm and its convergence analysis[J]. Acta Automatica Sinica, 2015, 41(5): 949-959. |
| [19] |
王伟, 张晶涛, 柴天佑. PID参数先进整定方法综述[J]. 自动化学报, 2000, 26(3): 347-355. Wang W, Zhang J T, Chai T Y. A survey of advanced PID parameter tuning methods[J]. Acta Automatica Sinica, 2000, 26(3): 347-355. |
| [20] |
房美琦, 李醒飞, 姜明波, 等. 深海剖面浮标RBF-PID定深控制[J]. 信息与控制, 2019, 48(6): 641-648. Fang M Q, Li X F, Jiang M B, et al. RBF-PID depth control of deep-sea profiling floats[J]. Information and Control, 2019, 48(6): 641-648. |
| [21] |
靳其兵, 苏奇新. 基于改进布谷鸟算法的PID控制器整定新方法[J]. 信息与控制, 2018, 47(4): 505-512. Jin Q B, Su Q X. Novel modified CS algorithm-based PID-controller tuning method[J]. Information and Control, 2018, 47(4): 505-512. |



