0 引言
路径规划[1]是研究移动智能机器人的基础问题之一。路径规划是指智能机器人参考所获取的数据信息,自动规划出一条从初始点到终点且无碰撞的最短路径,这项研究获得国内外学者广泛的关注。常见的路径规划算法被分为经典算法和智能优化算法。
经典算法需要提前载入信息环境,如A*算法、人工势场算法等。A*算法在文[2]中被首次提出,基本思想是根据环境信息,计算到每个节点之间的代价,选择代价最小的的路径。但A*算法在复杂环境下会出现搜索失败的情况,就算搜索成功,其搜索效率也较低。王洪斌等[3]为提高A*算法搜索效率,将动态窗口法、自适应优化算法和步长调节算法融合到A*算法中。陈靖辉等[4]通过除去规划过程中的扩展节点,来提高算法的搜索效率。人工势场算法由Khatib[5]提出,该算法中目标和障碍物对机器人就像均匀电场中的电荷,存在排斥力和吸引力,吸引机器人向终点移动,排斥向障碍物移动。但该算法存在易陷入局部极值和障碍物附近目标点不可达等问题。欧阳鑫玉等[6]提出以人工势场为主,栅格为辅的方法,并增加障碍物的斥力函数,提高算法跳出局部最优解的能力。赵明等[7]对人工势场算法进行改进,提出了一种域势场,帮助机器人逃离局部极值,并加入引导势场,提高算法的搜索效率。
智能优化算法是根据实时测量的环境信息进行规划,如遗传算法、粒子群算法和灰狼算法等。刘洋等[8]针对传统遗传算法在路径规划的过程中解的质量欠佳的问题,提出在适应度函数中增加安全距离与自适应惩罚因子,并融合贝塞尔曲线,使其能够搜索到更短且更光滑的路径。魏彤等[9]在传统遗传算法中增加了插入和删除两种算子,并修改适应度函数,把连贯性作为适应度指标,所提方法能规划出更优路径且更为平稳。粒子群算法在实际应用中,易早熟。胡章芳等[10]对此问题,将粒子群算法和遗传算法相融合,使用交换和突变的操作,避免算法早熟。陈嘉林等[11]针对粒子群算法易早熟的现象,结合了初始化种群策略和惩罚函数提高算法的寻优能力,并根据当前粒子位置进行种群进化,从而摆脱算法早熟。灰狼算法[12]是于2014年提出的一种新型智能优化算法,在测试函数中,较粒子群、遗传等传统智能优化算法具有更好的求解精度,目前学者已将其应用于各个领域,其中包括路径规划研究。王永琦等[13]在灰狼算法的基础上采用反向学习方法,采用初始化灰狼种群,提升初始解的质量的方法,并借助精英反向学习策略,提高算法寻优能力。游达章等[14]对灰狼算法中的线性收敛因子进行改进,使之变为非线性,增强灰狼算法跳出局部最优值的能力。虽然这些算法在改进后一定程度上提高了路径的寻优效果,但测试地图较小且环境简单,很难说明算法具有解决复杂问题的能力,因此需要一种能应用于更加复杂地图的路径规划中的新算法。
经典算法在复杂环境下计算量大、计算时间长,很难完成实时路径更新,而智能优化算法能实时测量周围环境信息,计算速度快。因此,对于单个机器人路径规划问题,可考虑采用狮群优化算法[15]进行路径规划,并在环境较为复杂的地图进行测试。狮群优化算法是一种新型智能优化算法,目前已经应用于汽轮机热耗功率模型预测[16]、云计算资源调度策略优化[17]、车间调度[18]、极限学习机废水处理[19]、水电站优化调度[20]和二氧化碳排放预测[21]等领域中。基于已有的研究发现,狮群算法存在易陷入局部最优、寻优能力弱等问题,且现有的改进不适用于2维路径规划当中。因此,针对路径规划问题,本文提出改进狮群算法。首先,进行混沌初始化操作并引入调节因子ξ,增加算法的搜索效率,并减少不同时期不同行为幼狮数量几乎相同导致算法多样性不足的问题;其次,引入方向约束性函数,避免算法盲目搜索,加快算法的收敛精度;再次,提出一种双种群并行结构的狮群算法,通过交叉和变异操作,提高算法搜索能力;最后,通过实验仿真验证所提出算法的有效性,并融合四阶贝塞尔曲线对路径进行平滑处理[22],使路径更适合机器人移动。
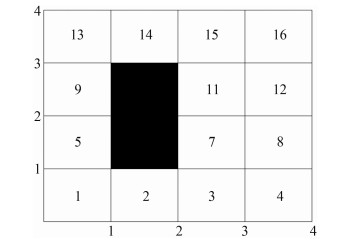
1 模型建立和路径平滑处理 1.1 模型建立在路径规划中,运用栅格法建立移动智能机器人的移动环境标准模型,将智能机器人看作是一个质点,活动空间为2维平面。如图 1以4×4大小的矩阵为例,白色区域为可行区域,即(x,y)=0;黑色区域为禁区,即(x,y)=1。以左下角开始,分别对栅格进行编号,分别为{1,2,3…,16}。栅格编号与坐标之间的关系可以表示为
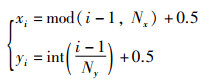
|
(1) |
|
| 图 1 栅格地图 Fig.1 Grid map |
式(1)中Nx和Ny分别表示栅格图中的第N行和第N列,mod为取余函数,int表示取整函数。
在算法中,适应度函数是问题的优化目标函数,适应度好坏代表解的优劣。一般情况下,适应度值越大,表示该解越好,就倾向选择该解。现假设算法搜索到一条新路径,将新路径的长度和旧路径长度进行对比,若新路径更短,即适应度值更大,则更新路径。因此,本文优化目标是机器人移动路径的长度,数学表达式为
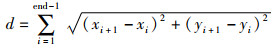
|
(2) |
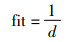
|
(3) |
式(2)表示机器人移动路径的长度,(xi,yi)表示当前节点坐标,(xi+1,yi+1)表示下一节点坐标,end表示终点坐标。式(3)表示适应度值,规划出的路径长度越长,则适应度值越低,反之,路径越短,适应值越高。
1.2 四阶贝塞尔曲线平滑处理在栅格地图中规划中路径转角大,会使智能机器人在运动中遇到急转弯,迫使移动机器人在停止、旋转和重启之间不断切换运动状态,这样不平稳的运动会导致机器人打滑,不仅增加路径长度,也使得机器人的功耗、零件磨损增加。特别是对一些特殊的机器人(如机器人轮椅、救援机器人),急转弯可能会导致意外事故。因此,研究中对智能机器人规划出的路径进行了平滑,采用伯恩斯坦多项式演变而来的四阶贝塞尔曲线,不仅可以满足移动机器人的运动学约束,而且可以减少路径行走的时间和功耗,提高机器人的运动效率。
平面贝塞尔曲线的定义为
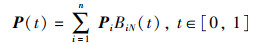
|
(4) |
其中,Pi为顶点坐标值;BiN(t)为伯恩斯坦多项式基函数:
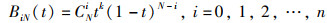
|
(5) |
由式(4)、式(5)可以推导得到四阶贝塞尔曲线方程:
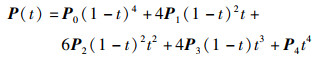
|
(6) |
当t∈(0,1)时,就能生成四次贝塞尔曲线。曲线上任意一点的曲率公式为
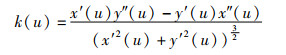
|
(7) |
其中,u表示曲线上任意一点的曲率。
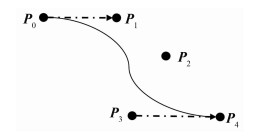
图 2为四阶贝塞尔曲线示例图,为防止平滑后的路径和障碍物发生碰撞,因此研究中只对机器人移动轨迹转角附近进行平滑处理。
|
| 图 2 四阶贝塞尔曲线示例图 Fig.2 Example graph of fourth-order Bezier curve |
图 2中P0(x0,y0)与P4(x4,y4)点的坐标值可以由算法所规划出的路径里得到,设P0与P1的距离为d1,可以得到P1(x1,d1),将P2=(x2,y2)代入曲率式(7)得到P2(4k(0)d12/3,y2),设P3与P4距离为d4,可以得到P3(x4-d4,y4-d4)。
满足曲率约束条件才能形成贝塞尔曲线[23]。若机器人转弯半径为R(本文R=3),最大曲率kmax=1/R,则最小曲率kmin=0,所以上下界约束条件表示为:kmin≤k(u)≤kmax。
每条四阶贝塞尔曲线由5个点构成,其中d1、d4、y2为变量,并且要满足曲率最大值和最小值之间的差值最小,所以,曲率优化目标函数为
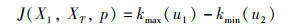
|
(8) |
式中,u1,u2∈[0, 1];目标函数中p代表参数d1、d4、y2。
生成若干条贝塞尔曲线后,要选择满足两点判断标准:
1) 路径上每个点,都与障碍物形成安全距离。
2) 若满足条件1),则比较所有路径的长短,选择最优路径,输出该路径作为结果。
2 改进狮群算法 2.1 基础狮群算法狮群算法是模拟狮群活动捕猎和繁殖一种新型智能优化算法。狮群具有严格的社会制度,每个狮群中包含狮王、母狮和幼狮,不同的狮子具有不同的行为方式和捕猎行为,其中狮王优先享有食物;母狮负责确认猎物位置,并捕猎;幼狮跟随学习,之后会被驱逐出狮群。
对于一个维度为D的全局优化问题f(X),设置迭代次数为T,设狮群的数量为N,每个狮子的位置代表所考虑问题的潜在解决方案,可以用一个D维向量表示:
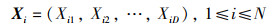
|
(9) |
狮王和母狮为成年狮,其占整个种群数量N的比例称为成年狮的比例因子,记作β∈(0,1)
首先,狮王是占有整个狮群最优位置的狮子,会优先享有猎物,在适应度值最大的附近进行小范围移动,并探寻猎物周围是否存在更好的解,其更新公式为
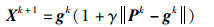
|
(10) |
式中,Xk+1代表狮王更新获得的下一代全局最佳位置,gk为当前迭代最佳位置,Pk代表狮王历史最佳位置,γ是[0, 1]范围内服从高斯分布随机数。
其次,母狮会确认猎物(解)的位置,向猎物发起攻击,通常会和另一只母狮合作。母狮位置更新公式为
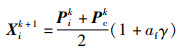
|
(11) |
式中,Pik是第i个狮子在经历第k次迭代后的历史最优位置,Pck是除了第i个狮子之外的另一个母狮的最优位置。af是扰动因子,是一种自适应的动态参数,会逐渐减小,af定义为
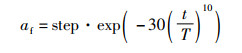
|
(12) |
其中,
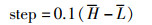
|
(13) |
式中,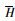
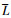
最后,幼狮在狩猎过程中可能会出现3种情况,见式(14)。当随机数q≤ 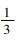
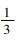
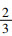
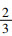
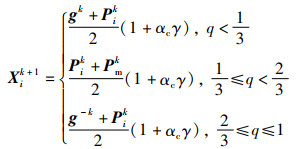
|
(14) |
式中,Pik代表幼狮历史最佳位置;Pmk为母狮的历史最佳位置;q为(0,1)范围内的随机数,g-k表示远离狮王的反向位置:
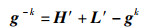
|
(15) |
其中,H′是解空间维度最远位置,L′是解空间维度平均位置。
同样的,幼狮的更新方程加入自适应的扰动因子ac,随迭代次数增加,步长逐渐缩小,避免后期大范围搜索:
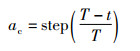
|
(16) |
混沌具有随机性和历遍性,当前在很多智能优化算法中都有应用,以提高算法初始解的质量。因此,个体应尽可能地遍历整个搜索空间,本文采用sin映射产生混沌序列用于种群初始化。目前已有学者证明[24]无限次折叠的Sin映射模型比有限次折叠的Logistic和Tent映射模型更具有混沌特性,其数学模型为
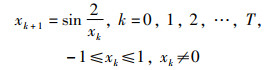
|
(17) |
Sin映射折叠次数为无限次,在分布区间[-1, 1]内有无穷个固定点和零点,所以该映射要形成混沌必须满足:
1) 初始值不能为0。
2) 初始值不可取固定点的数值。
2.2.2 策略2:引入调节因子ξLSO算法在局部搜索时,十分依赖母狮的协作捕猎,幼狮作为灵活度最高的个体,承担局部搜索和全局搜索的任务,幼狮的更新方式由整数q随机产生的,分布区间(0,1)被q平均分成3种行为方式,使得幼狮等概率执行3种行为方式,这使得不同行为模式的幼狮数量在算法的前中后期几乎相同,丧失了算法的多样性,易使算法早熟。为了协调算法前中后期,幼狮不同的行为,引入调节因子ξ,表示式(18):
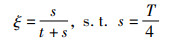
|
(18) |
因此,幼狮的位置更新公式,更新为
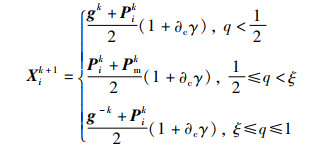
|
(19) |
这样在算法运算的前期,幼狮会优先跟随成年狮学习,提高搜索速度;运算后期,幼狮会被驱逐出狮群,进行随机游走,避免算法早熟,陷入局部极值。
2.2.3 策略3:引入方向约束性函数LSO算法中,母狮负责局部搜寻最优值,但是由于LSO算法没有指明狮群的移动方向,导致算法前期需要大量的搜索,降低了寻优的效率。为了加快收敛速度,本文提出了方向约束性函数cos θ:
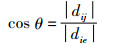
|
(20) |
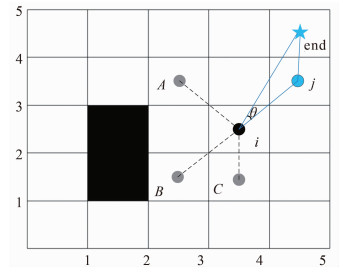
式中,dij表示当前点到目标点的距离,die表示目标点到终点的距离,i表示当前点,j表示下一点,e表示终点。图 3为方向约束性函数cos θ示意图。
|
| 图 3 cos θ示意图 Fig.3 cos θ schematic diagram |
ij两点与ie两点形成的夹角为θ,当下一节点j的选择靠近终点时,θ角度会小于90°,值为正;当下一节点j的选择远离终点时,如点A、点B、点C,θ角度大于90°,值为负,相较与A、B、C点,选择j点可以更快到达终点,可以简单理解为靠近最优解步伐加大,反之,远离最优解步伐减小。
重新设计的步长函数更新为
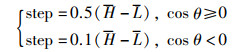
|
(21) |
当选择点j时,母狮的扰动因子增大,步长变大,使母狮更快向终点靠近。当选择A、B、C点时,母狮的扰动因子减小,步长变小,防止母狮远离终点。改进后使得算收敛精度提高,同时仍保持算法的随机性。在测试函数优化时,靠近最优解步长变大,反之。
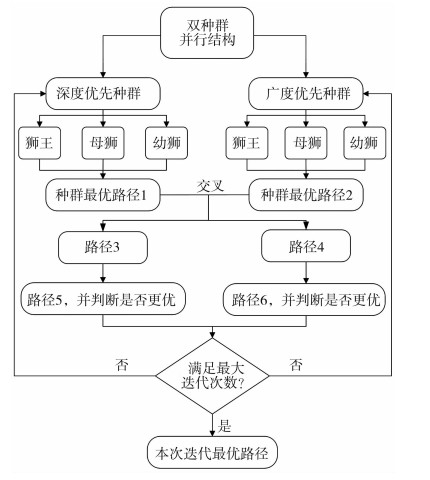
2.2.4 策略4:双种群并行结构根据赵燕伟[25]等提出的双种群遗传算法,提出了本文基于狮群的双种群平行结构,通过双种群来平衡算法的求解能力和搜索速度。算法运行开始会将种群一分为二,两个种群同时进行搜索,能减少算法的运行时间。图 4为双种群并行结构流程示意图。
|
| 图 4 双种群并行结构 Fig.4 Parallel structure of dual populations |
成年狮在整个群体中负责寻优和在最佳解附近搜索。由于狮王处于最佳位置不需要大范围的搜索,并在最优值附近小范围搜索,保证了算法的稳定性。幼狮会跟随狮王周围游动,也会跟随母狮学习,一部分幼狮也会远离狮王进行移动,防止陷入局部最优,保证了算法的随机性。因此在两个种群中,对不同狮群的比例进行调整,一个种群拥有较多的狮王,负责探索更高质量的解,另一个种群拥有较多的幼狮,使算法更具多样性,因此设置深度优先种群的成年狮比例因子β=0.3,广度种群的成年狮比例因子β=0.1。当两个种群搜索结束之后。借鉴遗传算法的方法,对得到的路径进行局部路径变异和部分路径的交换,产生的最优路径为此次迭代的结果。
使用遗传算法二进制编码对栅格进行编码,每条路径表示为一条基因序列(染色体)。p={p1,p2,…,pn}表示一条路径,其中pi=(1,2,3,…,n),为路径上第i个节点的栅格序号,p1、pn分别为起止序号。
双种群平行结构中广度种群和深度种群所生成第一代的两条最优路径作为遗传算法的父代个体,通过单点交叉的方式,组合成集合J,集合J由两个父代路径中相同的点所组成。去掉初始点和终点,若J非空,则随机挑选一个染色体编码,在父代中将选中染色体编码之后的路径展开单点交叉,反之则不交叉。例如,第一次形成的父代的个体依次为{1,5,9,14,15,11,7,8,12,15,16}和{1,2,3,4,7,8,12,16},除去起止点外共同点的集合为J={7,8,12},随机产生一个小于J集合点数量的整数R,此时R∈[1,3],如果R=1,那么交换节点J(R)之后的路径,得到子代分别为{1,5,9,14,15,11,7,8,12,16}和{1,2,3,4,7,8,15,16}。
交叉后进行变异操作。随机选择子代中两个非相邻栅格,首先删去起止点之间的路径,再分别从起止点进行路径规划,产生一新路径。若产生路径与原路径相同,则再次进行变异操作。例如,对于子代{1,5,9,14,15,11,7,8,12,16},变异操作后得到路径{1,6,9,15,12,7,8,12,16}。
比较两个种群得到的路径,判断交叉和变异后的子代是否更好:如果更好则保留子代,如果非更优则舍弃。最后,输出最优路径。
2.3 算法流程改进狮群算法的具体实行步骤:
Step 1:混沌初始化狮群。
Step 2:设置两个并行种群参数,β1=0.3,β2=0.1,D(xi)=50,Q=40,T=50。
Step 3:狮群角色状态的初始化。
Step 4:更新狮王、母狮及幼狮的位置。
Step 5:依据狮群中每个狮子的位置计算适应度值大小,更新每个狮子的最佳位置和历史最佳位置。
Step 6:对两个种群得到的解开展交叉和变异操作,变异几率pm=0.1。
Step 7:判断交叉和变异后的解是否更优,若非更优,则舍弃。
Step 8:更新狮王最优位置xk+1。
Step 9:判断是否达到最大迭代次数,未完成迭代次数转Step 3。
Step 10:输出最后一次迭代的狮王最佳位置,即所求问题的解,算法终止。
2.4 算法复杂度时间复杂度取决于实验中迭代次数、设置的种群数量和所求问题的规模,因此需要根据具体问题进行分析。
依据各模块时间复杂度计算总体时间复杂度可得,O(6N2+2N+5+lb103),算法时间复杂度呈多项式级别,去掉运行时间中的常数项、去掉各项系数,只保留最高项,去掉数量级小一级的N(因为N2的数据规模远大于N)最终化简为O(N2)。
3 实验结果及分析为验证所提算法的性能,搭建二维栅格地图进行实验,实验环境:操作系统Windows 11(64bit),处理器AMD Ryzen 7 5800H with Radeon Graphics. 3.20 GHz,运行内存16 G,仿真平台Matlab 2021a。
3.1 性能验证与分析本文选取9个标准函数进行测试,具体参考的标准函数见表 1。
| 函数序号 | 名称 | 维数 | 范围 | 最值 |
| f1 | Sphere | n | [-100, 100] | 0 |
| f2 | Schwefel 2.21 | n | [-10, 10] | 0 |
| f3 | Schwefel 2.22 | n | [-10, 10] | 0 |
| f4 | Ackly | n | [-32, 32] | 0 |
| f5 | Rastrigin | n | [-5, 5] | 0 |
| f6 | Griewank | n | [-600, 600] | 0 |
| f7 | Foxholes | 2 | [-65, 65] | 0.998 |
| f8 | Branin | 2 | [-5, 5] | 0.398 |
| f9 | Six-Hump | 2 | [-5, 5] | -1.031 |
为进一步说明改进的狮群算法(ILSO)的有效性,将与基础狮群算法(LSO)、灰狼算法(GWO)、遗传算法(GA)和粒子群算法(PSO)进行函数测试结果对比。为了保障对照实验的公平性,本次实验算法的参数设置一致,迭代次数50次,函数维度30维,种群规模为40。GA算法中pc=0.8,pm=0.1;PSO算法中c1=2,c2=2,w=0.8;灰狼算法中A=2,各种算法各独立运行10次,记录结果的平均值ave、标准差std和最优值。实验结果见表 2。
| 函数 | 指标 | ILSO | LSO | GWO | GA | PSO |
| ave | 2.15×10-22 | 1.97×10-10 | 4.12 | 5.75×103 | 2.96×103 | |
| f1 | std | 5.71×10-22 | 5.43×10-10 | 2.32×10 | 1.93×103 | 3.57×103 |
| fbest | 1.83×10-34 | 7.84×10-18 | 1.87×10 | 2.59×103 | 2.64×102 | |
| ave | 2.00×10-12 | 3.78×10-7 | 7.58 | 6.25×10 | 2.32×10 | |
| f2 | std | 5.02×10-12 | 5.77×10-7 | 1.50 | 7.98 | 1.50 |
| fbest | 0.00 | 0.00 | 4.05 | 5.30×103 | 1.59×10 | |
| ave | 5.11×10-11 | 7.21×10-7 | 1.61 | 2.46×10 | 2.86×10 | |
| f3 | std | 1.28×10-10 | 1.07×10-6 | 2.94×10-1 | 3.71 | 1.33×10 |
| fbest | 3.24×10-18 | 1.45×10-8 | 1.11 | 1.92×10 | 1.45×10 | |
| ave | 2.63×10-12 | 3.51×10-7 | 3.33 | 1.38×10 | 9.92 | |
| f4 | std | 5.90×10-12 | 6.38×10-7 | 3.64×10-1 | 1.40 | 3.23 |
| fbest | 8.88×10-16 | 4.35×10-14 | 2.63 | 1.15×10 | 6.19 | |
| ave | 0.00 | 3.99×10-12 | 5.11×10 | 1.28×102 | 1.66×102 | |
| f5 | std | 0.00 | 1.22×10-11 | 1.01×10 | 1.89×10 | 6.18×10 |
| fbest | 0.00 | 0.00 | 3.93×10 | 1.02×102 | 8.74×10 | |
| ave | 0.00 | 9.95×10-11 | 1.18 | 5.67×10 | 2.38×10 | |
| f6 | std | 0.00 | 2.70×10-10 | 1.57×10-1 | 1.47 | 1.45×10 |
| fbest | 0.00 | 0.00 | 1.05 | 3.92×10 | 4.68 | |
| ave | 1.24 | 1.68 | 5.02 | 2.56 | 1.91 | |
| f7 | std | 4.19×10-1 | 1.13 | 3.69 | 3.09 | 1.07 |
| fbest | 0.998 | 0.998 | 1.00 | 0.998 | 0.998 | |
| ave | 4.01×10-1 | 4.17×10-1 | 3.98×10-1 | 4.32×10-1 | 3.98×10 | |
| f8 | std | 3.37×10-3 | 5.44×10-2 | 5.61×10-4 | 3.32×10-2 | 2.01×10-2 |
| fbest | 0.398 | 0.398 | 0.398 | 0.401 | 0.398 | |
| ave | -1.01 | -1.02 | -1.031 | -1.01 | -1.031 | |
| f9 | std | 3.97×10-2 | 1.52×10-2 | 2.15×10-5 | 1.19×10-2 | 1.67×10-4 |
| fbest | -1.031 | -1.031 | -1.031 | -1.031 | -1.031 |
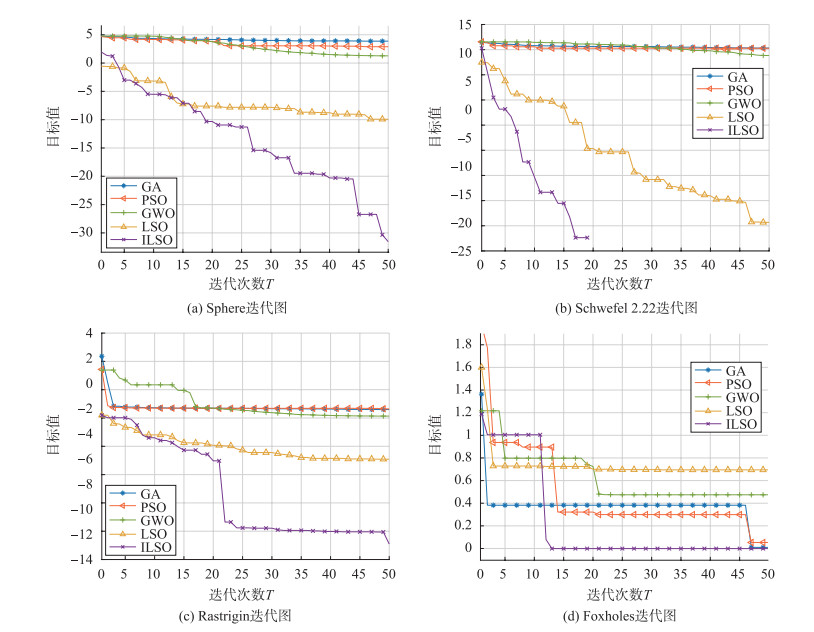
对于多维单峰测试函数f1、f2和f3,研究中所提出的ILSO算法在函数测试结果中,寻优结果最小,较对比算法提升了10~20个量级,这表明ILSO比其他4种算法具有更强的搜索能力和更高的搜索精度。同时加入调节因子和方向约束性函数的ILSO,在计算求解函数时,在5种算法中求得的平均值和标准差最小,说明ILSO算法具有较强的搜索能力和鲁棒性。
对于多峰测试函数f4、f5和f6而言,研究中所提的ILSO和LSO在f5和f6均能求得最优值,虽然在f4函数上并没有求的最优值,但f4的计算结果非常接近理论最优值0,且ILSO的均值和标准差更小,整体上ILSO收敛精度和稳定性优于LSO、GWO、GA和PSO,说明双种群平行结构有效的增加了算法寻优的能力,引入约束函数加强算法求解最优值的能力。
对于固维函数f7、f8和f9,由于维数降低,5种算法求解的准确率显著提高,表明在运算简单函数优化方面,5种算法的性能相差不大。
在选取的9个不同维度的测试函数中,本文所提及的ILSO算法,相比LSO算法寻优结果提升了10~20个量级,相比其他4种算法,ILSO算法稳定性更高。为了更直观反映算法性能的提升,图 5给出了部分函数的收敛曲线。
|
| 图 5 部分函数收敛图 Fig.5 Convergence graph of partial functions |
基于不同大小和不同复杂程度的栅格地图进行实验,验证本文提出的改进狮群算法(ILSO)在路径规划方面可行性。同时与传统的智能优化算法遗传算法(GA)和粒子群算法(PSO),新型智能优化算法狮群算法(LSO)和灰狼算法(GWO)进行对比。参数设置同3.1节。
3.2.1 20×20地图实验在相同的实验环境下,使用障碍物障碍物占比约为25%的小型20×20简单地图进行路径规划测试,为减少偶然性对实验的影响,进行10轮独立实验,取平均值,实验结果如图 6和表 3所示。
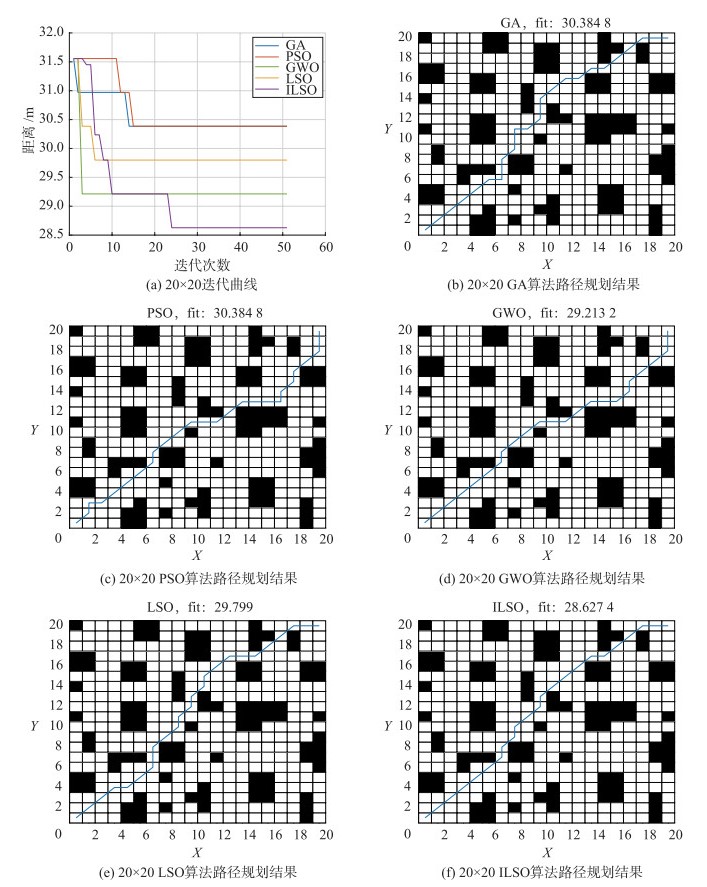
|
| 图 6 20×20地图实验结果 Fig.6 20×20 map experiment results |
| 算法 | 最优路径/m | 平均路径/m | 平均迭代次数/次 | 平均运行时间/s |
| GA | 30.384 8 | 30.627 4 | 3 | 1.220 7 |
| PSO | 30.384 8 | 30.802 0 | 33 | 1.001 8 |
| GWO | 29.213 2 | 29.501 8 | 25 | 0.903 7 |
| LSO | 29.799 0 | 29.956 0 | 40 | 0.987 9 |
| ILSO | 28.627 4 | 28.709 4 | 24 | 1.020 6 |
表 3结果显示,本文提出的ILSO算法在简单地图中,求解最优路径方面的能力,优于对比的4种算法。本文提出的ILSO求解得到的最路径为28.627 4 m,平均迭代次数为24次,时间为2.670 1 s,对比另外4种算法,路径平均缩短约4.41%,运行时间仅次于GWO算法,相比于LSO算法,ILSO算法运行时间减少了3.31%。
3.2.2 40×40地图实验在相同的实验环境下,使用障碍物占比约为33%的中型40×40复杂地图进行测试,实验结果如图 7和表 4。
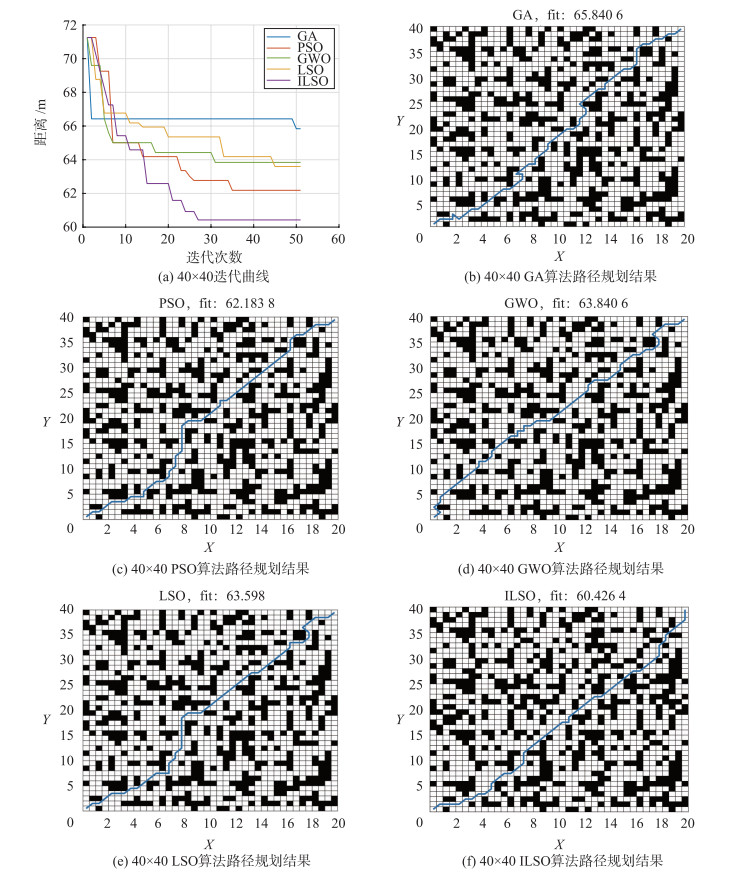
|
| 图 7 40×40地图实验结果 Fig.7 40×40 map experiment results |
| 算法 | 最优路径/m | 平均路径/m | 平均迭代次数/次 | 平均运行时间/s |
| GA | 65.840 6 | 66.623 2 | 42 | 3.351 6 |
| PSO | 62.183 8 | 64.355 3 | 35 | 2.644 9 |
| GWO | 63.840 6 | 65.012 2 | 31 | 2.594 0 |
| LSO | 63.598 0 | 65.941 1 | 45 | 2.718 4 |
| ILSO | 60.426 4 | 63.920 4 | 28 | 2.491 5 |
从图 7(a)可以看出,随着实验地图复杂程度的增加,5种算法的迭代次数和运行时间有不同程度的增加,可能是因为算法在解决复杂地图时,求解能力下降。
本文提出的ILSO求解得到的最优解为60.426 4 m,平均迭代次数为28次,时间为2.491 5 s,对比另外4种算法,路径平均缩短约5.35%,ILSO算法运行时间相比LSO算法缩短8.15%,随着地图更大、更复杂,ILSO算法的性能优势也变得更明显。
3.2.3 50×50地图实验在相同的实验环境下使用障碍物占比约为33%的50×50大型复杂地图进行测试,实验结果如图 8和表 5所示。
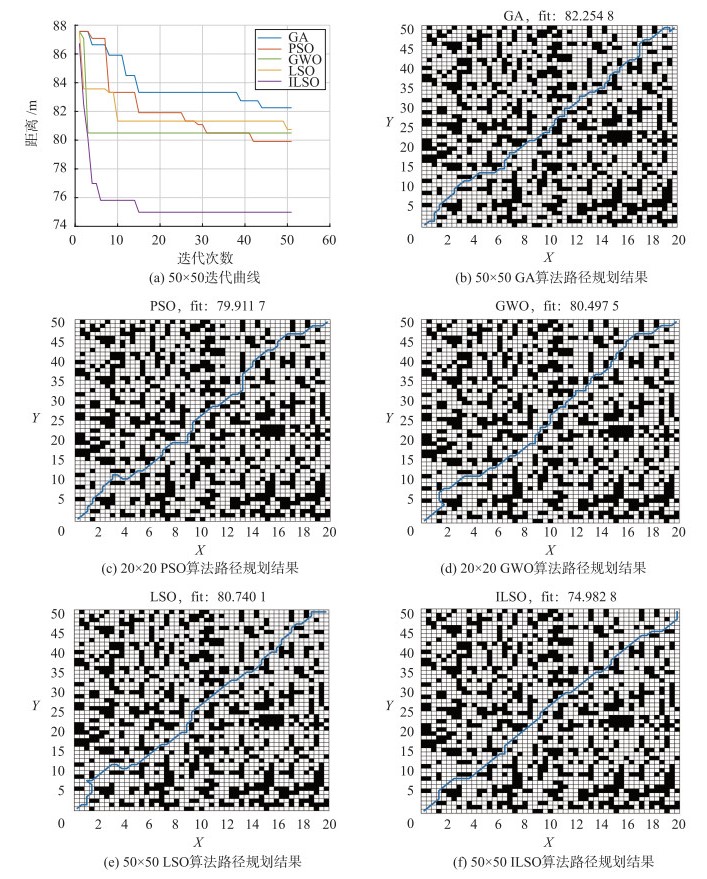
|
| 图 8 50×50地图实验结果 Fig.8 50×50 map experiment results |
| 算法 | 最优路径/m | 平均路径/m | 平均迭代次数/次 | 平均运行时间/s |
| GA | 82.254 8 | 83.924 6 | 44 | 7.850 1 |
| PSO | 79.911 7 | 81.292 4 | 42 | 3.354 9 |
| GWO | 80.497 5 | 80.902 6 | 3 | 3.953 4 |
| LSO | 80.740 1 | 82.128 6 | 48 | 4.297 6 |
| ILSO | 74.982 8 | 75.686 7 | 15 | 3.653 6 |
从图 8(a)可以看出,随着地图复杂度和地图幅度的提高,ILSO算法在求解路径规划问题的最短路径时优于其他算法,说明双种群结构的狮群算法有更强的搜索能力。
实验结果如表 5所示,本文所提出的ILSO求解最短路径方面,相比另外4种算法分别减少8.84%、6.17%、6.85%和7.13%,平均减少7.25%。5种算法种PSO算法运行时间最短,ILSO算法次之,相比LSO算法,运行时间减少了14.99%。实验数据表明,在更大更复杂的栅格地图中,双种群结构的ILSO算法寻优能力更强、运行时间更短。
3.2.4 路径平滑处理图 9为四阶贝塞尔曲线平滑处理的仿真图,随机生成一张50×50的ILSO路径规划路线进行路径平滑处理。平滑后的路径没有转角,移动曲线更加光滑,更适合机器人的移动,避免机器人在行走过程中急停和旋转。
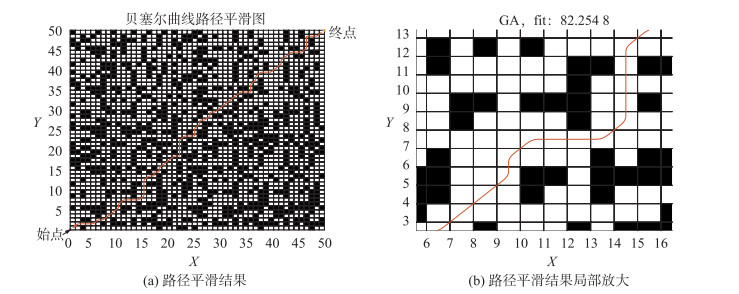
|
| 图 9 路径平滑处理 Fig.9 Convergence graph of partial functions |
设置的种群数量和迭代次数可能会影响实验结果,在其他参数不变的情况下,需要在40×40和50×50复杂地图进行参数敏感性实验。
为避免实验的偶然性,重复10次操作,取平均值。种群规模对路径长度的影响,如图 10所示。较小的种群规模得不到最优解,但种群规模不断增大,计算也会不断增大,且当种群规模超过一定数量,最优解并不会更小,因此,平衡各种因素,需要选取一个合适数量的种群规模。
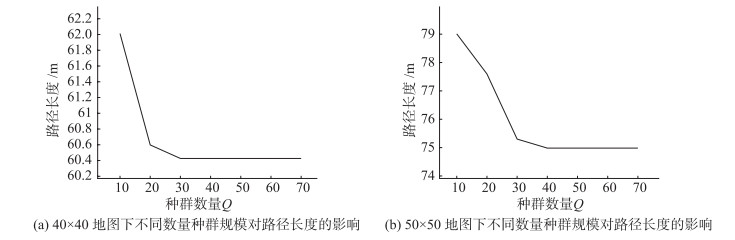
|
| 图 10 种群规模对路径长度的影响 Fig.10 Effect of population size on path length |
由图 10(a)可以看出,当种群数量Q=30左右时,求得的长度最短,由图 10(b),当种群数量Q=40左右时算法搜索到最短路径,考虑到算法的寻优能力,因此均取Q=40。
路径长短随迭代次数变化如图 11所示。
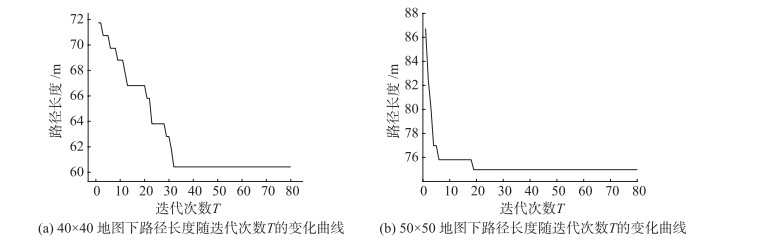
|
| 图 11 路径长度随迭代次数的变化曲线 Fig.11 Curves of path length versus iteration times |
由图 11可知,在不同地图大小的情况下ILSO算法在第30代和第20代之后开始逐渐收敛得到最优解,综合考虑计算时间等各种因素,迭代次数取T=50。
4 结论针对基础狮群算法搜索效率低、多样性不足等问题,提出了在狮群算法中使用了混沌种群初始化,提高算法初始解的质量和寻优效率,同时引入调节因子,提高算法多样性,避免算法早熟。接着针对路径规划问题,首先,针对狮群算法未指定狮群移动方向导致算法迭代次数增加,引入方向约束性函数,增加了算法的精度;其次,提出了一种双种群结构的狮群算法用以解决路径规划中出现的搜索效率低、运算时间长的问题;最后针对规划出的路径转角多的问题,运用四阶贝塞尔曲线对路径转角进行平滑处理。为验证算法改进的性能,首先使用算法求解9个国际标准测试函数,结果表明,改进后的ILSO算法求解能力更优;其次在栅格地图中运用算法求解最优路径,实验结果表明,改进后的ILSO算法在3张不同复杂程度和大小地图求解路径方面都优于改进前的算法和其他4种算法,并且在更大更复杂的栅格地图中,ILSO算法性能的提升更加显著,说明改进算法能更好适应复杂环境的路径规划,且平滑后的路径也更适合机器人移动。综上,研究中所提出的改进狮群算法能有效运用于路径规划当中。
但研究中还存在些许不足,如四阶Bezier曲线路径平滑处理计算量大、且只能在算法规划出路径后进行平滑处理,不能进行实时路径平滑,此外在路径规划中,没有考虑动态障碍物移动的情况下机器人的路径规划,改进后的算法性能仍有进步的空间,这些问题将在未来进一步探索和研究。
| [1] |
RUBIO F, VALERO F, LLOPIS-ALBERT C. A review of mobile robots: Concepts, methods, theoretical framework, and applications[J/OL]. International Journal of Advanced Robotic Systems. 2019[2022-01-16]. http://www.researchgate.net/publication/332469850. DOI: 10.1177/1729881419839596.
|
| [2] |
HART P E, NILSSON N J, RAPHAEL B. A formal basis for the heuristic determination of minimum cost paths[J]. IEEE Transactions on Systems Science and Cybernetics, 1968, 4(2): 100-107. DOI:10.1109/TSSC.1968.300136 |
| [3] |
王洪斌, 尹鹏衡, 郑维, 等. 基于改进的A*算法与动态窗口法的移动机器人路径规划[J]. 机器人, 2020, 42(3): 346-353. WANG H B, YIN P H, ZHENG W, et al. Mobile robot path planning based on improved A* algorithm and dynamic window method[J]. Robot, 2020, 42(3): 346-353. |
| [4] |
陈靖辉, 崔岩, 刘兴林, 等. 基于改进A*算法的移动机器人路径规划方法[J]. 计算机应用研究, 2020, 37(S1): 118-119. CHEN J H, CUI Y, LIU X L, et al. Mobile robot path planning method based on improved A* algorithm[J]. Computer Application Research, 2020, 37(S1): 118-119. |
| [5] |
KHATIB O. Real-time obstacle avoidance for manipulators and mobile robots[M]//Autonomous Robot Vehicles. Berlin, Germany: Springer, 1986: 396-404.
|
| [6] |
欧阳鑫玉, 杨曙光. 基于势场栅格法的移动机器人避障路径规划[J]. 控制工程, 2014, 21(1): 134-137. OUYANG X Y, YANG S G. Mobile robot obstacle avoidance path planning based on potential field grid method[J]. Control Engineering, 2014, 21(1): 134-137. DOI:10.3969/j.issn.1671-7848.2014.01.031 |
| [7] |
赵明, 郑泽宇, 么庆丰, 等. 基于改进人工势场法的移动机器人路径规划方法[J]. 计算机应用研究, 2020, 37(S2): 66-68, 72. ZHAO M, ZHENG Z Y, MO Q F, et al. Mobile robot path planning method based on improved artificial potential field method[J]. Computer Application Research, 2020, 37(S2): 66-68, 72. |
| [8] |
刘洋, 马建伟, 臧绍飞, 等. 基于融合Bezier优化遗传算法的路径规划[J]. 控制工程, 2021, 28(2): 284-292. LIU Y, MA J W, ZANG S F, et al. Path planning based on Bezier optimized genetic algorithm[J]. Control Engineering, 2021, 28(2): 284-292. |
| [9] |
魏彤, 龙琛. 基于改进遗传算法的移动机器人路径规划[J]. 北京航空航天大学学报, 2020, 46(4): 703-711. WEI T, LONG C. Mobile robot path planning based on improved genetic algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(4): 703-711. |
| [10] |
胡章芳, 程亮, 张杰, 等. 多约束条件下基于改进遗传算法的移动机器人路径规划[J]. 重庆邮电大学学报(自然科学版), 2021, 33(6): 999-1006. HU Z F, CHENG L, ZHANG J, et al. Path planning of mobile robot based on improved genetic algorithm under multiple constraints[J]. Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition), 2021, 33(6): 999-1006. |
| [11] |
陈嘉林, 魏国亮, 田昕. 改进粒子群算法的移动机器人平滑路径规划[J]. 小型微型计算机系统, 2019, 40(12): 2550-2555. CHEN J L, WEI G L, TIAN X. Smooth path planning of mobile robot based on improved particle swarm optimization algorithm[J]. Small Microcomputer System, 2019, 40(12): 2550-2555. DOI:10.3969/j.issn.1000-1220.2019.12.014 |
| [12] |
MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61. |
| [13] |
王永琦, 江潇潇. 基于混合灰狼算法的机器人路径规划[J]. 计算机工程与科学, 2020, 42(7): 1294-1301. WANG Y Q, JIANG X X. Robot path planning based on hybrid grey wolf algorithm[J]. Computer Engineering and Science, 2020, 42(7): 1294-1301. |
| [14] |
游达章, 康亚伟, 刘攀, 等. 一种改进灰狼优化算法的移动机器人路径规划方法[J]. 机床与液压, 2021, 49(11): 1-6. YOU D Z, KANG Y W, LIU P, et al. An improved grey wolf optimization algorithm for mobile robot path planning method[J]. Machine Tool and Hydraulic, 2021, 49(11): 1-6. |
| [15] |
刘生建, 杨艳, 周永权. 一种群体智能算法——狮群算法[J]. 模式识别与人工智能, 2018, 31(5): 431-441. LIU S J, YANG Y, ZHOU Y Q. A swarm intelligence algorithm-Lion swarm algorithm[J]. Pattern Recognition and Artificial Intelligence, 2018, 31(5): 431-441. |
| [16] |
汪婵婵. 基于改进狮群算法的汽轮机热耗率模型预测[J]. 计量学报, 2021, 42(7): 853-860. WANG C C. Prediction of steam turbine heat consumption rate model based on improved lion swarm algorithm[J]. Metrology Report, 2021, 42(7): 853-860. |
| [17] |
王艳红, 张革文. 基于改进狮群算法的云计算资源调度策略[J]. 计算机应用与软件, 2021, 38(11): 269-275. WANG Y H, ZHANG G W. Cloud computing resource scheduling strategy based on improved lion swarm algorithm[J]. Computer Application and Software, 2021, 38(11): 269-275. |
| [18] |
黄澄, 袁东风, 张海霞. 基于狮群算法的数字孪生车间调度问题优化[J]. 山东大学学报(工学版), 2021, 51(4): 17-23, 34. HUANG C, YUAN D F, ZHANG H X. Optimization of digital twin shop scheduling problem based on lion group algorithm[J]. Journal of Shandong University (Engineering Edition), 2021, 51(4): 17-23, 34. |
| [19] |
ZHAO F, LIU M, WANG K, et al. A soft measurement approach of wastewater treatment process by lion swarm optimizer-based extreme learning machine[J/OL]. Measurement, 2021[2021-11-30]. http://www.zhangqiaokeyan.com/journal-foreign-detail/0704028818717. DOI: 10.1016/measurement.2021.109322.
|
| [20] |
LIU J, LI D, WU Y, et al. Lion swarm optimization algorithm for comparative study with application to optimal dispatch of cascade hydropower stations[J/OL]. Applied Soft Computing, 2020[2021-04-05]. http://www.sciencedirect.com/science/article/pii/s1568494679307550. DOI: 10.1016/2020.105974.
|
| [21] |
QIAO W, LU H, ZHOU G, et al. A hybrid algorithm for carbon dioxide emissions forecasting based on improved lion swarm optimizer[J/OL]. Journal of Cleaner Production, 2020[2021-06-05]. https://kd.nsfc.gov.cn/achievementsystem/isisn/detail/Page/25717f963427f55630165e5346de6bbc0. DOI: 10.1016/2020.118612.
|
| [22] |
DURAKLI Z, NABIYEV V. A new approach based on Bezier curves to solve path planning problems for mobile robots[J/OL]. Journal of Computational Science, 2022[2022-07-01]. https://www.nstl.gov.cn/paper.detail.html?id=36e68 c214f721 cb6ac0e85f43ab1feab. DOI: 10.1016/2022.101540.
|
| [23] |
张金炜, 王文扬, 郭蓬, 等. 基于蚁群四次贝塞尔曲线的无人车路径规划[J]. 现代电子技术, 2019, 42(13): 113-116. ZHANG J W, WANG W Y, GUO P, et al. Unmanned vehicle path planning based on ant colony quartic Bezier curve[J]. Modern Electronic Technology, 2019, 42(13): 113-116. |
| [24] |
杨海东, 鄂加强. 自适应变尺度混沌免疫优化算法及其应用[J]. 控制理论与应用, 2009, 26(10): 1069-1074. YANG H D, E J Q. Adaptive variable scale chaotic immune optimization algorithm and its application[J]. Control Theory and Application, 2009, 26(10): 1069-1074. |
| [25] |
赵燕伟, 吴斌, 蒋丽, 等. 车辆路径问题的双种群遗传算法求解方法[J]. 计算机集成制造系统, 2004(3): 303-306. ZHAO Y W, WU B, JIANG L, et al. Solving method of bi-population genetic algorithm for vehicle routing problem[J]. Computer Integrated Manufacturing System, 2004(3): 303-306. |



