2. 西华师范大学电子信息工程学院, 四川 南充 637002;
3. 电子科技大学信息与通信工程学院, 四川 成都 611731;
4. 云南师范大学泛亚商学院, 云南 昆明 650092
2. School of Electronic Information Engineering, China West Normal University, Nanchong 637002, China;
3. School of Information and Communication Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China;
4. Pan-Asia Business School, Yunnan Normal University, Kunming 650092, China
0 引言
随着智慧城市和“中国制造2025”的不断深化,物联网(Internet-of-things,IoT)已遍布各行各业,成为后5G移动网络中重要的研究场景[1]。根据权威机构的统计结果,全球联网的IoT设备在2017年已达30. 35亿台,并且预计到2025年将突破75. 44亿台[2]。为便于大规模灵活部署,如何提高IoT设备的待机时间成为一个关键设计难题。区别于通过人工更换电池或者利用自然能源(如太阳能、风能等) 的方式,无线能量传输(wireless power transfer,WPT) 在IoT设备中嵌入能量捕获模块,使其可以将来自专用能量站或周围环境的射频信号转化为能量并存储起来,用于后续发送记录的监测数据,因此,基于WPT技术的IoT数据采集系统是一种更加实用、稳定、可控的解决方案,已受到了学术界和工业界的广泛关注[3-12]。
由于无人机(unmanned aerial vehicle,UAV)特有的空间移动性、部署灵活性以及空地间良好的信道环境,已有研究常采用无人机作为数据采集节点。文[3]在给定UAV一维航迹的情形下通过时隙划分最大化系统吞吐量。在相同的系统模型下,文[4]进一步考虑了最小化传输时间以及最小化功率开销问题。为充分挖掘UAV的移动性,文[5]在给定发射功率的情形下通过UAV航迹设计实现系统吞吐量、功率开销和能量捕获三者之间的性能折中。为进一步提升优化性能,文[6]联合时隙划分、功率控制和UAV航迹设计最小化功率开销。此外,文[7]和文[8]分别提出了基于优化理论和基于机器学习的用户调度机制。为提升瞬时性能,文[9]和[10]分别在单UAV和集群UAV场景下联合时隙划分、功率控制和UAV悬停位置设计最大化系统吞吐量。区别于时分多址接入(time division multiple access,TDMA)[3-10]等正交多址接入技术,非正交多址接入(non-orthogonal multiple access,NOMA)技术容许相同小区中多个用户使用相同维度的无线资源,能显著提高频谱效率和接入链路数目(系统容量)[11-12]。文[11]在基于UAV和NOMA的无线携能传输系统中联合功率分割因子和预编码最大化系统吞吐量并保证用户的安全通信。文[12]在基于UAV无线供能和NOMA的移动边缘计算系统中联合UAV悬停位置、波束赋形和计算资源分配最大化计算和速率。
综上所述,大部分已有研究均限制UAV基站在每个悬停位置仅服务单个IoT设备[3-8]。部分研究打破了上述限制并采用TDMA协议同时服务多个IoT设备,但需要对每个传输时隙进行异常精细的划分,这对IoT设备侧的同步精度提出了苛刻要求[9-10]。基于此,部分研究进一步引入NOMA协议,这虽能避免对传输时隙的划分但会产生较高的同频干扰并影响传输性能[11-12]。此外,在两种传输协议下,已有研究主要关注系统吞吐量[9-12]而忽略了用户公平性[13]。针对已有文献的上述不足,本文的创新点有:
1) 本文首先在TDMA协议和NOMA协议下分别联合时隙划分和功率控制最大化所有IoT设备中的最小传输速率(用户公平性指标)。特别地,在TDMA协议下,可通过数学分析和辅助变量将原问题等价转化为凸优化问题,继而在多项式时间内得到全局最优解(2. 1节中定理1)。在NOMA协议下则可借助分块坐标下降(block coordinate descent,BCD)算法,通过交替求解两个凸优化子问题收敛到原非凸问题的一个静止点(2.2节中定理2~定理4以及算法1)。
2) 为平衡传输性能与实现复杂度,本文进一步提出了两种基于定长时间切片的部分NOMA(fixed- length sliced partial NOMA,FSP-NOMA)协议并联合设计时间片分配和功率控制。第一种协议(记为FSP-NOMA1)限制了每个IoT设备所能接入的时间片数目以及每个时间片所能接纳的IoT设备数目,针对原混合整数优化问题,提出一种基于匹配理论的次优机制(2.3节中算法2)。第二种协议(记为FSP-NOMA2)去除了上述限制,针对原非凸问题,提出一种基于连续凸近似(successive convex approximation,SCA)算法的次优机制(2.4节中定理5、定理6及算法3、算法4)。
3) 在每种传输协议下,本文分别分析了所提资源分配机制的时间复杂度并讨论了实际部署方式(2.5节)。最后,仿真结果验证了传输性能与实现复杂度之间的折衷关系,并展示了所提机制的收敛性以及优化效果受传播环境、IoT设备数目和时间片数目等系统参数的影响。
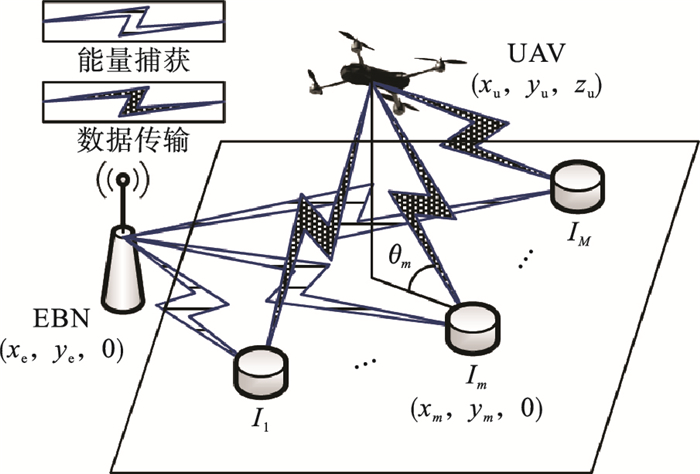
1 系统模型 1.1 系统设置如图 1所示,本文考虑一个基于WPT的IoT数据采集系统,包含1个位于地面的能量广播站(energy broadcasting node,EBN)、M个位于地面的IoT设备(本身不携带电池,完全借助能量捕获模块从EBN获取能量)和1个数据采集节点。不失一般性,本文考虑旋转翼UAV充当数据采集节点的情形,并假设在数据采集过程中所有网络节点的空间位置均保持不变[3-12],本文所提资源分配机制可与已有文献中的UAV航迹设计[3-7]或悬停位置设计[9-12]相结合。为便于后续描述,记IoT设备集合为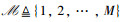
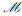
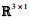
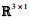
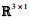
|
| 图 1 基于WPT的IoT数据采集系统 Fig.1 WPT-based IoT data collection system |
为简化后续分析,假设所有网络节点的发射端和接收端都只有一根全向天线。记从EBN发射端到Im接收端的信道增益为gm=ρmdm-τ/2∈ 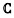
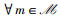
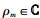
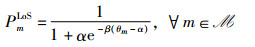
|
(1) |
其中,α和β都是与传播环境和载波频率相关的系统常数,θm表示从Im发射端到UAV接收端的仰角,即θm=180°/π×arcsin(zu/Lm),其中,Lm=‖wu-wmI‖表示UAV与Im之间的欧氏距离。相应地,上述G2A链路为NLoS链路的概率为PmNLoS=1-PmLoS。对于任意一种分量,总的路径损耗由两部分构成:1) 自由空间路径损耗;2) 由于地面建筑物引起的阴影效应和散射所导致的路径损耗,已有研究中仅考虑其均值[14]。特别地,当G2A链路为LoS链路或NLoS链路时,路径损耗可分别表示为[14]
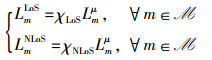
|
(2) |
其中,μ表示自由空间传播环境下的路径损耗因子,χLoS和χNLoS分别表示在两种情况下额外路径损耗的均值且满足χNLoS>χLoS。综上所述,G2A链路的路径增益可表示为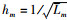
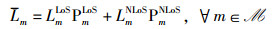
|
(3) |
不失一般性,本文假设G2A链路的信道增益hm满足|h1|2≥ |h2|2≥…≥ |hM|2。
1.3 问题构建每个时隙长度为T(小于信道的相干时间)且包括两个阶段:1) 能量传输/能量捕获阶段:每个IoT设备接收从EBN发送的无线信号并将其转化为能量,在此阶段,Im从EBN捕获到的能量可表示为
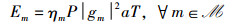
|
(4) |
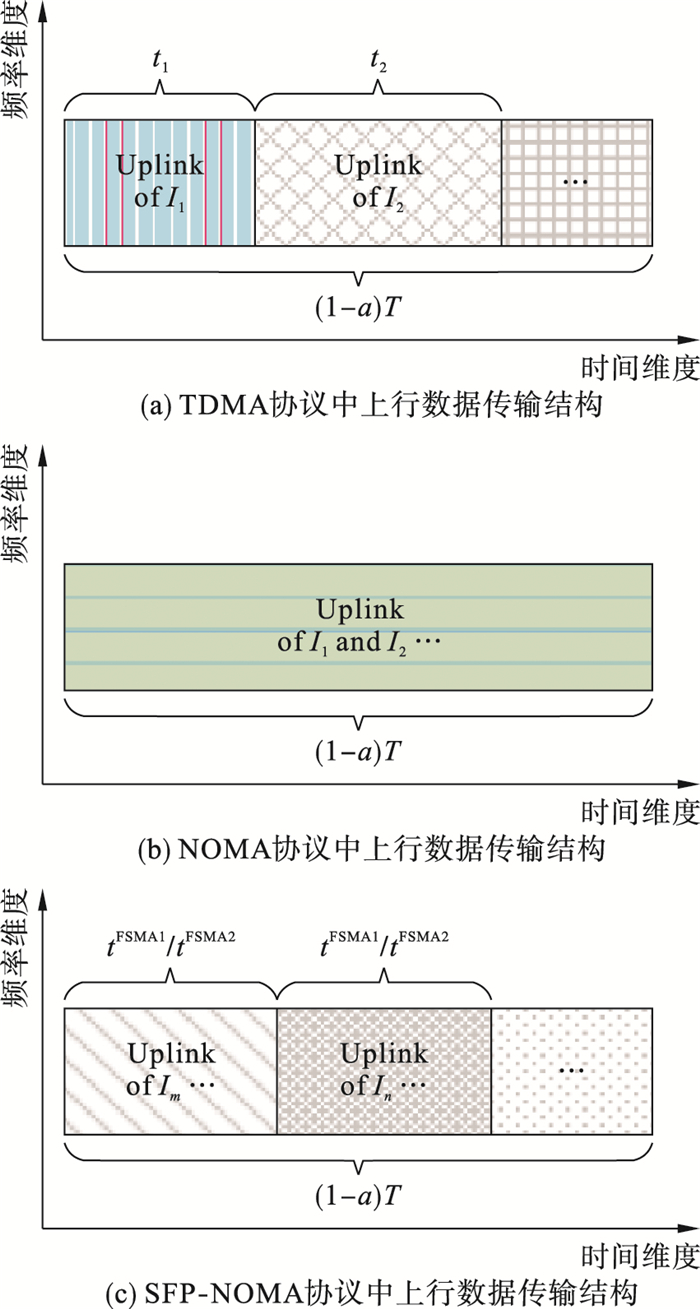
其中,0≤ηm≤1表示Im侧的能量转换效率,P表示EBN侧的固定发射功率,a表示第1个阶段在整个时隙T中的占比。2) 数据采集/数据传输阶段:每个IoT设备利用捕获到的能量发送数据到UAV,在整个时隙T中的占比为1-a。在此阶段,本文考虑4种传输协议,分别是TDMA、NOMA以及两种FSP-NOMA协议,一种FSP-NOMA协议限制每个IoT设备最多接入一个时间片且每个时间片最多接纳K个IoT设备,记为FSP-NOMA1,而另一种FSP-NOMA协议则去除了上述限制,记为FSP-NOMA2。4种传输协议的上行信道结构如图 2所示,接下来将分别描述4种传输协议下对应的资源分配问题。
|
| 图 2 各通信协议下的上行数据传输结构 Fig.2 Uplink data transmission structure under each communication protocol |
如图 2(a)所示,由于采用TDMA协议进行上行数据传输,故UAV在解码Im的复信号xm∈ 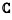
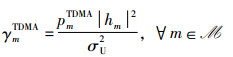
|
(5) |
其中,σU2表示零均值加性高斯白噪声的方差。基于香农公式,Im的上行归一化传输速率可定义为
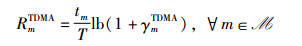
|
(6) |
为提升用户公平性,本文联合时隙划分和功率控制最大化所有IoT设备中的最低传输速率,相应的数学优化问题可构建为P1:
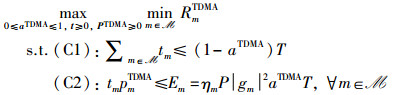
|
其中,向量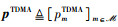
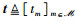
如图 2(b)所示,当采用NOMA协议进行上行数据传输时,所有IoT设备在整个第2个阶段复用相同信道,由于无需对传输时隙进行划分,故大幅度降低了对IoT设备侧同步精度的要求,但是用户间的同频干扰不可避免。基于上行NOMA的实现原理[11-13],UAV按照信道增益|hm|2的值从高到低依次解码IoT设备的信号,特别地,当UAV解码Im的信号xm时会受到来自Im+1,Im+2,…,IM的同频干扰,故相应的信干噪比(signal-to-interference-plus-noise ratio,SINR)可表示为

|
(7) |
其中,pmNOMA表示Im的发射功率。基于香农公式,Im的上行归一化传输速率可定义为
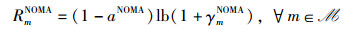
|
(8) |
其中,aNOMA表示在NOMA协议下能量捕获阶段在整个时隙中的占比。本文在NOMA协议下同样联合时隙划分和功率控制最大化所有IoT设备中的最低传输速率,相应的数学优化问题可构建为P2:
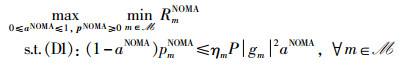
|
其中,向量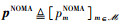
当数据传输阶段采用TDMA协议时,虽可借助成熟的凸优化算法得到全局最优解(见2.1节),但该协议对IoT设备侧的同步精度提出了苛刻要求。此外,当数据传输阶段采用NOMA协议时,虽可利用BCD算法收敛到原非凸问题的一个静止点(将在2.2节展示),但该协议会引入严重的同频干扰继而降低传输性能。为平衡传输性能和实现复杂度,本文进一步设计了FSP-NOMA1协议。如图 2(c)所示,为降低对IoT设备侧同步精度的要求,FSP-NOMA1协议将数据传输阶段划分为N个等长的时间片,即每个时间片时长为tFSMA1=(1-aFSMA1)T/N,其中,aFSMA1表示FSP-NOMA1协议下能量捕获阶段在整个时隙中的占比,记时间片集合为S
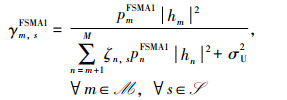
|
(9) |
其中,pmFSMA1表示Im的发射功率。基于香农公式,Im的上行归一化传输速率可定义为
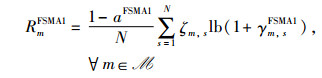
|
(10) |
在FSP-NOMA1协议下,本文联合时隙划分、时间片分配和功率控制最大化所有IoT设备中的最低传输速率,相应的数学优化问题可构建为P3:
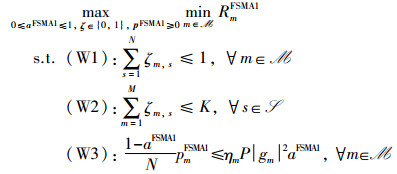
|
其中,矩阵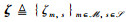
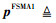
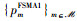
相比于TDMA协议和NOMA协议,虽然FSP-NOMA1协议可实现传输性能和实现复杂度的折中,但限制了每个IoT设备所能接入的时间片数量以及每个时间片所能接纳的IoT设备数量,这在一定程度上制约了传输性能。因此,本文进一步设计了FSP-NOMA2协议,与FSP-NOMA1协议类似,数据传输阶段被划分为Q个等长的时间片,即每个时间片时长为tFSMA2=(1-aFSMA2)T/Q,其中,aFSMA2表示在FSP-NOMA2协议下能量捕获阶段在整个时隙中的占比,记时间片集合为J
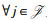
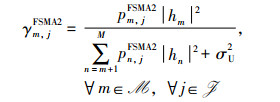
|
(11) |
基于香农公式,Im的上行归一化传输速率可表示为
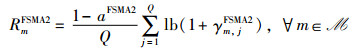
|
(12) |
在FSP-NOMA2协议下,本文同样联合时隙划分、时间片分配和功率控制最大化所有IoT设备中的最低传输速率,相应的数学优化问题可构建为P4:
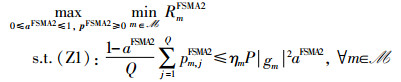
|
其中,矩阵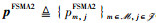
不难验证,P1中目标函数并不是关于优化变量的凹函数,且约束条件(C2)是经典的双线性不等式,其可行域并不是凸集[16],但是借助数学分析和辅助变量,可将P1等价转化为凸优化问题,详细过程见下述定理1。
定理1 P1可等价转化为凸优化问题。
证明 由式(5)和式(6)可知,P1中目标函数关于pTDMA是单调非降的。结合约束条件(C2),P1取得最优时必满足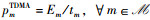
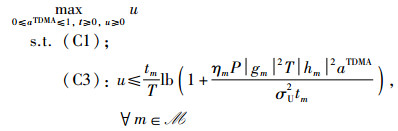
|
通过简单的算术运算,约束条件(C3)可简化为(C4):
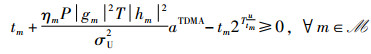
|
注意到,不等式左侧第3项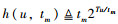
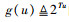
对于带有约束的凸优化问题P5,可借助成熟的凸优化算法保证在多项式时间内得到全局最优解,如内点法和拉格朗日对偶法等[16],与此同时,也可借助商用的数学优化工具箱,如CVX和MOSEK等。记最优解为aTDMA*和tm*,则最优的发射功率为pmTDMA*=ηmP|gm|2aTDMA*T/tm*。
2.2 NOMA协议下资源分配机制的设计区别于P1,P2无法等价转化为凸优化问题,但当功率控制变量pmNOMA或时隙划分变量aNOMA给定时,剩余的子问题均属于凸优化问题。基于上述特性,本文利用BCD算法[17-18]得到次优的时隙划分和功率控制策略。在BCD算法的第r次迭代中,时隙划分子问题和功率控制子问题的特性分别由定理2和定理3给出。
定理2 当功率控制变量给定时,剩余的时隙划分子问题属于凸优化问题且最优解为aNOMA(r)* = 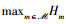
证明 对于任意给定的发射功率向量pNOMA(r),定义:
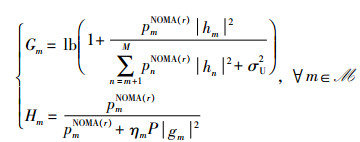
|
(13) |
其中,Gm≥0和0≤Hm≤1均是常数,则P2可简化为P6:
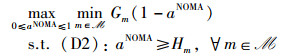
|
注意到,Gm(1-aNOMA),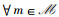
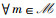
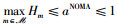
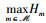
定理3 当时隙划分变量给定时,剩余的功率控制子问题属于凸优化问题。
证明 对于任意给定的时隙划分aNOMA(r),功率控制子问题可表示为P7:
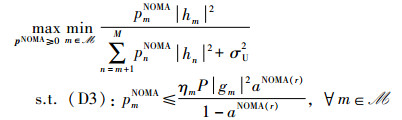
|
首先,引入非负辅助变量v表示所有IoT设备中的最低SINR并将P7重写为P8:

|
经过简单的算术运算,P8可等价转化为P9:
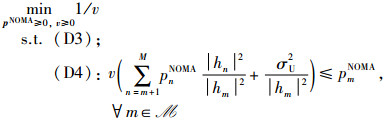
|
其次,引入新变量w=ln v和qm=ln pmNOMA,∀m∈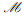
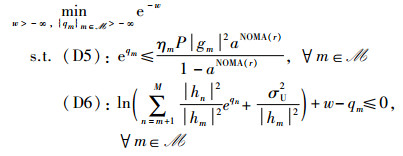
|
约束条件(D5)中不等式左侧为凸函数,故其可行域为凸集。约束条件(D6)中不等式左侧第1项是经典的log-sum-exp函数,属于凸函数[16],而后两项均是线性函数,故约束条件(D6)的可行域表示凸函数的0下水平集(0-sublevel set),故同样为凸集[16],综上,P10是在若干个凸集的交集上最小化一个凸函数,故P10属于凸优化问题[16]。证毕。
类似于P5,对于带有约束的凸优化问题P10,可借助成熟的凸优化算法或商用的数学优化工具箱在多项式时间内得到全局最优解,继而再通过pmNOMA=eqm,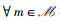
基于定理2和定理3,利用BCD算法求解P2的详细过程如算法1所示。为了便于后续描述,记P2的目标函数为O(aNOMA,pNOMA)。
算法1 NOMA协议下基于BCD算法的资源分配机制
输入 初始化设置r=1为当前迭代次数,V1为最大迭代次数,δ为误差门限,(pNOMA(1),aNOMA(1))为初始点。
步骤1 在给定pNOMA(r)下,利用定理2得到(P6)的最优解aNOMA(r)*。
步骤2 在给定aNOMA(r)*下,利用定理3和成熟的凸优化算法得到(P7)的最优解pNOMA(r)*。
步骤3 如果相邻迭代的性能之差小于误差门限,即O(aNOMA(r)*,pNOMA(r)*)-O(aNOMA(r),pNOMA(r)) < δ,则算法收敛;否则,如果r≥V1,则停止迭代;否则,更新pNOMA(r+1)=pNOMA(r)*、aNOMA(r+1)=aNOMA(r)*和r=r+1,并返回步骤1。
输出 输出次优的时隙划分和功率控制策略(aNOMA(r)*,pNOMA(r)*)。
此外,算法1的收敛性可由下述定理4给出。
定理4 序列{O(aNOMA(r)*,pNOMA(r)*)}r≥1是单调非降的且算法1一定在多项式时间内收敛。
证明 在算法1中,步骤1是在给定pNOMA(r)*下得到P6的最优解aNOMA(r+1)*,则存在不等式:
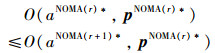
|
(14) |
类似地,步骤2是在给定aNOMA(r+1)*下得到P7的最优解pNOMA(r+1)*,则存在不等式:
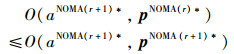
|
(15) |
结合式(14)和式(15)得到
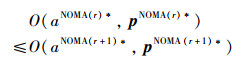
|
(16) |
式(16)表明,P2的目标函数值在迭代过程中是单调非降的。由于P2的目标函数是连续的且其最优值是有限的,故算法1一定会收敛[17]。此外,由于每次迭代中仅需求解两个凸优化问题,故上述收敛过程一定在多项式时间内完成。证毕。
需要说明的是,如果交换算法1中变量的优化顺序,不难证明其同样可收敛到原非凸问题的一个静止点,然而不同优化顺序下静止点的性能可能各不相同,而且还取决于初始点的位置。
2.3 FSP-NOMA1协议下资源分配机制的设计P3是一个混合整数优化问题,一般意义下属于非确定性多项式时间难问题[19-20]。为降低求解复杂度,本文将原问题分解为时隙划分子问题与联合时间片分配和功率控制子问题。针对时隙划分子问题,可直接采用2. 2节中所提机制。不失一般性,可使FSP-NOMA1协议和NOMA协议具有相同的数据传输时长,从而保证两种算法的可比性。针对联合时间片分配和功率控制子问题,本文提出一种基于匹配理论的近似优化机制,保证在多项式时间内得到高效次优解。为便于后续描述,记时间片s为ls。
定义1 IoT设备集合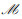
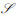
1) 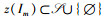
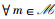
2) 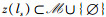
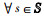
3) z(Im)={ls}当且仅当Im∈z(ls),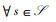
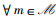
其中,1) 表示每个Im最多接入一个时间片,对应于约束条件(W1);2) 表示每个ls最多接纳K个IoT设备,对应于约束条件(W2);3) 表示Im和ls之间配对的相互性。
对于经典的配对问题,即任意集合中元素的配对性能仅取决于配对对象而与其它元素的配对结果无关,可借助推迟录用算法收敛到原问题的一个稳定点[21]。但对于本节中P3,任意IoT设备的传输性能不仅取决于其所在的时间片,而且取决于位于相同时间片的其它IoT设备,即配对过程具有外部效应(externalities)[22]。针对具有外部效应的配对问题,可引入交换稳定性的概念,并通过不断消除交换拥塞对收敛到一个稳定点,但上述过程需遍历所有的配对情形,继而会产生指数时间复杂度[22]。针对上述挑战,本文提出了一种基于好感度的动态配对算法。不同于推迟录用算法,在好感度中考虑了不同IoT设备之间的相互影响,而且会随着配对过程而动态变化。其次,所提机制保证在每次迭代中至少实现一组配对,故至多在M次迭代内实现收敛(多项式时间复杂度)。此外,所提机制可以保证分配到相同时间片的IoT数目不超过上限值K。
1) 好感度列表的构建:为与P3中目标函数保持一致,Im对于时间片ls的好感度定义为,当其分配到时间片ls后,ls上所有IoT设备获得的最优用户公平性Rm,sopt,其中,Rm,sopt是问题P11的最优目标函数值:
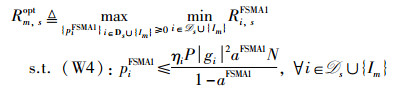
|
其中,集合
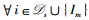
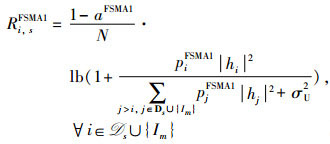
|
(17) |
由于P11与P7具有相同的问题结构,故可以利用定理3以及成熟的凸优化算法得到P11的最优解。
定义2 Im对ls1的好感度高于ls2当且仅当Rm,s1opt>Rm,s2opt,上述关系可表示为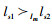
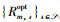
2) 动态配对算法的设计:为便于后续描述,引入集合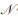
算法2 FSP-NOMA1协议下基于匹配理论的资源分配机制
输入 初始化设置
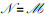
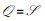
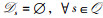
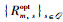
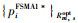
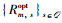
步骤1 集合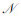
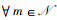
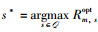
步骤2 当接收到多个接入请求时,每个时间片仅保留好感度最高的IoT设备而拒绝剩余的。对于时间片s,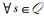
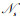
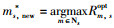
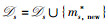
步骤3 根据IoT设备的接入情况更新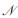
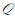
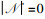
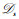
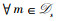
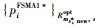
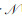
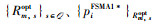
输出 输出次优的时间片分配和功率控制策略(ζ*,pFSMA1*)。
相比于P3,P4虽消除了二元时间片分配变量,但由于多IoT设备之间复杂的同频干扰,其属于非凸问题[15]。针对上述挑战,本文设计了基于BCD算法和SCA算法[23-24]的迭代优化机制,得到次优的时隙划分、时间片分配和功率控制策略。特别地,在BCD算法的第r次迭代中,当发射功率变量(已蕴含了时间片分配)固定为pFSMA2(r)时,剩余的时隙划分子问题可表示为P12:
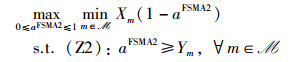
|
其中,Xm和Ym定义由式(18)给出。
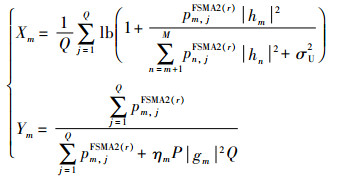
|
(18) |
注意到,P12与P6具有相同的问题结构,故可利用定理2得到其最优解,即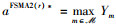
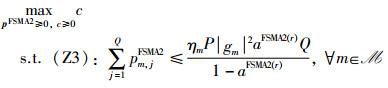
|
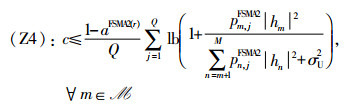
|
不难看出,约束条件(Z4)中不等式右侧包含了多个分式的函数和,无法借助变量变换等价转化为凹函数[25],故P13仍然为非凸问题。本节后续将对上述约束进行近似处理,继而借助SCA算法收敛到一个高效次优解。
通过简单的算术运算,P13中的约束条件(Z4)可改写为
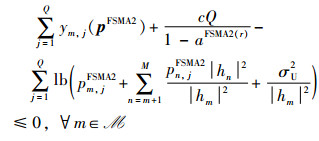
|
(19) |
其中,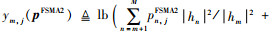
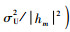
针对函数ym,j(pFSMA2)的非凸特性,在可行域中任意给定的功率控制矩阵pFSMA2(k)处对ym,j(pFSMA2) 进行1阶泰勒级数展开,从而恢复凸函数特性,展开结果为
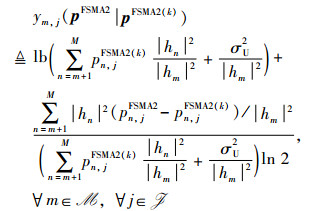
|
(20) |
其中,ym,j(pFSMA2|pFSMA2(k)) 为ym,j(pFSMA2)的全局上界函数。经过上述处理,P13中的约束条件(Z4)被近似为Z5:
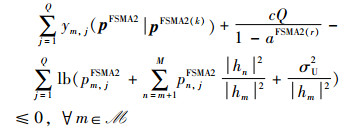
|
而原非凸问题P13则近似为P14:
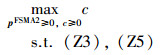
|
不难验证,约束条件(Z3)为线性不等式,而(Z5)则表示凸函数的0-下水平集,因此,P14是在若干个凸集的交集上最大化一个凹函数,故属于凸优化问题[16]。类似于P5和P10,可借助成熟的凸优化算法保证在多项式时间内得到P14的全局最优解[16]。
需要注意的是,上述最优解仅仅是在给定点pFSMA2(k)处的局部最优,若要进一步提升优化效果,则需通过迭代过程不断更新给定点位置:在第k次迭代,记P14的最优解为(pFSMA2(k)*,c(k)*),则可用其更新第k+1次迭代中给定点的位置,即pFSMA2(k+1)=pFSMA2(k)*。为便于后续描述,记P13的目标函数为U(pFSMA2,c),则利用SCA算法求解P13的详细过程如算法3所示。
算法3 求解P13的SCA算法
输入 初始化设置k=1为当前迭代次数,V2为最大迭代次数,δ为误差门限,(pFSMA2(1),c(1))为初始给定点。
步骤1 借助成熟的凸优化算法求解凸优化问题(P14),得到其最优解(pFSMA2(k)*,c(k)*)。
步骤2 若相邻迭代的性能之差小于误差门限,即U(pFSMA2(k)*,c(k)*)-U(pFSMA2(k),c(k)) < δ,则算法收敛;若k≥V2,则终止迭代;否则,更新pFSMA2(k+1)=pFSMA2(k)*、c(k+1)=c(k)*和k=k+1,返回步骤1。
输出 输出次优的功率控制策略pFSMA2(r)*。
算法3的收敛性见定理5。
定理5 序列{U(pFSMA2(k)*,c(k)*)}k≥1是单调非降的且能在多项式时间内收敛到P13的一个KKT(Karush-Kuhn-Tucker)点[16]。
证明 记式(19)的不等号左侧为fm(pFSMA2,c),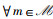
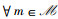
1) 对于P14可行域内的任意点(pFSMA2,c),U(pFSMA2,c)≥U(k)(pFSMA2,c);
2) U(pFSMA2(k)*,c(k)*)=U(k+1)(pFSMA2(k)*,c(k)*) 和fm(pFSMA2(k)*,c(k)*)=fm(k+1)(pFSMA2(k)*,c(k)*),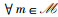
3) ▽U(pFSMA2(k)*,c(k)*)=▽U(k+1)(pFSMA2(k)*,c(k)*) 和▽fm(pFSMA2(k)*,c(k)*)=▽fm(k+1)(pFSMA2(k)*,c(k)*),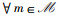
首先,根据P14最优解的定义可知,U(k+1)(pFSMA2(k+1)*,c(k+1)*)≥U(k+1)(pFSMA2(k)*,c(k)*)。由条件1)和条件2)可知,U(pFSMA2(k+1)*,c(k+1)*)≥U(k+1)(pFSMA2(k+1)*,c(k+1)*)和U(k+1)(pFSMA2(k)*,c(k)*)=U(pFSMA2(k)*,c(k)*)。综合以上3个关系式可得,U(pFSMA2(k+1)*,c(k+1)*)≥U(pFSMA2(k)*,c(k)*),即序列{U(pFSMA2(k)*,c(k)*)}k≥1是单调非降的。此外,由于U(pFSMA2,c)的连续性,序列{U(pFSMA2(k)*,c(k)*)}k≥1必然在有限次迭代次数内收敛到P13的局部最大值。此外,由于可在多项式时间内得到P14的最优解,故算法3会在多项式时间内收敛。当(pFSMA2(k)*,c(k)*)=(pFSMA2(k+1)*,c(k+1)*)时,即算法3收敛且(pFSMA2(k)*,c(k)*)满足第k+1次迭代中P14的KKT条件,由条件2)和条件3)可知,(pFSMA2(k)*,c(k)*)也满足P13的KKT条件。证毕。
最后,当数据传输采用FSP-NOMA2协议时,求解P4的详细过程如算法4所示。为便于后续描述,记P4的目标函数为F(aFSMA2,pFSMA2)。
算法4 FSP-NOMA2协议下基于BCD算法的资源分配机制
输入初始化设置r=1为当前迭代次数,V3为最大迭代次数,(pFSMA2(1),aFSMA2(1))为初始点,δ为误差门限。
步骤1 在给定pFSMA2(r)下利用定理2求解P12,得到其最优解aFSMA2(r)*。
步骤2 在给定aFSMA2(r)*下利用算法3求解P13收敛到其KKT点pFSMA2(r)*。
步骤3 若相邻迭代的性能之差小于误差门限,即F(aFSMA2(r)*,pFSMA2(r)*)-F(aFSMA2(r),pFSMA2(r)) < δ,则算法收敛;若r≥V3,则终止迭代;否则,更新pFSMA2(r+1)=pFSMA2(r)*,aFSMA2(r+1)=aFSMA2(r)*和r=r+1,并返回步骤1。
输出 输出次优的时隙划分和功率控制策略(aFSMA2(r)*,pFSMA2(r)*)。
此外,算法4的收敛性可由定理6给出。
定理6 序列{F(aFSMA2(r)*,pFSMA2(r)*)}r≥1是单调非降的且算法4一定在多项式时间内收敛。
证明 首先,存在不等式:
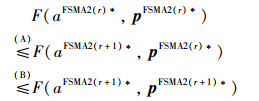
|
(21) |
由算法4的步骤1可知,在给定pFSMA2(r)*下,aFSMA2(r+1)*是P12的最优解,故(A)成立;由定理5可知,在给定aFSMA2(r+1)*下,对于算法3的每次迭代,P13的目标函数值是单调非降的,故(B)成立。因此,在算法4的每次迭代后,P4的目标函数值是单调非降的。不难验证,P4的目标函数是连续的且其最优值是有限的,故算法4一定会收敛[17]。此外,在算法4的每次迭代中,只需借助定理2求解P12并借助算法3求解有限多个凸优化问题P14,故算法4必在多项式时间内完成。证毕。
2.5 时间复杂度和实际部署方式本节首先在每种传输协议下分别分析所提资源分配机制的时间复杂度:
1) 在TDMA协议下,原联合时隙划分和功率控制问题P1等价于带有约束的凸优化问题P5,故可借助内点法求取最优解且时间复杂度可表示为O((M+2)4)[16],其中M+2为P5中优化变量的数目。
2) 在NOMA协议下,本文提出了基于BCD算法的资源分配机制(算法1),在每次迭代中交替求解两个凸优化子问题,特别地,可通过数学分析得到时隙划分子问题最优解的闭式表达式,并借助内点法求解功率控制子问题,故整个机制的时间复杂度可表示为O(V1(1+(M+1)4)),其中V1为BCD算法的最大迭代次数,M+1为功率控制子问题中优化变量的数目。
3) 在FSP-NOMA1协议下,本文提出了基于匹配理论的联合时间片分配和功率控制机制(算法2)。由于信道增益的随机性,事先无法分析出配对的推进过程,继而无法得到准确的时间复杂度。作为参考,此处分析最差时间复杂度,最差情形出现在当每次迭代中所有未接入的IoT设备都向同一个时间片发送配对请求且最终都接入该时间片,故迭代次数等于IoT设备的数目且时间复杂度可表示为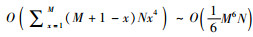
4) 在FSP-NOMA2协议下,本文提出了基于BCD算法和SCA算法的双层迭代机制:对于基于SCA算法的内层迭代机制(算法3),其时间复杂度可表示为O(V2(MQ+1)4),其中V2为SCA算法的最大迭代次数,MQ+1为凸优化子问题中优化变量的数目;基于此,对于基于BCD算法的外层迭代机制(算法4),其时间复杂度可表示为O(V3(1+V2(MQ+1)4)),其中V3为BCD算法的最大迭代次数。
本节进一步讨论所提资源分配机制的实际部署方式,关键在于分析它们是否可在线计算资源分配策略,这取决于IoT设备所采集数据的时延(实时性)需求Treq、无线信道的相干时间Tcoh(在相干时间内可认为信道增益不变)以及算法在实现过程中的时间开销Talg。当IoT业务类型和无线环境确定后,Treq和Tcoh将为定值,所以关键在于分析Talg,其主要由两个部分组成:1) 获取参数信息的时间;2) 运行算法以及分发资源分配策略的时间。在本文中,资源分配问题所需的参数信息包括:IoT设备侧的能量捕获速率ηmP|gm|2;IoT设备与UAV基站之间的上行信道增益|hm|2;UAV基站接收端的背景噪声功率σU2、时隙长度T以及与时间片复用相关的参数(K,N,Q)。在能量捕获和数据传输之前,IoT设备可独立测量ηmP|gm|2并结合UAV基站侧的参考信号测量|hm|2,之后将它们通过上行控制链路反馈给UAV基站。当UAV基站收集到全部参数信息后便可利用所提资源分配机制计算资源分配策略并分发给所有IoT设备。如果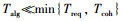
在仿真中,所有IoT设备均匀分布在一个边长为20 m的方形区域内,EBN距离上述区域中心50 m,UAV位于上述区域中心正上空且飞行高度为110 m。对于EBN与IoT设备之间的地面链路,路径损耗因子为τ=3. 5,信道衰落服从均值为0且方差为1的复高斯分布。对于IoT设备与UAV之间的地空链路,自由空间传播环境下的路径损耗因子为μ=2,其它信道参数如表 1所示[14]。特别地,本文考虑3种信道传播环境,分别是郊区、标准城市和密集城市。此外,设置UAV接收端的噪声方差为σU2=1×10-12. 5 mW,时隙长度为T=0. 2 s,EBN侧的固定发射功率为P=1×105 mV,假设所有IoT设备具有相同的能量转换效率,即ηm=0. 9,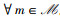
| 参数 | 郊区 | 标准城市 | 密集城市 |
| α | 4.886 | 9.617 7 | 12.087 |
| β | 0.429 | 0.158 1 | 0.113 9 |
| χLoS/dB | 0.1 | 1 | 1.6 |
| χNLoS/dB | 21 | 20 | 23 |
在算法1中,设置V1=10,初始发射功率pNOMA(1)为元素全是1. 25×10-5 mW的向量,aNOMA(1)=0. 1。在算法4中,设置V2=50,V3=10,初始发射功率pFSMA2(1)为元素全是1. 25×10-5 mW的矩阵,aFSMA2(1)= 0. 1。在算法1、算法3和算法4中,误差门限都设置为δ=10-6。在实现中,仿真平台采用Python,建模工具使用AMPLPY和CVXPY,优化工具使用IPOPT和MOSEK,具体来说,利用AMPLPY 0. 7.1 (https://ampl.com/products/api/#Python)描述P5和算法1每次迭代中的P10,借助IPOPT 3.14.4(https://github.com/coin-or/Ipopt)进行求解。此外,利用CVXPY 1.1.15(https://www.cvxpy.org/)描述算法3每次迭代中的P14,借助MOSEK 9.3.6(https://www.mosek.com/)进行求解。仿真结果都是100次独立测试结果的平均。
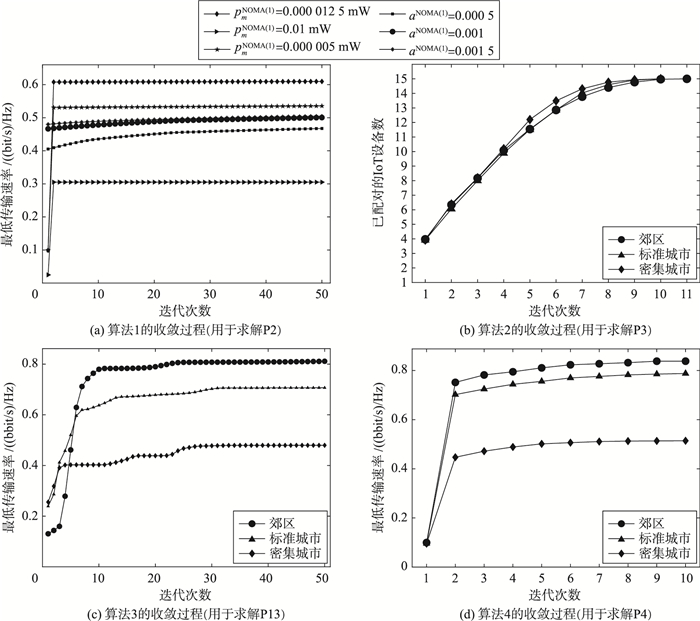
图 3展示了在后3种数据传输协议下所提资源分配机制的收敛性(固定IoT设备数目为M=15)。需要说明的是,在基于TDMA的数据传输协议下,资源分配的设计可等价转化为凸优化问题(定理1),故可直接借助成熟的凸优化算法或优化工具得到最优解,无需迭代设计。后续将进一步对比4种数据传输协议下资源分配机制的优化性能。可以看出:1) 如图 3(a)所示(郊区场景),NOMA协议下基于BCD算法的机制具有良好的收敛性,平均只需要2次迭代便可收敛。此外,算法的收敛性还会随着变量的优化顺序和初始点位置而变化,在6组对比结果中,先优化时隙划分变量且将初始发射功率变量均设置为1. 25×10-5 mW具有最佳的优化性能。2) 如图 3(b)所示,FSP-NOMA1协议下基于匹配理论的机制平均需要10次迭代便可收敛到一个稳定点,迭代次数少于IoT设备数目,时间复杂度远低于2. 5节中分析的最差情形。3) 如图 3(c)所示,FSP-NOMA2协议下基于SCA算法的内层机制平均需要约25次迭代可收敛到原非凸问题的一个KKT点,良好地实现了算法性能与运算复杂度之间的折中。与此同时,如图 3(d)所示,FSP-NOMA2协议下基于BCD算法的外层机制平均需要约8次迭代收敛到一个静止点。表 2给出了4种传输协议下所提资源分配机制的平均运算时间,相比于P1~P3,P4包含更多的优化变量继而具有更高的求解难度,为得到高效近似解,算法4需更多的迭代次数和更长的运算时间。根据测量结果[27],信道的相干时间一般在秒数量级(1 s~10 s),结合2.5节分析可知,TDMA和NOMA传输协议下的资源分配机制可在线部署,而两种FSP-NOMA传输协议下的资源分配算法则需要结合深度学习理论,通过离线方式训练基于深度神经网络的在线模型。4) 结合图 3(a)、图 3(c)和图 3(d),P2、P13和P4的目标函数值均随着迭代过程呈现单调非降特性且能在有限迭代次数内收敛,这与定理4、定理5和定理6中结论保持一致。5) 随着信道传播环境的恶化(从郊区到标准城市再到密集城市),地空信道中的非视距分量增加,平均路径损耗增大,但这并不会影响各迭代算法的收敛性。
|
| 图 3 在不同信道传播环境下所提算法1到算法4的收敛性能 Fig.3 The convergenceof the proposed algorithm 1 to algorithm 4 under different channel propagation environment |
| 传输协议 | 平均运算时间/s |
| TDMA | 0.126 5 |
| NOMA | 1.278 6 |
| FSP-NOMA1 | 17.831 4 |
| FSP-NOMA2 | 65.308 7 |
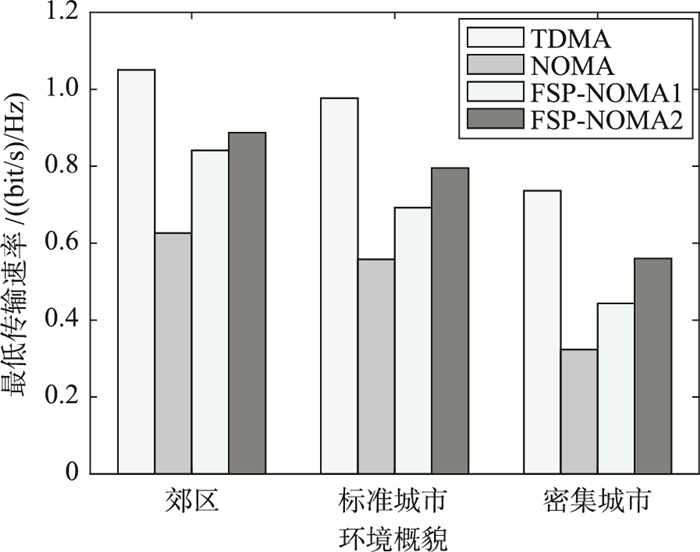
图 4对比了4种数据传输协议下所提机制的优化性能(固定IoT设备数目为M=15)。可以看出:1) TDMA协议通过精细的时隙划分保证所有IoT设备通过正交方式接入系统,由于彻底避免了用户之间的同频干扰,每个IoT设备为获得特定传输速率所需的功率开销最小,提高了时隙和功率利用率,继而获得最高的传输性能。2) 除TDMA外的3种协议中都不同程度地引入了同频干扰,降低了能量效率,故优化性能低于TDMA协议,特别地,NOMA协议虽容许多用户复用相同频谱,可用于支持后5G移动网络中海量IoT场景[1],但这是以降低能量效率为代价的。3) 相比于NOMA协议,两种FSP-NOMA协议在不同程度上分散了用户间的同频干扰,故得到更高的传输性能。此外,相比于FSP-NOMA1协议,FSP- NOMA2协议消除了频谱复用约束,能够充分利用系统中的多用户分集增益进行干扰协调,故带来了更高的优化性能,特别是在标准城市和密集城市场景,但结合图 3可知,上述增益是以更高的运算复杂度为代价的。4)从郊区到标准城市再到密集城市,由于地面建筑物高度和密度的增加,致使信道传播环境逐渐变差,故4种数据传输协议下的最低传输速率都依次降低。
|
| 图 4 4种数据传输协议下所提机制的性能对比 Fig.4 Performance comparisons among the proposed mechanisms under four data transmission protocols |
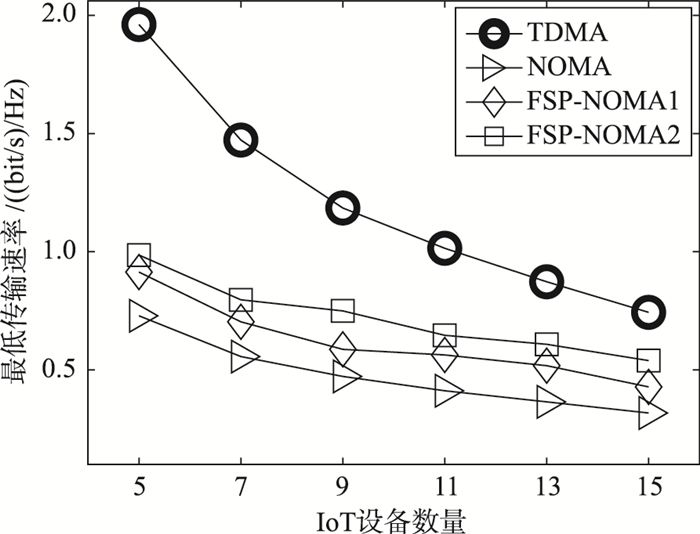
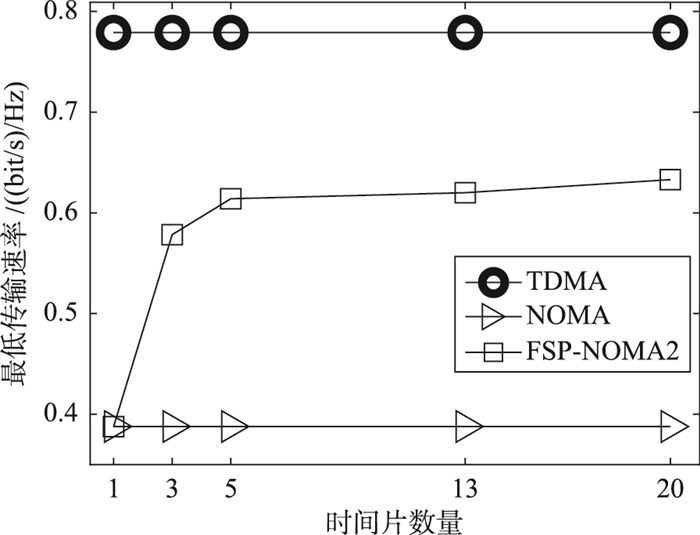
图 5展示了所提资源分配机制性能随IoT设备数目的变化趋势(密集城市场景)。可以看出:随着IoT设备数目的增加,TDMA协议可通过精细划分传输时隙实现多用户接入,但由于系统是频带受限的,故优化性能会呈现大幅度降低。相反,系统在其他3种协议都是干扰受限的,通过设计高效的资源分配机制可有效实现干扰协调,故受IoT设备数目增加的影响较小。结合优化性能,当IoT设备数目较多时,FSP-NOMA2协议不失为一种合理的选择。图 6进一步展示了FSP-NOMA2协议性能随着时间片数量Q的变化趋势(密集城市场景,固定IoT设备数目为M=15)。可以看出:当时间片数量为1时,FSP-NOMA2协议等价于NOMA协议。随着时间片数目的增加,FSP-NOMA2协议可以借助资源分配机制有效规避用户间的同频干扰,性能逐渐接近TDMA协议。特别地,当时间片数目趋近于无穷大时,FSP-NOMA2协议等价于TDMA协议。在后5G海量IoT场景中,FSP-NOMA2协议是一种有效的解决方案,可以根据IoT设备侧的同步精度,合理设置传输时隙中时间片数目,从而实现传输性能与实现复杂度之间的折衷。
|
| 图 5 所提机制性能受IoT设备数目的影响 Fig.5 The impact of the number of IoT devices on the performance of the proposed mechanisms |
|
| 图 6 FSP-NOMA2协议下机制性能受时间片数目的影响 Fig.6 The impact of the number of slices on the performance of the mechanism under FSP-NOMA2 protocol |
在基于WPT的IoT数据采集系统中,本文考虑了4种数据传输协议并分别设计了面向用户公平性的高效资源分配机制。仿真结果验证了所提机制的收敛性和有效性,虽然采用TDMA协议可以获得最高的传输性能,但是对IoT设备侧的同步精度提出了苛刻要求;此外,NOMA协议虽避免了对于传输时隙的划分,但会引入严重的同频干扰继而恶化传输性能。为实现传输性能与实现复杂度之间的折衷,本文进一步提出了两种FSP-NOMA协议,然而相应的资源分配模型属于混合整数问题和非凸问题,为进一步平衡算法性能与运算复杂度,分别设计了基于匹配理论和SCA算法的次优机制。在后续研究中,将探索如何利用机器学习理论[5, 8, 17, 19, 26]在保证优化性能的前提下降低时间复杂度,从而满足高可靠性低时延IoT场景中的通信需求。
| [1] |
范平志, 李里, 陈欢, 等. 面向大规模物联网的随机接入: 现状、挑战与机遇[J]. 通信学报, 2021, 42(4): 1-21. FAN P Z, LI L, CHENG H, et al. Random access for massive internet of things: Current status, challenges and opportunities[J]. Journal on Communications, 2021, 42(4): 1-21. |
| [2] |
杨毅宇, 周威, 赵尚儒, 等. 物联网安全研究综述: 威胁、检测与防御[J]. 通信学报, 2021, 42(8): 188-205. YANG Y Y, ZHOU W, ZHAO S R, et al. Survey of IoT security research: Threats, detection and defense[J]. Journal on Communications, 2021, 42(8): 188-205. |
| [3] |
YE H T, KANG X, JOUNG J, et al. Optimization for wireless-powered IoT networks enabled by an energy-limited UAV under practical energy consumption model[J]. IEEE Wireless Communications Letters, 2021, 10(3): 567-571. DOI:10.1109/LWC.2020.3038079 |
| [4] |
YE H T, KANG X, JOUNG J, et al. Optimization for full-duplex rotary-wing UAV-enabled wireless-powered IoT networks[J]. IEEE Transactions on Wireless Communications, 2020, 19(7): 5057-5072. DOI:10.1109/TWC.2020.2989302 |
| [5] |
YU Y, TANG J, HUANG J Y, et al. Multi-objective optimization for UAV-assisted wireless powered IoT networks based on extended DDPG algorithm[J]. IEEE Transactions on Communications, 2021, 69(9): 6361-6374. DOI:10.1109/TCOMM.2021.3089476 |
| [6] |
YANG Z D, XU W, SHIKH-BAHAEI M. Energy efficient UAV communication with energy harvesting[J]. IEEE Transactions on Vehicular Technology, 2020, 69(2): 1913-1927. DOI:10.1109/TVT.2019.2961993 |
| [7] |
XIE L F, XU J, ZHANG R. Throughput maximization for UAV-enabled wireless powered communication networks[J]. IEEE Internet of Things Journal, 2019, 6(2): 1690-1703. DOI:10.1109/JIOT.2018.2875446 |
| [8] |
LHAZMIR S, OUALHAJ O A, KOBBANE A, et al. UAV for wireless power transfer in IoT networks: A GMDP approach[C/OL]//IEEE International Conference on Communications. Piscataway, USA: IEEE, 2020[2021-12-15]. https://ieeexplore.ieee.org/document/9148956/. DOI: 10.1109/ICC40277.2020.9148956.
|
| [9] |
JIANG M, LI Y Q, ZHANG Q, et al. Joint position and time allocation optimization of UAV enabled time allocation optimization networks[J]. IEEE Transactions on Communications, 2019, 67(5): 3806-3816. DOI:10.1109/TCOMM.2019.2896973 |
| [10] |
YE H T, KANG X, JOUNG J, et al. Joint uplink-and-downlink optimization of 3-D UAV swarm deployment for wireless-powered IoT networks[J]. IEEE Internet of Things Journal, 2021, 8(17): 13397-13413. DOI:10.1109/JIOT.2021.3065689 |
| [11] |
WANG W, TANG J, ZHAO N, et al. Joint precoding optimization for secure SWIPT in UAV-aided NOMA networks[J]. IEEE Transactions on Communications, 2020, 68(8): 5028-5040. DOI:10.1109/TCOMM.2020.2990994 |
| [12] |
FENG W M, TANG J, ZHAO N, et al. Hybrid beamforming design and resource allocation for UAV-aided wireless-powered mobile edge computing networks with NOMA[J]. IEEE Journal on Selected Areas in Communications, 2021, 39(11): 3271-3286. DOI:10.1109/JSAC.2021.3091158 |
| [13] |
QU H, TANG R, ZHAO J H, et al. Performance tradeoff between user fairness and energy conservation in downlink NOMA systems[C/OL]//IEEE International Conference on Communications Workshops. Piscataway, USA: IEEE, 2018[2021-12-08]. https://ieeexplore.ieee.org/document/8403607/. DOI: 10.1109/ICCW.2018.8403607.
|
| [14] |
SOHAIL M F, LEOW C Y, WON S H. Energy-efficient non-orthogonal multiple access for UAV communication system[J]. IEEE Transactions on Vehicular Technology, 2019, 68(11): 10834-10845. DOI:10.1109/TVT.2019.2939186 |
| [15] |
TANG R, ZHAO J H, QU H, et al. User-centric joint admission control and resource allocation for 5G D2D extreme mobile broadband: A sequential convex programming approach[J]. IEEE Communications Letters, 2017, 21(7): 1641-1644. DOI:10.1109/LCOMM.2017.2681664 |
| [16] |
BOYD S, VANDENBERGHE L. Convex optimization[M]. Cambridge, UK: Cambridge University Press, 2004.
|
| [17] |
HONG M Y, RAZAVIYAYN M, LUO Z Q, et al. A unified algorithmic framework for block-structured optimization involving big data: With applications in machine learning and signal processing[J]. IEEE Signal Processing Magazine, 2016, 33(1): 57-77. DOI:10.1109/MSP.2015.2481563 |
| [18] |
YANG G, YUAN D D, LIANG Y C, et al. Optimal resource allocation in full-duplex ambient backscatter communication networks for wireless-powered IoT[J]. IEEE Internet of Things Journal, 2019, 6(2): 2612-2625. DOI:10.1109/JIOT.2018.2872515 |
| [19] |
TANG R, ZHANG R Z, XIA Y M, et al. Joint mode selection and power allocation for NOMA systems with D2D communication[C]//IEEE/CIC International Conference on Communications in China. Piscataway, USA: IEEE, 2021: 606-611.
|
| [20] |
黄玉蕾, 唐睿, 罗晓霞, 等. LTE-A蜂窝网络下设备直通中的联合信道分配和功率控制方案[J]. 信息与控制, 2017, 46(2): 231-237, 256. HUANG Y L, TANG R, LUO X X, et al. Joint channel assignment and power control for D2D communication underlaying LTE-A cellular networks[J]. Information and Control, 2017, 46(2): 231-237, 256. |
| [21] |
TANG R, QU H, ZHAO J H, et al. Distributed resource allocation for IBFD-enabled NOMA systems[J]. IEEE Communications Letters, 2018, 22(11): 2318-2321. DOI:10.1109/LCOMM.2018.2870425 |
| [22] |
PANTISANO F, BENNIS M, SAAD W, et al. Matching with externalities for context-aware user-cell association in small cell networks[C]//IEEE Global Communications Conference. Piscataway, USA: IEEE, 2013: 4483-4488.
|
| [23] |
MARKS B, WRIGHT G. A general inner approximation algorithm for nonconvex mathematical programs[J]. Operation Research, 1978, 26(4): 681-683. DOI:10.1287/opre.26.4.681 |
| [24] |
TANG R, CHENG J, CAO Z X. Joint placement design, admission control, and power allocation for NOMA-based UAV systems[J]. IEEE Wireless Communications Letters, 2020, 9(3): 385-388. DOI:10.1109/LWC.2019.2956702 |
| [25] |
SHEN K M, YU W. Fractional programming for communication systems-Part Ⅰ: Power control and beamforming[J]. IEEE Transactions on Signal Processing, 2018, 66(10): 2616-2630. DOI:10.1109/TSP.2018.2812733 |
| [26] |
TANG R, ZHANG R Z, ZHAO Y H, et al. Power allocation for NOMA-based two-way full-duplex relaying systems[C]//IEEE/CIC International Conference on Communications in China. Piscataway, USA: IEEE, 2021: 1077-1082.
|
| [27] |
HERBERT S, WASSELL I, LOH T H, et al. Characterizing the spectral properties and time variation of the in-vehicle wireless communication channel[J]. IEEE Transactions on Communications, 2014, 62(7): 2390-2399. DOI:10.1109/TCOMM.2014.2328635 |



