2. 北京科技大学工程技术研究院, 北京 100083
2. Engineering Technology Research Institute, Beijing University of Science and Technology, Beijing 100083, China
0 引言
随着现代工业规模发展,在目前工程应用中涌现出越来越多的多参数非线性优化问题,这些问题对提高产品质量、降低能耗至关重要。当采用传统智能优化算法如人工蜂群算法、遗传算法、粒子群优化算法等来解决该问题时,常常会出现计算复杂、收敛速度慢、适用性差等问题。其中,人工蜂群算法[1-3]作为新兴的群智能算法,是为优化代数问题提出的一种基于蜜蜂行为机制的元启发式算法,可通过模拟蜜蜂之间的角色转换与分工协作来解决多变量全局优化问题,是一种结构相对简单、鲁棒性强且基于种群的随机优化算法[4],因而相对其他算法具有较大的挖掘潜力,对解决该类问题具有一定优势。
为提高人工蜂群算法的寻优性能,很多学者开展了大量的研究工作,主要包括交叉改进与自身改进两方面的内容。其中,交叉改进是将人工蜂群算法与一些其他传统智能优化算法做创新组合,来提高算法性能;自身改进主要是有针对性地改进人工蜂群算法基本原理中的某一个或者某些环节,来提高算法本身的寻优能力。在交叉改进研究方面,2017年,刘刚等设计了一种混合离散人工蜂群算法,并与传统启发式算法和贪心随机自适应搜索算法路径重连,成功地缩短了流水车间调度完工总时间[5],但算法适用范围有限。2018年,叶奕茂等以粒子群优化(PSO)算法为基础,提出一种PSO-ABC智能混合算法,该混合算法在优化性能等方面得到明显提升[6],但在处理复杂多峰搜索算法时性能较差。2021年,蒋伟等为优化家庭能源管理系统模型,将差分进化算法的变异、交叉算子等加入到跟随蜂阶段中,改进后的算法更易跳出局部最优[7],但同时算法运算复杂度也大大增加。在自身改进研究方面,2018年,李宏娟等提出一种增强型ABC优化算法,通过调节新蜜源的分配策略等来估计异步电机转矩,该改进算法能快速估计出电机参数[8],但应用于不同异步电机中优化效果差距较大。2021年,管雪梅等通过调整人工蜂群算法中蜜蜂的搜索半径,在提高全局收敛性的前提下提升了算法精细搜索能力,使径向基函数神经网络参数得到一定程度的优化[9],但优化精度依然有待提升。综上所述,目前对于传统人工蜂群算法的改进方案虽已展开了大量深入的研究,但主要以交叉改进类算法研究较多,且部分改进后的算法实现困难,运行结果不稳定,算法精度依然有待提高。神经- 内分泌- 免疫系统是人体生理指标重要调控系统,通过神经引导、内分泌激素调控、免疫定向等生物机制来保障人体各项指标处于精准平衡稳态。这些生物引导、调控、定向生物机制,可以为进一步研究改进人工蜂群算法以解决多参数非线性优化问题提供新的研究途径。
基于人体神经- 内分泌- 免疫系统的生物调节机制,本文提出一种生物优化的人工蜂群智能算法(NEI-ABC智能算法)。该算法是在传统人工蜂群算法中增设蓝光引导单元、蜜源调控单元、触角定向单元,3个单元协同作用使该算法在寻优精度、收敛速度及跳出局部最优能力等方面均得到提升。与其他优化算法的对比仿真结果表明,NEI-ABC智能算法相对其他算法具有更优的寻优性能。
原油生产的注采规划等是一种典型的复杂多参数优化问题,注入流量与采出产量之间呈现出严重的非线性,目前已有产量递减方程、遗传算法[10-11]等应用于原油注采规划中,但仍存在实现复杂、精度低及优化速度慢等问题。为了进一步解决该类问题,将NEI-ABC算法应用于原油生产的注采优化问题中,实验结果表明该算法在速度与精度方面均表现最优。
1 相关理论基础 1.1 生物调节机制神经- 内分泌- 免疫系统是以共享化学信号分子为通用语言进行信息交流,构成整体性功能的系统。神经- 内分泌- 免疫系统内的生物调节机制为调节人体生命活动的主要机制,人体内的生物调节机制主要由神经引导机制、免疫定向机制、内分泌调控机制构成,三者之间存在双向的信息传递与复杂的调控作用,从而能够维持生物体内各类激素水平稳定在正常范围。
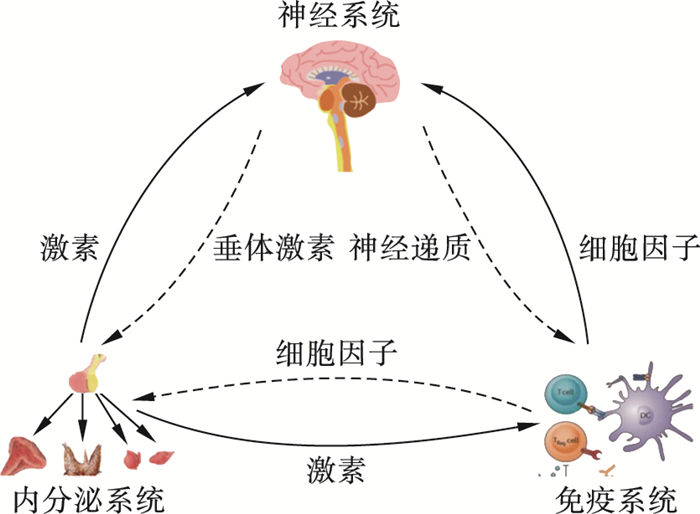
神经系统、免疫系统、内分泌系统三者之间的相互作用关系可表示成图 1所示的形式,神经系统产生的神经递质可通过突触联系调节钙离子通道,进而影响免疫系统发挥作用;同时神经细胞上也存在免疫调节的受体,影响神经系统的相关活动。除神经系统可影响免疫细胞外,内分泌激素也可以调控免疫反应的强弱,例如生长抑素属于免疫抑制类激素,而生长激素属于免疫增强类激素;相反,免疫系统也可以通过免疫细胞上的激素受体来对内分泌系统的调控机制产生影响。内分泌系统可以通过激素调节神经突触的传递效率,例如甲状腺激素能够提高神经系统的兴奋性;神经调节也可以直接影响到一些腺体的分泌活动,例如交感神经活动增强时肾上腺素分泌增多。本文以3大系统之间的相互作用为依据,综合神经引导机制、免疫定向机制、内分泌调控机制的作用原理与特点来对传统人工蜂群算法进行改进和优化。
|
| 图 1 NEI系统内的相互作用示意图 Fig.1 Interactions within the NEI system |
神经系统是机体内对生理功能活动的调节起主导作用的系统,分为中枢神经系统和周围神经系统两大部分,其基本单位为神经元,起引导作用的物质是神经递质,神经递质就存储在神经元轴突末端的突触小泡中。当生理指标发生变化时,主要由神经引导机制维稳调控。
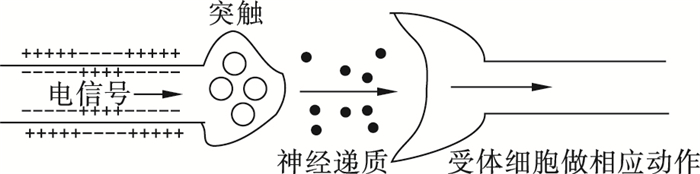
神经引导机制:当神经元受到刺激时,动作电位会沿着神经元移动并达到轴突终端,导致神经元的去极化。膜电位发生变化从而使电压门控离子通道打开,钙离子进入,为释放神经递质做准备。钙离子激活一种酶,使囊泡与突触蛋白分离,释放神经递质到突触间隙。突触间隙的神经递质与突触后膜结合,影响其所处状态,从而引导细胞做出相应动作。如图 2所示,神经系统通过释放神经递质作用于相关受体,从而引导细胞所处的状态发生改变,实现信息传递的作用,具有快速、灵敏的特点;其作用是由神经递质分泌原理来确定的,如式(1)所示[12]:
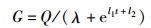
|
(1) |
|
| 图 2 神经引导机制示意图 Fig.2 Diagram of nerve guidance mechanism |
式中,G为神经递质的浓度变化量;Q为外部刺激量,反映调节作用的强弱;λ为固定常数;l1、l2为系统参数;t为时间,在t=0之前细胞内或组织液中的神经递质浓度相对稳定,当t=0时刻受到刺激后呈现式(1)所表示的变化规律。
1.1.2 免疫定向机制免疫系统可看作一个由细胞、组织和器官形成的巨大网络结构,是人体实现免疫应答、保护人体健康的系统[13-14]。白细胞是免疫系统中的一个重要成员,分布在血液和淋巴系统内,持续不断地搜索并识别外来抗原。
免疫定向机制:血液中的白细胞发现并识别抗原后,可精准地吞噬这种抗原与被感染的细胞,不损害健康细胞;同时白细胞还拥有记忆功能,当免疫细胞识别出抗原后便会记下抗原信息,并利用这些信息来识别外来入侵者,当再次遇到相同抗原时能快速调出相应抗体保护机体免受伤害。
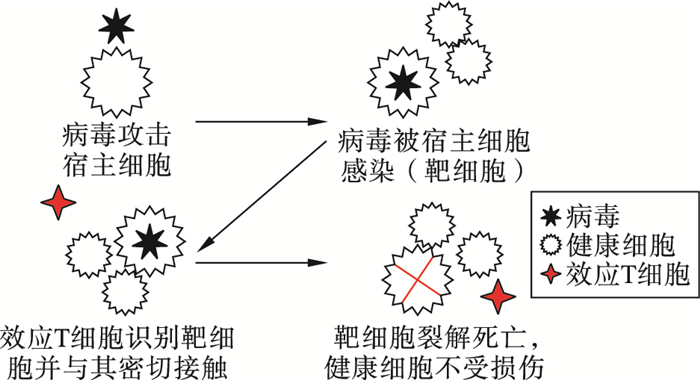
免疫细胞通过抗原决定簇来识别抗原,具有定向、精确的特点,此特点应用于智能优化算法中可使算法局部性能得到提升。其相关作用机制如图 3所示。
|
| 图 3 免疫定向机制示意图 Fig.3 Diagram of immune targeting mechanism |
内分泌系统由内分泌腺构成,包括垂体、甲状腺、胰腺等,当内分泌腺受到某些刺激时就会向体液中释放某种特异性物质——激素,以此来调节细胞激素分泌,从而协调人体内各个器官的工作。例如,甲状腺是人体内分泌系统的重要组成部分,能分泌促进生长发育与提高神经系统兴奋性的甲状腺激素。
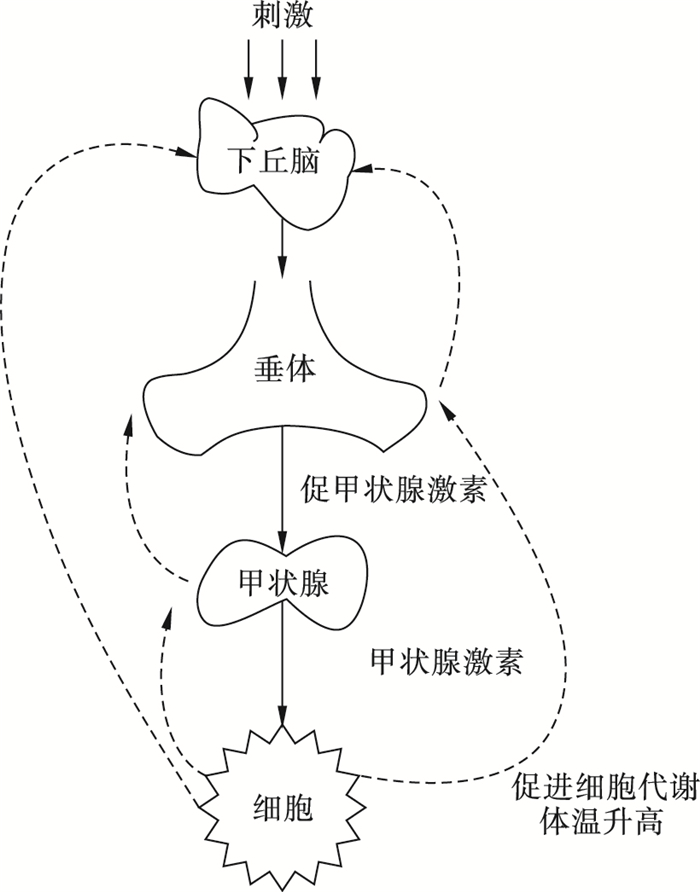
内分泌调控机制:当寒冷、紧张等刺激信号被下丘脑接收时,人体的内分泌调控机制会采用下丘脑-垂体-甲状腺的分级调节方式,调节新陈代谢,达到维持体温的目的。内分泌系统分泌的激素通过体液等运输到各个组织,具有广泛、持久的特点。其调控流程如图 4所示,作用变化规律与式(1) 相似,仅其中参数取值不同。
|
| 图 4 内分泌调控机制示意图 Fig.4 Diagram of endocrine regulation mechanism |
人工蜂群算法通常用于解决函数优化、方案优化等问题,依据自然界中的蜜蜂种群结构设定3种角色:引领蜂(雇佣蜂)、跟随蜂(观察蜂)和侦查蜂,主要行为有两种:发现蜜源和放弃蜜源[15-16]。在待解决的问题中,蜜源代表优化问题的可行解,其优劣信息被引领蜂一对一记录,首先有记忆功能的引领蜂会在空间内寻找食物源,回到蜂巢后在招募区跳摇摆舞,将蜜源信息以一定概率传递给观察蜂,观察蜂是蜂巢附近等待引领蜂分享蜜源的蜜蜂,它们观察引领蜂的舞蹈并择优跟随,观察蜂可以接受引领蜂提供的信息,并跟随引领蜂一起去采蜜,也可以不接受信息,转而变成新的引领蜂去寻找蜜源,此过程中记录最好的蜜源位置。引领蜂在蜂巢周围继续搜索附近新蜜源,若一个蜜源达到指定迭代次数后没有被更新,则引领蜂转变为侦查蜂,放弃该蜜源转而去寻找新的蜜源,开始新一轮迭代,直到满足结束条件后输出最优蜜源。
人工蜂群算法中最大的特点就是角色分工,同时各类蜜蜂之间均可进行角色转换。其算法步骤大致可分为初始化、引领蜂记录蜜源信息、跟随蜂采蜜、产生侦查蜂这几个步骤[17]。传统的人工蜂群算法具有控制参数少,鲁棒性强等诸多优点,也存在易于早熟等缺点,用于解决非线性多参数问题还存在较大的误差。同时,部分经过改进后的人工蜂群算法还停留在易于陷入局部最优的阶段,优化效果有待进一步改进。
2 基于生物调节机制的ABC算法原理为解决传统人工蜂群算法应用于实际问题时所存在诸多缺陷,受生物系统调控生理指标机制的启发,提出一种NEI-ABC智能算法。该算法在原有算法引领蜂、观察蜂、侦查蜂的基础上,根据生物机制调节规律设计了蓝光引导单元、蜜源调控单元和触角定向单元。其中,蓝光引导单元是依据神经引导机制的作用机理设计的,模拟蜜蜂采蜜时“蓝光”对其导向作用而提出,作用于跟随蜂阶段,能够加强算法跳出局部最优的能力;触角定向单元是依据免疫定向机制作用机理设计的,来源于蜜蜂生理结构上触角的实际作用,作用于侦查蜂阶段,能够在一定程度上增大精细寻优能力,加快算法的收敛速度;蜜源调控单元是根据内分泌调控机制作用原理提出的,结合蜜蜂工作过程中采蜜效率变化的生物背景,作用于引领蜂阶段,能够有效缩短算法的执行时间。新引入各个单元与人工蜂群算法、生物背景之间对应关系可表述如表 1所示。
| 单元名称 | 生物机制 | 生物背景 | 优化作用 |
| 蓝光引导单元 | 神经引导机制 | 蓝光对蜜蜂的导向作用 | 扩大搜索范围 |
| 触角定向单元 | 免疫定向机制 | 蜜蜂触角的定向作用 | 定向局部寻优 |
| 蜜源调控单元 | 内分泌调控机制 | 蜜蜂采蜜效率变化规律 | 减少算法执行时间 |
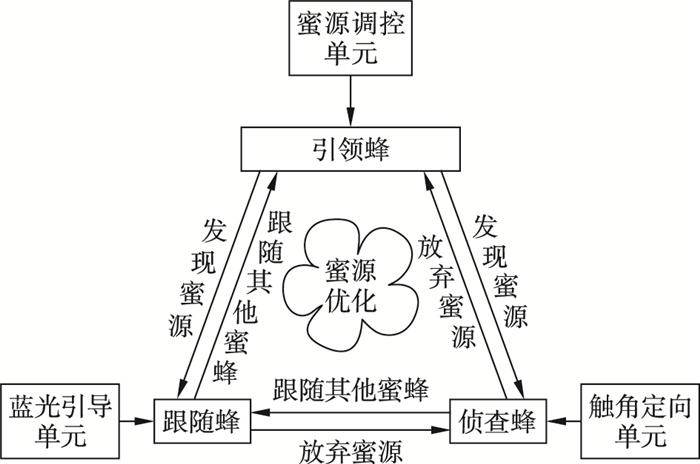
利用上述设计思想对跟随蜂、侦查蜂、引领蜂的采蜜机理进行改进,更接近实际蜂群采蜜过程,可提高全局搜索能力,有效提高算法收敛速度并改善运行效果。NEI-ABC算法组成架构如图 5所示。
|
| 图 5 NEI-ABC算法架构 Fig.5 NEI-ABC algorithm architecture |
传统人工蜂群算法中,跟随蜂在跟随采蜜时具有较强的随机性,使算法收敛速度相对较慢。而自然界中,花朵能散发出人眼看不到的“蓝色光环”,对蜜蜂有很强的吸引作用,在“蓝光”的引导下,蜜蜂可找到花朵进行蜜源开采。受人体内存在的神经引导机制启发,本文在传统人工蜂群算法中加入蓝光引导单元,以提高解的多样性,增强全局寻优能力,其具体原理设计如下。
在传统人工蜂群算法中,引领蜂在确定完初始蜜源位置后,回到蜂巢向跟随蜂传递信息,跟随蜂有跟随引领蜂采蜜和不跟随引领蜂采蜜两种选择,不跟随的跟随蜂将会变成新的引领蜂,在解空间中展开新的搜索流程,此搜索过程中根据式(2)产生新蜜源,此搜索策略与引领蜂相同:
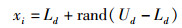
|
(2) |
式中,Ld和Ud分别为表示蜜蜂搜索空间的上限和下限,d=1,2,…,D,D为待求解问题的维数;rand函数在区间[0, 1]内产生随机数。由于此搜寻方式容易产生重复解,这使传统ABC算法寻优过程中极易陷入局部最优值。
为克服上述缺陷,在蓝光引导单元中引入基于神经引导机制设计的“蓝光引导因子”,其搜索规律如式(3)所示:
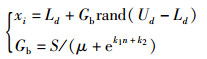
|
(3) |
式中,Gb为引导作用函数;S用于调节引导作用的强弱,μ为固定常数,并且S>0,μ>0;k1、k2为蓝光引导系统参数,k1>0,k2 < 0。迭代次数n从第一次迭代开始逐渐变化,加入蓝光引导单元后增大了蜜蜂搜索范围,可使算法全局寻优能力得到提升。
在人工蜂群算法中引入蓝光引导单元,计算新蜜源的适应度值并进行贪婪选择,能够在一定程度上避免与引领蜂在同一位置产生新蜜源,提高了全局搜索能力。
2.2 蜜源调控单元设计传统人工蜂群算法在解决优化问题时存在执行时间较长的问题,同时实验研究表明长时间的工作会使蜜蜂的工作效率有所降低。受人体内存在的内分泌调控机制的启发,本文在传统人工蜂群算法中加入蜜源调控单元,以减少算法的执行时间,其具体原理设计如下。
在传统人工蜂群算法中,当前最优蜜源被记录后,对其他蜜源的搜索仍在进行,如果某蜜源xi经过n次迭代搜索到达阈值而没有找到更好的解,该蜜源xi被抛弃,引领蜂转化为侦查蜂并继续搜寻新的蜜源来代替xi,如式(4)所示。
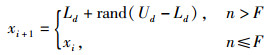
|
(4) |
式中,n为迭代次数,F为阈值。由于此过程中对任一蜜源的迭代次数相同,使搜索耗时增加。
为克服上述缺陷,基于内分泌调控机制,在蜜源调控单元中增加参数调控因子作用于侦查蜂并对迭代次数n进行界定,具体如式(5)所示。
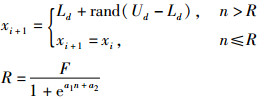
|
(5) |
式中,R为调控激素的浓度变化量;F为阈值(固定常数);a1、a2为蜜源调控单元系统参数,a1>0,a2 < 0;Ld和Ud含义同式(2)。加入蜜源调控单元后,可使侦查蜂迭代次数随采蜜时间的增长而减小,有效减少算法执行所需时间。
2.3 触角定向单元设计蜜蜂的触角能给蜜蜂带来触觉和嗅觉,触觉用来识别风速、气压等飞行条件,嗅觉用来帮助蜜蜂辨别敌友、识别各种花的香味,然后找到自己喜欢的花朵来采蜜。受人体内免疫定向机制的启发,在传统人工蜂群算法中引入触角定向单元,以提高算法收敛速度,具体原理设计如下。
传统人工蜂群算法中,侦查蜂产生新蜜源时直接根据式(2)在空间内随机产生一个新蜜源。这种方式具有极大的不确定性,增加了算法运行的时间复杂度,不利于快速收敛到最优值。
为了克服上述问题,基于免疫定向机制在触角定向单元中引入定位因子,将侦查蜂的搜索点定义到当前全局最优位置,设计的触角定向单元公式如式(6)所示。
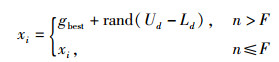
|
(6) |
式中,gbest为当前全局最优位置,n为迭代次数。
引入触角定向单元后,以侦查蜂在蜂巢附近搜索蜜源为原型,将侦查蜂搜索蜜源的中心点通过定位因子定位到当前全局最优位置,可增加侦查蜂在最优点附近的局部搜索概率,能够在一定程度上加快算法的收敛速度。
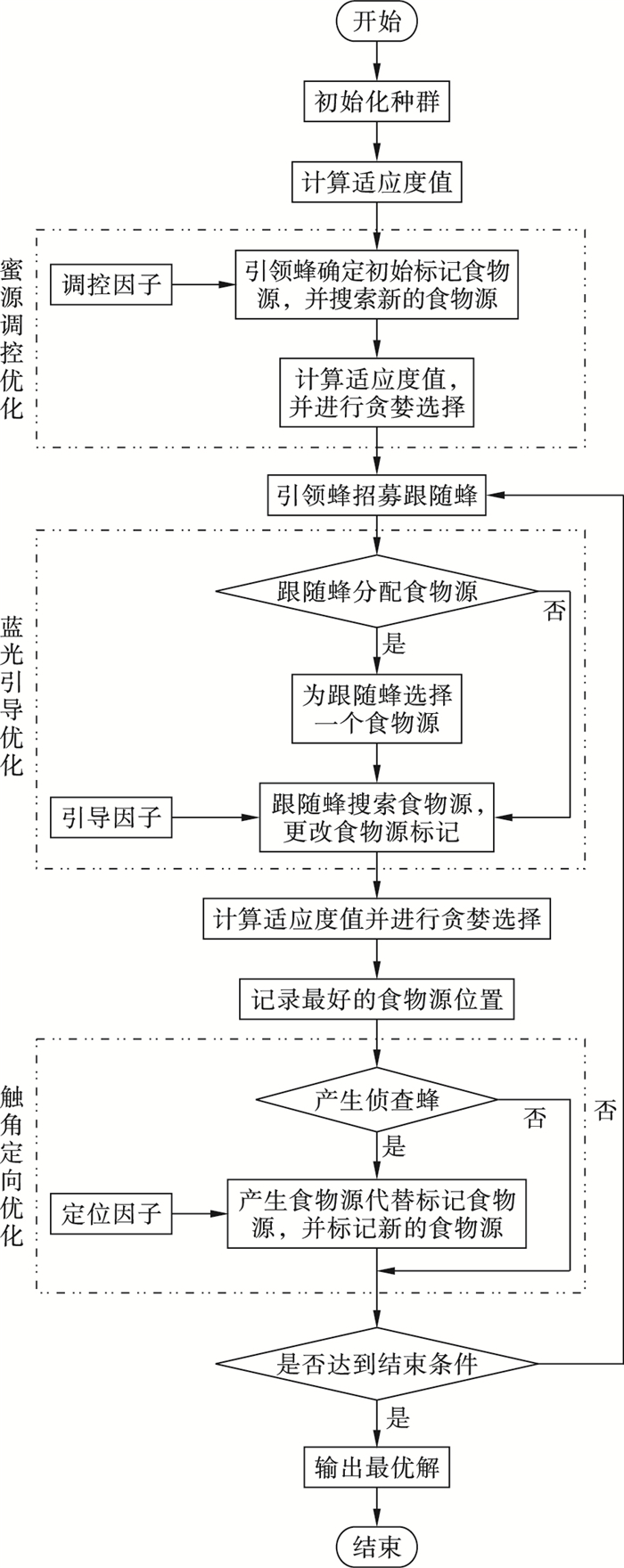
2.4 NEI-ABC算法实现NEI-ABC智能算法步骤如下,算法流程如图 6所示。
|
| 图 6 NEI-ABC算法流程图 Fig.6 NEI-ABC algorithm flow chart |
1) 蜜源初始化。蜜源进行随机初始化,引领蜂确定初始标记蜜源并搜索新蜜源,计算适应度值,并进行贪婪选择。蜜源i(i=1,2,…,N)的质量对应于解的适应度值ξi,N为蜜源的数量,假设待求解问题的维数为D,在n次迭代时蜜源i的位置可以表示为xin=[xi1n,xi2n,…,xiDn],其中,xid∈[Ld,Ud),Ld和Ud分别为搜索空间的上限和下限,d=1,2,…,D。
2) 跟随蜂选择引领蜂的概率。对于引领蜂的所提供的蜜源信息,跟随蜂按照式(7)得到跟随的概率。
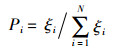
|
(7) |
式中,ξi为当前解的适应度函数值。
不跟随引领蜂采蜜的跟随蜂将会变成引领蜂,在解空间中继续搜索新蜜源,传统ABC算法产生新蜜源的公式如式(2)所示,引入蓝光引导单元后其搜索公式如式(3)所示,计算新蜜源的适应度值并进行贪婪选择。
3) 新蜜源的搜索公式。引领蜂在招募区招募跟随蜂后,会在蜜源的周围根据式(8)继续搜索得到新蜜源。
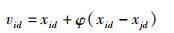
|
(8) |
式中,j∈{1,2,…,N}且j≠i,φ为[-1,1]均匀分布的扰动因子,当蜜源vi的适应度优于xi时,选取新蜜源代替原来的蜜源,否则保留xi。所有的引领蜂完成式(8)的运算后,共同分享信息。
4) 产生侦查蜂。经过有限次数迭代而蜜源未进行更新,则产生侦查蜂,NEI-ABC算法中侦查蜂产生方式如式(5)所示。
5) 算法迭代寻优直到满足结束条件。
2.5 NEI-ABC算法稳定性能分析 2.5.1 NEI-ABC算法收敛性分析本文中依据文[18]利用马尔可夫链理论验证ABC算法收敛性的方式,将NEI-ABC算法各项参数转化为马尔可夫链参数值,对其运算过程做全局收敛性分析。
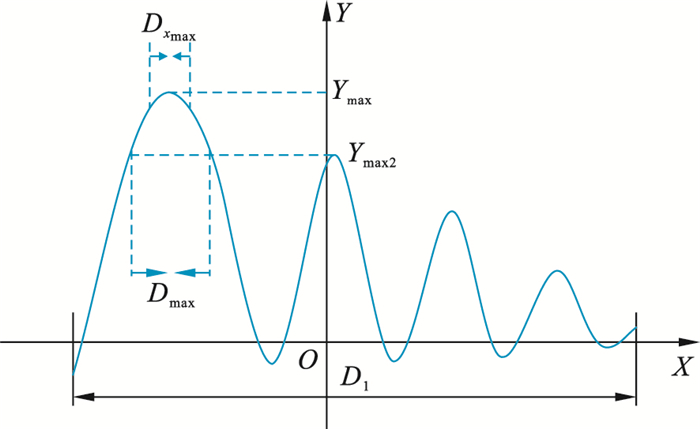
假设图 7为函数值变化曲线,D1为自变量的取值范围,区间范围为d1,设Ymax是该函数的最大值,Ymax2值的大小仅次于Ymax,Dmax是函数值位于[Ymax2,Ymax]内时自变量的取值范围,称为最优区域,区间范围为dmax;Dxmax是近似最大值选取的小段范围,在区域(xmax-ε,xmax+ε)内,记为全局最优,长度记为2ε。
|
| 图 7 NEI-ABC算法收敛性分析 Fig.7 Convergence analysis of NEI-ABC algorithm |
当NEI-ABC算法开始运行时,初始化蜜源位置,对应的蜜蜂落在Dmax区域内的概率为
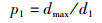
|
(9) |
此概率服从正态分布。
在新蜜源的产生式(2)中,φ∈[-1, 1],可得
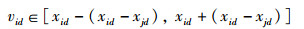
|
(10) |
将此区域范围记作Dik,此范围内vid优于xid的位置。在Dik区域范围内,将适应度值大于xid的点的集合记为Di→d,蜜源位置更新的概率为
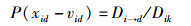
|
(11) |
即蜜源的更新公式服从均匀分布。新蜜源的产生落在Dik范围内的概率也服从均匀分布。
在算法的迭代过程中,蜜蜂从当前状态xi一步转移至某一状态xj的概率记为P(xi→xj),因为式(11)服从均匀分布,所以xi从长度为L的取值范围更新至另一长度为L1取值范围的概率同样也服从均匀分布,即:
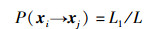
|
(12) |
第一次蜜蜂初始化后,大多数的蜜蜂都是随机地分布在D区域内,之后开始每一次迭代,对于当前位置xi和下一个任意位置xk的转移范围Dik和Dmax之间的关系可划分为相交、包含、相离、包含于4种关系。
记Dik的长度为dik,Dik与Dmax的相交长度为d∩ik,迭代过程中蜜蜂一步移动到Dmax区域的概率为
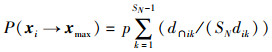
|
(13) |
式中,SN为种群大小,p是选择蜜源的概率,dik恒大于0。对任意蜜蜂xi,经过迭代后必然可以转移到Dmax区域内的概率为1-P(xi→xmax)。可求得
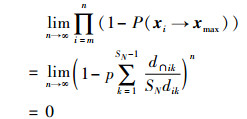
|
(14) |
当蜜蜂状态xi经过有限次迭代后转变为侦查蜂,可得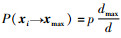
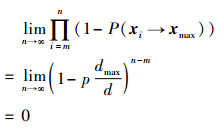
|
(15) |
即经过n次迭代,蜜蜂的位置必然转移到Dmax区域内。
当假设处于极小概率的Dik和Dmax之间为相离时,NEI-ABC算法会陷入局部最优,两区域没有交叉点,蜂群无法转移到Dmax所在区域,即1-P(xi→xmax)=1。此时蜜蜂状态xi无法转移到Dmax的概率为
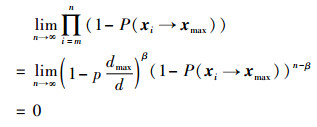
|
(16) |
明显与假设不符,所以假设不成立。因此,蜜蜂的位置必然转移至Dmax区域内进行迭代贪心选择,即算法收敛。
2.5.2 NEI-ABC算法稳定性分析由2.5.1节可知,NEI-ABC算法能够收敛于全局最优点,因此假设李雅普诺夫意义下的平衡点为全局最优点xmax。
设该算法的目标函数为f(x),其动态方程为
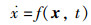
|
(17) |
把坐标函数迁移,令X轴向上迁移‖xmax‖,可得到NEI-ABC算法动态方程:
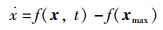
|
(18) |
由2.5.1节算法收敛性可知,当t→∞时,x趋于全局最优位置xmax,即:
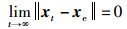
|
(19) |
则xe为平衡点,f(xmax,t)为平衡状态。
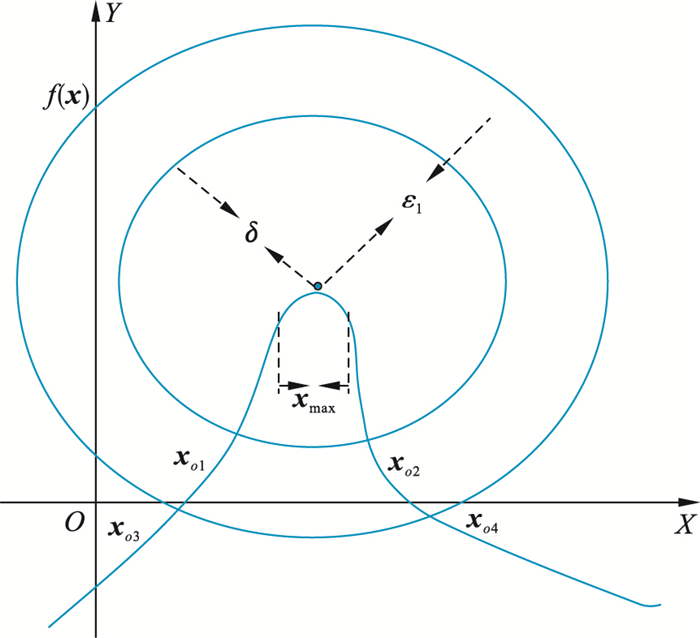
假设NEI-ABC算法的初始状态位于以平衡状态xmax为圆心,δ为半径的圆s(δ)内,即‖x0-xmax‖≤δ,如图 8所示,s(δ)和s(ε)分别是以xmax为圆心,以δ和ε为半径的同心圆,s(ε)与f(x)相交于点xo3、xo4,Dmax为最优区域,xo1、xo2为该最优区域的范围。由算法收敛性可知,Dmax区域内的蜜蜂状态xi会一直朝着最优位置xmax逼近,因此只要方程的初始解位于Dmax区域内,xi就会一直朝着xmax方向前进,不会落在半径为δ的圆的范围之外。
|
| 图 8 NEI-ABC算法稳定性分析 Fig.8 Stability analysis of NEI-ABC algorithm |
从图 8中分析可得
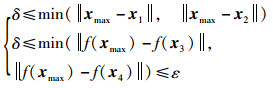
|
(20) |
可得
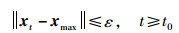
|
(21) |
即当t→∞时,xt都位于圆s(ε)内。因此当圆s(δ)与目标函数相交的区域包含于Dmax时,NEI-ABC算法的平衡状态在李雅普诺夫意义下是稳定的。对于任意实数ε>0,总存在实数δ,当xt的任一初始状态满足‖x0-xmax‖≤δ时,xt满足:
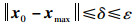
|
(22) |
即xt始终在圆s(δ)内,与半径δ和初始时间无关。所以NEI-ABC算法在李雅普诺夫意义下是稳定的。
3 NEI-ABC算法验证及应用 3.1 NEI-ABC算法性能验证为测试NEI-ABC算法性能,本文在Matlab实验环境中选取文[19]所提Benchmark函数进行仿真验证。已知函数最优值均为0,维度设置D=30,xi∈[-10, 10],最大迭代次数设为500代(粒子群优化算法中,种群大小设置为2 000,个体项学习因子和群体项学习因子均设置为2;ABC、多邻域搜索人工蜂群算法(multi neighborhood search artificial bee colony algorithm,MN-ABC)、NEI-ABC的种群大小均设置为200),算法中相关变量的取值如表 2所示,相关函数表达式如表 3所示。
| 变量 | 变量取值 | 变量 | 变量取值 | |
| S | 1 | a1 | 10 | |
| μ | 1 | a2 | -5 | |
| k1 | 20 | Ld | -1 | |
| k2 | -10 | Ud | 1 | |
| F | 50 |
| 函数名称 | 表达式 |
| Griewank | 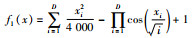 |
| Ackley | 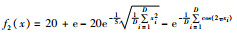 |
| Rastrigrin | 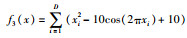 |
| Schewefel | 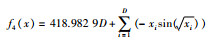 |
| Rosenbrock | 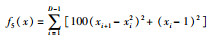 |
| Sumsquares | 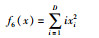 |
| Dixon-price | 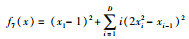 |
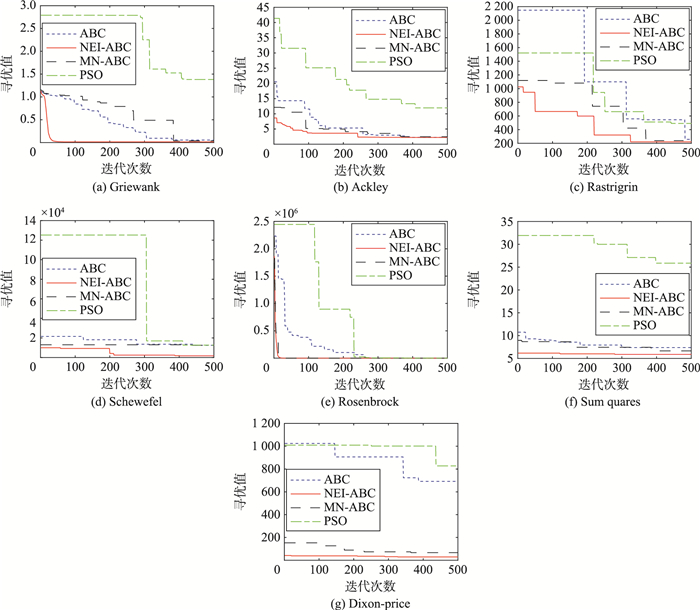
4种算法运行后的仿真实验结果如图 9所示,7个函数的详细对比数据见表 4。
|
| 图 9 Benchmark函数运行效果图 Fig.9 Benchmark function running effect |
| 函数名称 | 算法名称 | 迭代次数 | 最优值 |
| Griewank | NEI-ABC | 168 | 1.529×10-1 |
| ABC | 398 | 5.521×10-1 | |
| MN-ABC | 384 | 3.668×10-1 | |
| PSO | 422 | 1.383×100 | |
| Ackley | NEI-ABC | 262 | 2.204×100 |
| ABC | 398 | 2.452×100 | |
| MN-ABC | 396 | 2.252×100 | |
| PSO | 408 | 1.194×101 | |
| Rastrigrin | NEI-ABC | 325 | 2.215×102 |
| ABC | 482 | 2.581×102 | |
| MN-ABC | 392 | 2.396×102 | |
| PSO | 442 | 4.907×103 | |
| Schewefel | NEI-ABC | 402 | 1.716×104 |
| ABC | 446 | 1.245×105 | |
| MN-ABC | 418 | 1.245×105 | |
| PSO | 500 | 1.245×105 | |
| Rosenbrock | NEI-ABC | 277 | 3.152×101 |
| ABC | 297 | 1.913×103 | |
| MN-ABC | 279 | 1.731×103 | |
| PSO | 452 | 7.751×103 | |
| Sumsquares | NEI-ABC | 280 | 5.872×100 |
| ABC | 385 | 7.373×100 | |
| MN-ABC | 300 | 6.651×100 | |
| PSO | 398 | 2.587×101 | |
| Dixon-price | NEI-ABC | 327 | 2.939×101 |
| ABC | 387 | 6.917×102 | |
| MN-ABC | 365 | 6.679×101 | |
| PSO | 437 | 8.269×102 |
图 9(a)~图 9(g)分别为Griewank、Ackley、Rastrigrin、Schewefel、Rosenbrock、Sum squares和Dixon-price函数的优化效果图。在优化过程中,NEI-ABC相对其他3种算法迭代次数最高分别减少60. 2%、35. 8%、32. 6%、19. 6%、38. 6%、29. 6%、25. 2%;其寻优精度相对其他3种算法分别提升98. 9%、81. 6%、54. 9%、86. 3%、95. 9%、77. 3%、96. 4%。通过上述检验,可以发现NEI-ABC算法的收敛速度和优化精度相对表现最好,具体参见表 4中相关数据结果。
3.2 基于NEI-ABC算法在油田注采优化决策我国是能源消耗大国,目前大部分油田的产量呈下降趋势,应用传统注采优化方案时收敛速度慢、易于早熟等问题日渐凸显。因此,对原油开采工作做出合理优化,有利于减少自然资源的浪费,延长油田使用寿命。油田开采的过程中,衡量其经济效益的指标不能仅仅为单一的注水量或者采出量,以经济效益为指标进行优化,具有重要意义[20]。
在所采集的数据中,注水量、采油量可通过4口注水井的注水量来建立相关评价函数,将变量归一化到[-1, 1]之间,采用小波神经网络构建得到注入与产出模型函数:
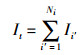
|
(23) |
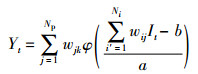
|
(24) |
式中,wij、wjk为小波神经网络权值参数,a为伸缩因子,b为平移因子,φ为激活函数,It为每日注入总量(单位:t/d),Yt为油田日产量(单位:t/d),且Ii∈[0, 120](单位:t/d),Np为生产井总数,Ni为注水井总数。
本文综合考虑注水与采出对油田经济效益所带来的对立关系,依据某油田区块4口注水井与其对应的一口采油井的注采生产数据,建立如式(25)所示的原油日净现值优化方程。
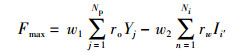
|
(25) |
式中,Yj为第j口生产井日产量,ro为原油价格(单位:元),Np为生产井总数,Ii′为第i′口井的实际注入量,rw为单位注水成本价格(单位:元),Ni为注水井总数。w1与w2分别代表注入与采出所占权重比,且w1+w2=1,依据实际油田常规调整情况设置参数w1=0. 6,w2=0. 4,实际情况中该值可依据工况条件再作调整,通过优化注水参数得到最优注采效果。
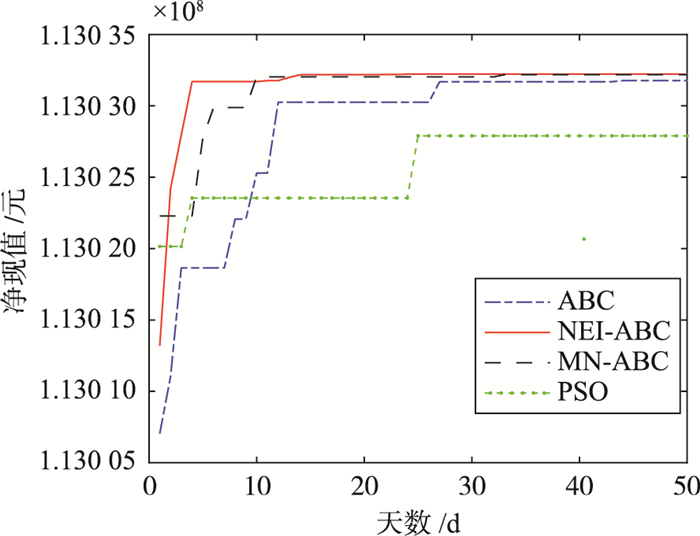
采用4种算法优化后的油田产量对比结果如图 10所示,相关数据对比见表 5。
|
| 图 10 油田产量优化效果对比图 Fig.10 Comparison chart of output optimization effect in odfield |
| 函数 | 运行状况 | |
| 最优代数 | 最优值/元 | |
| ABC | 27 | 113 031 765.05 |
| PSO | 25 | 113 027 900.24 |
| MN-ABC | 33 | 113 031 977.03 |
| NEI-ABC | 24 | 113 032 220.44 |
从图 10和表 5中分析可以得出,人工蜂群算法在第27代可达到最优,其值为113 031 765. 05元,粒子群优化算法在第25代可达到最优,其值为113 027 900. 24元,MN-ABC算法在33代可达到最优,其值为113 032 277. 03元,NEI-ABC算法在第24代可达到最优,其值为113 032 220. 44元。由于相对本文所选高维测试函数,油田日产值优化函数的参数维度相对较少,所以寻优精度相差较小,但NEI-ABC算法寻优效果相对其他算法均有所提升。
由结果分析可知,在当前工况条件下,4口井每天的注水量分别为51. 7 t/d、59. 4 t/d、118. 8 t/d、118. 8 t/d时,注水效率最高,每日净现值为113 032 220. 44元,可达到最优。根据采集数据显示,目前工况条件下日净现值约为104 075 900. 1元,经过NEI-ABC智能算法优化后的日净现值提高8. 61%。油田生产理论最优值很难计算获得,原则上在不破坏地层环境的前提下,以提升经济效益为目的,优化后的产量越大越好。因此,NEI-ABC算法能够有效提高原油生产日净现值,为注采规划等复杂多参数问题的解决提供新途径。
4 结论本文结合人体内存在的生物调节机制,对人工蜂群算法进行改进,提出一种NEI-ABC智能算法。在传统人工蜂群算法中加入蓝光引导单元、蜜源调控单元、触角定向单元,通过扩大搜索范围、调控迭代次数、定向局部寻优等措施可有效缩短算法收敛所需时间,加快收敛速度,提高全局寻优能力。将此算法应用于油田开采的工况条件配置中,能得到合理的产量规划方案,有效减少自然资源的浪费,有利于工况条件的合理配置,此方法可为多参数问题的优化方案带来一定的参考。
本文所设计的NEI-ABC智能规划算法具备精度高、收敛快的优点,但此算法是基于单种群设计的,未来可在多种群协同进化方向上得到进一步提高。
| [1] |
GAO H, FU Z, PUN C M, et al. An efficient artificial bee colony algorithm with an improved linkage identification method[J]. IEEE Transactions on Cybernetics, 2022, 52(6): 4400-4414. DOI:10.1109/TCYB.2020.3026716 |
| [2] |
WANG L, ZHANG X, ZHANG X. Antenna array design by artificial bee colony algorithm with similarity induced search method[J/OL]. IEEE Transactions on Magnetics, 2019, 55(6)[2021-12-16]. https://ieeexplore.ieee.org/document/8653485/citations#citations. DOI: 10.1109/TMAG.2019.2896921.
|
| [3] |
LI J Q, SONG M X, WANG L, et al. Hybrid artificial bee colony algorithm for a parallel batching distributed flow-shop problem with deteriorating jobs[J]. IEEE Transactions on Cybernetics, 2020, 50(6): 2425-2439. DOI:10.1109/TCYB.2019.2943606 |
| [4] |
DING Y, XU N, DAI S, et al. An immune system-inspired reconfigurable controller[J]. IEEE Transactions on Control Systems Technology, 2016, 24(5): 1875-1882. DOI:10.1109/TCST.2016.2514847 |
| [5] |
刘刚, 黄崇争. 基于HDABC算法的置换流水车间调度策略[J]. 控制工程, 2017, 24(9): 1925-1929. LIU G, HUANG C Z. Replacement flow shop scheduling strategy based on hdabc algorithm[J]. Control Engineering, 2017, 24(9): 1925-1929. DOI:10.14107/j.cnki.kzgc.150408 |
| [6] |
叶奕茂, 赵华生, 金龙. 一种基于PSO-ABC的全局优化算法[J]. 广西民族大学学报(自然科学版), 2013, 19(4): 55-59. YE Y M, ZHAO H S, JIN L. A global optimization algorithm based on PSO-ABC[J]. Journal of Guangxi University for Nationalities (Natural Science Edition), 2013, 19(4): 55-59. DOI:10.3969/j.issn.1673-8462.2013.04.010 |
| [7] |
蒋伟, 陈照光. 基于改进的人工蜂群算法的微电网储能系统容量优化配置[J]. 上海电力大学学报, 2021, 37(5): 415-421, 427. JIANG W, CHEN Z G. Optimal capacity allocation of microgrid energy storage system based on improved artificial bee colony algorithm[J]. Journal of Shanghai Electric Power University, 2021, 37(5): 415-421, 427. DOI:10.3969/j.issn.2096-8299.2021.05.001 |
| [8] |
李宏娟, 徐格宁, 姚艳萍. 基于改进型ABC算法的异步电机参数估计方法[J]. 控制工程, 2018, 25(3): 436-441. LI H J, XU G N, YAO Y P. Parameter estimation method of asynchronous motor based on improved ABC algorithm[J]. Control Engineering, 2018, 25(3): 436-441. |
| [9] |
管雪梅, 黄青龙, 黄靖一, 等. 基于改进人工蜂群算法的大青杨晚材率预测[J]. 科学技术与工程, 2021, 21(26): 11118-11124. GUAN X M, HUANG Q L, HUANG J Y, et al. Prediction of latewood rate of Populus euphratica based on improved artificial bee colony algorithm[J]. Science, Technology and Engineering, 2021, 21(26): 11118-11124. DOI:10.3969/j.issn.1671-1815.2021.26.015 |
| [10] |
VIEIRA R, ARGENTO E, REVOREDO T. Trajectory Planning for car-like robots through curve parametrization and genetic algorithm optimization with applications to autonomous parking[J]. IEEE Latin America Transactions, 2022, 20(2): 309-316. DOI:10.1109/TLA.2022.9661471 |
| [11] |
李六柯, 张则强, 邹宾森, 等. 免疫机制协作遗传算法的多目标拆卸线平衡优化[J]. 信息与控制, 2018, 47(6): 671-679. LI L K, ZHANG Z Q, ZOU B S, et al. Multi-objective immune balance of disassembly genetic algorithm[J]. Information and Control, 2018, 47(6): 671-679. |
| [12] |
刘宝, 丁永生, 王君红. 基于NEI调节机制的非线性智能优化控制器[J]. 控制与决策, 2008, 23(10): 1159-1162. LIU B, DING Y S, WANG J H. Nonlinear intelligent optimization controller based on NEI regulation mechanism[J]. Control and Decision, 2008, 23(10): 1159-1162. DOI:10.3321/j.issn:1001-0920.2008.10.016 |
| [13] |
CORUS D, OLIVETO P S, YAZDANI D. Fast immune system-inspired hypermutation operators for combinatorial optimization[J]. IEEE Transactions on Evolutionary Computation, 2021, 25(5): 956-970. DOI:10.1109/TEVC.2021.3068574 |
| [14] |
YANG Z, DING Y, JIN Y, et al. Immune-endocrine system inspired hierarchical coevolutionary multiobjective optimization algorithm for IoT service[J]. IEEE Transactions on Cybernetics, 2020, 50(1): 164-177. DOI:10.1109/TCYB.2018.2866527 |
| [15] |
CALISKAN A, ÇIL Z A, BADEM H, et al. Regression-based neuro-fuzzy network trained by ABC algorithm for high-density impulse noise elimination[J]. IEEE Transactions on Fuzzy Systems, 2020, 28(6): 1084-1095. DOI:10.1109/TFUZZ.2020.2973123 |
| [16] |
YANG L, SUN X, PENG L, et al. An agent-based artificial bee colony (ABC) algorithm for hyperspectral image endmember extraction in parallel[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(10): 4657-4664. DOI:10.1109/JSTARS.2015.2454518 |
| [17] |
宋晓宇, 张卿, 常春光. 求解双层应急物资调度的改进蜂群算法[J]. 信息与控制, 2015, 44(6): 729-738. SONG X Y, ZHANG Q, CHANG C G. Improved bee colony algorithm for solving double-layer emergency material scheduling[J]. Information and Control, 2015, 44(6): 729-738. |
| [18] |
王野. 人工蜂群算法收敛性和稳定性分析[D]. 兰州: 兰州交通大学, 2018. WANG Y. Convergence and stability analysis of artificial bee colony algorithm[D]. Lanzhou: Lanzhou Jiaotong University, 2018. |
| [19] |
LIU L, SHAN L, DAI Y W, et al. Improved quantum bacterial foraging algorithm for tuning parameters of fractional-order PID controller[J]. Journal of Systems Engineering and Electronics, 2018, 29(1): 166-175. |
| [20] |
ZHANG Z X, XU Q S, JIANG M F, et al. The application of optimum decision in oilfield development[J]. Journal of Systems Engineering and Electronics, 2000, 11(2): 5-10. |



