0 引言
随着中国提出力争在2030年和2060年之前分别实现“碳达峰”和“碳中和”的双碳目标推进[1],大力推动新能源技术发展已然是必然选择,风电作为绿色清洁能源之一,发展迅猛。然而风电出力易受气象特征及设备运行等多种因素影响,使得发电功率具有强随机性和非平稳性,并网时会对电力系统的安全稳定造成巨大影响。因此,为提升风电的消纳能力,维护电力系统安全稳定,准确有效的风电功率预测显得尤为重要[2]。
目前,常用的风电功率预测方法主要包括物理法和统计法两大类[3]。物理法通常需要考虑数值天气预报(numerical weather prediction,NWP)数据信息[4]、风电场地形地貌信息[5]、风电机组信息[6],通过求解复杂的偏微分方程组进行预测。统计法主要通过算法学习建立影响因素与风电功率间的非线性联系,然后结合NWP数据和实测数据进行预测。统计法不仅包括持续法[7]、自回归差分移动平均[8]等时间序列法;支持向量回归(support vector regression,SVR)[9]、随机森林[10]等传统机器学习方法;还包括长短期记忆网络[11-12]、门控循环单元[13-14]、反向传播(back propagation,BP)网络[15]和极限学习机(extreme learning machine,ELM)[16]等深度学习算法。但由于风电功率波动性强、非平稳性高的特点,使得单一预测算法并不能充分学习功率与特征影响因素间的非线性关系。不少学者通过使用一些信号处理方法,对功率分解后再进行建模预测,为提高风电功率预测精度奠定了数据基础。文[17]采用集成经验模态分解(ensemble empirical mode decomposition,EEMD)与改进核极限学习机(kernel extreme learning machine,KELM)的预测模型,提高了预测精度,并且EEMD缓解了经验模态分解[18]的模态混叠,但其残留噪声也会削弱数据序列中的有效信息影响预测精度。文[19]提出了一种自适应噪声完整集成经验模态分解加模糊熵重构及核极限学习机的预测方法,该分解方法很好地解决了模态混叠及残留噪声的影响,取得了较好的预测精度,但该分解方法也会由于集合平均时产生误差而影响精度。文[20]通过将VMD分解后的分量,划分为3种趋势分量,再分别进行预测,减少了建模数量,提高了模型的预测效率和精度。VMD虽有效克服了经验模态分解的缺点,但模态数量及一些关键参数仍需手动设置,自适应性较差,且手动调参具有较大的分解随机性。基于此,文[21]提出了一种基于最优VMD及改进深度极限学习机的风电功率预测模型,通过观察中心频率的方法确定模态数K,有效避免了VMD的过分解及欠分解,且优化的深度极限学习机模型有效提高了预测精度。文[22]提出了一种基于自适应变分模态分解的风功率组合预测方法,通过使用一种结合了排列熵的信号随机性检测方法,确定了VMD的K值。两种方法都仅对模态数量K作了选取,惩罚因子α值仍然通过人工经验方式选取,但α值对VMD分解的影响也尤为重要。文[23]提出了一种基于优化算法寻优VMD关键参数及小波核极限学习机的风电功率多步预测方法,通过将各分量排列熵加权设计适应度函数,在提高VMD分解自适应的同时对最优解求解提供了有效判别。在众多预测算法中,核极限学习机以其训练速度快、学习能力强、无需设定隐含层节点数、训练结果稳定等特点,得到了广泛应用。但采用单一核函数的核极限学习机,往往难以兼顾学习精度和泛化能力,同时也难以适应风电功率这种多数据特征样本[24]。
基于上述,本文提出了一种基于SSA优化VMD-HKELM的短期风电功率预测方法。首先,使用SSA优化VMD(optimized VMD,OVMD)将风电功率分解为一组平稳子分量,基于排列熵、Pearson相关系数和VMD迭代代数构建综合指标,作为SSA优化VMD参数的适应度函数,以实现VMD对风电功率的自适应分解。然后,使用混合核函数代替单一核函数,对各分量结合气象特征分别建立兼顾学习与泛化能力的HKELM预测模型,同时利用SSA对模型参数寻优。最后,迭加各分量的预测值,得到最终预测值。与多种方法进行实验对比,结果表明本文方法具有更好的预测精度与泛化性。
1 方法与理论 1.1 变分模态分解VMD在检测分解非线性、非平稳信号方面具有良好的性能。可将风电功率信号f(t)分解为K个不同的本征模态函数(intrinsic mode function,IMF)分量uk及对应中心频率ωk,其分解可概括为变分问题的构建和求解过程,步骤如下:
1) 对每个uk通过希尔伯特变换得到单边频谱及解析信号,将解析信号及其预估中心频率e-jωkt项混合,把频谱变换到基带上,利用高斯平滑估算已解调信号的带宽,并构建变分约束问题如下:
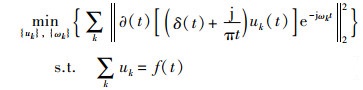
|
(1) |
2) 使用拉格朗日算子λ(t)和二次惩罚因子α,将变分约束问题转变为非约束问题,求解变分问题最优解:
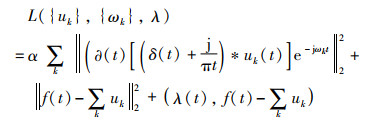
|
(2) |
3) 通过交替方向乘子法实现对uk及ωk的交替更新,完成VMD分解。
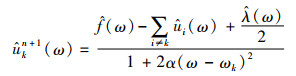
|
(3) |
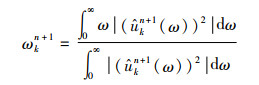
|
(4) |
式中,n为迭代次数,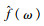
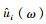
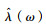
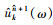
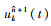
SSA算法是2020年由XUE等[25]受麻雀捕食行为启发而提出的一种新型群智能优化算法,麻雀种群按其职能行为可划分为发现者和追随者。
发现者是种群中适应度较好的个体,负责搜索食物源,同时为追随者提供食物源的位置,一般占10%~20%,位置更新公式如式(5):
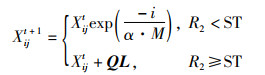
|
(5) |
式中:t表示当前迭代次数,Xijt表示第i个麻雀在第j维的位置,M表示最大迭代次数,α∈(0,1]的随机数,Q为服从正态分布的随机数,R2∈[0, 1]和ST∈[0.5,1]分别为预警值和安全值,L为值均为1的1×j矩阵。
剩余个体为紧跟发现者进行觅食行为的追随者,位置更新公式如式(6):
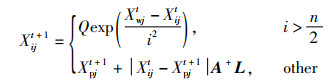
|
(6) |
式中,Xpj表示t+1次迭代最优位置,Xwj表示t次迭代全局最差位置,A为值为-1或1的1×j矩阵,且A+=AT(AAT)-1。
同时,每代会随机分配10%~20%的警戒者,巡查监控觅食区域,当遇到危险时会发出报警信号,并迅速向安全地点转移,从而避免被捕食,位置更新公式如下:
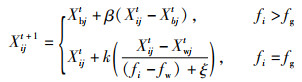
|
(7) |
式中,Xbj表示全局最佳位置,β是步长控制参数,k∈[-1, 1]的均匀随机数,ξ是极小实数,fg和fw分别表示当前麻雀最好和最差适应度值。
1.3 SSA优化VMD为降低风电功率的非平稳性,采用VMD对功率信号进行分解。VMD分解前需要对各种参数进行手动设置,其中模态数K及惩罚因子α对分解结果影响较大,设置不当会严重影响分解结果,其余参数通常设置为默认值。当模态数K设置过大时会过分解,产生频率混叠;K设置过小又会欠分解,导致信息缺失。α值设置不当也会影响信号的提取结果,对信号的重构结果影响较大。鉴于K和α两参数难以确定;且人工设置随机性大,本文使用SSA对VMD的[K,α]进行寻优。
优化算法寻优前适应度函数的构造也尤为重要。排列熵值的大小可表示时间序列信号Xi的随机程度,分解产生的各IMF分量熵值越小表明序列越规律,反之表明序列越复杂,随机性越大。
设一组长度为N的时间序列为u(1),u(2),…,u(N),设置m和L值后对其重构,重构后的各子序列Xi表示如下:
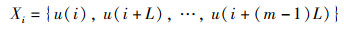
|
(8) |
式中,m表示嵌入维度,L表示延迟时间。
对每个Xi内部进行递增排序有:
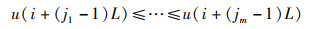
|
(9) |
其中,每一个Xi被映射到一个符号序列S(K)=(j1,j2,…,jm)中,K∈(1,m!)。将所有的符号序列表示为概率分布P1,P2,…,PK的形式,计算Shannon熵,则u(1),u(2),…,u(N)的排列熵为
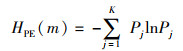
|
(10) |
为方便表示,将排列熵值进行归一化:
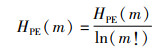
|
(11) |
Pearson相关系数可以衡量两种信号序列之间的相关程度,其值范围在[-1, 1]内,绝对值越大表明两信号的相关性越强,因此可用Pearson相关系数作为衡量原始风功率信号与重构信号偏差的一种指标,其公式如式(12):
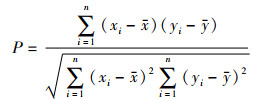
|
(12) |
式中,xi和yi分别表示原始风电功率信号和重构信号,x和y分别为对应的均值。
VMD分解的输出变量omega指示了被估计模态的中心频率,能反映各IMF分量的中心频率特征。其结果值与omega结果矩阵中VMD的收敛迭代代数直接相关,迭代数越少表明信号分解收敛越快,各分量的频率特征越明显。因此将其作为适应度函数评估指标之一。
本文综合3种VMD分解的相关指标组成综合评价指标构造适应度函数,以更准确地寻找VMD分解中稳定性及规律性最好的分量。本文构建的综合评价指标适应度函数f公式:
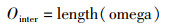
|
(13) |
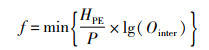
|
(14) |
式中,Ointer表示VMD的收敛迭代数,lg(Ointer)表示取迭代数的对数值。
以f作为SSA优化VMD的适应度函数,对参数[K,α]进行寻优,优化流程步骤为:
1) 初始化参数组合[K,α]及其范围,初始化麻雀种群参数,将综合适应度指标作为适应度函数。
2) 计算当前各麻雀适应度大小,找出最优最差适应度值及对应位置。
3) 一次迭代后对各麻雀适应度重新计算,并更新麻雀个体位置信息。根据麻雀当前状态,对整个麻雀种群的最优最差适应度值和位置进行更新。
4) 判断是否满足最大迭代,若满足,则输出最佳麻雀个体[K,α],否则返回2) 继续迭代。
5) 由SSA优化后的参数组合[K,α],对功率信号进行VMD分解。
优化流程图如图 1所示。
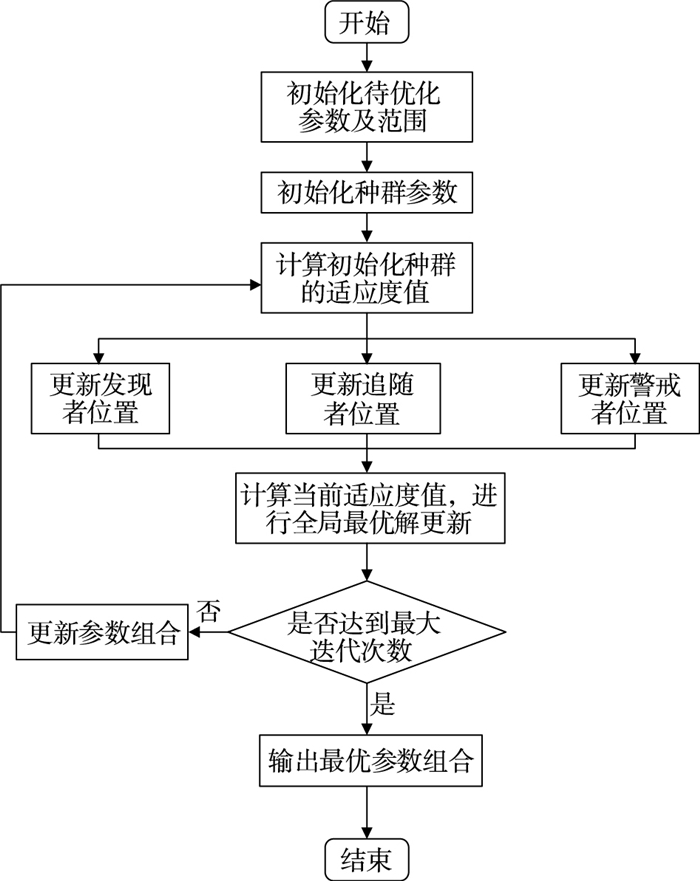
|
| 图 1 SSA优化VMD流程图 Fig.1 Flow chart of SSA optimized VMD |
核极限学习机KELM模型是在极限学习机ELM模型基础上的一种改进,通过引入核函数映射代替隐含层输入输出之间的随机映射关系,在保留ELM良好预测性能的同时,因其无需给定隐含层节点数,从而避免了人工设置节点数使训练结果随机性大的问题,具有更好的稳健性。KELM通过将低维空间中的非线性不可分数据转化为线性可分数据,有效提高了ELM的鲁棒性及泛化能力,更擅长解决回归预测问题。核极限学习机的模型结构图如图 2所示。
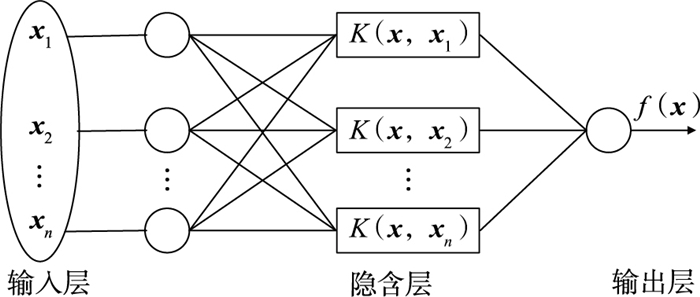
|
| 图 2 核极限学习机模型结构图 Fig.2 The structure of the kernel extreme learning machine model |
对于给定的输入样本,KELM的预测输出为
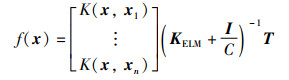
|
(15) |
式中,C是正则化系数,I和T分别是对角矩阵和目标向量矩阵,K(x,xi)是核函数,KELM是核矩阵。
核矩阵KELM定义如下:
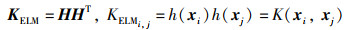
|
(16) |
式中,HHT表示ELM中的随机矩阵,在KELM中将由核矩阵KELM代替。
核函数选择不同,模型的预测性能也存在较大差异,采用单一核函数的KELM通常也难以适应风电功率这样的多特征样本。核函数包含多种类型,其中径向基函数(radial basis function,RBF)为典型的局部型核函数,学习能力强泛化能力弱;多项式(polynomial,Poly)核为典型的全局型核函数,学习能力较弱泛化能力强。为进一步提升核极限学习机的学习和泛化性能,本文结合RBF和Poly核函数的优点,组成混合核函数构造混合核极限学习机HKELM预测模型[26-27],从而更好地学习风电功率与特征因素之间的非线性关系。混合核函数的计算公式如式(17)~式(19):
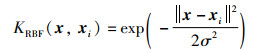
|
(17) |
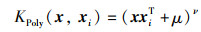
|
(18) |
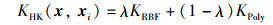
|
(19) |
式中,σ为RBF核的核参数;μ和ν为Poly核的核参数;λ为两核间的权重系数,λ∈(0,1)。
从混合核函数的计算公式及核极限学习机输出形式可知,HKELM模型中参数较多,参数设置对模型的精度也影响较大。为避免人工选择参数效率低,且回归精度难以最优的缺点,利用SSA对HKELM模型的正则化系数、混合核函数的核参数以及权重进行寻优,即优化目标G =[C,σ,μ,ν,λ],其优化流程步骤与SSA优化VMD类似,这里本文不再赘述。
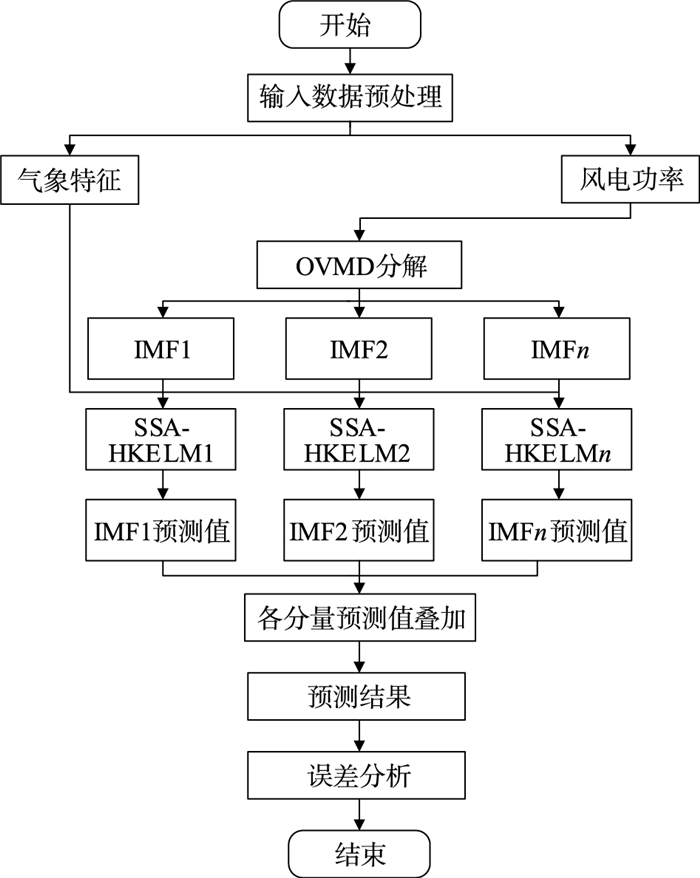
2 基于OVMD-SSA-HKELM的短期风电功率预测风电功率具有较强的波动性及非平稳性,因此为提升可预测性,本文设计一个综合评价指标作为SSA优化VMD的适应度函数,将风电功率分解为一组相对平稳的IMF分量。对各分量划分训练集和测试集,在训练集上训练各分量的HKELM预测模型,并使用SSA对模型参数进行优化。在测试集上将气象特征因素输入预测模型进行预测,得到各IMF分量预测值,叠加各分量的预测值,得到最终预测值,并验证所建模型性能。本文构建了基于OVMD-SSA-HKELM的短期风电功率预测模型,模型流程图如图 3所示。
|
| 图 3 OVMD-SSA-HKELM模型流程图 Fig.3 Flow chart of OVMD-SSA-HKELM model |
具体流程步骤:
1) 对输入数据进行预处理并划分数据集,利用SSA优化后的VMD将原始功率数据分解为一组平稳IMF分量。
2) 在训练集上训练各IMF分量的HKELM预测模型,并使用SSA对模型参数寻优。
3) 将各分量测试集输入量输入已训练好的SSA-HKELM模型,得到各IMF分量预测值。
4) 叠加各分量预测值,得到最终预测结果值。
5) 对预测结果进行误差分析,分析模型性能。
2.1 数据预处理及初始化1) 将原始风电功率数据代入SSA优化后的VMD模型分解,将分解后各分量与气象特征的风速、风向数据组成若干输入数据向量。
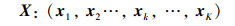
|
(20) |
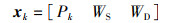
|
(21) |
式中,1<k<K,Pk表示分解后的第k个风电功率分量;WS表示风速;WD表示风向。
2) 由于本文为多变量进行预测,不同变量之间的量纲各有不同,为减轻量纲对模型训练及预测结果的影响,对数据根据式(22)进行标准化处理。标准化公式为
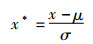
|
(22) |
式中,x*表示标准化后的数据,x表示实际值,μ和σ分别表示每一列样本数据的均值和方差。为方便后续误差评价指标的计算与分析,对预测结果反归一化,使功率数据返回原来的量级。
2.2 评价指标为验证本文所提方法性能,使用均方根误差(root mean square error,RMSE)、平均绝对误差(mean absolute error,MAE)、平均绝对百分比误差(mean absolute percentage error,MAPE)三个误差指标对模型预测效果进行评估,其公式如下:
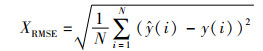
|
(23) |
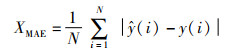
|
(24) |
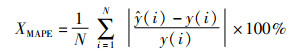
|
(25) |
式中,N代表样本个数;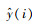
为验证本文所提方法的有效性,采用中国内蒙古某风电场2020年1月份实际发电功率数据与气象数据作为实验数据,数据采样间隔15 min。选取1月1日—1月30日共2 880个数据样本作为训练集,1月31日的96个数据样本作为测试集。
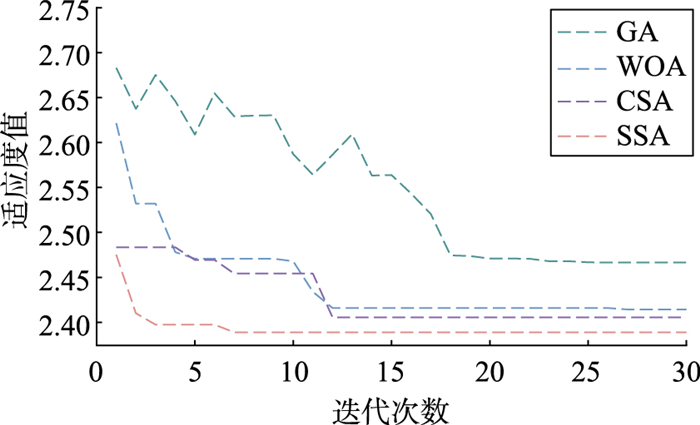
3.1 VMD分解结果及SSA优化性能分析风电功率序列具有波动性及非平稳性,为提升预测精度,采用VMD将原始功率序列分解。考虑VMD分解时模态数K及惩罚因子α难以人为确定,而SSA算法相比其他传统的智能优化算法有着较好的寻优精度和收敛速度,且稳定性更好[28-29],因此采用SSA对参数[K,α]寻优。同时为验证SSA优化性能,将SSA分别与遗传算法(genetic algorithm,GA)、布谷鸟搜索算法(cuckoo search algorithm,CSA)、鲸鱼优化算法(whale optimization algorithm,WOA)进行对比。实验中设置各优化算法的种群数量均为20,迭代次数为30,寻优范围K∈[3, 12],α∈[100,2 500],适应度迭代曲线及寻优结果如图 4和表 1所示。
|
| 图 4 适应度迭代曲线 Fig.4 Fitness iteration curve |
| 模型 | 分解参数 | 分解适应度 | |
| 模态数 | 惩罚因子 | ||
| GA-VMD | 7 | 1 698 | 2.466 |
| WOA-VMD | 6 | 2 396 | 2.414 |
| CSA-VMD | 6 | 2 159 | 2.405 |
| SSA-VMD | 5 | 1 683 | 2.389 |
从图 4可以看出,GA在迭代时适应度极不稳定,且算法收敛较慢,寻优能力最差;WOA相较于GA寻优精度得到了较大提升,但算法在迭代后期并未完全收敛,收敛速度最慢;CSA虽然相对收敛较快,但与SSA相比适应度值仍较高;SSA在第8次迭代时就已完成收敛,具有更快的收敛速度,且适应度值更低,寻优能力更强。相比于另外3种优化算法,SSA的这些优势主要得益于麻雀种群间分工明确,相互之间协同性强,以及侦查预警机制在种群中的警戒监察作用,且在迭代过程中能将种群中的所有因素考虑在内,使种群中的麻雀向全局最优值移动,迅速在最优值附近收敛。因此,在4种算法中SSA寻优能力最佳。从表 1也可以发现,SSA-VMD取得了最优的综合指标值,算法寻优精度最高,因此采用SSA寻优后的参数进行风电功率分解,分解结果图如图 5所示。

|
| 图 5 VMD分解结果 Fig.5 Decomposition results of VMD |
为验证本文所提方法的有效性,与相关单一及组合模型进行对比,对比实验基准模型信息描述如表 2所示。
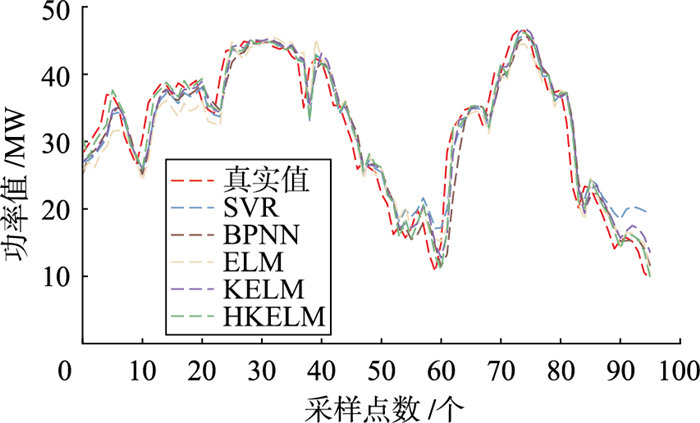
表 2中SVR采用径向基(RBF)核函数,gamma取0.01;BPNN神经元个数取64,激活函数为tanh;ELM采用双隐含层,神经元个数分别64和30,激活函数为tanh;KELM采用RBF核函数,正则化系数C=10,核参数σ=1;HKELM为RBF和Poly混合核函数,权重系数λ=0.5,正则化系数C= 10,混合核参数σ、μ、ν均为1。组合方法OVMD-KELM和OVMD-HKELM中的KELM和HKELM模型采用与单一KELM和HKELM模型相同的初始化参数设置,除此之外,各组合方法中VMD和HKELM的参数均由优化算法寻优所得。各单一模型预测结果如图 6所示,误差指标如表 3所示。
|
| 图 6 各单一模型预测结果 Fig.6 Prediction results of each single model |
| 预测模型 | RMSE /MW | MAE /MW | MAPE /% |
| SVR | 3.469 9 | 2.615 4 | 8.007 4 |
| BPNN | 3.462 2 | 2.492 6 | 7.859 4 |
| ELM | 3.396 9 | 2.584 0 | 8.205 3 |
| KELM | 3.038 5 | 2.240 1 | 6.952 9 |
| HKELM | 2.739 8 | 1.928 4 | 5.995 8 |
从图 6可看出,各单一模型虽能预测出真实值的变化趋势,但在波动剧烈及尖峰的样本点处仍有不小的拟合误差,其中HKELM模型预测偏差相对较小,具有更好的预测精度。从表 3也可以发现HKELM模型相比于KELM三种误差指标分别提升了9.83%,13.91%和13.77%。表明相比于采用单一核函数的KELM模型,采用混合核函数的HKELM模型具有更好的学习能力,更适合处理风电功率这种波动性较强的数据。
本文方法与各组合方法的预测结果如图 7所示,误差指标如表 4所示。

|
| 图 7 各组合模型预测结果 Fig.7 Prediction results of each combination model |
| 预测模型 | RMSE /MW | MAE /MW | MAPE /% |
| OVMD-KELM | 1.256 3 | 1.043 6 | 3.225 5 |
| OVMD-HKELM | 0.778 4 | 0.624 8 | 1.944 7 |
| EEMD-SSA-HKELM | 1.015 5 | 0.737 4 | 2.292 0 |
| CVMD-SSA-HKELM | 0.726 6 | 0.569 4 | 1.782 6 |
| OVMD-SSA-HKELM | 0.490 8 | 0.392 2 | 1.219 9 |
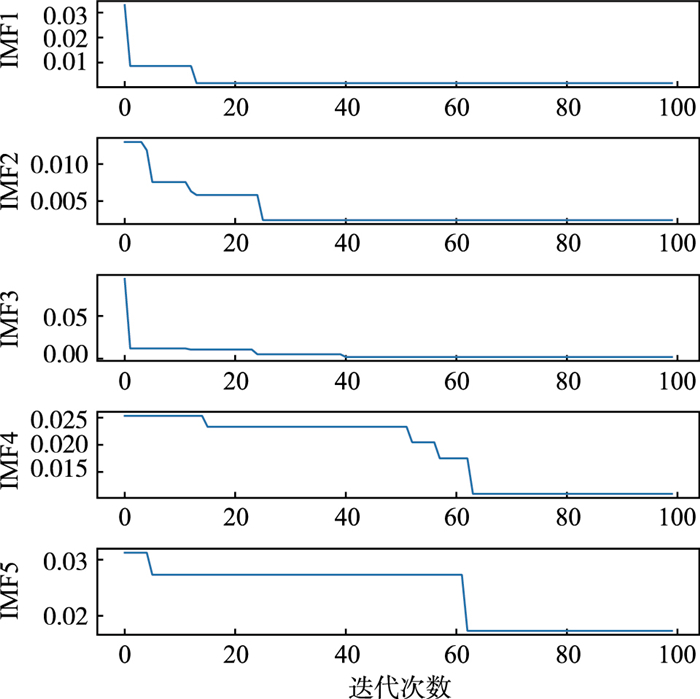
结合图 6图 7可以看出,相比于单一模型,加入分解策略后的各组合方法的预测结果更贴近真实值,其中本文所提方法的拟合效果更好,在尖峰及功率波动处具有更小的预测误差。从表 4也可以发现,对功率分解后再进行预测,采用混合核函数的HKELM模型相比于KELM三种误差指标也分别提升了38.04%,40.13%和39.71%。进一步表明了混合核极限学习机模型具有更好的学习及泛化能力,预测精度更高。为进一步提高预测精度,本文方法使用SSA对各分量HKELM的相关超参数进行寻优,相比于未寻优的OVMD-HKELM模型三种误差指标分别提升了36.95%,33.48%和37.27%。表明通过优化算法对相关超参数寻优,有效克服了手动设置参数随机性大且难以发挥模型性能的局限性。SSA优化的适应度变化图如图 8所示。从图 8可以看出,各分量优化时的收敛速度逐渐减低,分量1在迭代15次时已完成收敛,分量4和分量5均在迭代60次后才开始收敛,这主要由于相比于分量4分量5这样的高频分量,分量1的规律性更好,波动性更小,更有利于预测。
|
| 图 8 各分量的适应度变化图 Fig.8 The fitness change diagram of each component |
从表 4还可以发现,相比于采用EEMD分解的EEMD-SSA-HKELM模型,本文方法的3种误差指标分别提升了51.67%、46.81%和46.78%。表明VMD可有效克服EEMD残留噪声的影响,使模型更易学习各分量与特征间的联系。相比于CVMD-SSA- HKELM模型,本文方法的3种误差指标分别提升了32.45%、31.12%和31.57%。表明SSA优化VMD分解后的各分量更具稳定性和规律性,与原始序列的差别更小,可预测性更好。综合来看,本文所提方法具有更高的预测精度,模型的适应性更好。
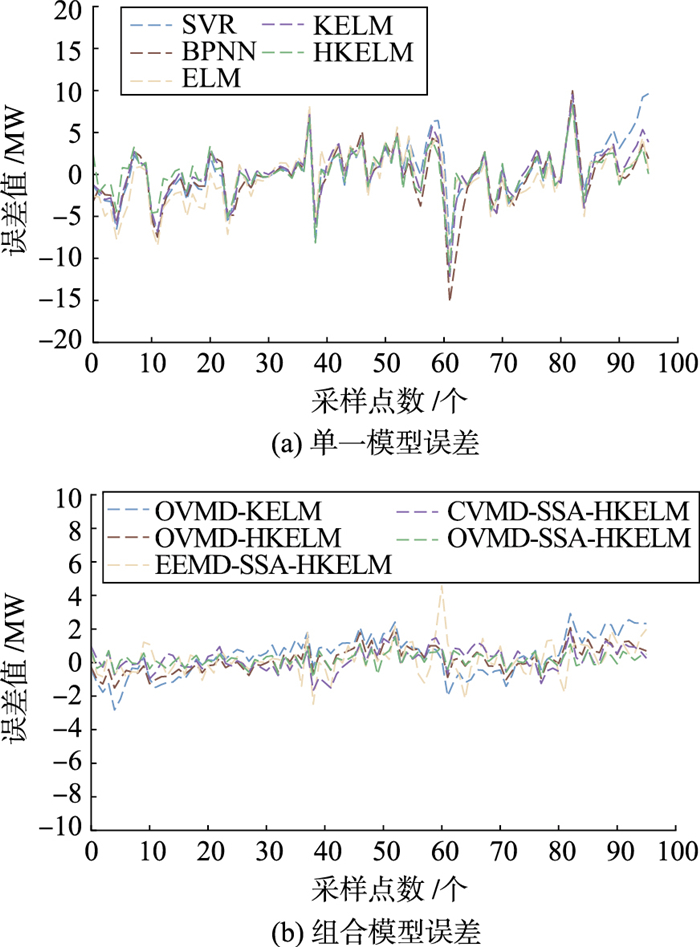
图 9为各单一及组合模型的误差对比图。从图 9可以直观看出,单一模型的误差值波动更大,误差最大达到15 MW左右,具有较大的误差,表明单一模型并不能满足风电功率这种波动性较强数据的预测精度需求。各组合模型相比于单一模型的误差波动及误差值更小,预测性能有了较大提升,其中本文所提方法的预测误差更接近于0值,进一步表明本文方法的预测精度更好。
|
| 图 9 单一及组合模型误差值对比 Fig.9 Comparison of error values of single and combined model |
为进一步验证本文所提方法的准确性与泛化性,选取内蒙古某风电场8月份以及与内蒙古风电场经纬度不同的宁夏某风电场1月份实际数据进行验证。与之前实验中所用内蒙古1月份数据相比,两数据分别由于季节差异和地理位置的不同,相关气象特征尤其是风速情况各有差异,其中宁夏1月份数据也由于场站风机信息的差异,具有更高的额定出力功率。两数据的采样时间间隔均为15 min,均选取前30天2 880个样本点用于训练,最后一天96个样本点进行测试。各模型8月及1月预测结果如图 10和图 11所示,误差指标如表 5所示。
|
| 图 10 各模型8月预测结果 Fig.10 Prediction results of each model in August |

|
| 图 11 各模型1月预测结果 Fig.11 Prediction results of each model in January |
| 月份 | 预测模型 | RMSE /MW | MAE /MW | MAPE /% |
| 8月 | OVMD-KELM | 0.937 6 | 0.651 7 | 4.037 2 |
| OVMD-HKELM | 0.630 6 | 0.492 3 | 2.670 5 | |
| EEMD-SSA-HKELM | 0.809 6 | 0.581 7 | 3.174 0 | |
| OVMD-SSA-HKELM | 0.404 7 | 0.313 0 | 1.705 2 | |
| 1月 | OVMD-KELM | 1.729 5 | 1.388 3 | 2.665 2 |
| OVMD-HKELM | 1.337 8 | 1.089 6 | 2.110 9 | |
| EEMD-SSA-HKELM | 1.936 7 | 1.548 6 | 2.997 8 | |
| OVMD-SSA-HKELM | 0.919 6 | 0.771 0 | 1.494 2 |
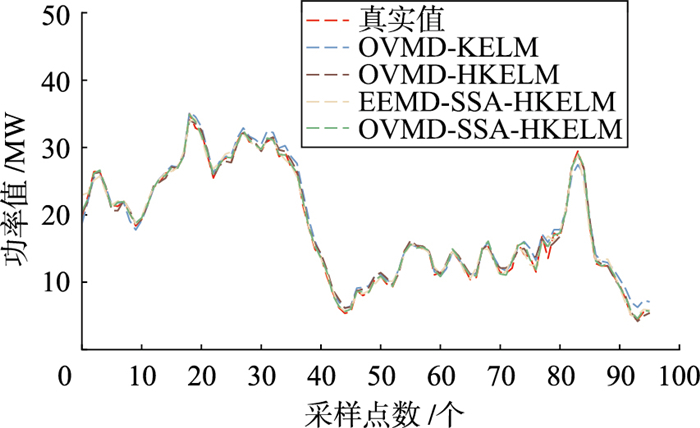
从图 10可以看出,在最后的几个样本点处,OVMD-KELM模型预测值与真实值之间出现了较大偏差,而本文方法的预测值相比其他方法则更贴近真实值,且在功率急速升降的样本点处本文方法仍具有更好的拟合效果。从图 11也可以看出,相比于内蒙古8月份数据,所选宁夏1月份数据测试样本点的波动性更大,在功率波动较快的10~26样本点及80~96样本点处,本文方法预测值相比其他方法与真实值的吻合度更高,整体的拟合效果也更好。综合两图可以看出,本文方法在8月和1月两数据中预测结果的拟合效果相比于其他方法均最好,模型具有较好的适应性。从表 5也可以发现在8月和1月数据中,本文方法的MAPE值分别达到1.705 2%和1.494 2%,均保持在2%以内,且在几种模型中均具有最高的精度,进一步证明了本文方法具有较好的准确性与泛化性。
4 结论针对风电功率的波动性及非平稳性,本文提出一种基于SSA优化VMD-HKELM的短期风电功率预测方法,通过仿真实验对比得出如下结论:
1) 综合排列熵、Pearson相关系数及VMD迭代代数三种指标设计一种SSA优化VMD的适应度函数,在提高VMD分解自适应性的同时,实现了对分解量平稳性及规律性更为精准有效的判别,克服了VMD参数难调、手动设置参数随机性大的问题,为最大化提高风电功率预测精度奠定了基础。
2) 结合全局性Poly核与局部性RBF核函数的优点,构建HKELM预测模型,有效提高了预测模型的学习与泛化能力。引入收敛速度与寻优能力较强的SSA对HKELM模型的参数进行优化,解决了HKELM模型参数多、人工选取难度大的问题,大大提高了预测精度。
3) 通过与多种单一及组合方法对比,仿真实验表明,本文所提方法的预测精度更高且泛化性能更好。值得注意的是,在设定好SSA算法基础参数后,本文方法无需再手动调节参数,有效避免了手动调参的繁琐性及随机性,具有较强的自适应性及智能性。
风电功率出力受影响因素较多,因此后续研究将考虑加入更多特征影响因素,同时开展四季等更大范围的预测。
| [1] |
袁铁江, 曹继雷. 计及风电-负荷不确定性的风氢低碳能源系统容量优化配置[J]. 高电压技术, 2022, 48(6): 2037-2044. YUAN T J, CAO J L. Capacity optimization allocation of wind hydrogen low-carbon energy system considering wind power-load uncertainty[J]. High Voltage Engineering, 2022, 48(6): 2037-2044. DOI:10.13336/j.1003-6520.hve.20210340 |
| [2] |
LIU H, CHEN C, LYU X W, et al. Deterministic wind energy forecasting: A review of intelligent predictors and auxiliary methods[J]. Energy Conversion and Management, 2019, 195(1): 328-345. |
| [3] |
唐新姿, 顾能伟, 黄轩晴, 等. 风电功率短期预测技术研究进展[J]. 机械工程学报, 2022, 58(12): 213-236. TANG X Z, GU N W, HUANG X Q, et al. Progress on short term wind power forecasting technology[J]. Journal of Mechanical Engineering, 2022, 58(12): 213-236. |
| [4] |
宋家康, 彭勇刚, 蔡宏达, 等. 考虑多位置NWP和非典型特征的短期风电功率预测研究[J]. 电网技术, 2018, 42(10): 3234-3242. SONG J K, PENG Y G, CAI H D, et al. Research of short-term wind power forecasting considering multi-location NWP and uncanonical feature[J]. Power System Technology, 2018, 42(10): 3234-3242. DOI:10.13335/j.1000-3673.pst.2018.0492 |
| [5] |
余沣, 董存, 王铮, 等. 考虑山东近海不同风能天气特征的风电功率区间预测模型[J]. 电网技术, 2020, 44(4): 1238-1247. YU F, DONG C, WANG Z, et al. Wind power interval forecasting model considering different wind energy weather characteristics in Shandong offshore areas[J]. Power System Technology, 2020, 44(4): 1238-1247. DOI:10.13335/j.1000-3673.pst.2019.1058 |
| [6] |
杨茂, 周宜. 计及风电场状态的风电功率超短期预测[J]. 中国电机工程学报, 2019, 39(5): 1259-1268. YANG M, ZHOU Y. Ultra-short-term prediction of wind power considering wind farm status[J]. Proceedings of the CSEE, 2019, 39(5): 1259-1268. DOI:10.13334/J.0258-8013.PCSEE.180873 |
| [7] |
LU P, YE L, PEI M, et al. Coordinated control strategy for active power of wind power cluster based on model[J]. Proceedings of the CSEE, 2021, 41(17): 5887-5899. |
| [8] |
KORPRASERTSAK N, LEEPHAKPREEDA T. Robust short-term prediction of wind power generation under uncertainty via statistical interpretation of multiple forecasting models[J]. Energy, 2019, 180: 387-397. DOI:10.1016/j.energy.2019.05.101 |
| [9] |
赵倩, 黄景涛. 基于EMD-SA-SVR的超短期风电功率预测研究[J]. 电力系统保护与控制, 2020, 48(4): 89-96. ZHAO Q, HUANG J T. On ultra-short-term wind power prediction based on EMD-SA-SVR[J]. Power System Protection and Control, 2020, 48(4): 89-96. |
| [10] |
刘兴, 王艳, 纪志成. 基于随机森林的风电功率短期预测方法[J]. 系统仿真学报, 2021, 33(11): 2606-2614. LIU X, WANG Y, JI Z C. Short-term wind power prediction method based on random forest[J]. Journal of System Simulation, 2021, 33(11): 2606-2614. |
| [11] |
张群, 唐振浩, 王恭, 等. 基于长短时记忆网络的超短期风功率预测模型[J]. 太阳能学报, 2021, 42(10): 275-281. ZHANG Q, TANG Z H, WANG G, et al. Ultra-short-term wind power prediction model based on long and short term memory network[J]. Acta Energiae Solaris Sinica, 2021, 42(10): 275-281. |
| [12] |
SHAHID F, ZAMEER A, MUNEEB M. A novel genetic LSTM model for wind power forecast[J/OL]. Energy, 2021, 223[2022-01-06] https://www.sciencedirect.com/science/article/pii/s0360544221003182. DOI: 10.1016/j.energy.2021.120069.
|
| [13] |
王雨城, 曾宪文, 高桂革. 基于GRU网络的风功率短期预测模型[J]. 仪表技术, 2020(1): 9-12, 39. WANG Y C, ZENG X W, GAO G G. Short-term forecast model of wind power based on GRU network[J]. Instrument Technology, 2020(1): 9-12, 39. |
| [14] |
NIU Z W, YU Z Y, TANG W H, et al. Wind power forecasting using attention-based gated recurrent unit network[J/OL]. Energy, 2020, 196[2022-02-08] https://www.sciencedirect.com/science/article/pii/s03605442203031882. DOI: 10.1016/j.energy.2020.117081.
|
| [15] |
李国庆, 刘钊, 金国彬, 等. 基于随机分布式嵌入框架及BP神经网络的超短期电力负荷预测[J]. 电网技术, 2020, 44(2): 437-445. LI G Q, LIU Z, JIN G B, et al. Ultra-short-term power load forecasting based on randomly distributive embedded framework and BP neural network[J]. Power System Technology, 2020, 44(2): 437-445. |
| [16] |
刘栋, 魏霞, 王维庆, 等. 基于SSA-ELM的短期风电功率预测[J]. 智慧电力, 2021, 49(6): 53-59, 123. LIU D, WEI X, WANG W Q, et al. Short-term wind power prediction based on SSA-ELM[J]. Smart Power, 2021, 49(6): 53-59, 123. |
| [17] |
杨锡运, 康宁, 杨雨薇, 等. 基于EEMD的SOA-KELM风电功率概率性短期区间预测[J]. 动力工程学报, 2019, 39(11): 926-933, 952. YANG X Y, KANG N, YANG Y W, et al. Probabilistic short-term interval forecast of wind power based on EEMD and SOA-KELM model[J]. Chinese Journal of Power Engineering, 2019, 39(11): 926-933, 952. |
| [18] |
NAIK J, SATAPATHY P, DASH P K. Short-term wind speed and wind power prediction using hybrid empirical mode decomposition and kernel ridge regression[J]. Applied Soft Computing, 2018, 70: 1167-1188. |
| [19] |
李军, 李大超. 基于CEEMDAN-FE-KELM方法的短期风电功率预测[J]. 信息与控制, 2016, 45(2): 135-141. LI J, LI D C. Short-term wind power forecasting based on CEEMDAN-FE-KELM method[J]. Information and Control, 2016, 45(2): 135-141. |
| [20] |
王瑞, 陈泽坤, 逯静. 基于VMD和IBA-LSSVM的短期风电功率预测[J]. 河海大学学报(自然科学版), 2021, 49(6): 575-582. WANG R, CHEN Z K, LU J. Short-term prediction of wind power based on VMD and IBA-LSSVM[J]. Journal of Hohai University (Natural Science), 2021, 49(6): 575-582. |
| [21] |
曾亮, 雷舒敏, 王珊珊, 等. 基于OVMD-SSA-DELM-GM模型的超短期风电功率预测方法[J]. 电网技术, 2021, 45(12): 4701-4712. ZENG L, LEI S M, WANG S S, et al. Ultra-short-term wind power prediction based on OVMD-SSA-DELM-GM model[J]. Power System Technology, 2021, 45(12): 4701-4712. |
| [22] |
鹿凯, 石开明, 贾欢, 等. 基于自适应变分模态分解的组合模型风电功率预测[J/OL]. 电源学报. (2021-11-23)[2022-05-14]. https://kns.cnki.net/kcms/detail/12.1420.TM.20211122.1634.006.html. LU K, SHI K M, JIA H, et al. wind power prediction of combined model based on variational modal decomposition[J/OL]. Journal of Power Supply. (2021-11-23)[2022-05-14]. https://kns.cnki.net/kcms/detail/12.1420.TM.20211122.1634.006.html. |
| [23] |
李青, 张新燕, 马天娇, 等. 基于ECBO-VMD-WKELM的风电功率超短期多步预测[J]. 电网技术, 2021, 45(8): 3070-3080. LI Q, ZHANG X Y, MA T J, et al. Multi-step ahead ultra-short term forecasting of wind power based on ECBO-VMD-WKELM[J]. Power System Technology, 2021, 45(8): 3070-3080. |
| [24] |
林涛, 蔡睿琪, 张丽, 等. 基于IBA-KELM的风电功率区间预测方法[J]. 可再生能源, 2018, 36(7): 1092-1097. LIN T, CAI R Q, ZHANG L, et al. Prediction intervals forecasts of wind power based on IBA-KELM[J]. Renewable Energy Resources, 2018, 36(7): 1092-1097. |
| [25] |
XUE J, SHEN B. A novel swarm intelligence optimization approach: Sparrow search algorithm[J]. Systems Science & Control Engineering An Open Access Journal, 2020, 8(1): 22-34. |
| [26] |
李可军, 徐延顺, 魏本刚, 等. 基于PSO-HKELM的变压器顶层油温预测模型[J]. 高电压技术, 2018, 44(8): 2501-2508. LI K J, XU Y S, WEI B G, et al. Prediction model for top oil temperature of transformer based on hybrid kernel extreme learning machine trained and optimized by particle swarm optimization[J]. High Voltage Engineering, 2018, 44(8): 2501-2508. |
| [27] |
郭建帅, 崔双喜, 郭建斌, 等. 基于VMD-SSA-HKELM的超短期负荷预测[J]. 国外电子测量技术, 2022, 41(6): 105-111. GUO J S, CUI S X, GUO J B, et al. Ultra-short-term load prediction based on VMD-SSA-HKELM[J]. Foreign Electronic Measurement Technology, 2022, 41(6): 105-111. |
| [28] |
李雅丽, 王淑琴, 陈倩茹, 等. 若干新型群智能优化算法的对比研究[J]. 计算机工程与应用, 2020, 56(22): 1-12. LI Y L, WANG S Q, CHEN Q R, et al. Comparative study of several new swarm intelligence optimization algorithms[J]. Computer Engineering and Applications, 2020, 56(22): 1-12. |
| [29] |
张九龙, 王晓峰, 芦磊, 等. 若干新型智能优化算法对比分析研究[J]. 计算机科学与探索, 2022, 16(1): 88-105. ZHANG J L, WANG X F, LU L, et al. Analysis and research of several new intelligent optimization algorithms[J]. Computer Science and Exploration, 2022, 16(1): 88-105. |



