2. 韶关学院信息工程学院, 广东 韶关 512026;
3. 中南大学计算机学院, 湖南 长沙 410083
2. College of Information Engineering, Shaoguan University, Shaoguan 512026, China;
3. College of Computer Science and Engineering, Central South University, Changsha 410083, China
0 引言
DCNN(deep convolutional neural network)[1]是一类包含卷积计算且含有深层次结构的前馈神经网络,具有良好的特征提取能力和泛化能力,被广泛应用于图像分类[2]、目标跟踪与检测[3-4]、自然语言处理[5]、场景分类[6]、人脸识别[7]等各个领域。然而随着大数据时代[8]的到来,各个领域所产生的数据呈爆发式增长,传统DCNN模型的训练代价会随数据量的增长呈指数型增加,模型训练的复杂度也因大数据环境下任务复杂性的增长呈上升趋势。因此,设计适用于大数据环境下的DCNN算法具有十分重要的意义。
近年来,MapReduce分布式计算模型因其在处理大数据方面具有容错性高和可扩展性强等优点,深受广大学者的青睐。目前已有大量基于MapReduce框架的并行DCNN算法成功运用到了大数据的分析和处理领域当中。例如BASIT等[9]结合MapReduce提出了DC-CNN(distributed computing CNN)训练算法,该算法采用并行计算的方式对各分布式节点上的模型进行训练,实现了CNN模型在分布式计算系统上的并行化训练过程,相较于单机器的训练方式,拥有更高的训练效率。基于此,LEUNG等[10]在批训练过程中设计了参数的并行更新策略,提出了MR-PCNN(Parallel CNN based on MapReduce)算法,该算法通过并行化多个批训练过程实现了模型参数的并行更新,提升了模型参数的更新效率,进而提升了模型的训练效率。为进一步提升模型的训练效率,WANG等[11]在参数更新阶段运用了并行化矩阵乘法运算替换传统卷积运算的思想,提出了MR-MPC(Matrix Parallel Computing method based on MapReduce)算法,该算法通过并行化矩阵乘法的方式提升卷积的运算性能,提高参数更新的迭代速度,从而提升模型的训练效率。LI等[12]则在参数组合阶段引入了集中式参数服务器的思想,提出了MR-CNN(MapReduce-based CNN)训练算法,该算法通过使用HDFS(hadoop distributed file system)作为参数服务器实现了各节点之间模型参数更新的共享,提升了模型参数的并行化合并效率,进而提升了模型总体的训练效率。此外,HU等[13]提出了基于Im2col的并行深度卷积神经网络优化算法(IA-PDCNNOA),该算法在批训练过程中通过使用先滤波后筛选的策略实现了输入特征的有效筛选,降低了参数并行更新的迭代次数,进而提升了模型总体的训练性能。虽然以上5种并行DCNN算法对模型训练的效率均有所提升,但是仍存在以下不足:1) 在批训练过程中,无论采用的是并行方式还是非并行方式,其训练过程均会产生大量的冗余特征,若不对这些冗余特征进行必要的筛选,将会给模型训练带来冗余特征计算过多的问题。2) 在参数更新阶段,虽然采用并行化矩阵乘法的方式可以在一定程度上加速卷积结果的生成,但是该并行化的操作并未改变卷积的计算量,且计算过程需要频繁的输入/输出(IO)操作,在计算密集的训练过程中仍会出现卷积运算性能不足的问题。3) 在参数组合阶段,由于模型参数的组合速率会因各分布式节点计算能力的偏差而受到影响,因此极易引起各节点之间出现互相等待的现象,延长分布式系统中各节点的平均反应时长,致使模型在组合阶段产生参数并行化合并效率低的问题。
针对以上问题,提出了基于Winograd卷积的并行深度卷积神经网络(Winograd-based parallel deep convolutional neural network,WP-DCNN)优化算法,算法的主要工作有:
1) 设计了FF-CSNMI(feature filtering based on cosine similarity and normalized mutual information)策略。该策略从输入特征图入手,通过先从输入特征图中筛选出表征特征图,再将其与冗余特征图融合构建出新的输入特征图,以此消除通道间对于冗余特征图的计算,从而解决了冗余特征计算过多的问题。
2) 结合MapReduce提出了MR-PWC(MapReduce-based parallel winograd convolution)策略。该策略通过使用并行化Winograd卷积替换传统卷积运算的方式来提升卷积运算的性能,此外为满足并行化的需要,提出了等大小切分函数FESS(X) 与等间距切分函数FEDS(X),进一步优化了并行Winograd卷积的运算性能,从而解决了大数据环境下卷积运算性能不足的问题。
3) 提出了LB-TM(load balancing based on task migration)策略。该策略通过使用动态阈值加任务迁移的方式来均衡各节点之间的负载,以此降低并行系统中各节点的平均反应时长,提升了模型参数并行化合并时的效率,从而解决了参数并行化合并效率低的问题。
1 相关概念介绍 1.1 归一化互信息定义1(归一化互信息) 归一化互信息[14]是度量两张图片之间相似性的一种表达方式,该值越大代表两张图片的相似性越高,反之越低。假设有图像F和图像G,则其归一化互信息INMI(F,G)的定义为
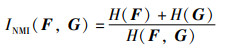
|
(1) |
其中,H(F)和H(G)分别为图像F和图像G的信息熵,H(F,G)为两者的联合熵。
1.2 余弦相似度定义2(余弦相似度) 余弦相似度[15-16]又称余弦相似性,是通过计算两个向量内积空间的余弦值来度量它们之间的相似性,该值越大代表两者的相似性越高,反之越低。假设有图像X和图像Y,则其余弦相似度CSIM(X,Y)的定义为
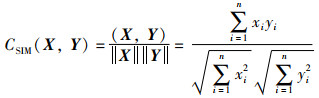
|
(2) |
定义3(Winograd卷积算法) Winograd卷积算法[17-18]源自Winograd提出的最小滤波算法,通过对输入特征图和权重上的一系列变换来减少乘法运算次数。在2维数据情况下,若输出特征图Y和过滤器W的尺寸分别为m×m和r×r,则该最小滤波算法可记为F(m×m,r×r),其矩阵形式为
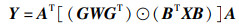
|
(3) |
其中,⊙表示逐元素乘,X为尺寸(m+r-1)×(m+r-1)的输入特征图,AT、G和BT分别表示与F(m×m,r×r)算法匹配的转换系数矩阵,其值由m和r来决定。
2 WP-DCNN算法WP-DCNN算法主要包含3个阶段:冗余特征筛选、参数并行更新、参数并行合并。各阶段的主要任务是:1) 冗余特征筛选阶段:设计了FF-CSNMI策略,先筛选出输入特征图中的冗余特征再将其融入表征特征中,以此来解决批训练过程中冗余特征计算过多的问题。2) 参数并行更新阶段:结合MapReduce框架提出MR-PWC策略,通过并行Winograd卷积运算替换传统卷积运算的方式加速卷积结果的生成,以此来提升卷积运算的性能。3) 参数并行合并阶段:提出LB-TM策略,根据各分布式节点之间的计算性能均衡各计算节点上的任务负载,以此来降低集群总体的平均反应时长,提升参数的并行化合并效率。
2.1 冗余特征筛选针对批训练过程中冗余特征计算过多的问题,提出了FF-CSNMI策略,该策略主要包含3个步骤,即特征划分、特征过滤与特征融合。
2.1.1 特征划分在特征筛选之前,需要先对输入特征图进行粗略的划分以获得初步的冗余特征集与表征特征集,具体过程为:先按比例α将卷积层中的输入特征图随机划分为采样特征集S与候选特征集C;接着提出基于余弦相似度的特征相似度度量系数CFSM来划分冗余特征集,计算C中各特征图的特征相似度度量系数CFSM,并根据其大小对特征图进行升序排序;最后按比例α从低到高将C中的特征图划分为冗余特征集R与表征特征集P两个部分。
定理1(特征相似度度量系数CFSM) 已知特征图X与均值特征矩阵E,特征图X相对于均值特征矩阵E的特征相似度度量系数CFSM为
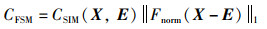
|
(4) |
其中,
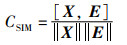
|
(5) |
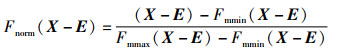
|
(6) |
式中,Fnorm(·)表示最大最小标准化函数,Fmmin(·) 和Fmmax(·)分别表示矩阵最小值函数与矩阵最大值函数。
证明 已知余弦相似度CSIM(X,E)的大小代表特征图X与均值特征矩阵E之间的相似程度,即CSIM(X,E)越大则表示X与E的相似度越大,反之则越小。Fnorm(X-E)代表了特征图X与均值特征矩阵E之间差值的归一化矩阵,该归一化矩阵表示X与E之间的相对距离,其1阶范数的大小可以反映X与E之间的偏移程度,即Fnorm(X-E)1的值越小表示偏移程度越小,反之则越大。若X与E之间的余弦相似度较小且偏移程度较高,则表示当前特征图X的特征信息难以用均值特征矩阵E的特征信息去替代,此时,X与E之间相似程度较低,同时CFSM的值较小;若X与E之间的余弦相似度较大且偏移程度较低时,则表示当前特征图X与均值特征矩阵E之间相似程度较高,此时CSIM(X,E)的值较大;因此可以使用余弦相似度CSIM(X,E)与归一化矩阵Fnorm(X-E)的1阶范数的乘积来反映特征图X与均值特征矩阵E之间的相似程度。证毕。
2.1.2 特征过滤由于在特征划分阶段仅使用比例α对候选特征集进行粗略的划分,导致表征特征集P中仍残留大量无效的冗余特征,因此仍需进一步过滤表征特征集中的冗余特征,具体过程为:首先提出基于归一化互信息的特征关联系数CFAC来过滤冗余特征,计算当前表征特征集P中各特征图的特征关联系数CFAC;接着依据CFAC的大小对特征图进行降序排序,按比例β从高到低将当前表征特征集划分为冗余特征集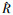
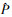
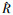
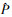
定理2(特征关联系数CFAC) 已知有特征图X与均值特征图E,特征图X的特征相似度度量系数为CFAC,则特征图X相对于均值特征矩阵E的特征关联系数CFAC为
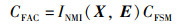
|
(7) |
其中,
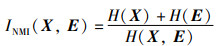
|
(8) |
证明 已知INMI(X,E)代表了特征图X与均值特征图E之间的归一化互信息值,该互信息值越大则表示当前特征图与均值特征图之间的关联程度越强,反之则越弱。而该特征图X对应特征相似度度量系数CFSM的大小反映的是当前冗余特征图X与均值特征矩阵E之间的相似程度,即该范数值越大其相似程度也就越高,反之越低。故而,两者的乘积在一定程度上可以用于衡量当前特征图X与均值特征图E之间特征信息的关联程度,即当CFAC的值偏大时表明当前特征图X与均值特征图E之间特征信息的关联程度高,反之则关联程度低。证毕。
2.1.3 特征融合在筛选出最终的冗余特征集R与表征特征集P之后,便可将冗余特征集R与表征特征集P相融合,构建出下一层的输入特征图Y,具体过程:首先求得R与P中各特征矩阵的特征向量ZR、ZP及特征值λ;接着提出特征融合函数FFC(Z)来融合冗余特征,使用FFC(Z)将R中的冗余特征矩阵融入至P中,构建出融合特征集G;最后合并融合特征集G与表征特征集P,获得最终的输入特征图Y。
定理3(特征融合函数FFC(Z)) 已知有待融合特征矩阵X与Y,两者的融合特征矩阵为Z,则特征融合函数FFC(Z)为
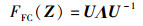
|
(9) |
其中,
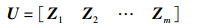
|
(10) |
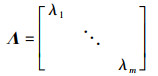
|
(11) |
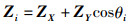
|
(12) |
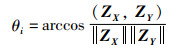
|
(13) |
式中,U为特征向量Zi(i∈[1,m])组合的矩阵,ZX与ZY分别表示特征矩阵X与Y的特征向量,λ1,λ2,…,λm表示特征矩阵X的特征值,θi表示特征向量ZX与ZY的余弦夹角。
证明 已知特征矩阵Y融入特征矩阵X后得到的融合特征矩阵为Z,且特征矩阵Z的特征值与特征向量分别为Zi与λi,则对于特征矩阵Z有:
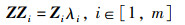
|
(14) |
其中,Zi=ZX+ZYcosθi,ZYcosθi可以表示为特征向量ZY在特征向量ZX上的投影ZY/X,此时对于特征向量Zi有:
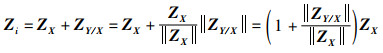
|
(15) |
将Zi代入式(14)可得:
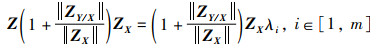
|
(16) |
又因为融合特征矩阵Z的特征值与特征矩阵X的特征值相等,故对于特征向量ZX有:
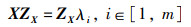
|
(17) |
其中,ZXZX-1=E(E为单位矩阵),此时对于特征向量Zi有:
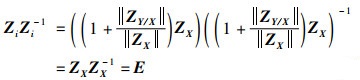
|
(18) |
由式(18)可知特征向量Zi可逆,对式(16)右乘一个Zi-1可得:
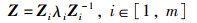
|
(19) |
令特征向量Zi(i∈[1,m])组合为矩阵U,特征值λi(i∈[1,m])构成对角矩阵Λ,即:
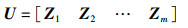
|
(20) |
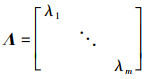
|
(21) |
将式(19)中的m个等式联立可得:
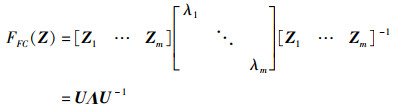
|
(22) |
证毕。
2.2 参数并行更新针对参数更新阶段上卷积运算性能不足的问题,本文结合MapReduce提出了MR-PWC策略,通过使用并行Winograd卷积替代传统卷积的方式来提升模型的卷积运算性能。该策略主要包括3个步骤:特征图切分、并行Winograd卷积和参数更新。
2.2.1 特征图切分为实现Winograd卷积的并行计算,需要先对卷积层的输入特征图进行切分处理,以达到并行计算的需要,因此提出MTS(multiway tree segmentation)策略来并行切分输入特征图,获得各输入特征图的多叉切分树,具体过程为:以原始特征图作为多叉切分树的根节点,首先提出等大小切分函数FESS(X),切分特征图构建出子特征图X11,X12,X21,X22;接着提出等间距切分函数FEDS(X),切分特征图构建出子特征图D;最后将子特征图X11,X12,X21,X22及D作为多叉切分树下一层的子节点,并对上述子节点中的X11,X12,X21,X22执行相同的切分过程,直至无法切分为止便可得到该输入特征图的多叉切分树。
定理4(等大小切分函数FESS(X)) 假设原始特征图X的尺寸为hin×win,卷积核的尺寸为f×f,步长为s,输入特征图被填充后的尺寸为2k×2k,切分后的子特征图X11,X12,X21,X22的尺寸为hsub×wsub,则等大小切分函数FESS(X)为
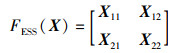
|
(23) |
其中,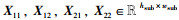
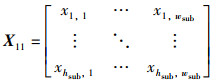
|
(24) |
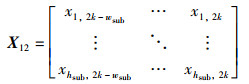
|
(25) |
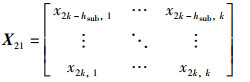
|
(26) |
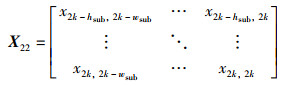
|
(27) |
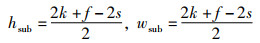
|
(28) |
证明 已知输入特征图X的尺寸为hin×win,填充后的尺寸为2k×2k,卷积核W的尺寸为f×f,步长为s,则对于输入特征图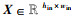
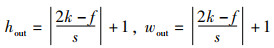
|
(29) |
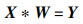
|
(30) |
设切分后子特征图的尺寸为hsub×wsub,其中,
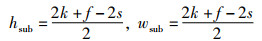
|
(31) |
则对于使用等大小切分函数FESS(X)切分后得到的子特征图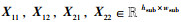
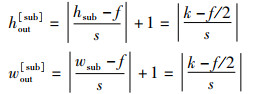
|
(32) |
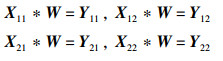
|
(33) |
将式(33)改成矩阵形式可得:
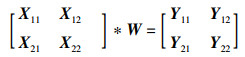
|
(34) |
如上述子特征图X11、X12、X21、X22在矩阵中的位置,对输入特征图X进行相应的切分,并保证各子特征图的尺寸为hsub×wsub,由此可得:
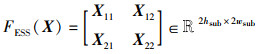
|
(35) |
证毕。
定理5 (等间距切分函数FEDS(X)) 假设原始特征图X的尺寸为hin×win,卷积核的尺寸为f×f,步长为s,左右两侧填充像素块的总数为p0,上下两侧填充像素块的总数为p1,令2k=p0+hin=p1+win,切分后子特征图D的尺寸为2k×2f,则等间距切分函数FEDS(X)为
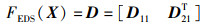
|
(36) |
其中,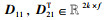
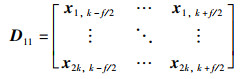
|
(37) |
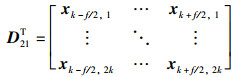
|
(38) |
证明 已知输入特征图X的尺寸为hin×win,填充后的尺寸为2k×2k,卷积核W的尺寸为f×f,步长为s,则对于原始特征图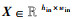
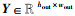
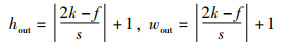
|
(39) |
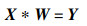
|
(40) |
对于使用等大小切分函数FESS(X)切分后得到的子特征图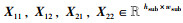
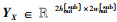
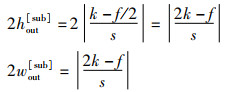
|
(41) |
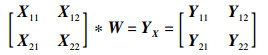
|
(42) |
对比输出特征图Y与输出特征图YX的尺寸可知,当前输出特征图YX的尺寸与输出特征图Y的尺寸仅相差1,为保证卷积后输出特征图的一致性,需要以输入特征图的中点作为切分起点,对输入特征图再进行切分得到子特征图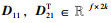
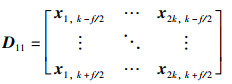
|
(43) |
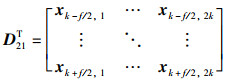
|
(44) |
子特征图D11、D21T经历卷积运算后得到的输出特征图为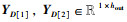
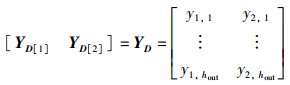
|
(45) |
将输出特征图YD[1]、YD[2]与输出特征图YX合并,合并时将第1列YD[1]作为行向量[y1,1,y1,2, …,y1,hout],第2列YD[2]作为列向量[y2,1,y2,2, …,y2,hout]T,其中,
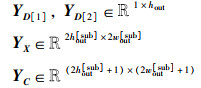
|
再令,
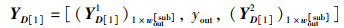
|
(46) |
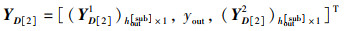
|
(47) |
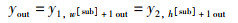
|
(48) |
由此可以得到合并后的输出特征图YC:
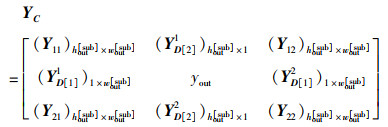
|
(49) |
与输出特征图Y对比可知,该输出特征图YC的结果与输出特征图Y的结果一致,为(2hout[sub]+1)×(2wout[sub]+1),与原始特征图X卷积运算后得到的输出特征图Y的尺寸hout×wout相同,即:
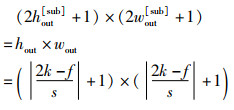
|
(50) |
证毕。
2.2.2 并行Winograd卷积使用MTS策略切分输入特征图得到各特征图的多叉切分树后,便可结合MapReduce实现Winograd卷积的并行卷积计算,该过程主要包含3个步骤:
1) 特征图切分与转换:先并行构建各输入特征图的多叉切分树T,再层级遍历T获得子特征图序列S={Si,i∈[0,n]},在层级遍历的同时对Si∈S与卷积核Wk∈W进行相应的Winograd转换,并将转换后的结果映射成键值对[Si,Wk]存入HDFS中。
2) 并行卷积计算:调用Map()函数并行Winograd卷积计算,首先依据子特征图序列相应的键值对[Si,Wk]计算各子特征图的卷积结果Ysi,k,并将卷积的中间结果映射为键值对[Si,Ysi,k]暂存Combine中;接着调用Reduce()函数并行合并Combine中各子特征图序列的卷积结果Ysi;最后将卷积结果Ysi映射为键值对[Si,Ysi]存入HDFS中。
3) 特征图合并:读取HDFS中各子特征图序列Si∈S的卷积结果[Si,Ysi],并调用Reduce()函数对卷积结果进行并行合并,在得到最终的输出特征图Y后,再将其存入HDFS中供参数更新时使用。
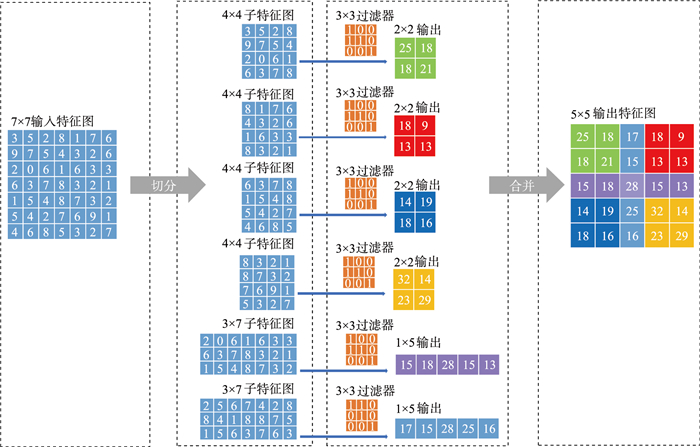
为了更好地描述并行Winograd卷积的运算过程,以输入特征图尺寸为7×7、卷积核尺寸为3×3、步长为1的卷积模型作为示例,对该输入特征图执行并行Winograd卷积的过程示意图如图 1所示。
|
| 图 1 并行Winograd卷积示意图 Fig.1 Schematic diagram of the parallel Winograd convolution |
并行Winograd卷积计算结束后,便可使用反向传播的误差传导公式并行计算各卷积层的误差传导项δ与权值改变量ΔW,实现参数的并行更新,具体过程为:首先根据反向传播公式求得第l-1层卷积核Wkl-1的误差传导项δkl-1,并将结果映射为键值对[Wkl-1,δkl-1]存入HDFS中;接着调用Reduce() 函数合并HDFS中的[Wkl-1,δkl-1]获得第l-1层的δl-1;最后计算出各节点网络模型中Wk的权值改变量ΔWk,并在使用ΔWk更新Wk中的参数后,再将该更新结果映射为[Wk,ΔWk]输出至HDFS中供参数组合阶段使用。
2.3 参数并行合并针对参数组合阶段上参数并行化合并效率低的问题,提出了LB-TM策略,通过均衡各节点之间任务负载的方式提升参数的并行化合并效率。该策略主要包含3个步骤:
1) 统计节点信息,构建信息检索树
首先统计所有任务节点的信息,并依据节点容量升序排序后存入Dnodes数组中;接着,为更快地检索节点信息和调控节点之间的负载,设计了信息检索树IRT(information retrieval tree)来存储任务节点的信息,将Dnodes中的节点信息存入两棵信息检索树HT1与HT2中。
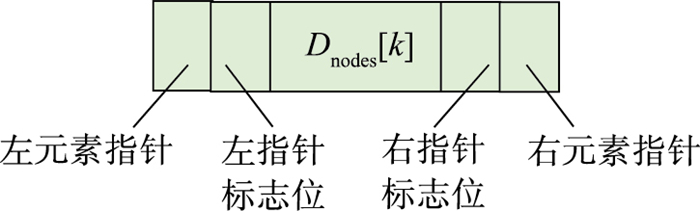
定义4(信息检索树IRT) 信息检索树是一棵具有线索指针的平衡二叉树,树中各节点存储的信息由各任务节点的编号构成,其节点所对应的信息均保存在由以节点编号为索引的数组Dnodes中。IRT树节点的结构体如图 2所示。其中,指针标志位包含3种状态:当标志位为0时表示指针指向的是左、右孩子节点;当标志位为1时表示指针指向的是前驱、后继线索节点;当标志位为2时表示指针指向的是前驱线索与后继线索相连接的节点。
|
| 图 2 IRT树节点的结构体 Fig.2 The node structure of the IRT tree |
信息检索树HT1与HT2的构建步骤:①取得t时刻Dnodes中负载的中位数L0(t),并将其作为节点负载的分界点;②根据分界点L0(t)将Dnodes中节点负载低于L0(t)的存入HT1中,高于L0(t)的存入HT2中;③为了在设定迁移阈值时能够更快地调控节点之间的负载,在存入的过程中,需满足HT1的节点总数始终小于HT2的节点总数的条件,若存入点时不满足该条件,则需将树HT1中超出的节点移入HT2中,并保证HT1中节点的负载总值低于HT2的负载总值;④存入过程结束后,便可对信息检索树HT1与HT2执行树的中序线索化,为了在构建迁移队列时能够快速地检索节点信息,需要将信息检索树HT1与HT2之间的线索相连接,即HT1的第一个前驱线索与HT2的最后一个后继线索相连接,HT2的第一个前驱线索与HT1的最后一个后继线索相连接。
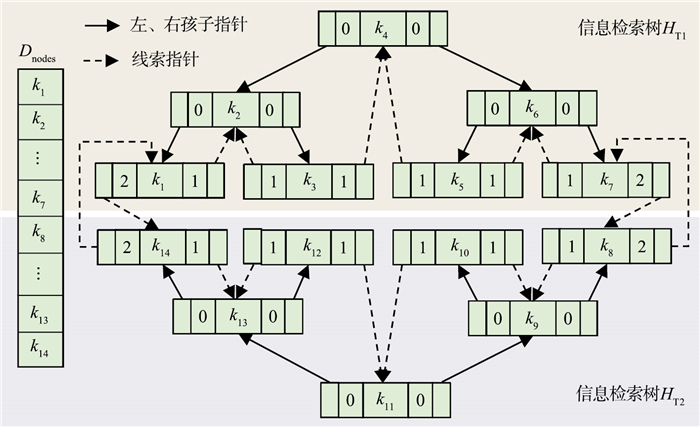
为了能够更清晰地描述信息检索树的构建过程,对节点总数为14且已排序的节点队列Dnodes构建信息检索树HT1与HT2,其构建结果示意图的如图 3所示。
|
| 图 3 IRT树构建结果示意图 Fig.3 The schematic diagram of the constructed IRT tree |
2) 设定迁移阈值,构建迁移队列
构建出信息检索树HT1与HT2之后,便可根据设定好的迁移阈值来构建任务迁移的路线,具体过程为:首先提出动态负载迁移阈值DLMT(dynamic load migration threshold)来动态设定任务迁移的阈值,将HT1的负载迁入上限设为Lα(t),HT2的负载迁出下限设为Lβ(t);接着构建任务迁移的路线,先从树HT1中取得负载率最低的节点Nmin,并从树HT2中取得负载率最高的节点Nmax之后,再构建相应的迁移路线,若节点Nmin与节点Nmax的负载均满足迁移阈值,则将迁移路线[Nmax,Nmin]存入迁移队列Q中;否则放弃该迁移路线,并重复上述构建过程,直至HT1与HT2中没有满足阈值的节点。
定理6(动态负载迁移阈值DLMT) 假设t时刻信息检索树HT1与HT2中负载的中位数分别为Lm1(t)和Lm2(t),HT1与HT2各自的负载均值为L1(t)和L2(t),动态负载迁移阈值中迁入上限与迁出下限分别为Lα(t)与Lβ(t),则动态负载迁移阈值为
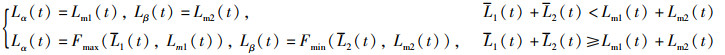
|
(51) |
其中,Fmax(·)与Fmin(·)分别表示两数间最大值函数与两数间最小值函数。
证明 已知信息检索树HT1与HT2都是平衡二叉树,且两者之间的节点个数相差不超过1,因此当两棵树中负载的中位数与各自的负载均值越接近,两棵树中的节点负载就会越趋近集群总体的负载均值L(t),即:
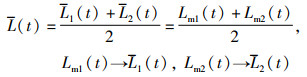
|
(52) |
当L1(t)+L2(t) < Lm1(t)+Lm2(t)时,集群总体的负载均值低于负载中位数,此时集群处于负载不均衡的状态,将HT1的迁入上限调整为Lm1(t),HT2的迁出下限为Lm2(t),并对HT1与HT2进行任务迁移后,便可以使HT1与HT2集群两部分的负载均值往负载中位数靠近,促使集群达到负载均衡的目标。当L1(t)+L2(t)≥Lm1(t)+Lm2(t)时,集群总体趋于负载均衡,但是集群中仍存在部分负载不均衡的节点,此时将HT1的迁移上限调整为均值L1(t)与中位数Lm2(t)之间的最大值,将HT2的迁移下限调整为均值L2(t)与中位数Lm2(t)之间的最小值,执行任务迁移后便可以使HT1与HT2集群两部分的负载均值相互靠近以达到负载均衡的目标。综上,动态负载迁移阈值DMLT可以调控集群中各节点任务迁移的方向,确保集群总体达到负载均衡。证毕。
3) 执行迁移任务,并行参数组合
构建完迁移队列Q后便可执行迁移任务,待到迁移任务结束后再调用Reduce()函数并行合并参数,具体过程为:首先从Q中取出队首节点〈Nfrom,Nto〉,依据当前迁移路线与迁移阈值从节点Nfrom中迁出未处理的任务发送给节点Nto,若任务迁移过程中节点Nfrom与节点Nto有一方到达迁移阈值,则会结束当前迁移任务;接着计算t时刻HT1与HT2中节点的负载均值L1(t)与L2(t),若出现L1(t)+L2(t) < Lα(t)+Lβ(t),则会结束本次迁移过程,否则接续执行Q中的迁移任务,直至迁移队列为空;最后调用Reduce()函数对各Map节点输出的键值对〈Wk,ΔWk〉进行并行合并,并将合并后的权值作为DCNN模型训练后的最终权值。
2.4 算法时间复杂度分析DC-CNN算法[9]采用并行计算的方式实现了模型的并行化训练过程,相较于单机器的训练方式,具有更高的训练效率;MR-PCNN算法[10]设计参数的并行更新策略提升了模型参数的并行更新效率,具有较高的参数更新效率;MR-MPC算法[11]通过并行化矩阵乘法运算替换传统卷积运算的思想提高了卷积的运行效率,具有良好的卷积运算性能;MR-CNN算法[12]引入集中式参数服务器的思想实现了各节点之间模型参数更新的共享,具有较好的参数并行化合并效率。由于IA-PDCNNOA算法[13]相较于WP-DCNN算法在冗余特征的筛选上存在滤波与过滤无法有效并行的缺陷,因此,本文仅选取DC-CNN、MR-PCNN、MR-MPC及MR-CNN算法与WP-DCNN算法进行时间复杂度分析和实验对比。
WP-DCNN算法的时间复杂度主要由冗余特征筛选、参数并行更新和参数并行合并三个部分构成,分别记为T1、T2、T3。
1) 冗余特征筛选阶段:该阶段的时间复杂度主要由特征划分、特征过滤和特征融合三部分组成。假设特征划分后采样特征集和候选特征集的大小分别为s和c,特征过滤时冗余特征集和表征特征集大小分别为r和p,迭代过滤次数为q,特征融合时融合特征矩阵的尺寸为wf×hf,且wf < hf,由此可得冗余特征筛选阶段的时间复杂度T1为
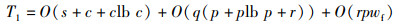
|
(53) |
2) 参数并行更新阶段:该阶段的时间复杂度主要由特征图划分、并行Winograd卷积和特征图合并三个部分组成。特征图划分的时间复杂度取决于等大小切分函数FESS(X)和等间距切分函数FEDS(X)的时间复杂度,假设输入特征图被填充后的尺寸为2k×2k,且经历等大小切分函数FESS(X)切分后的子特征图的最小尺寸为m×m,则特征图划分的时间复杂度为O((4h-1)/3)+O(h),其中h=|lb(2k/m)|;在并行Winograd卷积时,已知执行一次F(m×m,k×k)的时间复杂度为O((1+β+γ+δ)(m-k+1)2),其中β、γ和δ分别为Winograd转换时对单个图块使用的浮点指令数,则并行Winograd卷积的时间复杂度为O((4h+h)·(1+β+γ+δ)(m-k+1)2);特征图合并是根据多叉切分树的序列结构从下往上对输出特征图进行多路合并,因此其时间复杂度为O((4(h-1)-1)/3)。综上,参数并行更新阶段的时间复杂度T2为
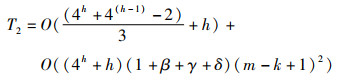
|
(54) |
3) 参数并行合并阶段:该阶段的时间复杂度主要取决于信息检索树的构建和更新。在构建信息检索树时,需要先对含有d个节点信息的数组进行排序后才能进行信息检索树的构建,构建结束后还需对信息检索树进行一遍中序线索化,因此构建信息检索树的时间复杂度为O(dlb d)+O(dlb (d/2))+O(d);在执行完迁移任务后,各任务节点的负载都发生了相应的变化,此时需要重新对信息检索树进行更新操作,假设任务迁移队列的长度为b,则更新信息检索树的时间复杂度为O(blb (b/2))。综上,参数并行合并阶段的时间复杂度T3为
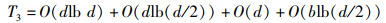
|
(55) |
综上可知,WP-DCNN算法的时间复杂度为
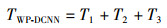
|
(56) |
在大数据环境下训练DCNN模型的时间复杂度主要取决于批训练阶段与参数并行更新阶段中的卷积计算,因此可以得知,T2的时间复杂度远远大于T1与T3,即T2≫T1,T3。假设计算节点的个数为u,网络模型包含D个卷积层,且第l个卷积层的卷积核数量为Cl、输入特征图的尺寸为Ml×Ml、卷积核的尺寸为Kl×Kl,则使用传统卷积进行模型训练时的时间复杂度为
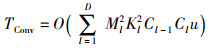
|
(57) |
使用Winograd卷积进行模型训练时的时间复杂度为
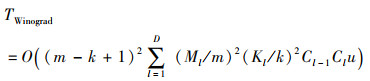
|
(58) |
使用并行矩阵乘法进行模型训练时的时间复杂度为
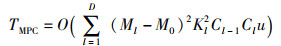
|
(59) |
其中,M0为矩阵乘法运算中零元素的个数。
对于DC-CNN[9]、MR-PCNN[10]和MR-CNN[12]算法,由于这些算法在模型训练上使用的均是传统卷积算法,并且在模型批训练阶段并未对特征图进行有效的筛选,致使这些算法在参数并行更新阶段的时间复杂度远高于WP-DCNN算法,即T2-DC-CNN≫T2-WP-DCNN,T2-MR-PCNN≫T2-WP-DCNN,T2-MR-CNN≫T2-WP-DCNN。而对于MR-MPC[11]算法,该算法在参数并行更新阶段采取了并行矩阵乘法替换传统卷积的方式来提升卷积运算效率,但是该并行矩阵乘法策略在高计算密度的训练过程中对于卷积运算效率的提升有限,致使该算法在模型训练上的时间复杂度仍低于WP-DCNN算法,即TConv>TMPC>TWinograd。综上,相较于DC-CNN、MR-PCNN、MR-MPC和MR-CNN算法,WP-DCNN算法具有更低的时间复杂度。
3 实验结果与分析 3.1 实验环境为验证WP-DCNN算法的性能,设计了相关实验。在硬件方面,本实验设置了8个计算节点,其中包含1个Master节点与7个Slaver节点。各计算节点的硬件配置均为IntelⓇ CoreTM i7-10750H CPU、16GB DDR4 RAM、1TB SSD且各节点处于同一局域网内,并通过1 Gb/s以太网进行通信。在软件方面,每个计算节点上的软件配置均为Ubuntu 16.04.7、Hadoop 2.7.7、JDK 1.8.0。集群中各计算节点的具体配置如表 1所示。
| 节点类型 | 主机名 | IP地址 |
| Master | Master | 192.168.101.1 |
| Slaver | Slaver_1~ Slaver_7 | 192.168.101.2~192.168.101.8 |
该实验采用4个真实数据集,分别是CIFAR-10[19]、CIFAR-100[20]、SVHM[21]和Emnist-Balanced[22]。CIFAR-10是由60 000张彩色图像构成的一个数据集,该数据集总共分为10类,每个类包含6000张图像;CIFAR-100与CIFAR-10相似,但它包含100类,每个类包含600张图像;SVHM(street view house number)是摘自于Google街景门牌号码的一个数据集,该数据集总共分为10类;Emnist-Balanced是源自NIST特殊数据库19的一个手写字符数字数据集,该数据集总共分为47类。各数据集的详细信息如表 2所示。
| 数据集 | 图片数/张 | 图像大小/像素 | 类别数/类 | 数据特点 |
| CIFAR-10 | 60 000 | 32×32 | 10 | 类别少,样本多 |
| CIFAR-100 | 60 000 | 32×32 | 100 | 类别多,样本少 |
| SVHM | 73 200 | 32×32 | 10 | 类别少,训练样本多 |
| Emnist-Balanced | 131 600 | 28×28 | 47 | 类别多,训练样本多 |
1) 加速比
加速比是指同一个任务在串行系统和并行系统中执行所需时间的比率,可用于衡量并行算法在并行系统中并行化处理的性能,其定义为
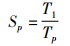
|
(60) |
其中,p为计算节点的个数,T1、Tp分别为在第1个、第p个计算节点下执行算法所需的时间。Sp越大表明算法的并行化性能越高。
2) 准确率
准确率是指分类模型正确分类的样本数与总样本数的比值,可用于衡量分类算法的分类性能,其定义为
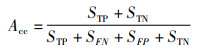
|
(61) |
其中,STP、STN、SFP、SFN分别对应混淆矩阵中将正类样本预测为正类的样本数、将正类样本预测为负类的样本数、将负类样本预测为正类的样本数与将负类样本预测为正类的样本数。Acc的值越大代表该分类模型的分类效果越好。
3) 吞吐量
吞吐量是指单位时间内处理器执行浮点运算的次数,可用于衡量卷积算法的卷积运算性能,其定义为
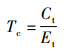
|
(62) |
其中,Tc的单位为FLOPS(floating point operations per second);Ct表示该DCNN模型的浮点计算总数,其单位为FLOPs(floating point operations);Et表示运行该算法的总执行时间,单位为s。Tc的值越大表明该算法的加速性能越好。
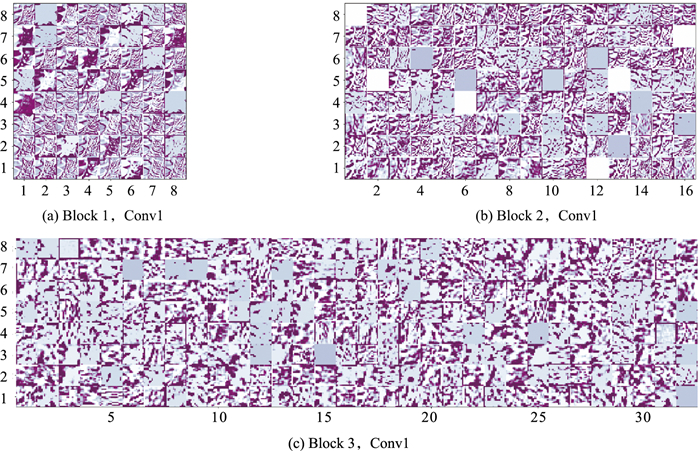
3.4 算法可行性比较分析 3.4.1 FF-CSNMI策略的可行性分析为了分析FF-CSNMI策略在并行训练DCNN模型上的性能,分别可视化了使用FF-CSNMI策略与不使用FF-CSNMI策略训练的VGG-16模型在Block 1、Block 2和Block 3的第1个卷积层(Conv1)上的特征图,可视化结果如图 4和图 5所示。
|
| 图 4 训练VGG-16不使用FF-CSNMI策略 Fig.4 Training VGG-16 without FF-CSNMI strategy |

|
| 图 5 训练VGG-16使用FF-CSNMI策略 Fig.5 Training VGG-16 with FF-CSNMI strategy |
从图 4和图 5可以看出,使用FF-CSNMI策略后各卷积层上特征图的特征信息较不使用FF-CSNMI策略时的特征信息更为丰富,并且随着网络的深入,FF-CSNMI策略提取特征信息的性能更为显著。图 5(a)上各特征图的特征信息都较为清晰,并且其特征信息中的明暗交界线相较于图 4(a)都较为平缓;图 4(b)和图 4(c)上存在着特征信息空白或特征信息较少的特征图,而图 5(b)和图 5(c)上各特征图的特征信息都较为丰富,并且随着网络层次的深入,FF-CSNMI策略提取到的特征信息更加地有效和集中。产生该现象的原因是:FF-CSNMI策略凭借特征划分与特征过滤使得提取到的特征信息更为有效与集中,而特征融合则提升了WP-DCNN算法在批训练过程上提取特征信息的能力。综上,FF-CSNMI策略具有可行性,且使用FF-CSNMI策略能够显著提升WP-DCNN算法提取特征信息的性能。
3.4.2 MR-PWC策略的可行性分析为验证MR-PWC策略的卷积运算性能,以吞吐量作为评价指标,在VGG-16卷积层上分别对比了3种卷积算法:普通卷积算法、传统Winograd卷积算法(Winograd)和本文提出的MR-PWC策略。为避免实验的偶然性,实验以各卷积算法在VGG-16卷积层上独立运行10次总执行时间的均值来计算各卷积层上的吞吐量。实验结果如图 6所示。

|
| 图 6 3种卷积算法的吞吐量 Fig.6 The throughput of three convolution algorithms |
从图 6可以看出,MR-PWC策略在VGG-16卷积层上的卷积运算性能显著高于普通卷积算法和传统Winograd卷积算法。如图 6所示,MR-PWC策略在VGG-16卷积层上所达到的平均吞吐量最高,达到了641.04,分别是普通卷积算法和传统Winograd卷积算法的2.34倍和1.31倍。出现这种现象的原因是:1) MR-PWC策略是通过并行Winograd卷积运算替换传统卷积运算的方式来加速卷积结果的生成,相较于普通卷积算法,其卷积运算性能更高;2) MR-PWC策略结合了并行计算框架MapReduce与Winograd卷积,相较于传统Winograd卷积算法,其Winograd转换过程是通过并行化的方式实现的,在较大程度上提升了Winograd卷积的运算效率,使得该卷积加速策略的加速性能更优于传统Winograd卷积算法。综上,MR-PWC策略具有可行性,且相较于普通卷积算法和传统Winograd卷积算法拥有更显著的卷积运算性能。
3.5 算法性能比较分析 3.5.1 分类效果为评估WP-DCNN算法的分类效果,以准确率作为评价指标,将WP-DCNN算法分别与DC-CNN[9]、MR-PCNN[10]、MR-MPC[11]和MR-CNN[12]算法在上述4个数据集上进行了对比实验。实验结果如图 7所示。

|
| 图 7 各算法在4个数据集上训练时的准确率 Fig.7 The accuracy of each algorithm on the four datasets |
从图 7可以看出,随着训练轮数的不断增加,各算法的分类准确率逐渐上升并趋于平稳,而WP-DCNN算法在4种数据集上的最终准确率均高于其他4种算法,并且WP-DCNN算法分类准确率趋于平稳时所需的训练轮数始终低于其他4种算法。其中,在处理数据集CIFAR-10上,如图 7(a)所示,当训练轮数为25次时,WP-DCNN算法的分类准确率已经趋于平稳,并且比同等训练轮数下的DC-CNN、MR-PCNN、MR-MPC和MR-CNN算法的分类准确率分别高出了4.62%、4.22%、3.09%、2.45%;在处理数据集CIFAR-100上,如图 7(b)所示,WP-DCNN算法的分类准确率趋于平稳所需的训练轮数为30次,比DC-CNN和MR-PCNN算法趋于平稳的训练轮数少了10次,比MR-MPC和MR-CNN算法趋于平稳的训练轮数少了5次;在处理数据集SVHN和Emnist-Balanced上,如图 7(c)和7(d)所示,WP-DCNN算法的分类准确率趋于平稳所需的训练轮数显著低于其他4种算法,而且在同等训练轮数下WP-DCNN算法的分类准确率始终保持最高。产生这种结果的原因是:1) WP-DCNN算法凭借FF-CSNMI策略消除了冗余特征在批训练过程中的重复计算,提升了算法的训练效率,同时也在一定程度上提升了算法的分类精度;2) WP-DCNN算法凭借MR-PWC策略有效提升了卷积的运算性能,进一步提升了算法的训练效率。综上,WP-DCNN算法相较于其他算法具有更优秀的分类性能。
3.5.2 算法运行时间为验证WP-DCNN算法的时间复杂度,在上述4个数据集上对DC-CNN[9]、MR-PCNN[10]、MR-MPC[11]和MR-CNN[12]算法分别进行了5次测试,并取5次运行时间的均值作为最终的实验结果。实验结果如图 8所示。

|
| 图 8 各算法在4个数据集上的运行时间 Fig.8 The runtime of each algorithm on the four datasets |
从图 8可以看出,在对各数据集进行处理时,WP-DCNN算法的运行时间始终保持最短,并且随着数据规模的不断上升,WP-DCNN算法的运行时间与其他4种算法的运行时间的比例也逐渐扩大。其中,当处理数据量较小的数据集CIFAR-10时,WP-DCNN算法运行时间的占比分别是DC-CNN、MR-PCNN、MR-MPC和MR-CNN算法的1.42倍、1.25倍、1.31倍和1.15倍;当处理数据量较大的数据集Emnist-Balanced时,WP-DCNN算法运行时间的占比分别是DC-CNN、MR-PCNN、MR-MPC和MR-CNN算法的1.85倍、1.67倍、1.74倍和1.42倍。产生这种结果的原因是:1) WP-DCNN算法凭借FF-CSNMI策略消除了冗余特征的重复计算,降低了算法在冗余特征计算上的时间开销;2) MR-PWC策略提升了算法的卷积运算性能,降低了算法在卷积计算上的时间开销,并且随着数据规模的不断扩增,MR-PWC策略在卷积运算上的并行化性能得到了进一步提升,使得WP-DCNN算法相较于其他算法拥有更加优秀的处理能力。因此,WP-DCNN算法所需的运行时间最短,而且随着数据规模的增长,其运行时间与其他4种算法运行时间的比例也在逐步扩大。综上,WP-DCNN算法相较于其他算法在处理大数据集上具有更出色的性能。
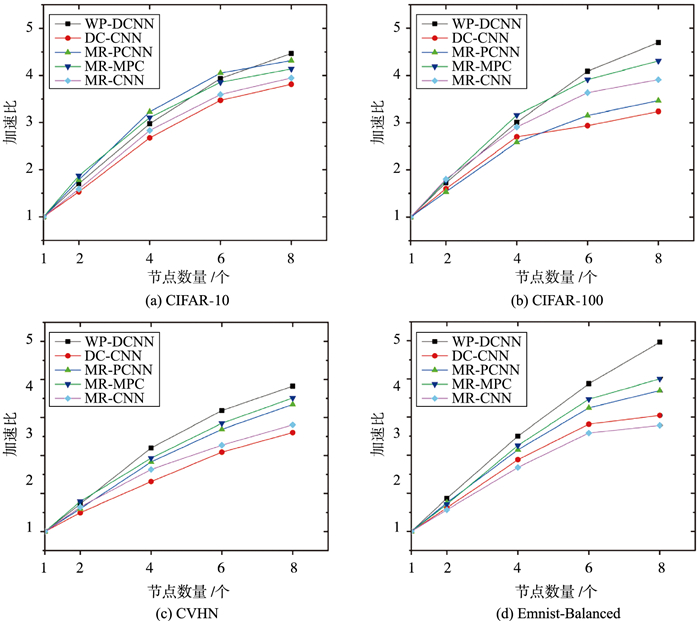
3.5.3 算法加速比为评估WP-DCNN算法在大数据环境下的并行性能,在上述4个数据集上对DC-CNN[9]、MR-PCNN[10]、MR-MPC[11]和MR-CNN[12]算法分别进行了5次测试,并取均值来计算各算法在不同计算节点个数下的加速比。实验结果如图 9所示。
|
| 图 9 各算法在4个数据集上的加速比 Fig.9 The speedup of each algorithm on the four datasets |
从图 9可以看出,在处理CIFAR-10,CIFAR-100,SVHN和Emnist-Balanced数据集时,各算法在4个数据集上的加速比随着节点数量的增加而逐渐上升,并且随着数据规模的逐步扩大,WP-DCNN算法在各数据集上的加速比远超其他4种算法。其中,在处理数据规模较小的数据集CIFAR-10上,如图 9(a)所示,各算法之间的加速比相差不大,当节点数量为2时,WP-DCNN算法的加速比为1.705,分别比MR-PCNN算法和MR-MPC算法的加速比低了0.081、0.168,比DC-CNN算法和MR-CNN算法的加速比高了0.173、0.115;当节点数量增加至8时,WP-DCNN算法的加速比却超过了其他4种算法,分别比DC-CNN、MR-PCNN、MR-MPC和MR-CNN算法的加速比高出了0.655、0.149、0.328、0.520。产生这种结果的原因是:1) 当节点数量较小时,各节点间的通信时间占算法总体运行时间的比例很大,而且采用并行计算提升的运算效率有限,不足以弥补并行计算时各节点所消耗的通信时间,由此导致WP-DCNN算法所得的加速比较小;2) 当节点数量增加时,WP-DCNN算法凭借LB-TM策略有效调节了各节点之间的负载,提升了各计算节点的并行运算效率,使得WP-DCNN算法的加速比略高于其他4种算法。在处理数据规模较大的数据集SVHN和Emnist-Balanced上,如图 9(c)和图 9(d)所示,随着节点数量的不断增长,其他4个对比算法的加速比逐渐趋于稳定,WP-DCNN算法的加速比则逐渐上升,尤其是在处理数据集Emnist-Balanced上,WP-DCNN算法的加速比总体上接近线性增长且始终拥有最高的加速比。产生这种结果的原因是:1) LB-TM策略通过均衡各节点间的负载提升了WP-DCNN算法的并行计算性能,在一定程度上弥补了节点间通信时间的开销;2) MR-PWC策略通过提升卷积的运算性能有效降低了WP-DCNN算法总体的运行时间,而且随着数据规模的扩大,MR-PWC策略通过高效的并行化Winograd卷积运算来降低算法总体运行时间的优势也被逐渐放大。综上,WP-DCNN算法相较于其他算法具有更好的并行性能。
4 结语为克服大数据环境下并行DCNN算法在模型训练上的不足,提出了一种基于Winograd卷积的并行深度卷积神经网络优化算法WP-DCNN。首先,提出了FF-CSNMI策略来消除批训练过程中冗余特征的计算,解决了训练过程中冗余特征计算过多的问题;然后,结合MapReduce提出了MR-PWC策略,通过使用并行Winograd卷积运算的方式来提升卷积的运算性能,解决了批训练过程中卷积运算性能不足的问题;最后,提出了LB-TM策略来均衡集群中各任务节点之间的负载,降低了集群总体的平均反应时长,从而提升了训练过程中参数并行化合并的效率。实验表明,WP-DCNN算法显著降低了DCNN模型在大数据环境下的训练代价,而且对并行DCNN的训练效率也有大幅提升。
虽然WP-DCNN算法在大数据环境下表现出良好的训练性能,但算法在特征过滤策略FF-CSNMI上仍存在特征划分比例不合理、特征过滤效果不明显以及特征融合效率不理想等问题,这些不足之处将成为以后研究的重点。此外,未来也将尝试对MR-PWC策略的卷积运算性能做进一步的优化,使其能充分适应大数据集下的卷积运算。
数据可用性声明
与本研究相关的算法伪代码已在中国科学院科学数据银行(Science Data Bank)ScienceDB平台公开发布,访问地址为https://doi.org/10.57760/sciencedb.j00142.00004或https://cstrcn/31253.11.sciencedb.j00142.00004。
| [1] |
TULBURE A A, TULBURE A A, DULF E H. A review on modern defect detection models using DCNNs - Deep convolutional neural networks[J]. Journal of Advanced Research, 2022, 35: 33-48. DOI:10.1016/j.jare.2021.03.015 |
| [2] |
CHAKRABORTY R, PRAMANIK A. DCNN-based prediction model for detection of age-related macular degeneration from color fundus images[J]. Medical & Biological Engineering & Computing, 2022, 60. |
| [3] |
SONG W, FU C, ZHENG Y, et al. Protection of image ROI using chaos-based encryption and DCNN-based object detection[J]. Neural Computing and Applications, 2022, 34: 5743-5756. DOI:10.1007/s00521-021-06725-w |
| [4] |
辛菁, 姚雨蒙, 程晗, 等. 基于卷积神经网络的机器人对未知物体视觉定位控制策略[J]. 信息与控制, 2018, 47(3): 355-362. XIN J, YAO Y M, CHENG H, et al. Vision-based robot positioning control strategy for unknown objects using convolutional neural network[J]. Information and Control, 2018, 47(3): 355-362. |
| [5] |
HOSSAIN M, TALUKDER M, RAHMAN A, et al. Depression prognosis using natural language processing and machine learning from social media status[J]. International Journal of Electrical & Computer Engineering, 2022, 12(3): 2088-8708. |
| [6] |
Mishra A K, Roy P, Bandyopadhyay S, et al. Achieving highly efficient breast ultrasound tumor classification with deep convolutional neural networks[J]. International Journal of Information Technology, 2022, 14(1): 3311-3320. |
| [7] |
ALBDAIRI A J A, XIAO Z, ALKHAYYAT A, et al. Face recognition based on deep learning and FPGA for ethnicity identification[J/OL]. Applied Sciences, 2022[2022-01-09]. https://www.mdpi.com/2076-3417/12/5/2605. DOI: 10.3390/app12052605.
|
| [8] |
NAEEM M, JAMAL T, DIAZ-MARTINEZ J, et al. Trends and future perspective challenges in big data[M]//Advances in Intelligent Data Analysis and Applications. Berlin, Germany: Springer, 2022: 309-325.
|
| [9] |
BASIT N, ZHANG Y, WU H, et al. MapReduce-based deep learning with handwritten digit recognition case study[C]//2016 IEEE International Conference on Big Data. Piscataway, USA: IEEE, 2016: 1690-1699.
|
| [10] |
LEUNG J, CHEN M. Image recognition with MapReduce based convolutional neural networks[C]//10th Annual Ubiquitous Computing, Electronics & Mobile Communication Conference. Piscataway, USA: IEEE, 2019: 119-125.
|
| [11] |
WANG Q, ZHAO J, GONG D, et al. Parallelizing convolutional neural networks for action event recognition in surveillance videos[J]. International Journal of Parallel Programming, 2017, 45(4): 734-759. DOI:10.1007/s10766-016-0451-4 |
| [12] |
LI B, HU X. Effective vehicle logo recognition in real-world application using mapreduce based convolutional neural networks with a pre-training strategy[J]. Journal of Intelligent & Fuzzy Systems, 2018, 34(3): 1985-1994. |
| [13] |
胡健, 龚克, 毛伊敏, 等. 基于Im2col的并行深度卷积神经网络优化算法[J]. 计算机应用研究, 2022, 39(10): 2950-2956, 2961. HU J, GONG K, MAO Y M, et al. Parallel deep convolution neural network optimization based on Im2col[J]. Application Research of Computers, 2022, 39(10): 2950-2956, 2961. |
| [14] |
LU G, ZHOU L. Localization of prostatic tumor's infection based on normalized mutual information MRI image segmentation[J]. Journal of Infection and Public Health, 2021, 14(3): 432-436. DOI:10.1016/j.jiph.2019.08.011 |
| [15] |
RAJ M, TIWARI P, GUPTA P. Cosine similarity, distance and entropy measures for fuzzy soft matrices[J]. International Journal of Information Technology, 2022, 14: 2219-2230. DOI:10.1007/s41870-021-00799-4 |
| [16] |
孙小琳, 季伟东, 王旭. 基于余弦相似度反向策略的自然计算方法[J]. 信息与控制, 2022, 51(6): 708-718. SUN X L, JI W D, WANG X. Natural computation method based on cosine similarity opposition strategy[J]. Information and Control, 2022, 51(6): 708-718. |
| [17] |
ALAM S A, ANDERSON A, BARABASZ B, et al. Winograd convolution for deep neural networks: Efficient point selection[EB/OL]. (2022-01-25)[2022-06-01]. https://arxiv.org/abs/2201.10369v1.
|
| [18] |
ALAM S A, ANDERSON A, BARABASZ B, et al. Winograd convolution for deep neural networks: Efficient point selection[J]. ACM Transactions on Embedded Computing Systems, 2022, 21(6): 1-28. |
| [19] |
DIVYA S, ADEPU B, KAMAKSHI P. Image enhancement and classification of CIFAR-10 using convolutional neural networks[C/OL]//4th International Conference on Smart Systems and Inventive Technology. Piscataway, USA: IEEE, 2022[2022-04-06]. https://ieeexplore.ieee.org/document/9716555. DOI: 10.1109/ICSSIT53264.2022.9716555.
|
| [20] |
HONG T P, HU M J, YIN T K, et al. A multi-scale convolutional neural network for rotation-invariant recognition[J/OL]. Electronics. [2022-04-08]. https://www.mdpi.com/2079-9292/11/4/66. DOI: 10.3390/electronics11040661.
|
| [21] |
LI K, YE W. Semi-supervised node classification via graph learning convolutional neural network[J]. Applied Intelligence, 2022, 52(11): 12724-12736. DOI:10.1007/s10489-022-03233-9 |
| [22] |
AL-ARINI M, AL-HAFIZ F, AMASH S. Character recognition from images using a convolutional neural network[C]//Sixth International Congress on Information and Communication Technology. Berlin, Germany: Springer, 2022: 403-413.
|



