0 引言
近年来,形式简单、动力学行为丰富的忆阻混沌系统及其几何控制受到了许多学者的关注。几何控制包括振幅控制[1-3]、频率控制[4]和偏移增量控制[5-6]。基于状态变量的偏移增量控制,通常是指从单个状态变量中减去一个常数,使得混沌吸引子沿坐标轴移动,且一些混沌系统可以通过控制参数或改变初值的方法来获得无穷多共存吸引子[7-9],称这类系统具有超级多稳态[10]。依赖于初始值的多稳态[11-12]通常是非线性、非单调和多维的。
忆阻器[13-15]具有许多优异的特性,如低能耗和非易失性。具有忆阻器的系统更可能具有超混沌、暂态混沌、无平衡点、线平衡[16-17]或平面平衡等特征,许多忆阻混沌系统初始值取一定的间隔时,吸引子会发生偏移或旋转。由于其丰富的动力学行为,具有超级多稳态的混沌系统能在电路实现、同步、图像加密和其他物理或工程领域获得更丰富的应用。获得忆阻混沌系统的常用方法,通常是在混沌系统中添加忆阻器元件,或将忆阻器方程乘到现有的项中。例如,王梦娇[18]将一个二次忆阻器加到一个5维(5D)混沌系统中,得到了5D忆阻混沌系统,它具有基于忆阻变量初值的旋转共存吸引子;MEZIONA[19]通过将忆阻器方程乘到一个超混沌系统的线性项中,提出了一个6D超混沌系统,当选择的参数不同时,系统会从线平衡变为面平衡;武花干[20]通过使用两个忆阻器耦合来代替两个电阻器耦合,提出了一个超混沌系统;秦铭宏[21]将整个忆阻输出项作为负反馈控制引入到一个3维系统中,并扩展成4维混沌系统,得到了一个具有无穷共存吸引子的简单忆阻混沌系统,且发现该系统在不同的参数下,能够产生丰富的混沌吸引子与周期吸引子;李晓霞[22]使用一个磁控忆阻器替换改进的4维Lü混沌系统中的耦合参数,提出和分析了一个新的具有超级多稳态和条件对称的五维忆阻超混沌系统。
一般来说,形式简单的混沌系统动力学行为往往也比较单一,因此构造出形式简单且动力学行为丰富的混沌系统具有重要的意义。与一些类似系统进行比较发现,本文提出的5维超混沌系统仅有10项,却具有更丰富的动力学特性,如表 1所示。
具有超级多稳态的混沌系统因其有多种正常运行状态,是目前的一个研究热点。而本文提出的具有隐藏超级多稳态的高维混沌系统,可以产生更复杂和难以预测的运动轨迹,在混沌保密通信中有更高的应用价值。关于多稳态,大量文献讨论的内容是初值沿平行于坐标轴方向移动时,混沌系统的各种不同吸引子类型[22]或绘制初始值在平面内的吸引域[23-24]。本文不仅演示了当x(0)和u(0)单独变化时,系统具有的超级多稳态特性,又进一步探讨了当初始值沿着x-u平面的不平行于坐标轴的直线移动过程中,吸引子的偏移动方向和偏移幅度,揭示了一些新的现象。
基于以上实验和研究,本文通过在4维超混沌系统中添加一个光滑的二次磁控忆阻器,提出一个项数较少、形式简单的5维忆阻超混沌系统;给出了系统在参数影响下的变化过程;基于相图、分岔图、李雅普诺夫指数谱和状态变量随参数变化时的均值,分析了状态变量u、z的偏移行为,演示了参数变化下系统状态变量的幅值控制;在研究初值沿不同直线变化过程中,对吸引子的偏移方向和偏移幅度进行了定量分析。最后,忆阻混沌电路在示波器上的演示结果,进一步证明了忆阻超混沌系统的存在性。
1 5维超混沌系统的提出 1.1 模型的描述方程(1)是一个光滑忆阻器:
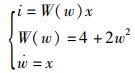
|
(1) |
当a=0.1时,方程(2)是一个4维超混沌系统:
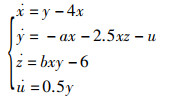
|
(2) |
将W(w)作为负反馈控制项引入到超混沌系统(2)中,得到了一个具有丰富动力学行为的5D混沌系统(3),它有10项,非线性项只有3项。
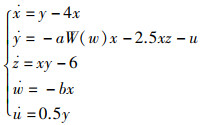
|
(3) |
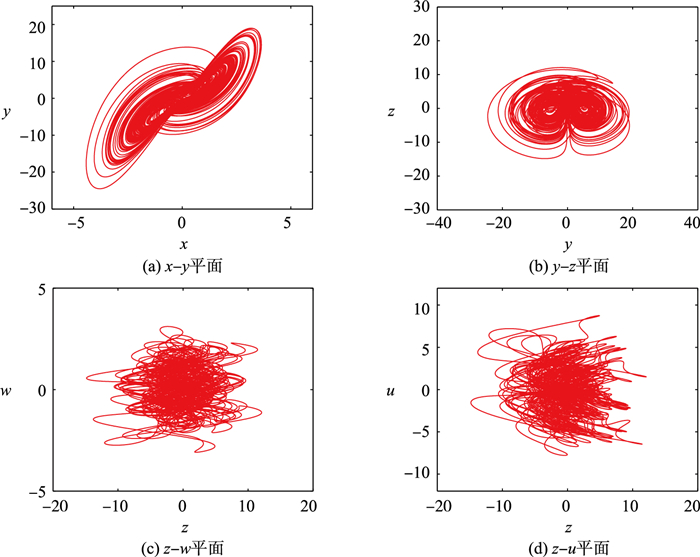
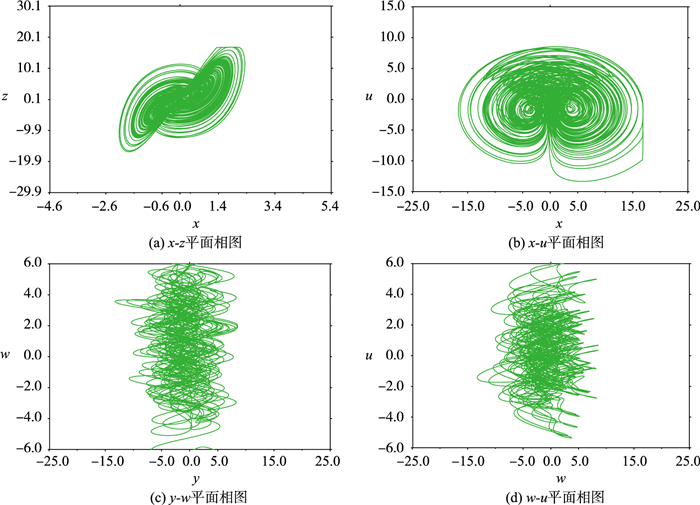
其中,a为耦合强度,当参数a=0.1,b=0.8且初始值均为0.1时,系统(3)的李雅普诺夫指数值为LE1=0.216 6,LE2=0.023,LE3=0,LE4=-0.004,LE5=-4.238。显然,当取上述一组参数和初始值时,系统(3)是超混沌系统,很好地表现出丰富的动力学行为。图 1是系统(3)在4个平面上的相图。
|
| 图 1 a=0.1,b=0.8时系统(3)的平面相图 Fig.1 Phase plane diagrams of system (3) with a=0.1, b=0.8 |
令系统(3)中状态变量的导数等于0,得方程(4):
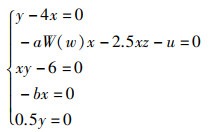
|
(4) |
从方程(4)的第4和第5个方程中,可以得到x=0且y=0,而由第3个方程可知xy=6,这产生了矛盾,因此,方程(4)无解,系统(3)没有平衡点,因此,系统(3)具有隐藏吸引子。
1.3 系统的对称性系统(3)在坐标变换(x,y,z,w,u) → (-x,-y,z,-w,-u)下具有对称性。当在一对对称初始值下进行坐标变换时,状态变量沿每个坐标轴的变化率相同或相反,因此,可以观测到对称或旋转的共存吸引子。
1.4 耗散性系统(3)的散度:
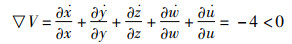
|
(5) |
这意味着系统(3)是耗散的。
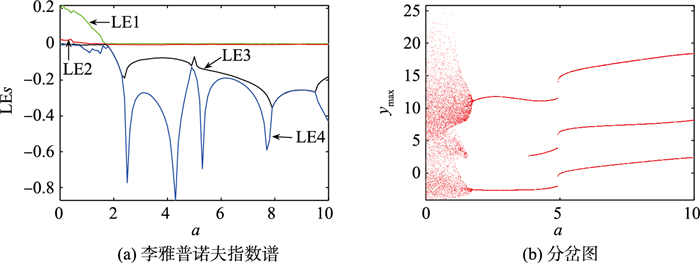
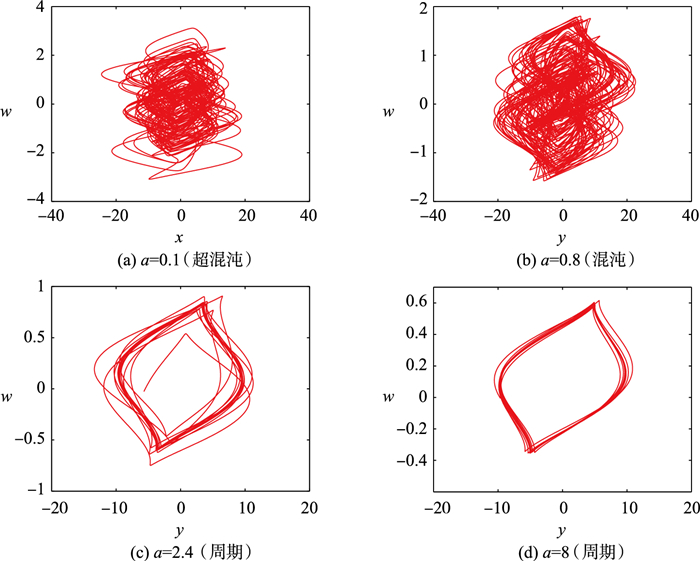
2 分岔分析若未加说明,本文中系统的初始值均为(0.1,0.1,0.1,0.1,0.1)。图 2给出了当b=0.8,a在区间[0, 10]变化时,y的李雅普诺夫指数谱和分岔图,其中ymax为y平面上截取的相轨的最大值范围。当a在区间[0,1.7]的变化时,超混沌轨道、周期轨道和混沌轨道交替出现。当a在区间[1.7,10]中变化时,系统呈周期态。图 3给出了当a=0.1、a=0.8、a=2.4和a=8时系统(3)的相图。
|
| 图 2 b=0.8时系统(3)的李雅普诺夫指数谱和分岔图 Fig.2 Lyapunov exponent spectrum and bifurcation diagram of system (3) with b=0.8 |
|
| 图 3 b=0.8时系统(3)的平面相图 Fig.3 Phase plane diagrams of System (3) with b=0.8 |
用u-n替换系统(3)中的u,系统(3)的拓扑形式不变,只是在第2个方程中添加了一个常数项。
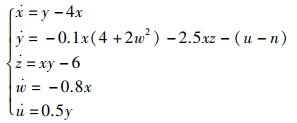
|
(6) |
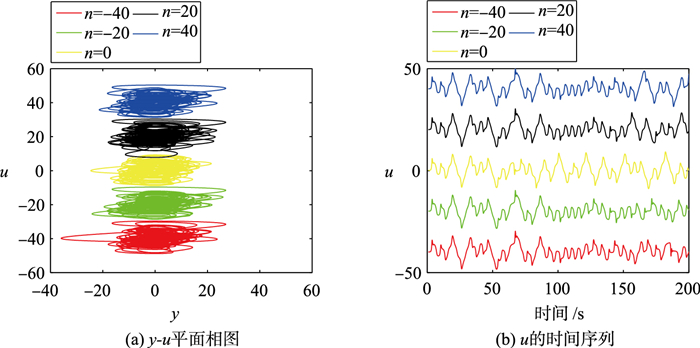
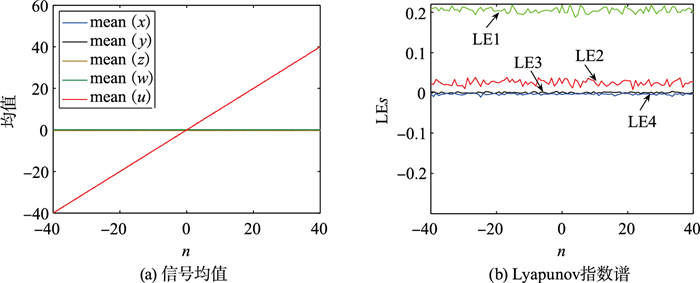
图 4(a)是n取5个不同值时y-u平面相图。图 4(b)是n取5个不同值时的信号波形轨迹。图 5(a)给出了状态变量的信号均值mean函数时的图像,可以直观地看到,随着n的增大,u的信号均值沿直线增加,而其他状态变量信号均值几乎不变。如图 5(b)所示,系统(6)的李雅普诺夫指数谱只有微小的波动,当n从-40变为40时,系统保持超混沌。
|
| 图 4 a=0.1,b=0.8时系统(6)的相图和时间序列 Fig.4 Phase diagrams and time series of system (6) with a=0.1, b=0.8 |
|
| 图 5 a=0.1,b=0.8,初始条件为(0.1,0.1,0.1,0.1,0.1+n)时系统(6)的信号均值和李雅普诺夫指数谱 Fig.5 Mean signal values and Lyapunov exponent spectrum of system (6) with a=0.1, b=0.8 under initial condition (0.1, 0.1, 0.1, 0.1, 0.1+n) |
与一般的偏移增量控制不同,变量z在系统(3) 中仅以乘积因子的形式出现一次。实际上,它还可以通过调节系统忆阻器的参数来实现一维偏移增量控制。做变换z→z-h,有:
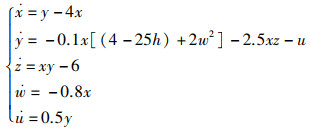
|
(7) |
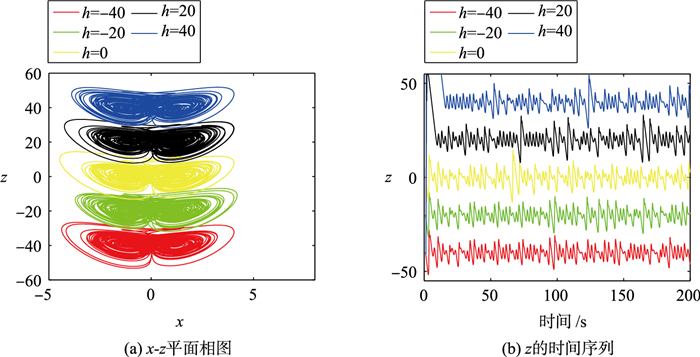
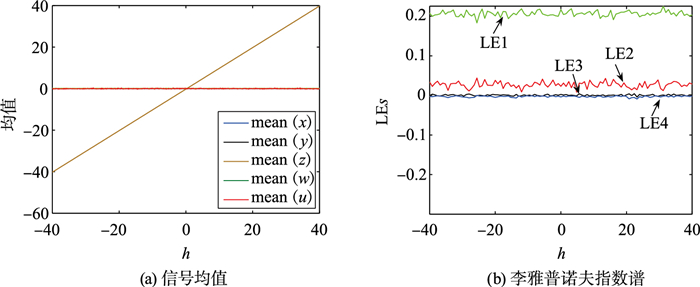
系统(7)第2个方程的磁控忆阻器中的常数4减去25h,就实现了z的偏移增量控制。如图 6(a)所示,当h不断增加时,吸引子沿z轴从小到大移动,相应的偏移时间序列如图 6 (b)所示。在h的变化过程中,状态变量z的信号均值沿直线增加,其他状态变量的信号均值几乎保持不变。图 7(a)演示了这一过程。图 7(b)是系统(7)的李雅普诺夫指数谱,当h从-40变为40时,系统保持超混沌。一些系统具有相对较大的吸引域,初始值不需要根据变量进行修改,这使得偏移控制更容易,但系统(6)和系统(7)的初始值需要根据n和h的值进行更改。
|
| 图 6 a=0.1,b=0.8,初始条件为(0.1,0.1,0.1+h,0.1,0.1)时系统(7) 的相图和时间序列 Fig.6 Phase diagrams and time series of system (7) with a=0.1, b=0.8 under initial conditions (0.1, 0.1, 0.1+h, 0.1, 0.1) |
|
| 图 7 a=0.1,b=0.8,初始条件为(0.1,0.1,0.1+h,0.1,0.1)时系统(7)的信号均值和李雅普诺夫指数谱 Fig.7 Mean signal values and Lyapunov exponent spectrum of system (7) with a=0.1, b=0.8 under initial condition (0.1, 0.1, 0.1+h, 0.1, 0.1) |
为了产生和传输混沌信号,必须首先获得适当的振幅。因此,混沌信号的幅值控制在工程中起着重要的作用。将参数k添加到系统(3)中,得到:
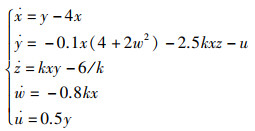
|
(8) |
k≠0时,系统(8)等价于:
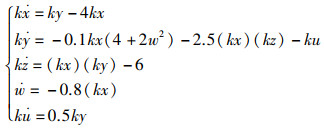
|
(9) |
令kx=x′,ky=y′,kz=z′,ku=u′,得到系统(10):

|
(10) |
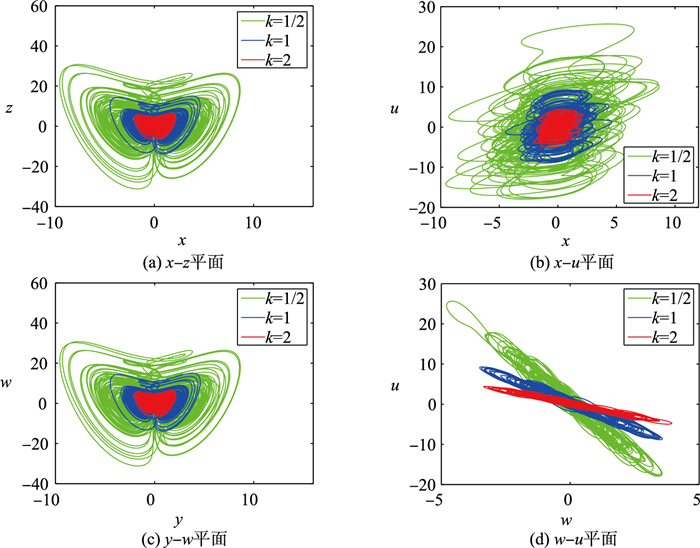
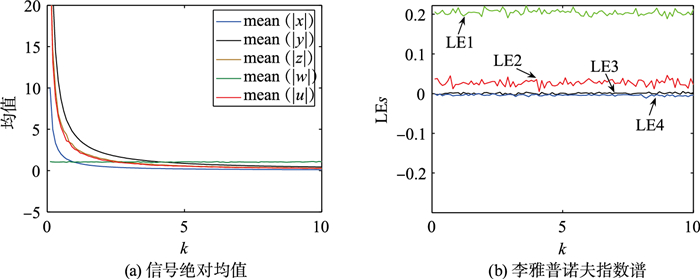
系统(10)和系统(3)具有相同的形式,表明参数k可以调节x、y、z、u的信号幅值,同时系统形式保持不变。图 8给出了k取3个不同的值时,系统(8)在x-z、x-u、y-w和w-u平面的相图。可以观察到,状态变量x、y、z和u的幅值相应地发生改变,而状态变量w的幅值基本保持不变。图 9(a)是当参数k从0到10变化时,系统(8)的超混沌信号的绝对均值。可以观察到,x、y、z和u的绝对均值随着k的变化而变化,w的绝对均值基本保持不变,这与理论分析的结果一致。由图 9(b)可观察到,在调幅过程中,李雅普诺夫指数谱没有太大变化,系统保持超混沌。
|
| 图 8 a=0.1,b=0.8时系统(8)的平面相图 Fig.8 Phase plane diagrams of system (8) with a=0.1, b=0.8 |
|
| 图 9 a=0.1,b=0.8时系统(8)的信号绝对均值和李雅普诺夫指数谱 Fig.9 Mean absolute signal values and Lyapunov exponent spectrum of system (8) with a=0.1, b=0.8 |
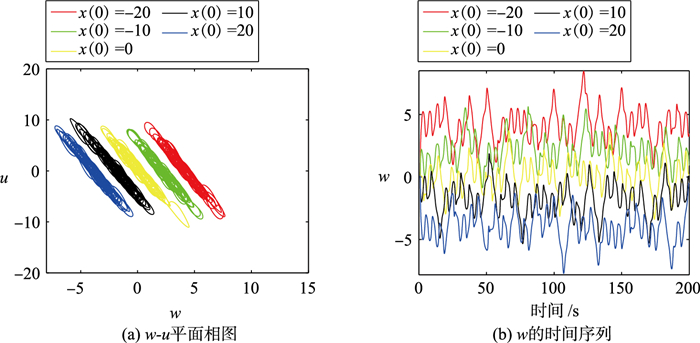
一般来说,当忆阻器作为非线性项引入混沌系统时,它可以进一步提高混沌系统对初始值的敏感性,容易产生基于初始值的偏移现象。目前,超级多稳态是非线性系统的一个重要研究方向,基于忆阻器的初值偏移,值得深入研究。由图 10(a)能观察到,系统(3)在x(0)取不同值时,能够生成多个共存吸引子。图 10(b)进一步证实了这一点。
|
| 图 10 a=0.1,b=0.8,初始条件为(x(0),0.1,0.1,0.1,0.1)时系统(3)的相图和时间序列 Fig.10 Phase diagrams and time series of system (3) with a=0.1, b=0.8 under initial conditions (x(0), 0.1, 0.1, 0.1, 0.1) |
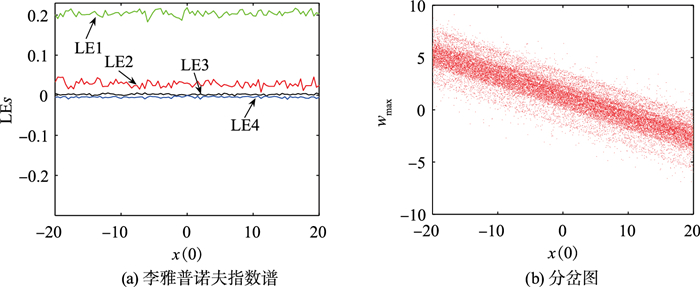
当x(0)取不同的值时,吸引子在w-u平面偏移。图 11给出了当x(0)从-20变为20时系统(3)的李雅普诺夫指数谱和分岔图,它表明,随着x(0)的变化,系统具有无限多个超混沌共存吸引子,这进一步证明了系统(3)具有隐藏超级多稳态。从图 11中可得出结论,初值x(0)的变化改变了吸引子的位置,但对系统的其他动力学行为影响不大。
|
| 图 11 a=0.1,b=0.8,初始条件为(x(0),0.1,0.1,0.1,0.1)时系统(3)的李雅普诺夫指数谱和分岔图 Fig.11 Lyapunov exponent spectrum and bifurcation diagram of system (3) with a=0.1, b=0.8 under initial conditions: (x(0), 0.1, 0.1, 0.1, 0.1) |
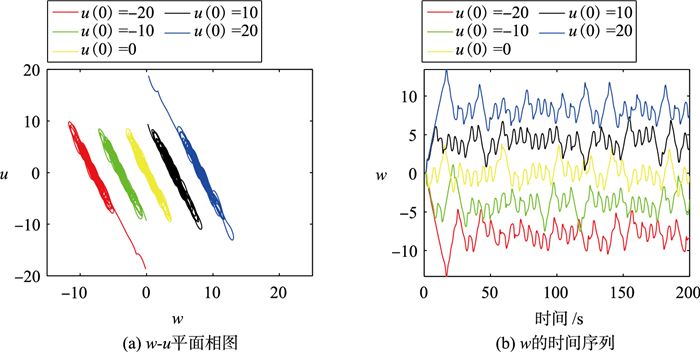
图 12(a)和图 12(b)给出了系统(3)当u(0)取5个不同的值时w-u平面的相图及状态变量的时间序列。从图 12(a)可以看出,系统(3)在u(0)取不同的值时也会生成多个共存吸引子。
|
| 图 12 a=0.1,b=0.8,初始条件为(0.1,0.1,0.1,0.1,u(0))时系统(3)的相图和时间序列 Fig.12 Phase diagrams and time series of system (3) with a=0.1, b=0.8 under initial conditions (0.1, 0.1, 0.1, 0.1, u(0)) |
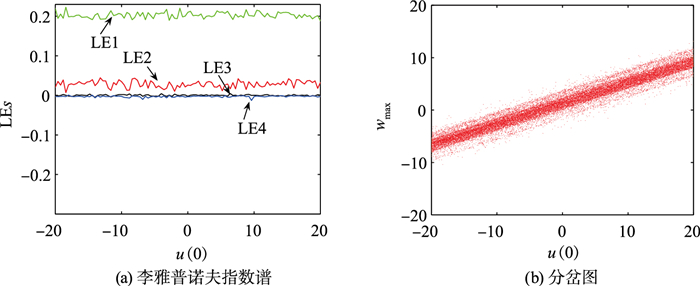
图 13是当u(0)从-20变为20时系统(3)的李雅普诺夫指数谱和分岔图。
|
| 图 13 a=0.1,b=0.8,初始条件为(0.1,0.1,0.1,0.1,u(0))时系统(3)的李雅普诺夫指数谱和分岔图 Fig.13 Lyapunov exponent spectrum and bifurcation diagram of system (3) with a=0.1, b=0.8 under initial condition (0.1, 0.1, 0.1, 0.1, u(0)) |
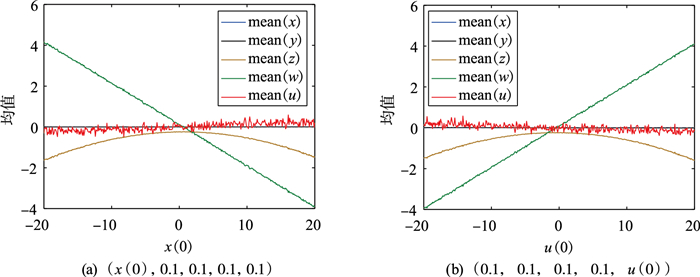
图 14给出了当初始值取(x(0),0.1,0.1,0.1,0.1)和(0.1,0.1,0.1,0.1,u(0))时系统(3)的超混沌信号的均值。比较x(0)和u(0)变化时的超混沌信号均值。当x(0)从-20变为20时,w的信号均值沿直线从大变小。当u(0)从-20变为20时,w的信号均值沿直线从小变大。状态变量x、y和u的振幅均值基本保持不变。
|
| 图 14 a=0.1,b=0.8系统(3)的超混沌信号均值 Fig.14 Mean values of hyperchaotic signals of system (3) with a=0.1, b=0.8 |
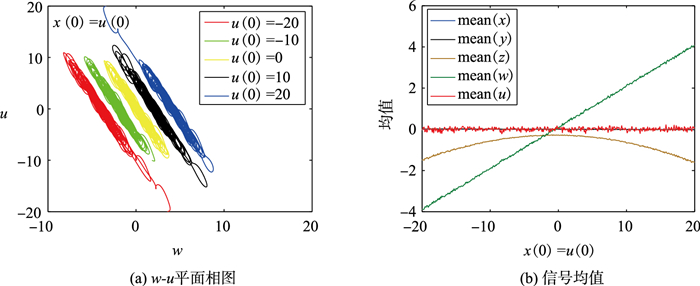
图 15给出了当a=0.1,b=0.8,初始条件为(u(0),0.1,0.1,0.1,u(0))时系统(3)在w-u平面的相图和超混沌信号均值。在w-u平面中的x(0)=u(0)线上选择5个不同的u(0)。这时发现,超混沌吸引子仍然是偏移的,且沿着w轴方向从小到大移动。它表明,在w-u平面的x(0)=u(0)线上,当u(0)从-20变为20时,初始值u(0)对偏移方向的影响更大。
|
| 图 15 a=0.1,b=0.8,初始条件为(u(0),0.1,0.1,0.1,u(0))时系统(3)的相图和信号均值 Fig.15 Phase diagrams and mean signal values of system (3) with a=0.1, b=0.8 under initial condition (u(0), 0.1, 0.1, 0.1, u(0)) |
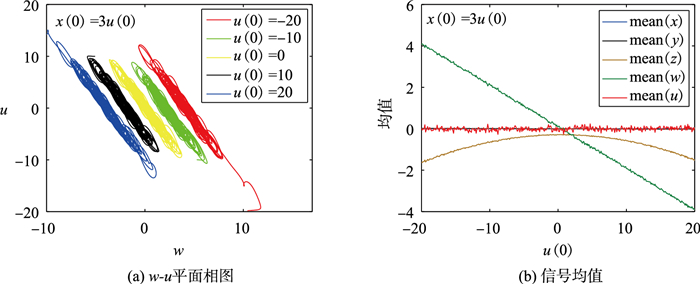
图 16给出了当a=0.1,b=0.8,初始条件为(3u(0),0.1,0.1,0.1,u(0))时系统(3)在w-u平面的相图和超混沌信号均值。取w-u平面中的直线x(0)=3u(0),当u(0)从-20变为20时,选择5个不同的u(0),发现超混沌吸引子沿w轴方向从大到小移动,这意味着初始值x(0)对偏移方向的影响更大。比较两条直线x(0)=u(0)和x(0)=3u(0)上的情况,在直线x(0)=3u(0)上x(0)的变化范围是直线x(0)=u(0)上的三倍,但每个状态变量的信号均值的范围基本保持不变,仅在相对w轴的偏移方向上有所不同。
|
| 图 16 a=0.1,b=0.8,初始条件为(3u(0),0.1,0.1,0.1,u(0))时系统(3)的相图和信号均值 Fig.16 Phase diagrams and mean signal values of system (3) with a = 0.1, b=0.8 under initial condition (3u(0), 0.1, 0.1, 0.1, u(0)) |
系统(3)的模拟电路方程为
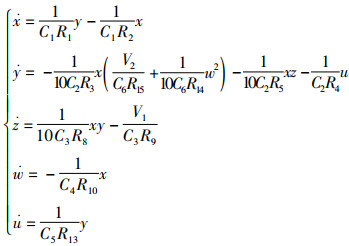
|
(11) |
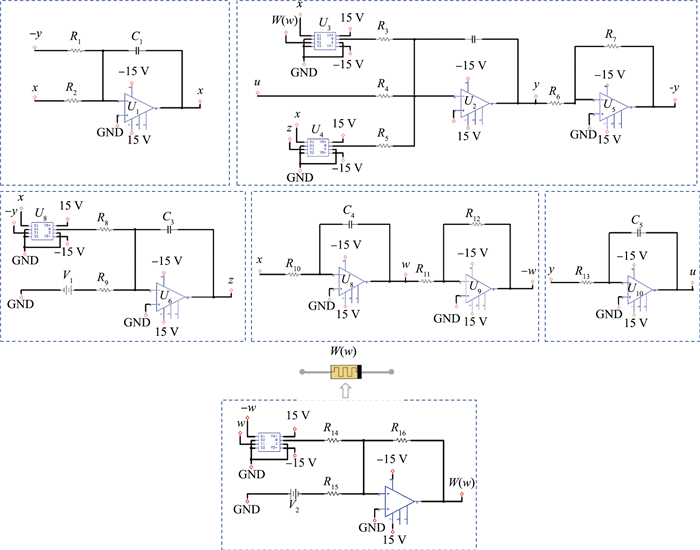
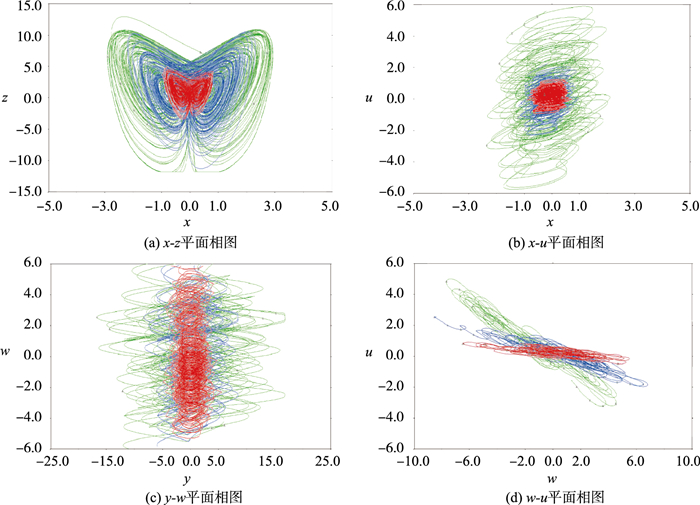
电阻R1,R3,R4,R6,R7,R9,R11,R12,R15,R16的值均取100 kΩ,R2=25 kΩ,R5=4 kΩ,R8=10 kΩ,R10=125 kΩ,R13=200 kΩ,R14=5 kΩ,C1,C2,C3,C4,C5,C6的值均取0.1 V,V1=6 V,V2=4 V。同时采用LM741CN运算放大器和AD633JN乘法器构建模拟电路。图 17给出了系统(11)的电路图,图 18是示波器中显示的超混沌吸引子,其相图与计算机模拟的相图高度相似。当R5=4 kΩ,R8=10 kΩ,R10=125 kΩ,V1=6 V时,超混沌系统的相图是图 19中的绿色吸引子。R5,R8,R10,V1的值同时除以2,超混沌系统的相图是图 19中蓝色吸引子,R5,R8,R10,V1的值同时除以4,超混沌系统相图是图 19中是红色吸引子。
|
| 图 17 系统(11)的电路图 Fig.17 The circuit schematic of system (11) |
|
| 图 18 系统(11)示波器中的平面相图 Fig.18 Phase plane diagrams of system (11) shown in the oscilloscope |
|
| 图 19 当R5,R8,R10,V1取不同值时系统(11)在示波器中的平面相图 Fig.19 Phase plane diagrams of system (11) shown in the oscilloscope when R5, R8, R10, V1 are taken different values |
本文对一个5维超混沌系统进行了动力学分析。该系统具有高维数、相对较少项数、无平衡等特点,同时系统还具有分岔参数、幅值控制参数。该系统在初值x(0)和u(0)发生变化时,吸引子会产生偏移,同时在x-u平面的不同的直线上,偏移方向会发生变化,且存在一些特殊的现象,如当一些初始值的变化范围相差很大时,状态变量的信号均值的范围可以基本保持不变。最后,基于系统状态方程和基尔霍夫定律,设计了忆阻混沌电路。在示波器上显示了相图和调幅后的相图,这证明了所提出系统的物理可实现性。当存在多种共存状态时,系统具有多种正常运行模式,会对工作环境的变化表现出较强的适应性。因此,利用忆阻器构建多共存吸引子混沌系统的研究仍有很大的发展空间和研究价值。接下来,将继续研究初始值沿平面或空间中的曲线偏移时吸引子的变化情况。
| [1] |
LI C B, SPROTT J C. Amplitude control approach for chaotic signals[J]. Nonlinear Dynamics, 2013, 73: 1335-1341. DOI:10.1007/s11071-013-0866-z |
| [2] |
ZHANG X, LI C B, DONG E Z. A conservative memristive system with amplitude control and offset boosting[J/OL]. International Journal of Bifurcation and Chaos, 2022, 32(4)[2023-01-12]. https://www.worldscientific.com/doi/abs/10.1142/S0218127422500572.
|
| [3] |
ZHANG H Y, GU Z Y, LEI T F. Coexisting chaotic attractors in a memristive system and their amplitude control[J]. Pramana-Journal of Physics, 2020, 94(62): 1-9. |
| [4] |
HU W, AKGUL A, LI C B. A switchable chaotic oscillator with two amplitude-frequency controllers[J/OL]. Journal of Circuits, Systems, and Computers, 2017, 26(10)[2022-11-19]. https://www.worldscientific.com/doi/abs/S0218126617501584. DOI: 10.1142/s0218126617501584.
|
| [5] |
LU T, LI C B, WANG X. A memristive chaotic system with offset-boostable conditional symmetry[J]. The European Physical Journal Special Topics, 2020, 229: 105-1069. |
| [6] |
LI C B, SPROTT J C, ZHANG X. Constructing conditional symmetry in symmetric chaotic systems[J]. Chaos, Solitons and Fractals, 2022, 155[2022-10-05]. https://www.sciencedirect.com/science/article/pii/S0960077921010778. DOI: 10.1016/j.chaos.2021.111723.
|
| [7] |
LI C B, SPROTT J C, LIU Z. Multistability in the Lorenz System: A broken butterfly[J]. International Journal of Bifurcation and Chaos, 2014, 24(10)[2022-11-05]. http://www.worldscientific.com/doi/abs/10.1142/S021812744501314.
|
| [8] |
LI C L, LI H M, LI W. Dynamics, implementation and stability of a chaotic system with coexistence of hyperbolic and non-hyperbolic equilibria[J]. International Journal of Electronics, 2018, 84: 199-205. |
| [9] |
PHAM V T, VOLOS C, VAIDYANATHAN S. A chaotic system with an infinite number of equilibrium points: dynamics, horseshoe, and synchronization[J/OL]. Advances in Mathematical Physics, 2016[2022-10-12]. https://www.hindawi.com/journals/amp/2016/4024836. DOI: 10.1155/2016/4024836.
|
| [10] |
XIA X Z, ZENG Y H, LI Z J. Coexisting multiscroll hyperchaotic attractors generated from a novel memristive jerk system[J]. Pramana-Journal of Physics, 2018, 91: 82. DOI:10.1007/s12043-018-1657-3 |
| [11] |
HUYNH V V, KHALAF A J M, ALSAEDI A. A new memristive chaotic flow with a line of equilibria[J]. The European Physical Journal Special Topics, 2019, 228: 2339-2349. DOI:10.1140/epjst/e2019-900055-9 |
| [12] |
BAO B C, XU Q, BAO H, et al. Extreme multistability in a memristive circuit[J]. Electronics Letters, 2016, 52: 1008-1010. DOI:10.1049/el.2016.0563 |
| [13] |
XU B R, WANG G Y, WANG X Y. A third-order memristive Wien-bridge circuit and its integrable deformation[J]. Pramana-Journal of Physics, 2019(93): 42. |
| [14] |
TOUR J M, HE T. Electronics: the fourth element[J]. Nature, 2008, 453: 42-43. DOI:10.1038/453042a |
| [15] |
BAO B C, ZOU X, LIU Z. Generalized memory element and chaotic memory system[J]. International Journal of Bifurcation and Chaos, 2013, 23(8)[2022-09-10]. https://www.worldscientific.com/doi/abs/10.1142/S0218127413501356.
|
| [16] |
Singh J P, Roy B K. Five new 4-D autonomous conservative chaotic systems with various type of non-hyperbolic and lines of equilibria[J]. Chaos, Solitons and Fractals, 2018, 114: 81-91. DOI:10.1016/j.chaos.2018.07.001 |
| [17] |
LI Q D, HU S Y, ZENG G. Hyperchaos and horseshoe in a 4D memristive system with a line of equilibria and its implementation[J]. International Journal of Circuit Theory and Applications, 2014, 42: 1172-1188. DOI:10.1002/cta.1912 |
| [18] |
WANG M J, DENG Y, LIAO X H. Dynamics and circuit implementation of a four-wing memristive chaotic system with attractor rotation[J]. International Journal of Non-Linear Mechanics, 2019, 111: 149-159. DOI:10.1016/j.ijnonlinmec.2019.02.009 |
| [19] |
MEZATIOA B A, MOTCHONGOM M T, TEKAM B R W. A novel memristive 6D hyperchaotic autonomous system with hidden extreme multistability[J]. Chaos, Solitons and Fractals, 2019, 120: 100-115. DOI:10.1016/j.chaos.2019.01.015 |
| [20] |
WU H G, YE Y, BAO B C. Memristor initial boosting behaviors in a two-memristor-based hyperchaotic system[J]. Chaos, Solitons and Fractals, 2019, 121: 178-185. DOI:10.1016/j.chaos.2019.03.005 |
| [21] |
秦铭宏, 赖强, 吴永红. 具有无穷共存吸引子的简单忆阻混沌系统的分析与实现[J]. 物理学报, 2022, 71(16): 160502-1-160502-11. QIN M H, HAI Q, WU Y H. Analysis and implementation of simple four-dimensional memristive chaotic system with infinite coexisting attractors[J]. Acta Physica Sinica, 2022, 71(6): 160502-1-160502-11. |
| [22] |
李晓霞, 郑驰, 王雪, 等. 一个新的具有超级多稳态的五维忆阻超混沌系统[J]. 哈尔滨工业大学学报, 2022, 54(3): 163-170. LI X X, ZHENG C, WANG X, et al. A novel five-dimensional memristive hyperchaotic system with extreme multistability[J]. Journal of Harbin Institute of Technology, 2022, 54(3): 163-170. |
| [23] |
DU C H, LIU L C, ZHANG Z P. A memristive conservative chaotic circuit with two different offset boosting behaviors[J/OL]. International Journal of Electronics and Communications, 2022, 147[2022-11-12]. https://www.sciencedirest.com/science/article/abs/pii/S1007570420303993. DOI: 10.1016/j.cnsns.2020.105569.
|
| [24] |
YAN S H, REN Y, SONG Z L. A memristive chaotic system with rich dynamical behavior and circuit implementation[J]. Integration, 2022, 85: 63-75. DOI:10.1016/j.vlsi.2022.03.003 |



