2. 蚌埠学院理学系, 安徽 蚌埠 233030;
3. 沈阳工业大学理学院, 辽宁 沈阳 110001
2. Department of Science, Bengbu College, Bengbu 233030, China;
3. College of Science, Shenyang University of Industry, Shenyang 110001, China
1 引言
生存理论是由法国数学家Aubin于1990年提出的系统理论[1],因其具有广泛的应用背景,现已被主要应用于生物、 经济和社会等系统的研究中. 目前,国内外已有部分学者致力于控制系统生存性的研究,并取得了一系列的研究成果[2, 3, 4, 5, 6]. 生存性还可被应用于解决控制系统中的其它问题,诸如,可达性问题[7]、 稳定性问题[8, 9, 10, 11]、 微分对策问题[12]等.
对控制系统的生存性研究主要分为两个方面: 一是判断系统在一个区域上是否生存,是否存在合适的控制使得系统在指定区域上生存,以及如何进行生存控制器设计[5, 13, 14, 15]; 二是对给定的系统,去寻找它的生存域,或者计算系统的最大生存域[16, 17, 18, 19]. 系统生存域指的是初始状态始于这个区域内的系统轨迹始终不离开此区域.
本文研究了一般的非线性系统的生存性问题. 首先利用生存理论给出了非线性系统在不等式表示区域上生存的充要条件. 然后,基于较为成熟的李亚普诺夫稳定性理论和无源性理论,分析了非线性系统的生存性,并得到了系统的生存域. 最后,仿真验证了本文结论的正确性. 本文从新的角度,为系统的生存性研究打开了一个新的思路.
2 预备知识考虑一般形式的微分包含
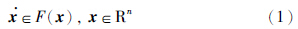
 =f(x),当F(x)={f(x,u)u∈U}时,微分包含(1)即为非线性系统
=f(x),当F(x)={f(x,u)u∈U}时,微分包含(1)即为非线性系统 =f(x,u).
=f(x,u). 定义1[1] 设K⊂Rn,如果对任意初始状态x0∈K,存在解x(t),使得∀t≥0,x(t)∈K,则称微分包含(1)在集合K上是生存的,解x(t)也称为生存解. 此时集合K称为系统的生存域.
定义2[1] 设K⊂Rn非空,集合K在x∈K处的切锥定义为
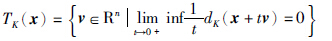
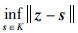 .
. 考虑闭集K={x∈Rn|φ(x)≤0},其中φ(x)为Rn上的连续可微函数,下面给出集合K在x点的约束品性.
约束品性1[1] 存在w0∈Rn,使得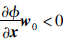 .
.
约束品性2[20] clγ(x)=Γ(x)成立,其中cl为闭包,
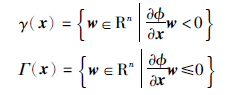
命题1[1, 20] 如果集合K在x点满足约束品性1和约束品性2,则有TK(x)=Γ(x).
引理1[1] 微分包含(1)在闭集K⊂Rn上生存的充要条件为
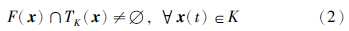
对于集合K内部的任意一点x总有TK(x)=Rn,这时(2)式总成立,于是要判别(2)式是否成立,只需考虑集合K的边界点.
下面考虑系统 =f(x)和
=f(x)和 =f(x,u)的生存性问题,在给出主要结果前,先提出以下假设.
=f(x,u)的生存性问题,在给出主要结果前,先提出以下假设.
假设 f(x)为关于x的利普希茨函数,f(x,u)为关于x和u的利普希茨函数,其中x∈Rn,u∈Rm.
3 主要结果
定理1 设集合K满足约束品性1和约束品性2,则系统 =f(x)在集合K上生存当且仅当
=f(x)在集合K上生存当且仅当
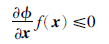
 =f(x,u)在集合K上生存当且仅当
=f(x,u)在集合K上生存当且仅当
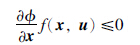
证明 由命题1,TK(x)=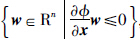 ,再由引理1,微分包含
,再由引理1,微分包含 ∈F(x)在集合K上生存的充要条件为
∈F(x)在集合K上生存的充要条件为
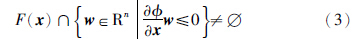
 =f(x),(3)式为
=f(x),(3)式为
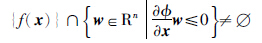
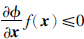 .
.
对于系统 =f(x,u),(3)式为
=f(x,u),(3)式为
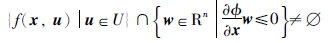
 . 定理得证.
. 定理得证.
定理2 设x=0为系统 =f(x)的平衡点,v(x)为连续可微函数,且v(0)=0,∀x≠0,v(x)>0,则系统在x=0处稳定当且仅当系统在集合K={x∈Rn|v(x)≤c}(c为任意固定的常数)上生存.
=f(x)的平衡点,v(x)为连续可微函数,且v(0)=0,∀x≠0,v(x)>0,则系统在x=0处稳定当且仅当系统在集合K={x∈Rn|v(x)≤c}(c为任意固定的常数)上生存.
证明 令φ(x)=v(x)-c,则集合

 =f(x)在集合K上生存当且仅当
=f(x)在集合K上生存当且仅当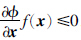 ,即
,即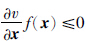 ,从而有
,从而有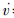 ≤0,
≤0,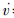 半负定,于是系统
半负定,于是系统 =f(x)在x=0处稳定.
=f(x)在x=0处稳定.
注1 该定理表明,系统 =f(x)在平衡点的李亚普诺夫稳定性等价于系统在其任意李亚普诺夫函数水平集上的生存性,任意的李亚普诺夫函数水平集都是系统的生存域.
=f(x)在平衡点的李亚普诺夫稳定性等价于系统在其任意李亚普诺夫函数水平集上的生存性,任意的李亚普诺夫函数水平集都是系统的生存域.
定理3 如果系统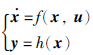 对于一个连续可微的半正定存储函数v(x)是无源的,且对所有的y≠0,存在局部利普希茨函数g(y)满足yTg(y)≥0,则可通过输出反馈u=-g(y)使得系统
对于一个连续可微的半正定存储函数v(x)是无源的,且对所有的y≠0,存在局部利普希茨函数g(y)满足yTg(y)≥0,则可通过输出反馈u=-g(y)使得系统 =f(x,u)在集合K={x∈Rn|v(x)≤c}(c为任意固定的常数)上生存,其中h(x)为x的连续函数.
=f(x,u)在集合K={x∈Rn|v(x)≤c}(c为任意固定的常数)上生存,其中h(x)为x的连续函数.
证明 令φ(x)=v(x)-c,则
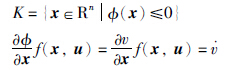
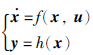 的无源性知
的无源性知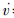 ≤yTu,于是
≤yTu,于是
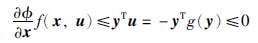
注2 该定理说明,在一定条件下,由系统的无源性,可以通过适当地反馈控制使得系统在区域K={x∈Rn|v(x)≤c}上生存,而且由存储函数确定的集合K即为系统的一个生存域.
4 仿真算例算例1 考虑系统1
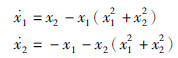
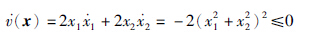
 |
| 图 1 系统1的相平面曲线Fig. 1 Phase-plane curve of the system 1 |
算例2 考虑系统2
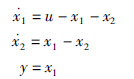
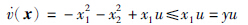
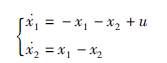
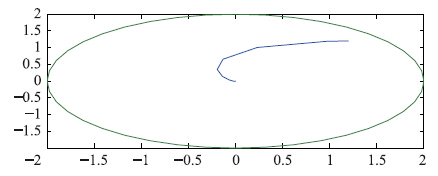 |
| 图 2 系统2的相平面曲线Fig. 2 Phase-plane curve of the system 2 |
本文利用较为成熟的稳定性和无源性理论,对系统的生存性进行了初步研究,证明了非线性系统的稳定性等价于系统在其任意李亚普诺夫函数水平集上的生存性,系统的任意李亚普诺夫函数水平集均为系统的生存域. 然后证明了,在一定条件下,通过适当的反馈控制可以使得系统在存储函数确定的区域上生存. 最后,仿真算例验证了本文结论的正确性. 另外,定理2和定理3中得到的生存域其实也是系统的安全域,因此,在系统安全域设计方面,本文结论也具有一定的参考意义.
| [1] | Aubin J P. Viability theory[M]. Boston,USA: Birkhauser,1991. |
| [2] | Aubin J P,Lygeros J,Quincampoix M,et al. Impulse differential inclusions: A viability approach to hybrid systems[J]. IEEE Transactions on Automatic Control,2002,47(1): 2-20. |
| [3] | Labinaz G,Guay M. Robust viability of hybrid systems[J]. Nonlinear Analysis: Hybrid Systems,2008(2): 184-195. |
| [4] | Panagou D,Kyriakopoulos K J. Viability control for a class of underactuated systems[J]. Automatica,2013,49(1): 17-29. |
| [5] | Gao Y. Viability criteria for differential inclusions[J]. Journal of Systems Science and Complexity,2011,24(5): 825-834. |
| [6] | 高岩,陈征. 混杂系统的演化和生存[J]. 上海理工大学学报,2011,33(6): 669-678. Gao Y,Chen Z. The viability and evolution of hybrid systems[J]. Journal of University of Shanghai for Science and Technology,2011,33(6): 669-678. |
| [7] | Gao Y,Lygeros J,Quincampoix M. On the reachability problem of uncertain hybrid systems[J]. IEEE Transactions on Automatic Control,2007,52(9): 1572-1586. |
| [8] | Gao Y,Lygeros J,Quincampoix M,et al. On the control of uncertain impulsive system: Approximate stabilisation and controlled invariance[J]. International Journal of Control,2004,77(16): 1393-1407. |
| [9] | Quincampoix M,Seube N. Stabilization of uncertain control systems through piecewise constant feedback[J]. Journal of Mathematical Analysis and Applications,1998,218(1): 240-255. |
| [10] | Gao Y,Lygeros J,Quincampoix M,et al. Approximate stabilisation of uncertain hybrid systems[M] //Lecture Notes in Computer Science,vol 2623. Berlin,Germany: Springer-Verlag,2003: 203-215. |
| [11] | Lou Z E,Gao Y. The exponential stability for a class of hybrid systems[J].Asian Journal of Control,2013,15(4): 1-6. |
| [12] | Cardaliaguet P,Quincampoix M,Saint-Pierre P. Pursuit differential games with state constraints[J]. SIAM Journal of Control and Optimization,2002,39(5): 1615-1632. |
| [13] | 高岩. 一类非线性控制系统可生存性的判别[J]. 信息与控制,2005,34(4): 510-512. Gao Y. Determining the viability for a class of nonlinear control systems[J]. Information and Control,2005,34(4): 510-512. |
| [14] | 高岩. 一类非线性控制系统关于非光滑区域生存性的判别[J]. 控制与决策,2006,21(8): 923-925.Gao Y. Determining the viability for a class of nonlinear control systems on a region with nonsmooth boundary[J]. Control and Decision,2006,21(8): 923-925. |
| [15] | 高岩,娄志娥. 一类混杂系统的生存控制设计[J]. 控制与决策,2009,24(2): 254-258. Gao Y,Lou Z E. Viable control design for a class of hybrid systems[J]. Control and Decision,2009,24(2): 254-258. |
| [16] | Broucke M E,Turriff J. Viabiltiy kernels for nonlinear control systems using bang controls[J].IEEE Transactions on Automatic Control,2010,55(5): 1280-1284. |
| [17] | 高岩. 线性控制系统的生存域[J]. 控制与决策,2007,22(7): 833-835. Gao Y. On viable set for a linear control system[J]. Control and Decision,2007,22(7): 833-835. |
| [18] | 陈征,高岩. 一维混杂控制系统可生存域计算[J]. 上海理工大学学报,2007,29(3): 220-222. Chen Z,Gao Y. Computation of viability for one-dimensional hybrid control systems[J]. Journal of University of Shanghai for Science and Technology,2007,29(3): 220-222. |
| [19] | 陈征,高岩. 一维控制系统的最大生存域及人口模型[J]. 控制工程,2013,20(3): 540-543,552. Chen Z,Gao Y. The maximal viability for one-dimensional control systems and the population model[J]. Control Engineering of China,2013,20(3): 540-543,552. |
| [20] | Demyanov V F,Rubinov A M. Constructive nonsmooth analysis[M]. Frankfurt,Germany: Peter Lang,1995. |



