2. 中南大学物理与电子学院, 湖南 长沙 410083
2. School of Physics and Electronics, Central South University, Changsha 410083, China
1 引言
自1990年Pecora和Carroll[1]首次提出基于驱动—响应方法的混沌同步以来,混沌系统的同步控制引起了人们的广泛关注,并提出了不同的混沌同步方案,如完全同步[2]、相同步[3]和追踪同步[4]等. 其中追踪同步通过施加控制使受控系统的输出信号达到任意给定的参考轨道,是当前混沌系统控制的研究热点[5, 6, 7, 8, 9],如文[7]中通过设计单一控制器,将Rssler系统单一变量控制到任意轨道; 文[8]设计了一组控制器,可以控制Dynamos系统到任意轨道或期望的平衡点; 文[9]设计了非线性控制器,控制Chen系统x变量到任意参考信号. 然而这些文献中报道的追踪控制器设计比较复杂,在实际应用中并不是很方便,另外文[7]中的控制器含有追踪信号的二阶导数,且要求追踪信号二阶可微,所以有必要设计相对简单的控制器,以实现连续混沌系统的追踪同步. 文[10]对洛伦兹系统进行简化,得到单参数简化洛伦兹系统,并表明该系统具有丰富动力学特性. 近年来,人们研究了简化洛伦兹系统的模拟电路实现[11]、现场可编程门阵列(field programmable gate array,FPGA)数字电路实现[12]、投影同步[13]和Active同步控制[14]等. 混沌同步算法研究为当前混沌研究领域的热点[15, 16, 17],且混沌系统追踪同步控制技术在混沌保密通讯及混沌加密领域中具有广泛的应用前景[18],所以开展简化洛伦兹系统的追踪同步控制研究具有重要的理论和实际意义.
本文以简化洛伦兹系统为研究对象,基于李亚普诺夫稳定性原理,设计控制简化洛伦兹系统单变量到任意轨道的控制器,实现简化洛伦兹系统追踪同步控制,并分析追踪同步系统的性能. 从理论推导与数值仿真两方面证明该方法的有效性. 最后总结全文并指出下一步研究方向.
2 追踪同步原理及控制器设计对洛伦兹系统进行简化,得到单参数混沌系统,即简化洛伦兹混沌系统[10]
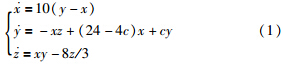
(1) 当系统参数c∈[-1. 59,7. 75]时,系统(1)大部分处于混沌状态;
(2) 当c=-1时,系统(1) 是经典的洛伦兹系统;
(3) 当c=0时,系统(1)第2个方程中不含y项;
(4) 当c=6时,系统(1)第2个方程中不含x项;
(5) 参数c在范围[-1. 59,7. 75]内变化时,系统呈现丰富的分岔行为;
(6) 根据文[10]可知,系统(1)具有3种不同拓扑结构[19]的吸引子. 可见研究简化洛伦兹系统的追踪控制同步具有代表意义. 当c=3.4时,系统(1)的吸引子如图 1所示.
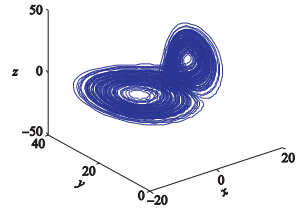 |
| 图 1 c=3.4时简化洛伦兹系统吸引子Fig. 1 Attractor of the simplified Lorenz system when c=3.4 |
本文通过设计一个控制器 U =[u1,u2,u3],使得受控简化洛伦兹系统的输出信号x(t)追踪给定的参考信号r(t),即要求误差信号e1(t)=x(t)-r(t)满足

参考信号r(t)为可微信号,即信号的导数是存在的,当然待追踪信号应当是有界的. 在实际加密应用中,追踪的信号一般为连续混沌信号,此类信号是连续可微的,另外,三角函数信号和直流信号也满足要求. 受控系统方程为
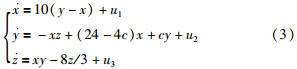
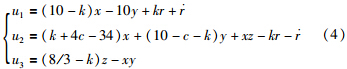
下面从理论上对设计的控制器进行证明.
定理1 当控制器(4)中控制参数k>0时,x(t)可以实现追踪目标r(t),且按指数率收敛到参考信号r(t).
证明 设
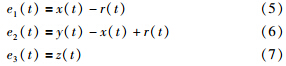
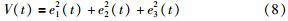
将式(5)~式(7)代入式(8),则有
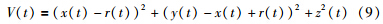
结合设计的控制器(4)和受控系统(2),则李亚普诺夫函数V(t)的导数为
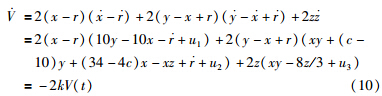
因为V(t)≥0,若k>0,则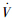 (t)≤0.根据李亚普诺夫稳定性定理可知,采用本文设计的控制器,随着t→∞,同步系统误差函数将收敛到0.接下来证明受控系统(2)的输出信号x(t)是以指数速率收敛到参考信号r(t).
(t)≤0.根据李亚普诺夫稳定性定理可知,采用本文设计的控制器,随着t→∞,同步系统误差函数将收敛到0.接下来证明受控系统(2)的输出信号x(t)是以指数速率收敛到参考信号r(t).
根据式(10)和微积分知识可得
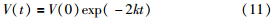

因此,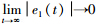 ,可见受控系统(2)的输出信号x(t)按指数速率收敛到任意给出的参考信号r(t).
,可见受控系统(2)的输出信号x(t)按指数速率收敛到任意给出的参考信号r(t).
这里,采用受控系统(2)分别追踪直流信号、正弦信号和超混沌信号,验证同步控制器(4)的有效性. 同时改变控制参数k的值,并分析追踪控制器随控制参数变化时的同步性能. 不做特殊说明,数值仿真时,取k=2,系统(2)初始条件设为x0=0.4,y0=0.2,z0=0.3,参数c=1,时间步长为0.01 s. 利用四阶Runge-Kutta法求解方程(2),并在t=15 s时开启控制器.
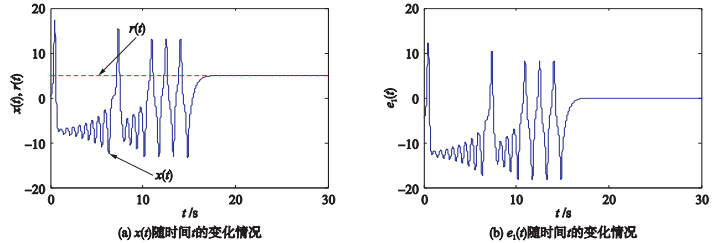
3.1 追踪直流信号选取参考信号为直流信号r(t)=5,根据定理1,设计相应的同步控制器为
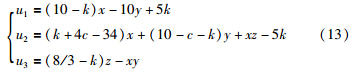
得到的简化洛伦兹系统追踪直流信号r(t)=5的效果如图 2(a)所示,误差如图 2(b)所示. 可见在开启控制器约3 s后,简化洛伦兹系统已追踪上直流信号r(t)=5. 由图 2(b)也可以看出,当t接近18 s时,误差曲线已经基本稳定在0附近.
 |
| 图 2 简化洛伦兹系统追踪直流信号的仿真结果Fig. 2 Simulation results of the simplified Lorenz system to track the DC (direct current) signal |
选取参考信号为正弦信号r(t)=10sin(2t),根据式(4),控制器设计为
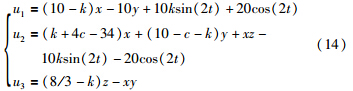
简化洛伦兹系统追踪正弦信号r(t)=10sin(2t)的效果如图 3(a)所示,误差如图 3(b)所示. 可见系统(2)在开启控制器约3 s后追踪到正弦信号r(t)=10sin(2t),其误差曲线此时也稳定在0附近.
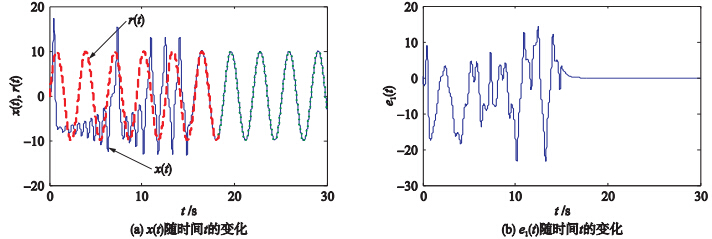 |
| 图 3 简化洛伦兹系统追踪正弦信号的仿真结果Fig. 3 Simulation results of the simplified Lorenz system to track the sinusoidal signal |
简化洛伦兹超混沌系统方程为[20]
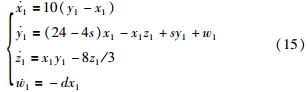
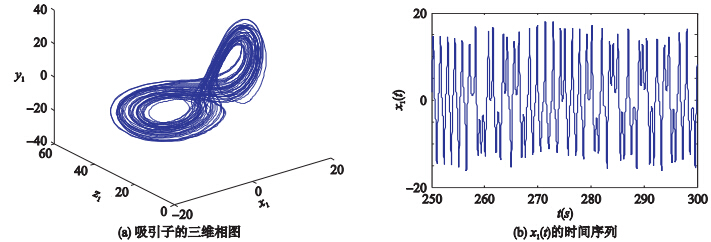 |
| 图 4 简化超混沌洛伦兹系统Fig. 4 Simplified hyperchaotic Lorenz system |
选取参考信号为x1序列,根据式(4),设计控制器为
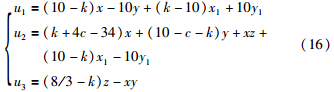
仿真过程中,简化超混沌洛伦兹系统初值为x0=1,y0=2,z0=3,w0=4,参数s=-1,d=5,得到简化洛伦兹系统追踪超混沌信号的效果如图 5所示. 可见,在开启控制器后,简化洛伦兹系统x序列很快就追踪同步到简化超混沌系统的x1序列轨道上,实现简化Lorenz系统追踪混沌信号目标.
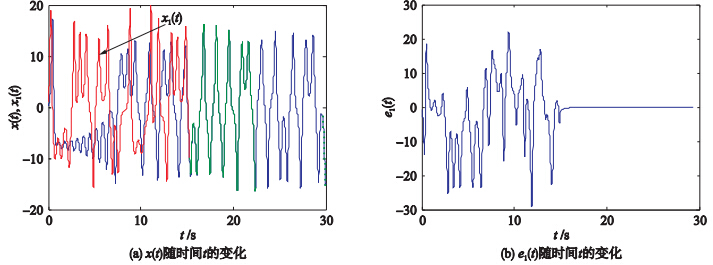 |
| 图 5 简化洛伦兹系统追踪超混沌信号的仿真结果Fig. 5 Simulation results of the simplified Lorenz system to track the hyperchaotic signal |
分析控制参数k取不同值时,达到追踪同步时间的变化情况. 由式(10)可知,对于任意给定的参考信号,误差系统的收敛特性都是一样的,本文以追踪正弦曲线为例,研究追踪同步时间随k的变化情况. 这里,追踪控制器在t=0 s时就开启. 当k分别取1、2、5和10时,误差如图 6所示,对应的线条分别标记为①、②、③和④,可见随着k值的增加,追踪同步建立时间越短,即在实际应用时应选取稍大的控制参数k以获取更好的追踪性能,但从③和④可知,当k增加到一定程度后,对同步性能的改善效果就不明显了.
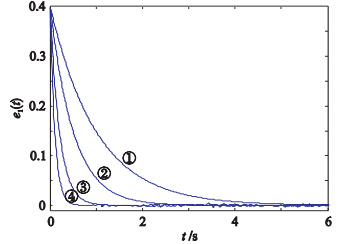 |
| 图 6 控制参数k取不同值时收敛时间变化图Fig. 6 Convergence time variation results with different control parameter k |
本文设计了简化洛伦兹系统的追踪同步控制算法,从理论证明(基于李亚普诺夫指数谱稳定性原理)和仿真实验(追踪直流信号、正弦曲线和超混沌信号)两方面验证设计的控制器的有效性,并得出以下结论:
(1) 本文设计的控制器相对于其它文献中的控制器更为简单,有利于混沌系统的实际应用.
(2) 简化洛伦兹系统为单参数连续混沌系统,具有代表性. 因此,该追踪控制器设计方法可以应用于其它混沌系统.
(3) 同步性能分析结果表明,同步性能与控制参数k有关,采用相对大的控制参数可以显著缩短同步时间.
下一步工作将采用本文提供的追踪同步方案进行混沌保密通信的应用研究.
| [1] | Pecora L M, Carroll T L. Synchronization in chaotic systems[J]. Physical Review Letters, 1990, 64(8): 821-824. |
| [2] | Mahmoud E E. Complex complete synchronization of two nonidentical hyperchaotic complex nonlinear systems[J]. Mathematical Methods in the Applied Sciences, 2014, 37(3): 321-328. |
| [3] | Matheny M H, Grau M, Villanueva L G, et al. Phase synchronization of two anharmonic nanomechanical oscillators[J]. Physical Review Letters, 2014, 112(1): 014101. |
| [4] | Njah A N. Tracking control and synchronization of the new hyperchaotic Liu system via backstepping techniques[J]. Nonlinear Dynamics, 2010, 61(1/2): 1-9. |
| [5] | Lü L, Luan L, Meng L, et al. Study on spatiotemporal chaos tracking synchronization of a class of complex network[J]. Nonlinear Dynamics, 2012, 70(1): 89-95. |
| [6] | Li C L. Tracking control and generalized projective synchronization of a class of hyperchaotic system with unknown parameter and disturbance[J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 17(1): 405-413. |
| [7] | 陈士华, 谢进, 陆君安, 等. Rössler混沌系统的追踪控制与同步[J]. 物理学报, 2002, 51(4): 749-752. Chen S H, Xie J, Lu J A, et al. Tracking control and synchronization of the Rössler's chaotic system[J]. Acta Physica Sinica, 2002, 51(4): 749-752. |
| [8] | 闵富红, 王执铨. 复杂Dynamos混沌系统的追踪控制与同步[J]. 物理学报, 2008, 57(1): 31-36. Min F H, Wang Z Q. Generalized projective synchronization and tracking control of complex Dynamos chaotic systems[J]. Acta Physica Sinica, 2008, 57(1): 31-36. |
| [9] | 谌龙, 王德石. 陈氏混沌系统的稳定追踪控制[J]. 控制与决策, 2007, 22(8): 935-938. Chen L, Wang D S. Stable tracking control of Chen's chaotic system[J]. Control and Decision, 2007, 22(8): 935-938. |
| [10] | Sun K H, Sprott J C. Dynamics of a simplified Lorenz system[J]. International Journal of Bifurcation and Chaos, 2009, 19(4): 1357-1366. |
| [11] | 孙克辉, 杨静利, 丁家峰, 等. 单参数Lorenz混沌系统的电路设计与实现[J]. 物理学报, 2010, 59(12): 8385-8392. Sun K H, Yang J L, Ding J F, et al. Circuit design and implementation of Lorenz chaotic system with one parameter[J]. Acta Physica Sinica, 2010, 59(12): 8385-8392. |
| [12] | 叶正伟. 基于FPGA的简化Lorenz混沌系统的PRSG的设计与实现[D]. 长沙: 中南大学, 2013. Ye Z W. Design and implementation of PRSG of the simplified Lorenz chaotic system based on FPGA[D]. Changsha: Central South University, 2013. |
| [13] | 孙克辉, 丘水生, 尹林子. 混沌系统的自适应函数投影同步与参数辩识[J]. 信息与控制, 2010, 39(3): 326-331, 341. Sun K H, Qiu S S, Yin L Z. Adaptive function projective synchronization and parameter identification for chaotic systems[J]. Information and Control, 2010, 39(3): 326-331, 341. |
| [14] | 原冠秀. 一个简化Lorenz混沌系统的active同步控制[J]. 科技视界, 2011(24): 62, 74. Yuan G X. Active synchronization control of a simplified Lorenz system[J]. Science & Technology View, 2011(24): 62, 74. |
| [15] | 方洁, 胡智宏, 江泳. 耦合混沌系统自适应修正函数投影同步[J]. 信息与控制, 2013, 42(1): 39-45. Fang J, Hu Z H, Jiang Y. Adaptive modified function projective synchronization of coupled chaotic system[J]. Information and Control, 2013, 42(1): 39-45. |
| [16] | 薛怀庆, 彭建奎, 安新磊, 等. 分数阶混沌系统全状态混合投影同步及在保密通信中的应用[J]. 信息与控制, 2013, 42(2): 229-235. Xue H Q, Peng J K, An X L, et al. Full state hybrid projective synchronization of fractional-order chaotic systems and its application to secure communication[J]. Information and Control, 2013, 42(2): 229-235. |
| [17] | 李战国, 徐伟. 不同阶混沌系统缩阶混合函数投影同步[J]. 信息与控制, 2012, 41(1): 33-37. Li Z G, Xu W. Reduced-order hybrid function projective synchronization between different-order chaotic systems[J]. Information and Control, 2012, 41(1): 33-37. |
| [18] | Chen G, Lewis F L. Distributed adaptive tracking control for synchronization of unknown networked Lagrangian systems[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2011, 41(3): 805-816. |
| [19] | Ĉelikovský S, Chen G R. On a generalized Lorenz canonical form of chaotic systems[J]. International Journal of Bifurcation and Chaos, 2002, 12(8): 1789-1812. |
| [20] | Sun K H, Liu X, Zhu C X. Dynamics of a strengthened chaotic system and its circuit implementation[J]. Chinese Journal of Electronics, 2014, 23(2): 353-356. |



