2. 安徽检测技术与节能装置省级实验室, 安徽 芜湖 241000
2. Anhui Key Laboratory of Detection Technology and Energy Saving Devices, Wuhu 241000, China
1 引言
1990年人类基因组计划正式启动后,基因芯片技术为生物信息学的研究提供了大量的生物体基因表达数据,推动了基因表达的研究. 基因调控网络(genetic regulatory networks,GRNs)由蛋白质、 蛋白质复合物及相应的信使RNA(mRNA)作为网络的节点而构成,用以分析基因之间的相互关系. 目前,GRNs主要有贝叶斯网络[1]、 布尔基因网络[2]和微分方程等模型.
GRNs的微分方程模型将细胞中的mRNA和蛋白质的浓度作为状态变量,能精确地描述细胞的动态行为. 而时滞普遍存在于GRNs之中,是影响其稳定的重要原因之一,Chen等学者通过分析翻译和转录过程中的时滞,建立GRNs的时滞微分方程模型,并采用特征方程法研究时滞GRNs的稳定性问题[3]. 随后判断时滞GRNs网络的稳定性的充分条件相继被提出[4, 5, 6, 7].
马尔可夫型GRNs由于能够精确地描述不同阶段转录和翻译的变化情况而备受广大学者所关注,研究包含稳定性分析[8, 9]、 状态估计[10]、 H∞滤波[11]等问题. 需要指出的是: 目前关于马尔可夫型GRNs的主要结论均以基于马尔可夫跳变系统的转移概率矩阵已知为前提,该假设条件比较理想,不具有普遍性. 尽管马尔可夫型GRNs的状态转移概率矩阵可以通过统计学的方法获得[12],但GRNs的数据获取困难、 成本代价过高等原因,使得在建立马尔可夫型GRNs模型的过程中适时地放弃部分转移概率的信息是必要的和切合实际的,而此时部分转移概率未知的马尔可夫型GRNs的稳定性问题就变得至关重要.
基于文[13, 14]分离未知转移速率矩阵元素的思想,考虑到时滞对于系统稳定性的影响,本文基于李亚普诺夫稳定性理论,对转移概率缺失的时滞马尔可夫型GRNs的稳定性问题展开研究,为了降低时滞相关稳定性判据的保守性,在构造包含时滞信息的增广李亚普诺夫函数的基础上,弱化李亚普诺夫函数的构造条件,并采用广义的Wirtinger′s不等式处理李亚普诺夫函数弱无穷小算子中的交叉项,进而提出低保守性的马尔可夫型GRNs时滞相关稳定性判据.
符号说明: Rn和Rn×m分别表示n维欧几里德空间和n×m的实矩阵集合; P>0表示P为对称正定实矩阵; E{·}表示数学期望; 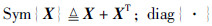 表示对角矩阵; 对于向量x、 y,符号
表示对角矩阵; 对于向量x、 y,符号 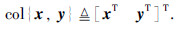 .
.
时滞马尔可夫型GRNs描述如下:
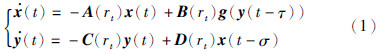
假设1 非线性泛函g(y(t))=[gi(yi(t))]满足:
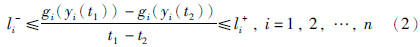
注1 文[15, 16]指出L-和L+的元素可以任意取值,减少了GRNs的约束条件,但是却忽略了减少GRNs的约束条件是否保证系统存在解; 而文[17]明确指出,L-和L+的元素必须是非负实数.
{rt}(t≥0)为有限集合S={1,2,…,N}上的右连续马尔可夫过程,其转移速率矩阵为

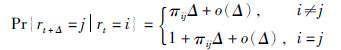
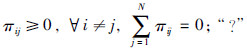 表示切换模态之间的未知转移速率.
表示切换模态之间的未知转移速率.
作用在李亚普诺夫函数V(x(t),y(t),t,i)的马尔可夫过程弱无穷小算子定义为[18, 19]
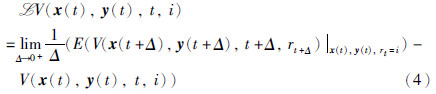
定义1 系统(1)是随机渐近稳定的,若任意初始条件x0∈Rn,y0∈Rn,r0∈S满足下列条件:
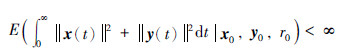
引理1 任意适当维数的矩阵R>0,实数a、 b(a>b)及定义在区间[b,a]→Rn的向量函数x(t),下列不等式成立:
Jensen不等式[20]:
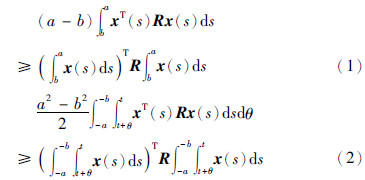
广义Wirtinger′s不等式[21]:
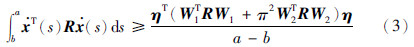
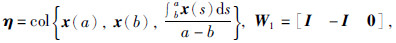
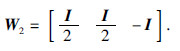
此外,如下符号在文中将被用到:
(1) 集合符号: Ui=Uik∪Uiuk,i∈S,其中,Uik={j: πij已知,j∈S},Uiuk={j: πij已知,j∈S}.
(2) 矩阵符号:
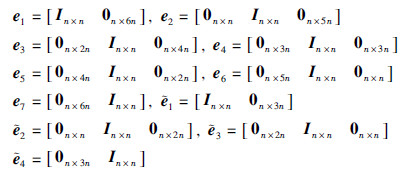
本节对部分转移概率缺失的时滞马尔可夫型GRNs的稳定性问题开展研究,首先给出马尔可夫型GRNs的时滞相关稳定性条件.
定理1 给定正实数σ、 τ,如果存在适当维数的矩阵变量Pi=PTi(i∈S),正定矩阵Q、 R、 S、 Z及对角矩阵Λ=diag{d1,d2,…,dn}≥0,使得对于任意i∈S下列线性矩阵不等式(LMIs)均成立:
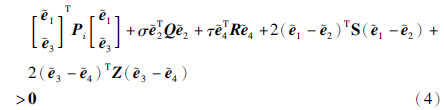
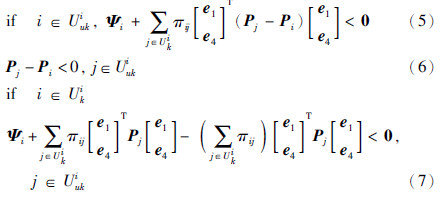
其中,
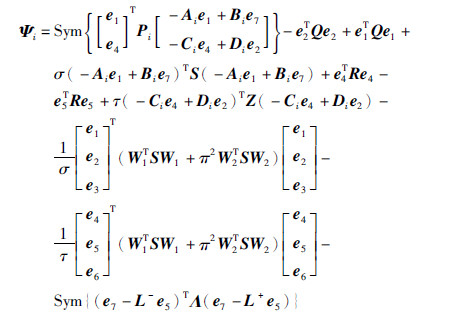
证明 考虑翻译过程和转录过程中的时滞信息,构造增广李亚普诺夫函数:
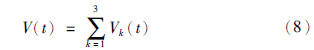
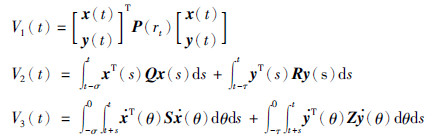
 .
.
由于待定矩阵Pi(i∈S)仅为对称矩阵,所构造的李亚普诺夫函数V(t)不一定为正,不满足李亚普诺夫稳定性理论的条件,故整个定理的证明分2步完成.
第1步 定理1的条件能够保证李亚普诺夫函数V(t)>0.
由引理1知,下列不等式成立:
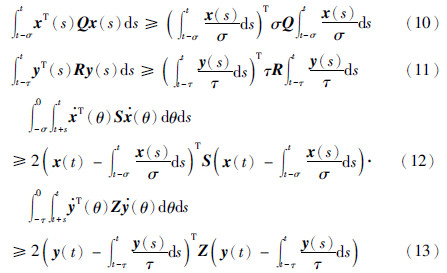
由LMI(5)知李亚普诺夫函数V(t)>0.
第2步 定理1的条件能够保证李亚普诺夫函数的弱无穷小算子  .
.
李亚普诺夫函数Vk(t)(k=1,2,3)的弱无穷小算子分别为
采用广义Wirtinger′s不等式处理式(16)中的积分项得
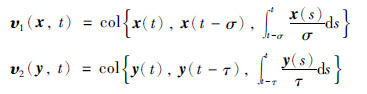
由于非线性泛函g(y(t-τ))必须满足约束条件(2)以保证系统(1)存在唯一解,故对于∀Λ=diag{d1,d2,…,dn}≥0下列不等式成立:
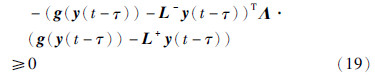
将不等式(18)~(20)应用到李亚普诺夫函数的弱无穷小算子  中,可得
中,可得
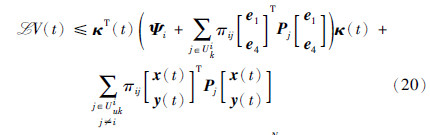
因为πij≥0,j≠i且 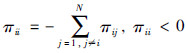 ,根据πii是否已知,分两种情况进行讨论:
,根据πii是否已知,分两种情况进行讨论:
(i) 若i∈Uiuk,由状态转移速率矩阵每行元素之和为0可知,下列零式恒成立:
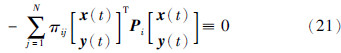
将式(21)应用到式(20)中,可得
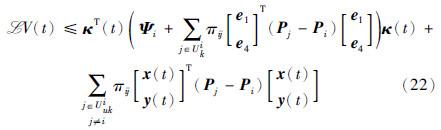
其中,
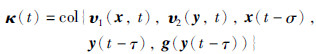
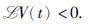 .
.
(ii) 若i∈Uik,由πij≥0,j≠i且 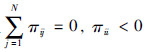 可知
可知 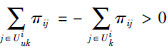 从而由式(20)得
从而由式(20)得
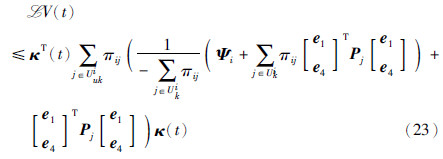
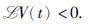 ,即定理1为马尔可夫型GRNs(1)是随机渐近稳定的充分条件. 证毕.
,即定理1为马尔可夫型GRNs(1)是随机渐近稳定的充分条件. 证毕.
注2 本节所构造的李亚普诺夫函数有两个特点: ① 在李亚普诺夫函数中引入了增广项 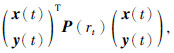
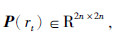 ,不仅表征GRNs节点处的mRNA与mRNA、 蛋白质与蛋白质浓度之间的关系,还体现了mRNA与蛋白质之间可能存在的交互影响. ② 与已有结论要求P(rt)必须是对称正定相比,李亚普诺夫函数中P(rt)只要求是对称矩阵,降低了李亚普诺夫函数中P(rt)的约束条件.
,不仅表征GRNs节点处的mRNA与mRNA、 蛋白质与蛋白质浓度之间的关系,还体现了mRNA与蛋白质之间可能存在的交互影响. ② 与已有结论要求P(rt)必须是对称正定相比,李亚普诺夫函数中P(rt)只要求是对称矩阵,降低了李亚普诺夫函数中P(rt)的约束条件.
若马尔可夫过程的有限集合S={1},则马尔可夫型GRNs可表述一般意义上的双时滞GRNs:
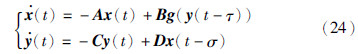
推论1 给定正实数σ、 τ,如果存在适当维数的矩阵P=PT,正定矩阵Q、 R、 S、 Z及对角矩阵Λ=diag{d1,d2,…,dn}≥0,使得下列LMIs均成立:
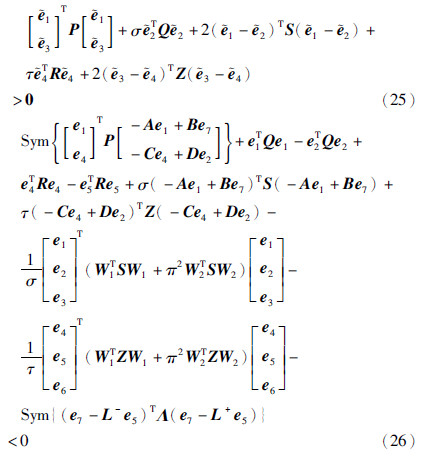
则双时滞GRNs (24)是全局渐近稳定的.
4 数值例子例1 考虑如下的4模态马尔可夫型GRNs,其系统矩阵参数为

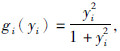 ,则L-1,L-2,L-3,L-4为零矩阵,L+1=L+2=L+3=L+4=diag{0.65,0.65,0.65,0.65,0.65}. 状态转移速率矩阵为
,则L-1,L-2,L-3,L-4为零矩阵,L+1=L+2=L+3=L+4=diag{0.65,0.65,0.65,0.65,0.65}. 状态转移速率矩阵为
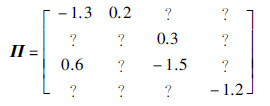
利用本文定理1获得不同时滞情况下最大允许时滞上界σ和τ见表 1.
| 最大允许时滞σ | 0.893 5 | 1.161 7 | 0.5 |
| 最大允许时滞τ | 0.893 5 | 0.5 | 1.639 5 |
鉴于马尔可夫型GRNs的模态切换存在随机性,本文基于蒙特卡罗分析方法,分别给出在时滞σ=τ=0.893 5,在初始状态为x0=[3-4 2 0.8 4]T和y0=[-0.630.4 0.5 0.28 0]T情况下,500次随机切换状态下的表示mRNA和蛋白质的状态响应轨迹见图 1和图 2.
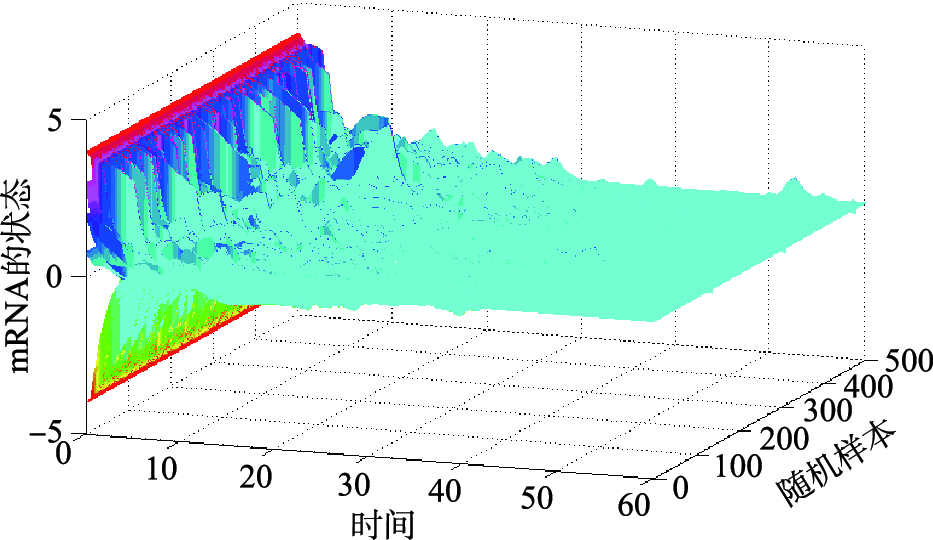 |
| 图 1 500次随机样本的mRNA状态响应轨迹Fig. 1 State responses of mRNA with 500 random samplings |
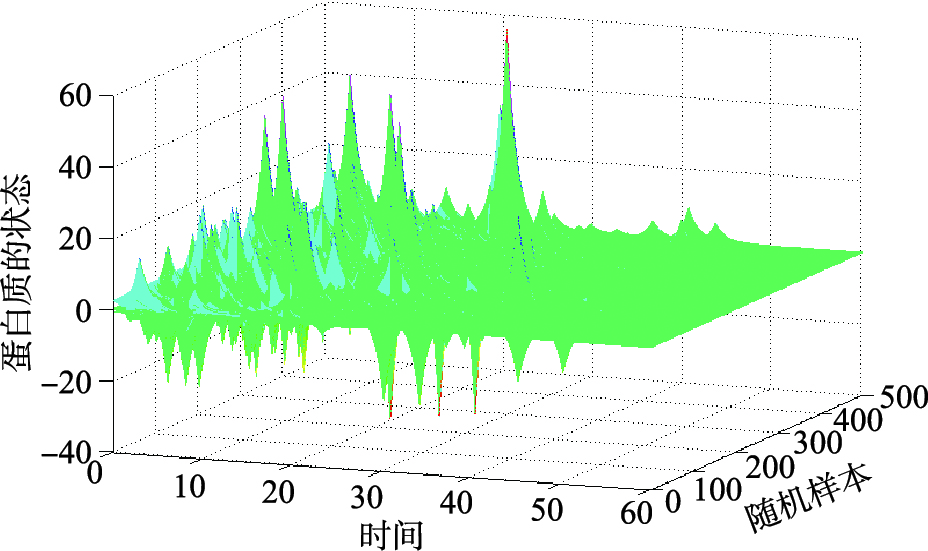 |
| 图 2 500次随机样本的蛋白质状态响应轨迹Fig. 2 State responses of proteins with 500 random samplings |
例2 考虑GRNs (24),其系统矩阵参数为[6]
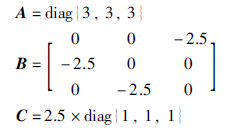
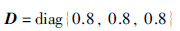
非线性反馈调节泛函与例1相同,则L-为零矩阵,L+=diag{0.65,0.65,0.65}.
利用文[6]的定理1和文本的推论1分别获得最大允许时滞上界和变量个数,如表 2所示.
表 2的时滞上界对比结果表明: 本文所提方法具有较低的保守性; 而变量个数的对比表明,与文[6]相比,推论1大大降低了LMIs求解计算的复杂度.
5 结论考虑翻译和转录中的时滞是造成GRNs不稳定的主要因素之一和GRNs的数据获取困难这两个因素,本文针对基于缺陷统计的马尔可夫型GRNs的随机稳定性问题展开研究,提出具有低保守性的GRNs的时滞相关稳定性判据,而数值分析及仿真验证了该判据的有效性和优越性. 同时,本文也为研究转移概率不确定的马尔可夫型GRNs的稳定性分析和综合问题提供一种有效的分析方法.
| [1] | Perrin B E, Ralaivola L, Mazurie A, et al. Gene networks inference using dynamic Bayesian networks[J]. Bioinformatics, 2003, 19(sup. 2): ii138-ii148. |
| [2] | Müssel C, Hopfensitz M, Kestler H A. BoolNet-an R package for generation, reconstruction and analysis of Boolean networks[J]. Bioinformatics, 2010, 26(10): 1378-1380. |
| [3] | Chen L, Aihara K. Stability of genetic regulatory networks with time delay[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 2002, 49(5): 602-608. |
| [4] | Chesi G. Robustness analysis of genetic regulatory networks affected by model uncertainty[J]. Automatica, 2011, 47(6): 1131-1138. |
| [5] | Ren F, Cao J. Asymptotic and robust stability of genetic regulatory networks with time-varying delays[J]. Neurocomputing, 2008, 71(4/5/6): 834-842. |
| [6] | Liu P L. Robust stability analysis of genetic regulatory network with time delays[J]. ISA Transactions, 2013, 52(3): 326-334. |
| [7] | 何勇, 曾进, 吴敏, 等. 具有区间时滞的离散时间基因调控网络稳定性研究[J]. 控制理论与应用, 2012, 29(11): 1465-1470. He Y, Zeng J, Wu M, et al. Stability for discrete-time genetic regulatory networks with time-varying interval delays[J]. Control Theory & Applications, 2012, 29(11): 1465-1470. |
| [8] | Balasubramaniam P, Rakkiyappan R, Krishnasamy R. Stochastic stability of Markovian jumping uncertain stochastic genetic regulatory networks with interval time-varying delays[J]. Mathematical Biosciences, 2010, 226(2): 97-108. |
| [9] | Zhang D, Yu L. Passivity analysis for stochastic Markovian switching genetic regulatory networks with time-varying delays[J]. Communications in Nonlinear Science and Numerical Simulation, 2011, 16(8): 2985-2992. |
| [10] | Lee T H, Lakshmanan S, Park J H, et al. State estimation for genetic regulatory networks with mode-dependent leakage delays, time-varying delays, and Markovian jumping parameters[J]. IEEE Transactions on NanoBioscience, 2013, 12(4): 363-375. |
| [11] | Mohammadian M, Abolmasoumi A H, Momeni H R. H∞mode-independent filter design for Markovian jump genetic regulatory networks with time-varying delays[J]. Neurocomputing, 2012, 87(15): 10-18. |
| [12] | Liang J L, Lam J, Wang Z D. State estimation for Markov-type genetic regulatory networks with delays and uncertain mode transition rates[J]. Physics Letters A, 2009, 373(47): 4328-4337. |
| [13] | Zhang Y, He Y, Wu M, et al. Stabilization for Markovian jump systems with partial information on transition probability based on free-connection weighting matrices[J]. Automatica, 2011, 47(1): 79-84. |
| [14] | Guo Y F, Zhu F L. New results on stability and stabilization of Markovian jump systems with partly known transition probabilities[J]. Mathematical Problems in Engineering, 2012(S1): 1-11. |
| [15] | Wang W Q, Zhong S M, Nguang S K, et al. Novel delay-dependent stability criterion for uncertain genetic regulatory networks with interval time-varying delays[J]. Neurocomputing, 2013, 121(18): 170-178. |
| [16] | Lou Y H, Ye Q, Cui B T. Exponential stability of genetic regulatory networks with random delays[J]. Neurocomputing, 2010, 73(4/5/6): 759-769. |
| [17] | 张艳. 基于自由连接权矩阵的Markov切换系统鲁棒控制[D]. 长沙: 中南大学, 2012. Zhang Y. Robust control for Markov switching system based on free-connection weighting matrices[D]. Changsha: Central South University, 2012. |
| [18] | Kushner H J. Stochastic stability and control[M]. New York, USA: Academic Press, 1967. |
| [19] | Skorohod A V. Asymptotic methods in the theory of stochastic differential equation[M]. Providence, RI, USA: American Mathematical society, 1989. |
| [20] | Sun J, Liu G P, Chen J. Delay-dependent stability and stabilization of neutral time-delay system[J]. International Journal of Robust and Nonlinear Control, 2009, 19(12): 1364-1375. |
| [21] | Seuret A, Gouaisbaut F. Wirtinger-based integral inequality: Application to time-delay systems[J]. Automatica, 2013, 49(9): 2860-2866. |



