在网络化控制系统(networked control systems,NCS)中系统经常需要传送信号到一个相对较远的地方,以构成一个闭环反馈系统来实现某些控制目标,这类系统有微型电机系统、 传感器网络、 移动电话和一些工业化控制网络等,近几年取得了不少成果[1, 2]. 通常这一类系统会包括一个数字通信信道作为其组成部分,当传感器获得一个所需机构的物理量时,它会将这些信息通过这个信道传递到另一个地方的控制模块. 信息被量化编码后再传输,这个过程引入了量化误差. 量化反馈控制在控制领域不是一个新方向,有很多研究量化策略和系统稳定性来达到一些特定性能的工作和成果,这个课题现在仍然很有价值. 文[3]给出了量化反馈控制的一个概述,并且展示了这个领域中其他学者的一些重要工作成果. 量化器根据是否动态变化分为动态量化器和静态量化器两类,动态量化器通过计算生成一个不确定集合序列,假定在每个时刻状态都落在指定的不确定集合中,量化器将当前不确定集合依据量化比特数分为若干小集合,将信号所处小集合序号作为结果发给控制器,控制器根据量化算法估计测量信号,由此计算控制量. 假定量化器知道控制量,它就可以估计下一步测量信号所处范围,从而更新下一步的不确定集合. 在文[4, 5, 6]中,作者提供了一些动态量化策略并分析了误差的收敛,例如文[5]研究了线性离散时间系统的动态量化问题,给出了基于空间分割方法的控制量化误差方法. 对比静态量化器,动态型的有更好的性能,但是编码器解码器需要拥有内存空间并且结构更复杂. 在量化器这部分,文[7, 8]研究静态量化器并使用最粗糙量化器,即对数型的量化器,这种量化器信号量越大量化误差越大. 静态量化器不能把误差减小到0,除非量化层数是无限的,因此只能达到一种实用稳定性.
在另外一方面,嵌入式和网络控制系统通常是基于周期性采样来传输数据. 有人指出这种模式并不需要一个控制系统多次执行. 采用相对保守的方法会导致一些在系统实现中不必要的采样. 因此,人们对结合实时系统和控制方法很感兴趣,适应任务特性和调度任务等证明了反馈控制原理能够减少实时系统在控制任务周期中的敏感度,降低对时间控制的要求.
事件触发采样是一种结合实时系统和控制系统性能的方法,该方法使得系统的任务周期适应了某个指标的性能[9]. 这类系统中最典型的一种是系统只在某个指标的误差超过了一个特定的阈值时执行控制任务,这就意味着只有当系统的性能需要维持时实时系统才被使用到. 所以这种零散发生的控制任务集的平均频率会比具有可比性的周期采样系统的任务集频率要低. 文[10]给出了2种采样系统的对比,展示了事件触发采样系统和周期采样系统要获得相同误差的均方差值,对比可知事件触发采样系统需要的平均采样周期会更短.
在事件触发采样中还有一些比较重要的工作,Tabuada[11]研究了控制任务的调度和系统状态变化率是Lipschitz连续情况下的一类系统内部执行时间的下界. 一个符合有限增益L2稳定性的自身触发反馈控制系统在文[12]中进行了研究. 线性系统中与自触发相关的一些工作可以参考文[13, 15],文[16]研究了事件触发随机系统中的最优控制和估计问题. 接下来,文[17]将事件触发控制扩展到了分布式的网络控制系统中,用来减少在NCS中传递信息的拥塞,并且考虑了丢包和传递时延的问题,但没有考虑引入的量化器.
基于这些已有的方法,考虑对一个量化反馈控制系统使用事件触发控制来达到一种类似L2稳定性且比固定周期采样有一个更好的采样间隔性能. 近些年也有一些文献研究将量化器和事件触发控制结合的控制系统,比如文[18, 19]考虑传感器对被控系统进行周期采样,然后将信息交由事件触发模块判断,当条件符合时信息被量化然后经数字信道传输,更新控制器输入,使系统达到稳定. 本文方法虽然在对系统状态量检测上是连续的,但更新控制器在频率上有性能优势,而且在本地对系统状态检测的代价十分低,因此能节省更大的资源.
2 系统模型本节首先介绍一些基本定义、 符号和系统模型,并对问题进行数学上描述.
状态量x是一个在时间上的映射量,定义为x: R→Rn,是一个向量. ║x(t)║表示通常的欧几里得范数,$\sqrt{\int{_{0}^{\infty }\parallel x\left( \tau \right){{\parallel }^{2}}d\tau }}$表示2-范数,L2表示所有2-范数有界的可测函数构成的线性空间. 这里引入L2稳定性,通常考虑一类在2个L2空间中的映射G: L2→L2,其中w∈L2是输入,Gw∈L2是系统输出,如果存在有限正实数γ和β满足式(1),那么系统满足L2稳定.
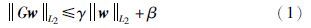
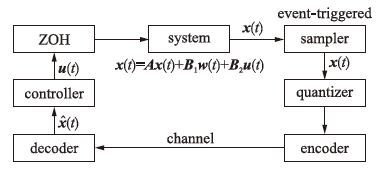
这个量化反馈系统如图 1中所示,考虑事件触发无时延情况,ZOH代表零阶保持器,其保持控制量不变直至下一次触发,数字信道是一个理想信道,无丢包时延等发生,${\hat{x}}$(t)代表状态量被量化后的值.
|
| 图 1 系统结构 Fig. 1 System structure |
系统状态方程如下:
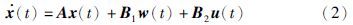
下面一条引理是在无量化器下的事件触发控制条件,能使系统达到L2稳定性. 首先引入哈密尔顿—雅可比不等式(Hamilton-Jacobi inequality,HJI). 假设存在一个实数常数γ>0和一个正定连续可微函数V: Rn→R满足:
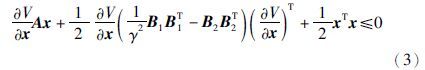
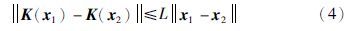
引理1 [14] 线性微分方程(2)初始条件为x(0)=x0∈Rn且w: R→Rp是一个在L2空间的外部扰动,u: R→Rm在第j个任务的连续时间中取:
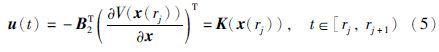
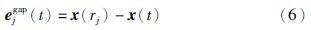
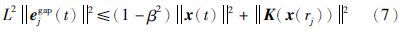
这个引理提供了一种达到L2稳定性的方法,引理的证明参考文[14],本文在此基础上增加了量化误差.
2.2 对数量化器量化器部分我们选择静态对数量化器,动态对数量化器在编码率上有更好性能,对于后面分析基于事件触发的量化反馈控制系统稳定性时,这2种量化器情况基本一致. 本文定理中使用静态对数量化器,动态对数量化器的情况本文只给出其定义和对最后结果稍作分析. 下面是2种量化器的定义:
静态对数量化器可以看作一个映射f: x→z,即:
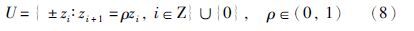
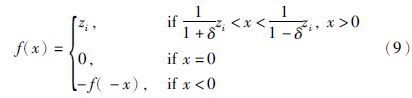

动态对数量化器定义[20]: 编码比特数B,量化密度σ∈(0,1)和缩放参数a>0这几个参量构成一个映射Q(a,·),将某区间内的被编码量映射为
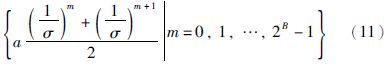
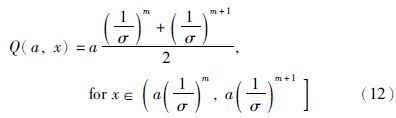
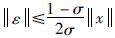 ,对于负的值则可以多取一位编码位判断符号,然后取相反来编码. 动态量化策略如下:
,对于负的值则可以多取一位编码位判断符号,然后取相反来编码. 动态量化策略如下:
1) 如果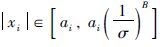 ,则量化器不变,直接量化.
,则量化器不变,直接量化.
2) 如果|xi|<ai,那么进行缩小,让ai=(σ)aiB,发送缩小指令信号,直到满足1)后量化.
3) 如果x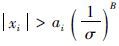 ,那么进行放大,让ai=($\frac{1}{\sigma }$)aiB,发送放大指令信号,直到满足1)后量化.
,那么进行放大,让ai=($\frac{1}{\sigma }$)aiB,发送放大指令信号,直到满足1)后量化.
在接收端则根据有无收到缩小或放大指令做相应调整,然后得出相应量化值.
对于均匀量化器,由于量化误差不满足一些性质,目前在我们的方法中暂不适用.
3 带量化的事件触发采样控制系统在本节给出一个使得量化采样系统通过事件触发控制达到L2稳定性的充分条件. 对给出的条件,当系统破坏这个不等式时,传感器进行采样传送数据,然后控制器在一个新的执行时间中更新输出,通过这种方法,期望得到一个比传统周期采样更长的执行时间. 相比文[14],这部分内容多引入了量化误差的影响,通过对原方法的扩展,将量化误差作为加性项,推导出触发条件的不等式左侧在事件触发时即更新控制器时一定再次符合事件触发的条件,使得系统在有量化误差情况下实现事件采样控制.
带量化的事件采样控制系统会有两种误差,下面定义这两种不同性质误差. 第1种是当前状态值的量化误差,定义为eq(t)=${\hat{x}}$(t)-x(t); 第2种是量化后时间上累积产生的误差,这种误差定义为${\hat{e}}$gap(t)=(${\hat{x}}$rj)-${\hat{x}}$(t),是量化器在每个执行期间的开始时刻rj量化值与当前时刻状态量化值的差值,${\hat{x}}$(rj)是量化后的状态,这两个误差的获得需要传感器监视系统状态量来获得.
把引理1中的系统扩展为带量化反馈的系统,结构如图 1所示,然后得出定理1.
定理1 线性微分方程(2)初始条件x(0)=x0∈Rn,量化器是密度为ρ的静态对数量化器,控制器取如下形式:
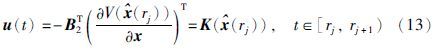
那么系统是L2稳定的充分条件为:
保证量化密度:

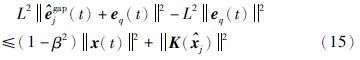
证明 先求V的方向导数:
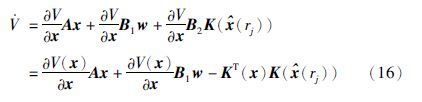
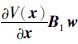 作为平方项的交叉项得到:
作为平方项的交叉项得到:
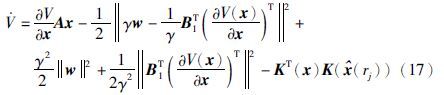
 ,得
,得
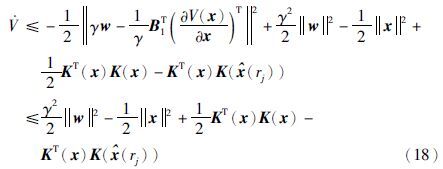
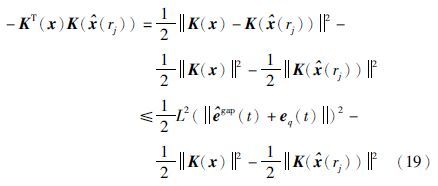
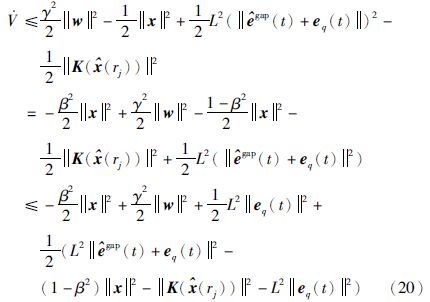
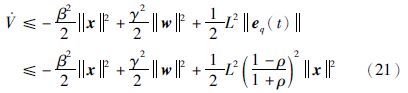
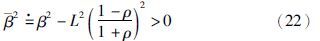
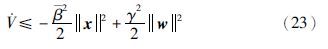
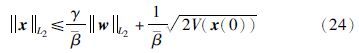
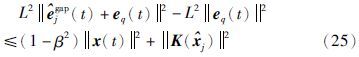
注1 当系统状态量趋近于0时,由于扰动存在,可能会导致频繁地触发采样条件,这会使采样频率性能变得很差,一种解决办法就是引入一个下界作为触发条件[14]:
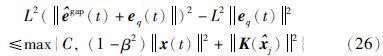
注2 在事件触发采样系统中,量化密度ρ和参数β与平均采样周期正相关. 一方面,由于量化密度越高,控制量越接近所需值,因此可以减少控制次数,但对应的代价是需要的编码位数变多; 另一方面,β的选取也会影响事件采样平均周期,若适当缩短可以增大事件触发平均采样周期,但会降低系统L2性能,所以要适当选取.
注3 对于前面提到的动态对数量化器,在该定理中同样适用,将动态对数量化器的量化误差与状态量关系特性代入式(22)中,得到对量化密度σ∈(0,1)的约束σ>L/(L+2β),区别于静态对数量化器,动态对数量化器在量化值传递时需要更少的编码位数,然而在定理中这部分不影响触发条件,因此采用静态对数量化器.
定理1给出了在有量化器引入量化误差的情况下事件采样时触发的条件,同时给出了对数量化器的一个选择参考标准.
4 仿真结果对于一个简单的线性二阶系统,本文采用推导的条件进行事件触发来控制并验证稳定性,与固定采样周期的控制对比,结果表明采用事件触发方法在采样频率上的效果更好,系统状态空间方程如下:
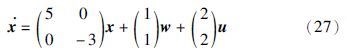
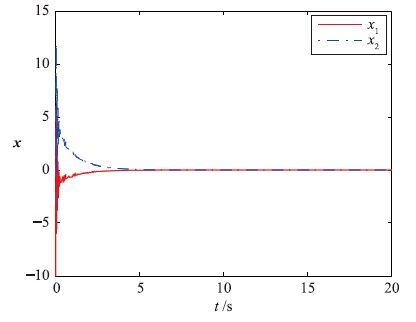
|
| 图 2 事件触发采样系统状态量 Fig. 2 States of event-triggered sampling system |
在相同控制器,量化器和初始值下,对比采样周期为0.028 s的控制方式,对应被控量变化如图 3所示.
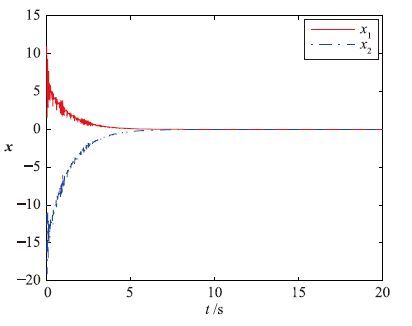
|
| 图 3 周期采样系统状态量 Fig. 3 States of perodic sampling system |
由图 2和图 3对比可知,这两种方式都能让系统在有量化误差情况下达到稳定. 对比两者收敛速率,事件触发下,系统经过约10.0 s使状态量收敛到稳态; 周期采样下,经过约13.0 s使状态量收敛到稳态,因此事件触发下收敛更快. 在稳态情况下进行性能对比,以15 s至20 s这段时间状态量x的欧几里得范数的标准方差大小进行比较,事件触发为5.016 1×10-5s,定周期为5.391 2×10-5s,因此事件触发稳态性与定周期稳态性相当或稍好. 在稳态响应15 s至20 s这段时间内,统计采样频率可知事件触发采样147次,平均采样周期0.034 s,而定周期采样178次,平均采样周期0.028 s,相比之下事件触发采样次数更少.
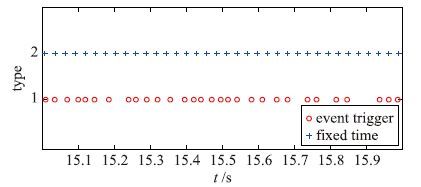
对比仿真图 4中截取了15 s到16 s的一段展示,每个点为一次采样控制,纵坐标为1的是事件触发的模式,纵坐标为2的是定周期模式,可以看出在一段相同时间内,事件触发采样次数比定周期采样次数少. 经统计在0 s到20 s内,使用事件触发机制采样490次,平均采样周期0.040 8 s; 定周期采样714次,平均采样周期0.028 s. 事件触发的平均周期长了42%,可以得出事件触发采样在量化系统中比定周期采样方法在采样频率上性能更优,这是因为事件触发是从系统稳定性需求分析出何时采样,可以适当减少采样次数.
|
| 图 4 对比采样时间 Fig. 4 Comparison of sampling time |
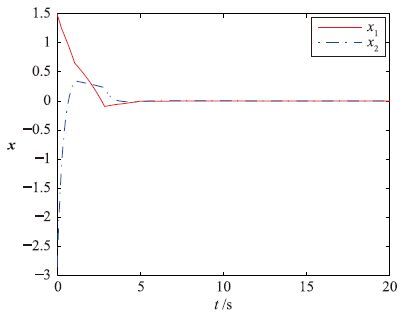
在相关领域内,本文方法仍有一定优势,如在第一节中提过的对本地系统状态量进行周期采样,再经事件触发机制量化控制的方法也是解决这类问题,下面对其中文[15]进行性能对比,我们选取其仿真中同一被控系统:
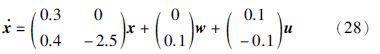
|
| 图 5 系统状态量 Fig. 5 States of the system |
|
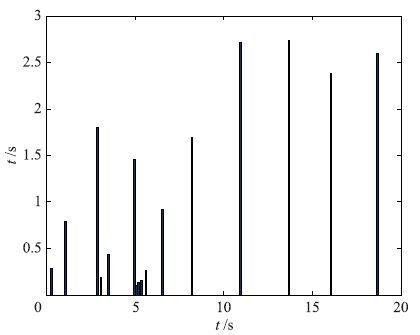
| 图 6 采样间隔 Fig. 6 Sampling intervals |
经统计本文的平均采样周期为1.25 s,文[15]中平均采样周期为0.369 6 s,故采样性能更优,并且控制器设计方法也较为简单. 原文中的优势是通过周期采样获得系统状态量,本文是实时监测获得,但本地获得状态值信息代价并不大,因而可以用本文方法改善控制频率.
5 总结本文把事件触发的方法应用在量化反馈控制中,成功获得了使得系统达到L2稳定性的新的事件触发条件,并且给出了对数量化器的量化密度ρ的约束条件. 然后在仿真中将其与带量化器的定周期采样的相同系统的采样频率的性能进行对比,验证了与事件触发结合后能获得更优的性能,在动态响应和稳态响应以及采样频率上性能都有一定的提升,能在实际控制中节省在一定的采样次数上的开销,并与同领域文献进行性能对比,得出该方法在采样频率上能取得更优性能.
| [1] | 邢江, 关治洪. 网络化控制系统的研究现状与展望[J]. 控制工程, 2006, 13(4): 294-297. Xing J, Guan Z H. Research progress and prospects of the networked control systems[J]. Control Engineering of China, 2006, 13(4): 294-297. |
| [2] | Hu H L, Shao Q K. Non-uniformly sampling control of networked control systems with communication constraints[J]. Information and Control, 2013, 42(3): 320-326. |
| [3] | Nair G N, Fagnani F, Zampieri S, et al. Feedback control under data rate constraints: An overview[J]. Proceedings of the IEEE, 2007, 95(1): 108-137. |
| [4] | Brockett R W, Liberzon D. Quantized feedback stabilization of linear systems[J]. IEEE Transactions on Automatic Control, 2000, 45(7): 1279-1289. |
| [5] | Tatikonda S, Mitter S. Control-under communication constraints[J]. IEEE Transactions on Automatic Control, 2004, 49(7): 1056-1068. |
| [6] | Liberzon D. On stabilization of linear systems with limited information[J]. IEEE Transactions on Automatic Control, 2003, 48(2): 304-307. |
| [7] | Yu H, Antsaklis P J. Event-triggered output feedback control for networked control systems using passivity: Achieving L2 stability in the presence of communication delays and signal quantization[J]. Automatica, 2013, 49(1): 30-38. |
| [8] | Guan Y, Han Q L, Peng C. Event-triggered quantized-data feedback control for linear systems[C]//2013 IEEE International Symposium on Industrial Electronics (ISIE). Piscataway, NJ, USA: IEEE, 2013: 1-6. |
| [9] | Garcia E, Antsaklis P J. Model-based event-triggered control for systems with quantization and time-varying network delays[J]. IEEE Transactions on Automatic Control, 2013, 58(2): 422-434. |
| [10] | Astrom K J, Bernhardsson B M. Comparison of riemann and lebesgue sampling for first order stochastic systems[C]//Proceedings of the 41st IEEE Conference on Decision and Control. Piscataway, NJ, USA: IEEE, 2002: 2011-2016. |
| [11] | Tabuada P. Event-triggered real-time scheduling of stabilizing control tasks[J]. IEEE Transactions on Automatic Control, 2007, 52(9): 1680-1685. |
| [12] | Wang X F, Lemmon M D. Self-triggered feedback control systems with finite-gain stability[J]. IEEE Transactions on Automatic Control, 2009, 54(3): 452-467. |
| [13] | Mazo M, Anta A, Tabuada P. An ISS self-triggered implementation of linear controllers[J]. Automatica, 2010, 46(8): 1310-1314. |
| [14] | Lemmon M. Event-triggered feedback in control, estimation, and optimization[M]. London: Springer-Verlag, 2010: 293-358. |
| [15] | Mazo M, Tabuada P. Input-to-state stability of self-triggered control systems[C]//Proceedings of the 28th Chinese Control Conference on Decision and Control. Piscataway, NJ, USA: IEEE, 2009: 928-933. |
| [16] | Xu Y, Hespanha J. Optimal communication logics in networked control systems[C]//Proceedings of the 43rd Conference on Decision and Control. Piscataway, NJ, USA: IEEE, 2004: 1037-1042. |
| [17] | Wang X F, Lemmon M D. Event-triggering in distributed networked control systems[J]. IEEE Transactions on Automatic Control, 2011, 56(3): 586-601. |
| [18] | Liu C, Hao F. Event-triggered dynamic L2 controller design for linear systems with quantized feedback[C]//2014 IEEE Chinese Guidance, Navigation and Control Conference (CGNCC). Piscataway, NJ, USA: IEEE, 2014: 2353-2358. |
| [19] | Guan Y P, Han Q L, Peng C. Event-triggered quantized-data feedback control for linear systems[C]//2013 IEEE International Symposium on Industrial Electronics (ISIE). Piscataway, NJ, USA: IEEE, 2013: 1-6. |
| [20] | Sun Y, Wang X F. Quantization scheme design in distributed event-triggered networked control systems[C]//Proceedings of the 18th IFAC World Congress. Kington, UK: IFAC, 2011: 13257-13262. |



