2. 安徽师范大学网络与信息安全工程技术研究中心,安徽 芜湖 241003
2. Network and Information Security Engineering Research Center, Anhui Normal University, Wuhu 241003, China
无等待流水车间调度(no-wait flowshop scheduling,NWFS)问题是一类重要的约束组合优化问题,广泛存在于炼钢、 化工制造、 食品加工和塑料塑造等工业领域[1]. 该问题可描述为: n个作业在m台机器上按给定加工时间、 顺序进行加工且作业在加工过程中不能被中断. 优化目标有最小化最大完工时间、 总延迟和总完工时间等,其中,最小化总完工时间(total flow time,TFT)是实际应用中的重要指标,TFT最小化可促进资源稳定有效利用、 作业快速周转以及在制品库存最小化. 最小化总完工时间的NWFS问题记为Fm|nwt|∑Ci. 已经证明,在机器数m>2时,该问题为强NP难问题[2].
目前,求解Fm|nwt|∑Ci主要采用启发式算法和智能算法. 启发式算法分为构造启发式和复合启发式. Rajendran等[3]提出了基于任务插入的构造启发式算法,Bertolissi[4]设计了基于比较的构造启发式算法,朱夏等[5]构建了基于目标增量的快速迭代贪婪算法,李亚志等[6]提出了基于插入—分段的复合启发式(insertion-segment based composite heuristic,ISCH)算法,Laha等[7]设计了最新的改进启发式算法(improved heuristic algorithm,IHA),实验结果显示其性能优于复合启发式算法[8, 9],IHA是现阶段较优的启发式算法. 启发式算法尽管求解速度较快,但求解质量一般不太理想. 智能优化算法对Fm|nwt|∑Ci优化表现出高度的有效性. Pan等[10]提出了离散粒子群优化算法(discrete particle swarm optimization algorithm with the variable neighborhood descent local search,DPSOVND),Gao等[11]开发了离散的和声搜索算法(discrete harmony search,DHS),Jarboui等[12]提出了基于变邻域搜索的混合遗传算法(genetic algorithm-variable neighborhood search,GA-VNS),实验结果证明GA-VNS求解质量优于DPSOVND.
萤火虫优化(glowworm swarm optimization,GSO)算法是一种新颖的智能算法,通过模拟萤火虫的社会行为实现优化,具有收敛速度快、 设置参数少、 易于实现及并行设计,广泛应用于工程优化问题[13, 14, 15, 16, 17]. 然而因其寻优能力主要是靠萤火虫个体之间的相互作用和影响,个体自身缺乏变异机制,因而算法存在“早熟收敛”缺陷. 量子进化算法(quantum-inspired evolutionary algorithm,QEA)[18]将量子计算与进化计算相融合,通过量子比特编码、 解码染色体,同时利用当前最优个体信息更新量子旋转门,能加速算法收敛.
为了弥补萤火虫优化算法的不足,将量子进化机制嵌入萤火虫算法中,并与设计的一种局部邻域搜索算法(local neighborhood search,LNS)相融合,提出了基于LNS的量子萤火虫优化(quantum-inspired GSO based on LNS,QGSOLNS)算法,以实现优化性能互补. 将QGSOLNS与几个较优的算法(IHA、 DGSO(discrete GSO)[13]、 GA-VNS及DHS)进行仿真比较,实验结果表明所提算法能高效地求解Fm|nwt|∑Ci问题.
2 问题描述令n个作业在m台机器上加工时间为一个n×m矩阵P,其中Pi,k为作业Ji(i=1,2,…,n)在机器Mk(k=1,2,…,m)上的加工时间. 作业开工时间距离构成一个n×n矩阵D,其中元素Di,j(i,j=1,2,…,n)为相邻两作业Ji和Jj的开工时间距离,规定同一作业间的距离为∞,Di,j计算公式为
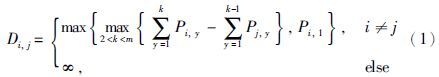
易知,式(1)时间复杂度为O(m). 设S={π1,π2,…,πi-1,πi,…,πn}表示一个调度,其中πi∈{J1,J2,…,Jn}(i=1,2,…,n)表示S的第i个位置上的作业. 在NWFS中,任意2个作业间的距离都是固定的,与具体的调度序列无关. 因此,调度S的总完工时间可按式(2)计算:
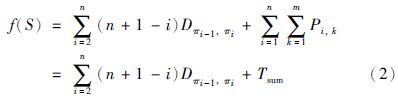
由式(1)和式(2)可知,调度序列中任何2个相邻作业的TFT只与两者的加工时间有关,与其它作业无关. 此外,为了有效地提高算法运行效率,本文所有邻域搜索产生新序列的TFT值均采用目标增量法[5]计算.
本文优化目标可描述为:
∃序列S*∈调度集合Π,对于∀S∈Π,均有f(S*)≤f(S)成立.
3 局部邻域搜索(LNS) 3.1 算法思想由于VNS算法每次迭代要完整地搜索当前解邻域,这在大规模流水调度中会造成算法运行时间大幅增加、 优化性能下降; 另外,当解逼近全局最优时,解中大部分“块”结构[19]均已稳定,重复移动块内作业易破坏“优质”邻域结构,降低求解质量. 鉴于此,本文改进邻域搜索方式,提出了局部邻域搜索算法LNS.
LNS算法只对局部最优解执行一次随机扰动,产生前后邻域结构的变化,并且仅对变化的位置进行搜索,不重复执行完整搜索. LNS算法的基本框架如图 1所示.

|
| 图 1 LNS算法框架 Fig. 1 LNS algorithm framework |
为方便描述,令当前作业调度S={π1,π2,…,πn},并引入虚作业π0为初始作业,πn+1为终止作业,它们在所有机器上的加工时间均为0且不参与调度,此时S={π0,π1,π2,…,πn,πn+1}. 同时,给出如下定义:
定义1 序对交换(pair-exchange): 将S中任意两个作业πi(i=1,2,…,n)和πj(j=1,2,…,n)调换到对方位置,记为Swap(S,i,j).
定义2 序对移位(shift): 将S中的作业πi(i=1,2,…,n)从所在位置删除,再插入到作业πj(j=1,2,…,n)的位置,记为Shift(S,i,j).
定义3 插入点(cut point): 位于S中相邻作业对(πx,πx+1)(x=0,1,…,n)中间的位置.
定义4 邻居作业(neighborhood job): 位于S中某作业πx(x=1,2,…,n)相邻位置的作业.
当前对S执行一次交换或移位后,对应有2种不同局部邻域结构,如图 2和图 3所示.
|
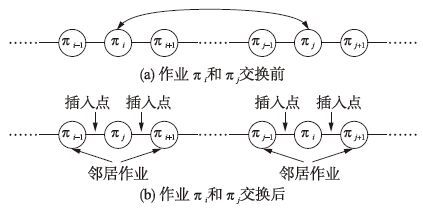
| 图 2 局部邻域序对交换结构图 Fig. 2 Structure of local neighborhood for pair-exchange |
|
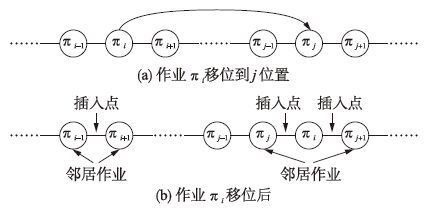
| 图 3 局部邻域移位结构图 Fig. 3 Structure of local neighborhood for shift |
在图 2中,作业πi与πj(i,j=1,2,…,n)交换后,调度作业A={πi,πj},A的邻居作业V={πi-1,πi+1,πj-1,πj+1},对应插入点CP={(πi-1,πj),(πj,πi+1),(πj-1,πi),(πi,πj+1)}; 在图 3中,作业πi移位到位置j后,A={πi},V={πi-1,πi+1,πj,πj+1},CP={(πi-1,πi+1),(πj,πi),(πi,πj+1)}. 剩余作业U=S-A-V.
上述A、 V(剔除虚作业π0和πn+1)中任一作业均可与非自身作业构成序对进行交换或移位,U中任一作业也可移位至CP中任一插入点处; 然后评估所述全部操作作用于S后产生的目标增量值,选取最小值对应的序对更新S,计算新的A、 V、 CP和U; 重复上述过程直至S不再变化. 该过程称为局部邻域搜索. 其步骤描述如下:
步骤1 对扰动后的解S执行外循环,即先计算S的邻域结构变化后产生的A、 V、 CP和U,循环计数t←0.
步骤2 判断V、 CP和A是否不全为空: 若是,则执行步骤3; 否则,转步骤4.
步骤3 对S执行内循环,即先从{A,V}中随机取一作业πfrom,任取另一作业πto←S-πfrom或从CP中随机取出πto,任取πfrom←U. 然后,选取所有可能的序对(from,to),并评估相应作业对交换操作Swap(S,from,to)、 移位操作Shift(S,from,to)对应的局部最小目标增量值Δtop1和Δto2,选取较小值Δt←min{Δtop1,Δtop2}. t←t+1,转步骤2.
步骤4 取最小增量Δmin←min{Δ1,Δ2,…,Δt}. 若Δmin<0,则S接受Δmin对应的序对操作,转步骤1; 否则,邻域最优解Sb←S,算法停止并返回Sb.
LNS算法由两层循环构成,内循环表示对S执行局部交换、 移位对应的增量评估过程,循环时间复杂度为O(n); 外循环表示S得到改进次数设为c,实际上,算法每次运行时,c值是变化的,故LNS算法复杂度为O(cn).
4 基于局部邻域搜索的量子萤火虫优化(QGSOLNS)算法 4.1 基本萤火虫算法在基本萤火虫算法中,算法的优化机制主要由以下4个参数确定.
1) 亮度: 表示萤火虫的相对荧光亮度,用I(r)表示:

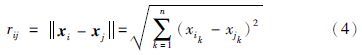

2) 吸引度: 表示萤火虫之间的吸引度,可用β表示,定义为
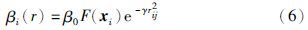
3) 移动: 萤火虫i受到一个更亮的萤火虫j吸引后,按式(7)来确定位置移动方式.
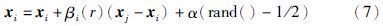
4) 搜索半径: 萤火虫i的搜索半径rd决定了其可感知其它个体的亮度范围,并选择亮度更大的个体组成其邻域集Ni,通过一定的选择算法选取要移动到的个体. 移动完毕,按式(8)更新搜索半径的值:
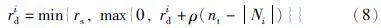
在QGSOLNS中,量子个体q的每个量子位的状态|φ〉的概率幅度用量子角形式表示,即|φ〉=[α,β]T=[cos θ,sin θ]T. 在NWFS问题中,q的每个量子位可代表一个作业,则包含n个作业的q可编码为
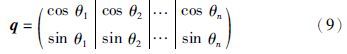
本文采用单链编码方式,即q=(cos θ1,cos θ2,…,cos θn),群体初始化时,量子角θj(j=1,2,…,n)在[0,2π]内随机生成. 量子解码采用变异的LOV(largest-order-value)规则[20]对q的值进行升序排列,并对排序后的值依次搜索其在排序前序列中的位置,得到的位置序列{x1,x2,…,xn}可生成一组作业{Jx1,Jx2,…,Jxn},即解码结果.
4.3 QGSOLNS算法QGSOLNS算法融合了萤火虫算法、 量子进化机制和局部邻域搜索策略,其基本思想是: 先用量子编码方案随机产生一定规模的萤火虫种群,每只萤火虫的位置表示一种调度作业序列; 然后,任取一个体S进行解码,采用ISCH算法[6]进行优化,并对优化结果执行个体重排,以保持生成的新量子编码序列解码结果正确; 个体重排完毕后,根据式(3)~式(5)计算每个个体i的相对荧光亮度,构造相应的邻域集,并采用赌轮法从中选取一个体j,按式(6)和式(7)对i的量子旋转门进行更新; 接着,按式(8)更新其搜索半径值,并对新种群个体进行量子解码及适应度评估,取出群体最优解后执行LNS算法优化,对优化结果再次进行重排,重复上述过程,直至满足停止条件; 最后输出全局最优解. 算法框架如图 4所示.

|
| 图 4 QGSOLNS算法框架 Fig. 4 QGSOLNS algorithm framework |
图 5描述了个体重排过程. 在图 5中,S的量子编码q=(0.564,0.281,0.37,0.009,0.963,0.55),经解码后得到一个作业序列Sold={J4,J2,J3,J6,J1,J5},采用ISCH优化得到一个改进序列Snew={J3,J6,J4,J1,J2,J5},然后对S进行重排. 重排过程是通过移位S的编码序列实现,它由多次移位过程构成,移位次序由量子编码值递增顺序进行,移位次数由序列长度确定,每次移位项的位置和要插入位置分别由Sold和Snew的作业下标决定. 图 5中虚线箭头指示的就是第一次移位过程,可用Shift(q,4,3)表示,其中,4和3分别为S1old和S1new的作业下标. 上述初始序列经过6次移位后,结果为(0.55,0.564,0.009,0.37,0.963,0.28),即S的新编码序列S′.

|
| 图 5 个体重排过程示例 Fig. 5 The example of individual rearrangement process |
QGSOLNS算法步骤描述如下:
步骤1 初始化种群各参数,包括种群大小nps、 最大进化代数g等. 令加工时间矩阵为Pn×m,根据P计算作业开工距离矩阵Dn×n,迭代次数t←0.
步骤2 对种群执行量子编码{S1,S2,…,Snps}←Encoding(),任取一个体并执行ISCH算法以生成较优的初始解S. 最优调度序列S*←S.
步骤3 对S执行量子重排过程S′←Re-Permu(S),S←S′.
步骤4 对每个萤火虫个体Si,搜索其搜索半径rdi内的个体Sj(i,j=1,2,…,nps),然后,按式(4)计算两者的距离rij. 若距离Si的rij处亮度Ii(r)≥I0,则将Sj加入Si的邻域集Ni←{Sj}.
步骤5 对Ni执行赌轮法选择个体Sj←Routte(Ni). 按式(6)和式(7)执行量子旋转门更新Rotate(i,j),按式(8)更新萤火虫Si的搜索半径rdi,然后对Si执行量子解码得(Si)′←Decoding(Si),并计算(Si)′目标函数值f((Si)′),根据f((Si)′)取群体最优解S←min{(S1)′,(S2)′,…,(Snps)′}.
步骤6 执行Sb←LNS(S). 若f(Sb)<f(S*),则(S,S*)←Sb; 否则不更新S和S*.
步骤7 t←t+1. 若t<g,转步骤3; 否则,算法停止并返回S*.
QGSOLNS算法的时间开销主要集中在步骤1、 步骤2和步骤6,由于nps、 g等循环控制参数仿真时设为一个常量,可得时间复杂度分别为O(mn2)、 O(n3)和O(cn),整个算法的复杂度为max{O(mn2),O(n3)}.
5 仿真实验与分析为了验证所提算法的性能,对Fm|nwt|∑Ci问题,采用Taillard[21]110个基准实例测试. 按问题规模将20×5到200×20分为11组,每组10个实例,如: 20×5组包括Ta001-Ta010. 算法仿真采用VC++实现,并在CPU 2.83 GHz、 RAM 2 GB的PC机上运行.
5.1 参数设置参数设置的标准是测试各参数数据以判断算法优化能力是否达到最佳. 经多次实验比较,QGSOLNS算法的各参数值设置如表 1所示.
| 参数名称 | 值 | 说明 |
| g | 500 | 最大进化代数 |
| nps | 100 | 种群规模 |
| γ | 0.6 | 光强吸收系数 |
| α | 0.2 | 步长因子 |
| I0 | 5 | 初始荧光亮度值 |
| β0 | 1.0 | 最大吸引度 |
| ρ | 0.08 | 动态搜索半径更新率 |
| r0 | 4 | 萤火虫个体的初始决策范围 |
| rs | 20 | 萤火虫个体的最大感知范围 |
| nt | 5 | 个体邻域集内包含的萤火虫群数目的阈值 |
表 2给出了LNS算法与2种较优的VNS算法VNS_J[12](记文[12]提出的VNS算法为VNS_J)、 VNS_4[22]进行时间性能比较(单位: s). 为公平起见,3种算法均在同一机器上运行,邻域解的变化采用目标增量法且算法的最大迭代次数相同,依次取50(短期,记为K)、 100(中期,记为M)和500(长期,记为L).
| n×m | VNS_J | VNS_4 | LNS |
| K/M/L | K/M/L | K/M/L | |
| 20×5 | 0/0/0.07 | 0/0.02/0.13 | 0/0/0.03 |
| 20×10 | 0/0.01/0.1 | 0.01/0.02/0.15 | 0/0/0.05 |
| 20×20 | 0/0.01/0.09 | 0.01/0.02/0.16 | 0/0.01/0.05 |
| 50×5 | 0.8/1.5/7.6 | 1.7/3.45/15.88 | 0.05/0.11/0.49 |
| 50×10 | 0.73/1.62/7.95 | 1.74/3.53/16.02 | 0.05/0.13/0.41 |
| 50×20 | 0.75/1.65/8.02 | 1.81/3.64/17.21 | 0.05/0.1/0.45 |
| 100×5 | 2.01/3.98/18.92 | 5.13/11.22/49.8 | 0.2/0.41/1.97 |
| 100×10 | 2.14/4.1/19.25 | 5.05/11.34/49.73 | 0.19/0.38/1.96 |
| 100×20 | 2.07/4.12/19.11 | 5.15/11.3/50.03 | 0.21/0.4/1.95 |
| 200×10 | 14.16/27.93/136.8 | 33.2/58.73/306.4 | 1.74/3.47/17.1 |
| 200×20 | 14.9/28.24/135.76 | 32.05/57.1/301.51 | 1.73/3.46/17.14 |
| 均值 | 3.41/6.65/32.15 | 7.8/14.58/73.37 | 0.38/0.77/3.78 |
由表 2可知,算法时间性能从好到坏依次为LNS、 VNS_J和VNS_4. 对于均值,VNS_J算法的K、 M和L值分别为3.41 s、 6.65 s和32.15 s; VNS_4算法相应分别为7.8 s、 14.58 s和73.37 s; 而LNS只有0.38 s、 0.77 s和3.78 s,远小于VNS_4和VNS_J算法的耗时值. 这说明LNS具有更高的运行效率.
为验证所提算法的性能,将QGSOLNS与目前较优的启发式算法IHA、 群智能算法DGSO、 GA-VNS和DHS进行比较,性能指标采用ARPD(average relative percentage deviation),计算公式如下:
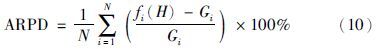
| 问题规模n×m | 算法 | ||||
| IHA | DGSO | GA-VNS | DHS | QGSOLNS | |
| 20×5 | 2.959 | 0.082 | 0 | 0 | 0 |
| 20×10 | 1.812 | 0.071 | 0 | 0 | 0 |
| 20×20 | 0.799 | 0.049 | 0 | 0 | 0 |
| 50×5 | 13.228 | 0.44 | 0 | 0.1 | 0.094 |
| 50×10 | 7.61 | 0.326 | 0.042 | 0.087 | 0.136 |
| 50×20 | 8.775 | 0.338 | 0.064 | 0.139 | 0.135 |
| 100×5 | 17.395 | 0.67 | 0.067 | 0.195 | 0.037 |
| 100×10 | 17.727 | 0.68 | 0.112 | 0.224 | 0.012 |
| 100×20 | 13.142 | 0.526 | 0.125 | 0.313 | 0.008 |
| 200×10 | 21.563 | 0.831 | 0.153 | 0.234 | 0 |
| 200×20 | 19.699 | 0.883 | 0.159 | 0.481 | 0 |
| 均值 | 10.831 | 0.445 | 0.066 | 0.161 | 0.038 |
由表 3可知,QGSOLNS算法对中小规模作业(n=20,50)优化效果较GA-VNS算法、 DHS算法并不明显,但在大规模作业(n=100,200)下,QGSOLNS算法明显优于其他算法. 这是因为在QGSOLNS算法中,一方面采用了目标增量法及局部邻域优化方法,极大地加快了算法迭代速度; 另一方面,引入了量子机制的QGSOLNS算法是一种全局搜索性质的算法,当n值较大时有利于扩大算法的搜索空间并降低种群“早熟”概率. 平均而言,5种算法中,IHA、 DGSO、 GA-VNS和DHS的ARPD值分别为10.831%、 0.445%、 0.066%和0.161%,而QGSOLNS最小,只有0.038%,较前4种算法分别改善了99.65%、 91.46%、 42.42%和76.4%,说明了所提算法的高效性.
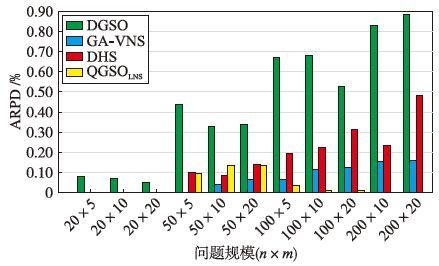
为了能够更直观地进行算法性能对比,将所提算法与上述较优的算法DGSO、 GA-VNS和DHS进行ARPD性能对比,如图 6所示.
|
| 图 6 DGSO、 GA-VNS、 DHS和QGSOLNS的ARPD比较图 Fig. 6 Diagram of ARPD comparison among DGSO,GA-VNS,DHS and QGSOLNS algorithms |
由图 6可知,当n≤50时,所提算法的ARPD值优势并不明显; 而当n>50时,其值明显低于DGSO、 GA-VNS和DHS. 这说明QGSOLNS算法更适合大规模无等待调度.
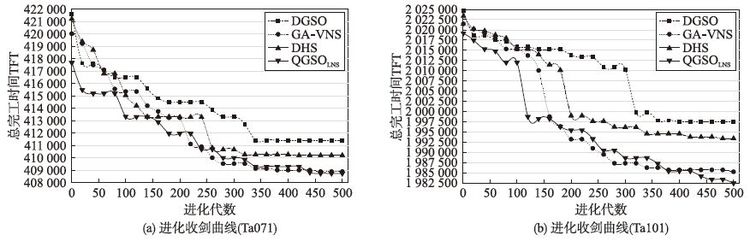
图 7描述了4种算法在Ta071、 Ta101实例下的进化收敛曲线. 由图 7(a)可知,4种算法的收敛速度在开始时大致相同,然而进化到了350代左右,DGSO、 GA-VNS和DHS基本陷于“停滞”,而QGSOLNS由于具有较优的初始解,并利用量子萤火虫混合算法及快速高效的局部邻域搜索策略,最终获得了全局最优解,可以看出QGSOLNS具有更好的全局搜索能力; 图 7(b)的收敛情况则更为明显,说明所提算法在大规模调度下具有更强的优化性能.
|
| 图 7 DGSO、 GA-VNS、 DHS和QGSOLNS算法的进化收敛曲线对比 Fig. 7 Comparison of convergence curves among DGSO,GA-VNS,DHS and QGSOLNS algorithms |
本文提出了一种高效的量子萤火虫优化算法,解决了无等待流水调度最小化总完工时间问题. 通过采用量子优化编码和旋转机制、 快速的目标增量计算及高效的局部邻域搜索方法,极大地加快了算法迭代速度,拓展了算法全局搜索能力. 与目前较优的几种算法在标准测试用例上进行仿真实验比较,结果表明所提算法性能高效,能有效地求解Fm|nwt|∑Ci问题.
| [1] | 张其亮, 陈永生. 求解双向无等待混合流水车间调度问题的粒子群优化算法[J]. 计算机集成制造系统, 2013, 19(10): 2503-2509. Zhang Q L, Chen Y S. Particle swarm optimization algorithm for bi-directional no-wait hybrid flow shop problem[J]. Computer Integrated Manufacturing Systems, 2013, 19(10): 2503-2509. |
| [2] | 潘全科, 赵保华, 屈玉贵. 无等待流水车间调度问题的优化[J]. 计算机学报, 2008, 31(7): 1147-1154. Pan Q K, Zhao B H, Qu Y Q. Heuristics for the no-wait flow shop problem with makespan criterion[J]. Chinese Journal of Computers, 2008, 31(7): 1147-1154. |
| [3] | Rajendran C, Chaudhuri D. Heuristic algorithms for continuous flow-shop problem[J]. Naval Research Logistics, 1990, 37(5): 695-705. |
| [4] | Bertolissi E. Heuristic algorithm for scheduling in the no-wait flow-shop[J]. Journal of Materials Technology, 2000, 107(1): 459-465. |
| [5] | 朱夏, 李小平, 王茜. 基于目标增量的无等待流水调度快速迭代贪婪算法[J]. 计算机学报, 2009, 32(1): 132-141. Zhu X, Li X P, Wang Q. Objective increment based iterative greedy heuristic for no-wait flowshops with total flowtime minimization[J]. Chinese Journal of Computers, 2009, 32(1): 132-141. |
| [6] | 李亚志, 朱夏. 基于插入-分段的无等待流水作业调度复合启发式算法[J]. 东南大学学报: 自然科学版, 2013, 43(3): 483-488. Li Y Z, Zhu X. Insertion-segment based composite heuristic algorithm for no-wait flow shop scheduling problems[J]. Journal of Southeast University: Natural Science Edition, 2013, 43(3): 483-488. |
| [7] | Laha D, Sapkal S U. An improved heuristic to minimize total flow time for scheduling in the m-machine no-wait flow shop[J]. Computers & Industrial Engineering, 2014, 67: 36-43. |
| [8] | Aldowaisan T, Allahverdi A. New heuristics for m-machine no-wait flowshop to minimize total completion time[J]. Omega, 2004, 32(5): 345-352. |
| [9] | Framinan J M, Nageno M S, Moccellin J V. An efficient heuristic for total flowtime minimization in no-wait flowshops[J]. International Journal of Advanced Manufacturing Technology, 2010, 46: 1049-1057. |
| [10] | Pan Q K, Tasgetiren M F, Liang Y C. A discrete particle swarm optimization algorithm for the no-wait flowshop scheduling problem[J]. Computers & Operations Research, 2008, 35(9): 2807-2839. |
| [11] | Gao K Z, Pan Q K, Li J Q. Discrete harmony search algorithm for the no-wait flow shop scheduling problem with total flow time criterion[J]. International Journal of Advanced Manufacturing Technology, 2011, 56: 683-692. |
| [12] | Jarboui B, Eddaly M, Siarry P. A hybrid genetic algorithm for solving no-wait flowshop scheduling problems[J]. International Journal of Advanced Manufacturing Technology, 2011, 54: 1129-1143. |
| [13] | 周永权, 黄正新, 刘洪霞. 求解TSP问题的离散型萤火虫群优化算法[J]. 电子学报, 2012, 40(6): 1164-1170. Zhou Y Q, Huang Z X, Liu H X. Discrete glowworm swarm optimization algorithm for TSP problem[J]. Acta Electronica Sinica, 2012, 40(6): 1164-1170. |
| [14] | 曾冰, 李明富, 张翼. 基于改进萤火虫算法的装配序列规划方法[J]. 计算机集成制造系统, 2014, 20(4): 799-806. Zeng B, Li M F, Zhang Y. Assembly sequence planning based on improved firefly algorithm[J]. Computer Integrated Manufacturing Systems, 2014, 20(4): 799-806. |
| [15] | 杜鹏桢, 唐振民, 陆建峰, 等. 不确定环境下基于改进萤火虫算法的地面自主车辆全局路径规划方法[J]. 电子学报, 2014, 42(3): 616-624. Du P Z, Tang Z M, Lu J F, et al. Global path planning for ALV based on improved glowworm optimization under uncertain environment[J]. Acta Electronica Sinica, 2014, 42(3): 616-624. |
| [16] | 张军丽, 周永权. 人工萤火虫与差分进化混合优化算法[J]. 信息与控制, 2011, 40(5): 608-613. Zhang J L, Zhou Y Q. A hybrid optimization algorithm based on artificial glowworm swarm and differential evolution[J]. Information and Control, 2011, 40(5): 608-613. |
| [17] | Karthikeyan S, Asokan P, Nickolas S. A hybrid discrete firefly algorithm for multi-objective flexible job shop scheduling problem with limited resource constraints[J]. International Journal of Advanced Manufacturing Technology, 2014, 72: 1567-1579. |
| [18] | 王凌. 量子进化算法研究进展[J]. 控制与决策, 2008, 23(12): 1321-1326. Wang L. Advances in quantum-inspired evolutionary algorithms[J]. Control and Decision, 2008, 23(12): 1321-1326. |
| [19] | 宋存利. 生产调度问题及其智能优化算法研究[D]. 大连: 大连理工大学, 2011. Song C L. Research on production scheduling problem and intelligent optimization algorithm[D]. Dalian: Dalian University of Technology, 2011. |
| [20] | Qian B, Wang L, Hu R. A DE-based approach to no-wait flow-shop scheduling[J]. Computers & Industrial Engineering, 2009, 57: 787-805. |
| [21] | Taillard E. Benchmarks for basic scheduling programs[J]. European Journal of Operational Research, 1993, 64(2): 278-285. |
| [22] | Costa W E, Goldbarg M C, Goldbarg E G. New VNS heuristic for total flowtime flowshop scheduling problem[J]. Expert Systems with Applications, 2012, 39(9): 8149-8161. |



