2. 湖南工学院信号与信息处理重点实验室, 湖南 衡阳 421002
2. Key Laboratory of Signal & Information Processing, Hunan Institute of Technology, Hengyang 421002, China
1 引言
混沌控制技术被广泛应用于非线性电路、 流体力学、 神经网络等研究领域，其在工程和理论上的研究价值引起了越来越多研究学者的关注，成为非线性科学研究的热点之一.
近年来，分数阶系统逐渐成为国际上的研究热点，对分数阶系统的混沌特性及其控制的研究已成为混沌学领域一个新的研究课题[1]. 许喆等人基于李亚普诺夫方程的系统稳定性理论，实现了分数阶混沌系统的控制[2]； 赵小国等人实现了基于径向基神经网络的分数阶混沌系统的控制[3]； 阎晓妹等人实现了基于最小二乘支持向量机的分数阶混沌系统的控制[4]. 但是他们都没有考虑在不影响被研究系统混沌运动和全局稳定的前提下，如何将分数阶系统从不稳定状态控制到稳定状态，而在实际工程应用中尤其是金融系统的控制中不可避免地会遇到这类情况，所以有必要研究在不影响被研究系统混沌运动和全局稳定的前提下分数阶混沌系统的控制问题.
本文将一种有效的混沌控制方法——参数切换法——应用于分数阶系统. 以分数阶洛伦兹系统为例，该方法在一个相对较短的时间周期，通过在一组可供选择的数值内切换系统的一个可控参数来实现的，并结合Grünwald—Letnikov(GL)方案，合成了该系统的稳定吸引子，达到了混沌控制的目的. 仿真结果表明了该方法的有效性.
2 分数阶洛伦兹混沌系统的GL离散化处理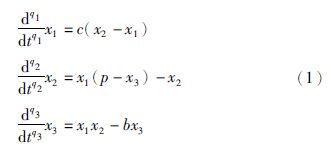
式(1)可改写为如下的广义初值问题(IVP)[7]：
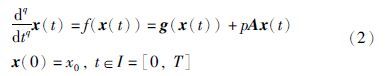
其中，x： I→R3，g： R3→R3是一个连续的非线性函数，A是一个3×3的实常数矩阵，p是一个可调的实参数，通过切换它的值来实现混沌控制.
式(2)广义初值问题可以用来描述一大类常见的分数阶及整数阶动力学系统，例如Rössler系统[8]、 Chen系统[9]、 Chua系统[10, 11]等.
对于式(1)，有
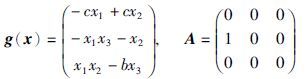
当q=1，式(2)对应经典的一阶初值问题，它可以通过标准方法数值求解，如龙格库塔(Runge-Kutta)法. 另一方面，对于q∈(0，1)，式(2)对应一个分数阶初值问题，通过分数阶微分方程表示.
在本文中，使用Caputo定义的分数微分算子dq/dtq，起始点为t0=0，即[12, 13, 14]：
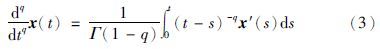
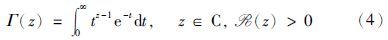
引入非整数阶微分的另一种方法是Grünwald-Letnikov (GL)算子[15]
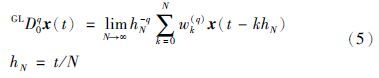
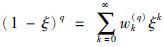展开式的系数，可以通过以下方式计算[15]：
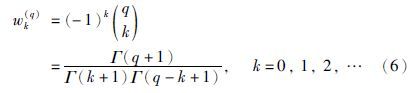
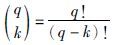
GL的离散化方案可以用来求解Caputo形式的分数阶微分方程，形式如下[15]：
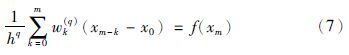
为了数值实现式(2)初值问题的分数阶洛伦兹系统模型的参数切换算法，可以使用GL离散化方案. 联系式(1)，可以得到以下等式：
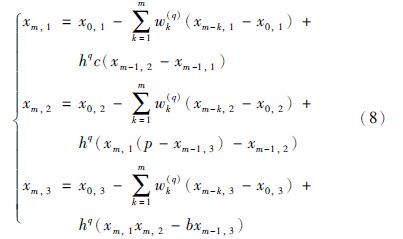
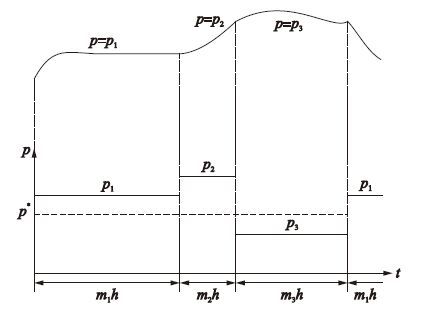
假定在区间I上从给定的初值x0对系统进行数值积分，在一组可供选择的实数pN=｛p1，p2，…，pN｝(N>1)内周期地切换p值以实现参数切换算法[16]. 首先把区间I划分为长度为h倍数的子区间，其中h>0，表示步长. 图 1中，设置第1个子时间区间p=p1的长度为m1h，第2个子时间区间p=p2的长度为m2h，…，直到第N个子时间区间p=pN的长度为mNh(图 1中，N=3). 权重mi，i=1，2，…，N为正整数. N个区间重复，直到时间区间I被完全覆盖.
|
| 图 1 参数切换算法示意图 Fig. 1 Parameter switching algorithm |
对于一个固定的h，切换方案可以表示为
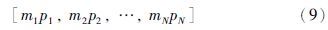
例如，[2p1，1p2]为用p集成的全局初值问题p1，p1，p2，p1，p1，p2，…，每一个集成步骤时间为h.
其次令p*表示在式(10)方案下的平均值，可以通过式(10)计算[17]：
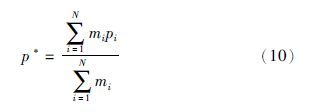
在切换方案(9)下获得的解逼近p=p*时生成的解.
3.2 参数切换算法收敛性证明考虑式(2)初值问题，当q=1，假设它的解有且仅有一个标准条件(即利普希茨连续)，于是有：
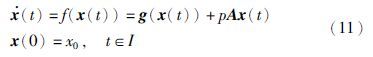
基于参数切换算法，当p为周期性变化时，等式(11)可以转换为
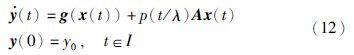
其中，y∈R3，λ是一个很小的正实数.
参数p可以被看作一个分段地以常数T0为周期的周期函数，它的平均值p*可以通过式(13)计算：
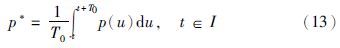
考虑式(11)的模型，用p*替换p，即
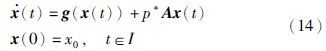
基于平均理论[18, 19]，以相同的初始值x0=y0为起点，式(12)和式(14)的解对于某一常数α，当λ是足够小时，相差不到αλ2，证明见参考文[20].
4 基于参数切换的混沌控制对属于某一个吸引域的每一个初始状态x0，可以通过龙格库塔(Runge-Kutta)或GL方案来求得式(2)分数阶系统的唯一解. 忽略一段足够长的过渡时间周期，它的解将趋近所研究的吸引域的一个特定吸引子. 不失一般性，一个吸引子被理解为从某一个初始状态x0开始的解的数值逼近，它表征为瞬变系统的渐进动力学.
现在，考虑pN=｛p1，p2，…，pN｝，获得的与pN唯一对应的吸引子集合为AN=｛Ap1，Ap2，…，ApN｝，在pN与AN之间存在单调双向映射. 因此，记pmin和pmax为pN的最小和最大值，有实数区间(pmin，pmax)对应吸引子区间(Apmin，Apmax). 把使用参数切换算法获得的合成吸引子计作A0，用p*替换p时获得的平均吸引子计作A*. 基于参数切换算法的收敛性[12, 20]，可以证明对于给定的pN和权重m1，m2，…，mN，N>1，合成的吸引子A0很好地吻合平均吸引子A*，且此处合成的稳定吸引子与平均吸引子的豪斯多夫距离以10-4阶出现.
p*值是由(10)式给定的一个凸组合，pi，i=1，2，…，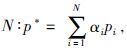
其中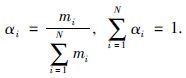
因此，给定权重为m1，m2，…，mN的pN，p*落在实区间(pmin，pmax)内. 此外，A0同样地落在了区间(Apmin，Apmax). 这种属性在本质上体现了参数切换算法具有很强的鲁棒性.
由于p*的凸性，参数切换算法在方案(9)为周期或随机时都可用. 例如，假设目标平均值为p*，pi的权重通过mi给定，pi以概率mi在模型中出现. 于是，在一个足够长的时间周期有：
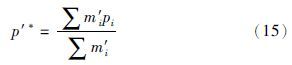
其中，m′i代表每一个pi发生的次数，有p′*≈p*.
如上所述，参数切换算法能够逼近式(2)建模的任意系统的每一个吸引子.
因此，参数切换算法可以作为混沌控制技术使用. 相比其它的混沌控制方法，很容易发现参数切换算法并没有改变合成吸引子A0的原始属性，在实际的混沌控制中，这一特性是非常重要而有价值的.
5 仿真结果现在，对式(2)初值问题应用上述参数切换算法来获得式(1)系统分数阶稳定状态. 设定参数为b=0.1，c=1，阶数qi=0.99(i=1，2，3)，初始值(x0，1，x0，2，x0，3)=(0.1，0.001，0.001). 为了得到数值解，通过式(12)的GL方法在初值问题下进行合成. 积分时间区间I=[0, 100]，积分步长h=0.05. 通过比较吸引子A0和A*来验证参数切换算法的有效性. 通过画相位图发现，最大的稳定窗口中心在p=17，被调节的值属于临近的混沌窗口.
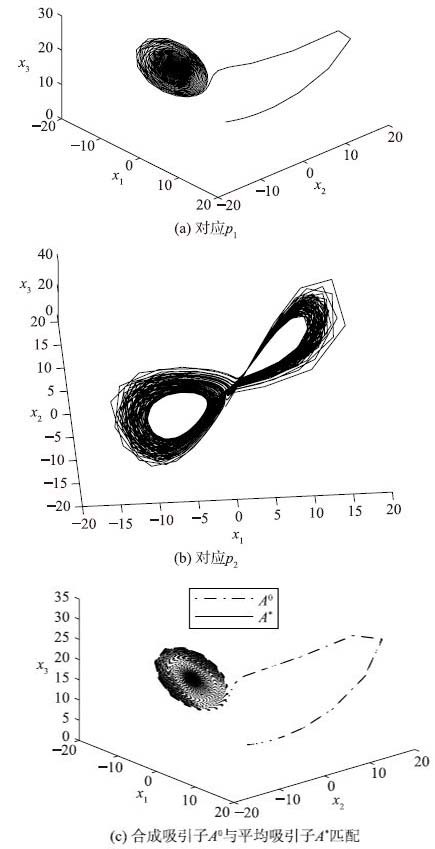
假设需得到一个p*=17对应的稳定运动状态，参数切换方案为[m1p1，m2p2]，其中p1=16.5，p2=17.5，设定权重为m1=m2=1，p1=16.5的动力学行为如图 2(a)所示； p2=17.5的运动状态为一个混沌吸引子，如图 2(b)所示. 通过参数切换算法可获得合成吸引子A0，与p*=17对应的平均吸引子A*很好的匹配，如图 2(c)所示. 甚至
|
| 图 2 参数切换方案[1p1，1p2]，其中p1=16.5，p2=17.5，p*=17 Fig. 2 Parameter switching algorithm applied to the values [1p1，1p2]，p1=16.5，p2=17.5，p*=17 |
当p1和p2有一个不是来自混沌窗口，参数切换算法仍然可以像混沌控制方案那样工作，得到一个稳定的吸引子A0.
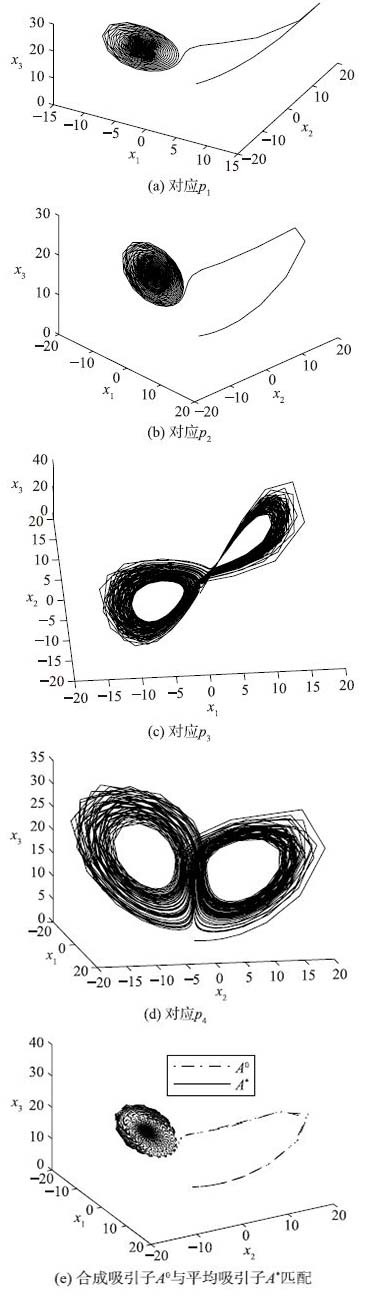
当转换值pN的个数N>2仍然可以合成同样的吸引子. 例如，考虑方案[m1p1，m2p2，m3p3，m4p4]，p4=｛16，16.5，17.5，18｝，m1=m2=m3=m4=1. 再一次得到p*=17(如图 3(e)).
|
| 图 3 参数切换方案[1p1，1p2，1p3，1p4]，其中p1=16，p2=16.5，p3=17.5，p4=18，p*=17 Fig. 3 parameter switching algorithm applied to the values [1p1，1p2，1p3，1p4]，p1=16，p2=16.5，p3=17.5，p4=18，p*=17 |
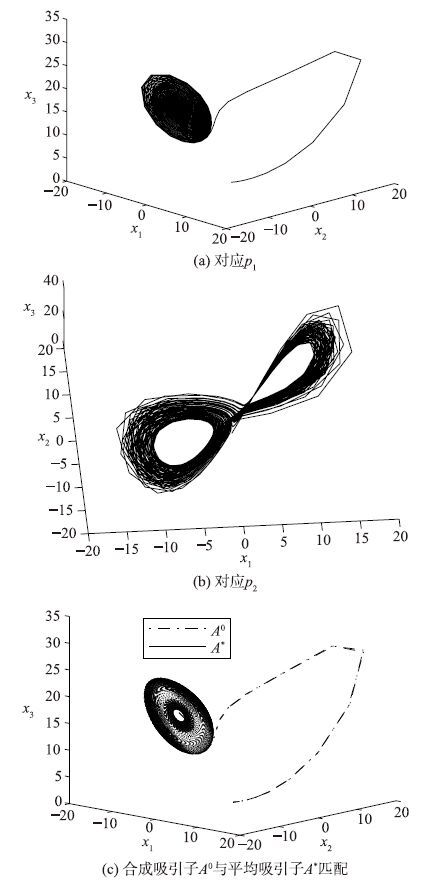
当切换方案[m1p1，m2p2]中m>1同样可以合成稳定吸引子，例如，[1p1，2p2]，p1=17(如图 4(a)所示)，p2=17.5(如图 4(b)所示)，对应p*=17.33，合成的吸引子A0与平均吸引子A*很好的匹配(如图 4(c)所示).
|
| 图 4 参数切换方案[1p1，2p2]，其中p1=17，p2=17.5，p*=17.33 Fig. 4 parameter switching algorithm applied to the values [1p1，2p2]，p1=17，p2=17.5，p*=17.33 |
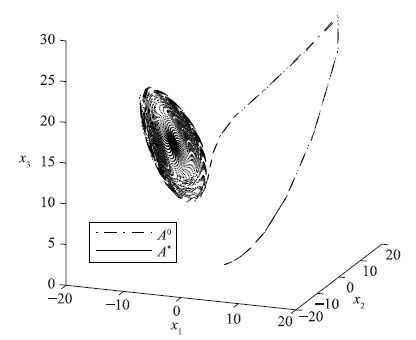
参数切换方案也可以以随机的方式应用. 例如，考虑以pi，i∈｛1，2｝为转换秩序，P2=｛16，17.5｝，每一步的积分为随机的，在时间区间I=[0, 100]，步长为h=0.05，仿真结果如图 5，联系(17)式计算给出p*=16.75. 需要申明的是，由于切换方案的随机性，使用了一个更小的h值可以使合成吸引子和平均吸引子更好地匹配. 增长时间区间I也会得到一个更好的匹配结果，因为那样能够使式(17)的右边更加趋近p*的值.
|
| 图 5 随机参数切换方案P2=｛16，17.5｝ Fig. 5 Random parameter switching algorithm applied to the values P2=｛16，17.5｝ |
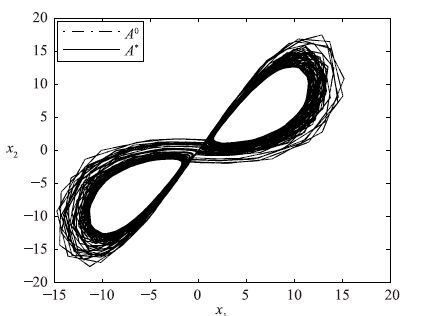
首先，讨论分数阶洛伦兹混沌系统的初始值对参数切换算法的影响. 图 2的初始值为(x0，1，x0，2，x0，3)=(0.1，0.001，0.001)，图 6的初始值为(x0，1，x0，2，x0，3)=(1，1，2)，分数阶数为qi=0.99(i=1，2，3)，切换的参数为p1=16.5，p2=17.5，平均值为p*=17，合成吸引子(A0)对应的x1-x2相图与平均吸引子(A*)对应的x1-x2相图匹配，故参数切换算法的混沌控制不受初始值的影响.
|
| 图 6 初始值不同时的相图匹配结果 Fig. 6 Matching results of phase diagram from different original values |
其次，讨论分数阶洛伦兹混沌系统的阶数对参数切换算法的影响. 在初始值为(x0，1，x0，2，x0，3)=(0.1，0.001，0.001)，参数切换值为p1=16.5，p2=17.5，平均值为p*=17的前提下，可以实现参数切换的分数阶混沌系统的阶数如表 1所示. 只要在表 1所示的有效范围内，均可以实现参数切换算法对分数阶混沌系统的控制.
| q2=q3=0.99 | q1≥0.63 |
| q1=q2=0.99 | q3≥0.29 |
| q1=q3=0.99 | q2≥0.64 |
最后，讨论分数阶洛仑兹系统的参数. 如式(1)所示，有p、 b、 c三个系统参数，固定b、 c两个参数，分数阶数为qi=0.99(i=1，2，3). 切换参数p≥17.32时分数阶洛仑兹系统表现为混沌吸引子，对应图 2(b)、 图 3(c)和图 3(d)、 图 4(b). 切换参数16≤p≤17.31时分数阶洛仑兹系统表现为稳态环面或稳态点，对应图 2(a)、 图 3(a)和图 3(b)、 图 4(a). 由图 2～图 4可以看出，通过参数切换算法，可以实现混沌吸引子+稳定吸引子=稳定吸引子的控制.
7 结束语本文将一种新的分数阶系统混沌控制方法——参数切换法——应用于分数阶混沌系统中，该方法通过在一定的范围内切换系统的控制参数可以使系统从混沌状态转换为稳定状态，达到混沌控制的目的. 仿真结果表明该方法合成的稳定吸引子与平均吸引子达到了很好的匹配.
数值证明，从任意一组转换参数值开始，在式(1)分数阶情况下使用参数转换算法都可以获得一个稳定的周期. 通过选择一组合适的转换值，该算法可以很方便用来获取混沌吸引子，产生的混沌吸引子能够很好地吻合全局吸引子. 故参数切换算法主要优点是，它不影响全局稳定和被研究系统的混沌运动. 相反，很多其它的混沌控制和反控制技术对全局混沌系统的稳定变量或参数表现出扰动. 从这点看，参数切换算法表现得更像一个无损算法. 参数切换算法另一个优点是，它可以对某些显然是由非常复杂的动态切换引起的某些稳态或混沌运动在本质上做出很好的解释.
| [1] | 王跃钢, 文超斌, 杨家胜. 基于无模型方法的混沌系统自适应控制[J]. 物理学报, 2013, 62(10): 100504-1-7. Wang Y G, Wen C B, Yang J S. Adaptive control of chaotic systems based on model free method[J]. Acta Physica Sinica, 2013, 62(10): 100504-1-7. |
| [2] | 许喆, 刘崇新, 杨韬. 基于Lyapunov方程的分数阶新混沌系统的控制[J]. 物理学报, 2010, 59(3): 1521-1531. Xu Z, Liu C X, Yang T. Controlling fractional-order new chaotic system based on Lyapunov equation[J]. Acta Physica Sinica, 2010, 59(3): 1521-1531. |
| [3] | 赵小国, 杜琦, 阎晓妹. 基于径向基神经网络的分数阶混沌系统控制[J]. 信息与控制, 2010, 39(2): 142-146. Zhao X G, Du Q, Yan X M. Control of fractional order chaotic systems via RBF neural network[J]. Information and Control, 2010, 39(2): 142-146. |
| [4] | 阎晓妹, 刘丁. 基于最小二乘支持向量机的分数阶混沌系统控制[J]. 物理学报, 2010, 59(5): 3043-3048. Yan X M, Liu D. Control of fractional order chaotic system based on least square support vector machines[J]. Acta Physica Sinica, 2010, 59(5): 3043-3048. |
| [5] | 贾红艳, 陈增强, 薛薇. 分数阶Lorenz系统的分析及电路实现[J]. 物理学报, 2013, 62(14): 140503-1-7. Jia H Y, Chen Z Q, Xue W. Analysis and circuit implementation for the fractional-order Lorenz system[J]. Acta Physica Sinica, 2013, 62(14): 140503-1-7. |
| [6] | 戴朱祥, 吴庆庆, 李涛. 分数阶Lorenz混沌系统的同步控制[J]. 计算机仿真, 2015, 32(6): 314-319. Dai Z X, Wu Q Q, Li T. Synchronization control of fractional-order lorenz chaotic systems[J]. Computer Simulation, 2015, 32(6): 314-319. |
| [7] | Yu M, Wallace K S T, Danca, M F. An averaging model for chaotic system with periodic time-varying parameter[J]. Applied Mathematics and Computation, 2010, 217(1): 355-362. |
| [8] | Leonov G A, Alexeeva T A. Lyapunov functions in estimates of attractor dimensions for generalized Rssler systems[J]. Doklady Mathematics, 2015, 91(1): 5-8. |
| [9] | 李睿, 张广军, 姚宏, 等. 参数不确定的分数阶混沌系统广义错位延时投影同步[J]. 物理学报, 2014, 63(23): 230501-1-7. Li R, Zhang G J, Yao H, et al. Generalized dislocated lag projective synchronization of fractional chaotic systems with fully uncertain parameters[J]. Acta Physica Sinica, 2014, 63(23): 230501-1-7. |
| [10] | Chen M, Li M Y, Yu Q, et al. Dynamics of self-excited attractors and hidden attractors in generalized memristor-based Chua's circuit[J]. Nonlinear Dynamical, 2015, 81(1): 215-226. |
| [11] | Lin T C, Huang F Y, Du Z B, et al. Synchronization of fuzzy modeling chaotic time delay memristor-based Chua's circuits with application to secure communication[J]. International Journal of Fuzzy Systems, 2015, 17(2): 206-214. |
| [12] | Kilbas A A, Srivastava H M, Trujillo J J. Theory and application of fractional differential equations[M]. Amsterdam, Holland: Elsevier, 2006. |
| [13] | Petráš I. Fractional-order nonlinear systems: Modeling, analysis and simulation[M]. Beijing: Higher Education Press, 2011. |
| [14] | Hadi D, Dumitru B, Jalil S. Stability analysis of Caputo fractional-order nonlinear systems revisited[J]. Nonlinear Dynamical, 2012, 67(4): 2433-2439. |
| [15] | Scherer R, Kalla S L, Tang Y, et al. The Grünwald-Letnikov method for fractional differential equations[J]. Computers & Mathematics with Applications, 2011, 62(3): 902-917. |
| [16] | Danca M F. Random parameter-switching synthesis of a class of hyperbolic attractors[J]. Chaos, 2008, 18(033111): 1-9. |
| [17] | Danca M F, Romera M, Pastor G F. Montoya, finding attractors of continuous-time systems by parameter switching[J]. Nonlinear Dynamics, 2012, 67(4): 2317-2342. |
| [18] | Sanders J A, Verhulst F. Averaging methods in nonlinear dynamical systems[M]. Berlin, Germany: Springer, 1985. |
| [19] | Sana P A, Saurabh K A, Subir D. Stability analysis of fractional-order generalized chaotic susceptible-infected-recovered epidemic model and its synchronization using active control method[J]. Pramana-Journal of physics, 2015, 84(1): 23-32. |
| [20] | Abd-Elouahab M S, Hamri N E, Wang J. Chaos control of a fractional-order financial system[J]. Mathematical Problems in Engineering, 2010(2010): 1-19. |