2. 东北大学信息科学与工程学院, 辽宁 沈阳 110819 ;
3. 沈阳工业大学信息科学与工程学院, 辽宁 沈阳 110870
2. School of Information Science and Engineering, Northeastern University, Shenyang 110819, China ;
3. College of Information Science and Engineering, Shenyang University of Technology, Shenyang 110870, China
1 引言
马尔可夫跳变系统(MJS)最早由Krasovskii等人于20世纪60年代提出的[1],是按照一定的随机切换规则在一组子系统之间进行切换的混杂系统,作为一类特殊的混杂系统,马尔可夫跳变系统能够更好地描述实际控制过程和系统,在过去的几十年中一直是研究的焦点. 例如,在经济系统[2]、 网络控制系统[3]、 工业系统[4]、 故障检测系统[5]等,并已广泛应用于交通系统、 制造系统和电力系统等领域. 注意到较多关于随机马尔可夫跳变系统的研究成果是在假设转移概率完全已知的条件下建立的[6-7].
然而,由于各种实际复杂因素,MJS中转移概率的全部信息可能难以得到或者获取代价很高[8],转移概率数值并非完全已知. 例如,网络控制系统中的丢包和延迟,获取全部转移概率将会付出较大成本. 目前,已有部分学者从事转移概率部分未知的相关研究,取得一些研究成果,如文[9-13].
另一方面,时滞出现在大多数工程领域,将会产生较差性能,甚至导致控制系统的不稳定. 对于带有时滞的马尔可夫跳变系统的研究已经成为热点,包括稳定性[14]、 反馈设计[15]、 滤波器设计[16]、 观测器设计[17]. 然而,转移概率部分未知带有随机时变时滞的MJS研究较少[18-20]. 现在,在实际应用中,系统常常受到各种随机因素的干扰,从而随机系统的研究得到了广泛关注,确定性系统中的许多重要结果已推广应用于随机系统. 但是,目前研究的MJS子系统大多为确定性系统,有关子系统为随机系统的MJS的研究尚不多见,相关最新研究进展参见文[21-23]. 针对转移概率部分未知带有随机时变时滞的MJS鲁棒H∞控制研究,目前还待于进一步深入的研究讨论.
2 研究对象与系统描述考虑如下随机马尔可夫切换系统:
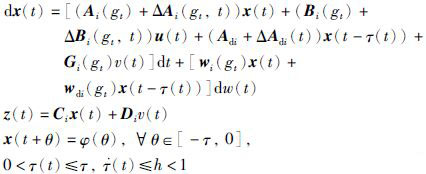
|
(1) |
其中,x(t)∈Rn是状态向量; v(t)∈L2n[0,+∞)是外部扰动信号(具有能量有界,范数可积); w(t)是标准维纳过程; z(t)∈Rl是测量输出; Ai,Bi,Adi,Ci,Di,Gi,wi,wdi是已知的具有适当维数的实常数矩阵; ΔAi(t),ΔBi(t),ΔAdi(t)是未知矩阵,表示时变不确定参数,范数有界的不确定性. 在本文中假设其具有如下形式:
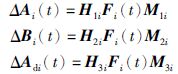
|
其中,H1i,M1i,H2i,M2i,H3i,M3i是已知的适当维数的实常数矩阵,Fi(t)是未知的时变实矩阵,且满足FiT(t)Fi(t)≤I.
gt为有限集S={1,2,…,N}中取值的连续马尔可夫过程. 从t时刻模态i到t+Δt时刻模态j的转移概率:
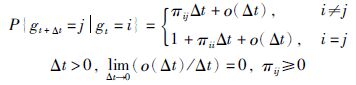
|
当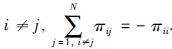
转移概率是建立在部分未知情况下的,意味着转移概矩阵Π=(πij)中有一些元素是部分未知的. 对于∀i∈S,Si表示为Si=Ski+Suki,

|
如果Si≠∅,可以描述为Ski={k1i,k2i,…,kmi},1≤m≤N. 其中kmi∈S代表矩阵Π第i行中序号为kmi的第m个已知元素.
本文构造状态反馈控制器:
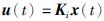
|
(2) |
其中,Ki是状态反馈控制增益.
引理 1 初始状态x0∈Rn与初始模态r0∈M有下面不等式成立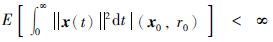
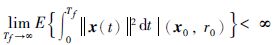
定理 1 转移概率部分未知的系统(3)是随机稳定的,
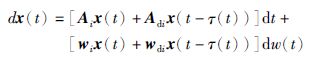
|
(3) |
如果存在正定对称矩阵Pi∈Rn×n,Q1i∈Rn×n,Q1∈Rn×n,Q2i∈Rn×n,Q2∈Rn×n以及对称矩阵R1i∈Rn×n,R2i∈Rn×n,R3i∈Rn×n,对于∀i∈S,使得下式成立
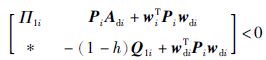
|
(4) |
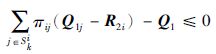
|
(5) |
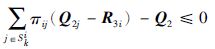
|
(6) |
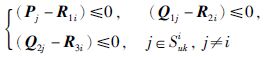
|
(7) |
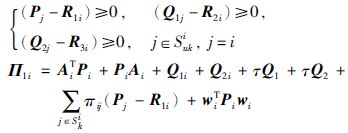
|
(8) |
证明 选择李亚普诺夫函数
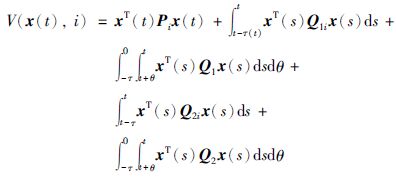
|
(9) |
其中,Pi>0,Q1i>0,Q2i>0,Q1>0,Q2>0.
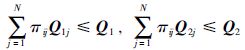
|
(10) |
由无穷小算子定义可得,
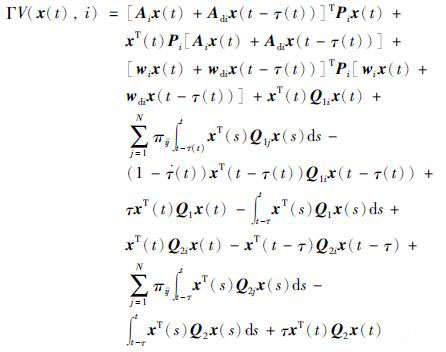
|
(11) |
考虑到πij≥0,(i≠j)由式(10)可得,
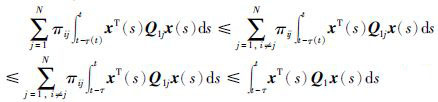
|
(12) |
同理可得,
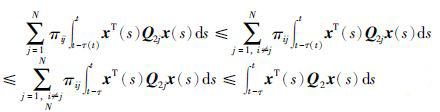
|
(13) |
由于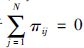
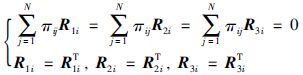
|
(14) |
由于xT(t-τ)Q2ix(t-τ)>0,结合式(9)~式(14)可得,
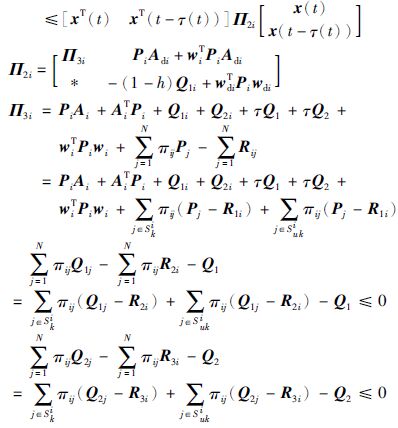
|
(15) |
对于∀j∈Suki,当i∈Ski时,存在正定对称矩阵Pi∈Rn×n,Q∈Rn×n,对称矩阵Ri∈Rn×n,由条件
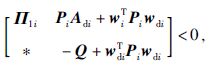
|
(16) |
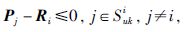
|
(17) |
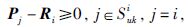
|
(18) |
以及πij≥0(∀i,j∈S,i≠j)可得到ΓV(x(t),i)<0.
另一方面,对于∀ j∈Suki,当i∈Suki时,由条件(16)~(18)和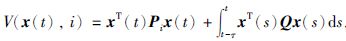
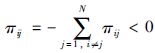
所以,有式(19):
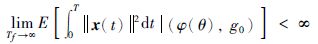
|
(19) |
证明完毕.
4 控制器设计定理 2 转移概率部分未知的闭环系统(1)如下:
系统是鲁棒随机稳定的,并且具有H∞性能γ,如果存在正定对称矩阵Xi∈Rn×n,U1ij∈Rn×n,U2ij∈Rn×n,U1i∈Rn×n,U2i∈Rn×n以及对称矩阵V1i∈Rn×n,V2i∈Rn×n,V3i∈Rn×n,正常数γ,ε1i,ε2i,ε3i,对于∀i∈S,使得下式(20)~(24)成立
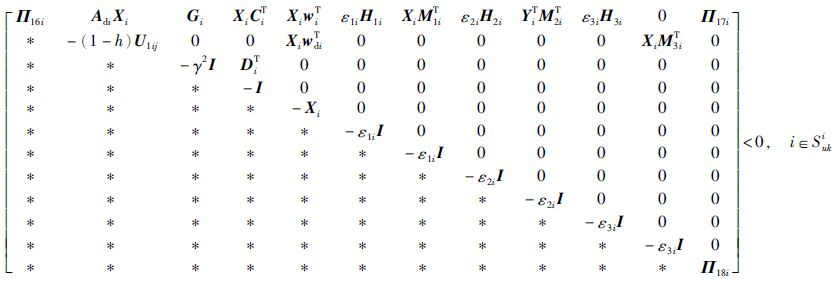
|
(21) |
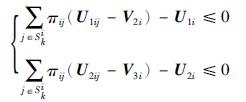
|
(22) |
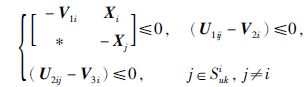
|
(23) |
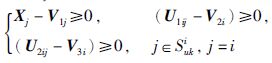
|
(24) |
其中,

|
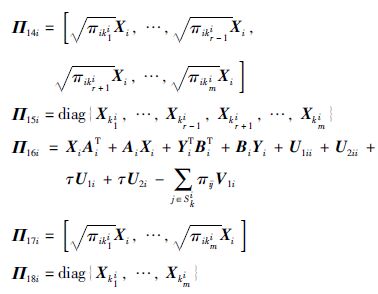
|
控制器增益矩阵为Ki=YiX-1i.
证明
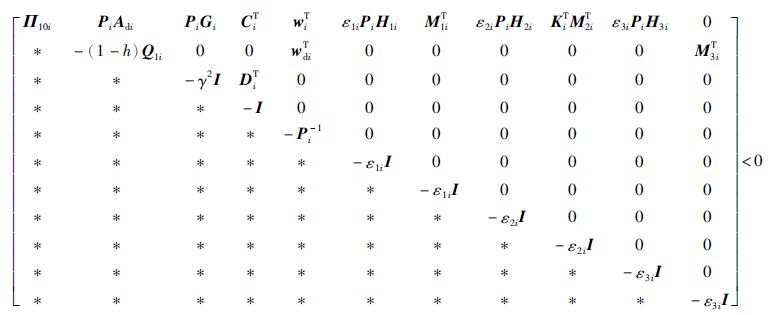
|
(25) |
其中,
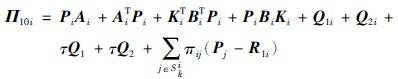
|
注 1 上述结果为系统的鲁棒H∞性能分析时所得.对式(25)分别左乘右乘
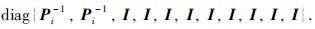
|
令
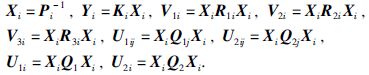
|
可以得到下式
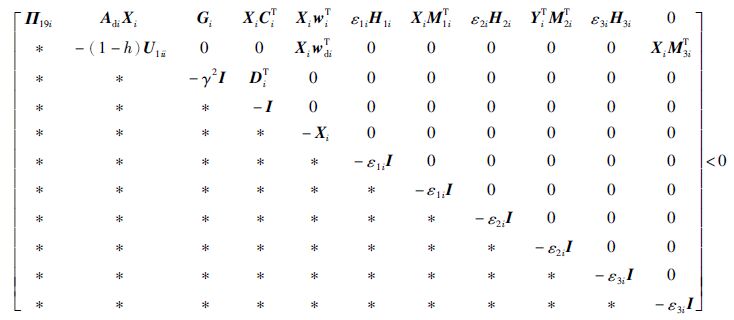
|
(26) |
其中,
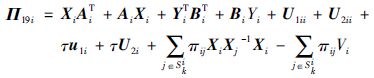
|
由于πij<0,不等式(26)分别讨论如下:
(1) 对于i∈Ski,应用Schur补引理,不等式(26)等价于式(20).
(2) 对于i∉Ski,应用Schur补引理,不等式(26)等价于式(21).
对式(5)和式(6),分别左乘右乘Xi,则有(22)式成立.
对式(7),分别左乘右乘Xi,则有式(23)成立.
对式(8),分别左乘右乘Xi,则有式(24)成立.
证明完毕.
5 仿真举例考虑二维四模态的马尔可夫跳跃系统,其参数为
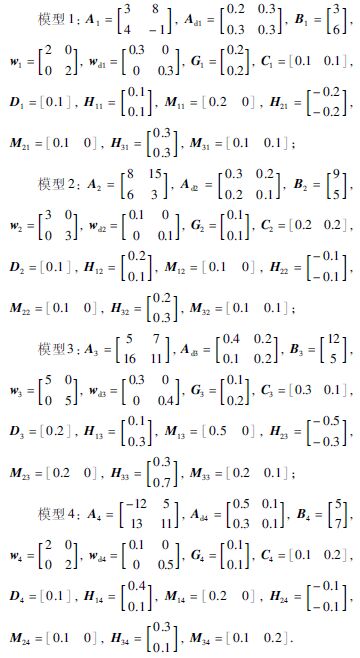
|
通过求解可得H∞性能指标: γ=2.89,控制器增益:
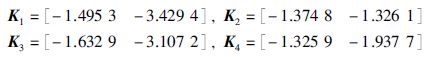
|
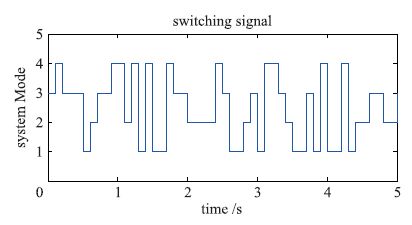
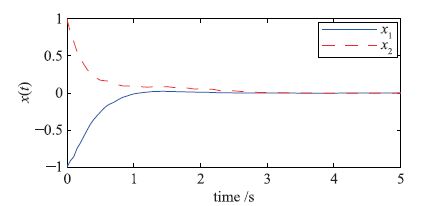
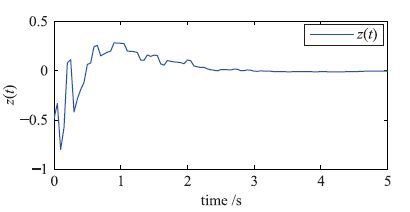
图 1给出了系统的模态,即为此系统对应的马尔可夫切换信号; 图 2给出了系统在t=0到t=5 s时间内的状态轨迹曲线; 图 3给出了系统在t=0到t=5 s时间内的控制输出轨迹曲线. 证明了所设计的鲁棒H∞状态反馈控制器是有效性的.
|
| 图 1 系统模态 Figure 1 System mode |
|
| 图 2 系统状态轨迹 Figure 2 System state trajectories |
|
| 图 3 系统控制输出轨迹 Figure 3 System trajectories of control output |
本文针对转移概率部分未知的随机时变时滞马尔可夫跳变系统,采用线性矩阵不等式,给出系统随机稳定的充分性条件以及鲁棒H∞状态反馈控制器的设计. 最后,数值仿真验证本方法的正确性和有效性.
| [1] | Krasovskii N N, Lidskii E A. Analytical design of controllers in systems with random attributes, Parts Ⅰ-Ⅲ[J]. Automation and Remote Control , 1961, 22 (1/2/3) : 1021–1025. |
| [2] | Chen W H, Xu J X, Guan Z H. Guaranteed cost control for uncertain Markovian jump systems with mode-dependent time-delays[J]. IEEE Transactions on Automatic Control , 2003, 48 (12) : 2270–2277. DOI:10.1109/TAC.2003.820165 |
| [3] | Song Y, Xie J X, Fei M R, et al. Mean square exponential stabilization of networked control systems with Markovian packet dropouts[J]. Transactions of the Institute of Measurement and Control , 2013, 35 (1) : 75–82. DOI:10.1177/0142331211407787 |
| [4] | Shen L J, Buscher U. Solving the serial batching problem in job shop manufacturing systems[J]. European Journal of Operational Research , 2012, 221 (1) : 14–26. DOI:10.1016/j.ejor.2012.03.001 |
| [5] | Ge X H, Han Q L. Distributed fault detection over sensor networks with Markovian switching topologies[J]. International Journal of General Systems , 2014, 43 (3/4) : 305–318. |
| [6] | Wu L G, Shi P, Gao H J. State estimation and sliding-mode control of Markovian Jump singular systems[J]. IEEE Transactions on Automatic Control , 2010, 55 (5) : 1213–1219. DOI:10.1109/TAC.2010.2042234 |
| [7] | Xia J W, Sun C Y, Teng X, et al. Delay-segment-dependent robust stability for uncertain discrete stochastic Markovian jumping systems with interval time delay[J]. International Journal of Systems Science , 2014, 45 (3) : 271–282. DOI:10.1080/00207721.2012.720295 |
| [8] | Zhang L X, Boukas E K. Stability and stabilization of Markovian jump linear systems with partly unknown transition probabilities[J]. Automatica , 2009, 45 (2) : 463–468. DOI:10.1016/j.automatica.2008.08.010 |
| [9] | Hu T, Lin Z, Chen B M. An analysis and design method for linear systems subject to actuator saturation and disturbance[J]. Automatica , 2002, 38 (2) : 351–359. DOI:10.1016/S0005-1098(01)00209-6 |
| [10] | Wang Y J, Zuo Z Q, Cui Y L. Stochastic stabilization of Markovian jump systems with partially unknown transition probabilities and actuator saturation[J]. Circuits, System and Signal Processing , 2012, 31 (1) : 371–383. DOI:10.1007/s00034-011-9297-6 |
| [11] | Liu Y Q, Liu F. Disturbance rejection for Markov jump systems with partly unknown transition probabilities and saturation[J]. Circuits, Systems and Signal Processing , 2013, 32 (6) : 2783–2797. DOI:10.1007/s00034-013-9593-4 |
| [12] | Tian E G, Yue D, Wei G L. Robust control for Markovian jump systems with partially known transition probabilities and nonlinearities[J]. Journal of the Franklin Institute , 2013, 350 (8) : 2069–2083. DOI:10.1016/j.jfranklin.2013.05.011 |
| [13] | Zhao J J, Wang J, Shen H. Dynamic anti-windup control design for Markovian jump delayed systems with input saturation[J]. Circuits, Systems, and Signal Processing , 2013, 32 (5) : 2213–2229. DOI:10.1007/s00034-013-9560-0 |
| [14] | Zhu Q X. Stabilization of stochastically singular nonlinear jump systems with unknown parameters and continuously distributed delays[J]. International Journal of Control, Automation and Systems , 2013, 11 (4) : 683–691. DOI:10.1007/s12555-012-9114-4 |
| [15] | Dong J W, Kim W J. Markov-chain-based output feedback control for stabilization of networked control systems with random time delays and packet losses[J]. International Journal of Control, Automation and Systems , 2012, 10 (5) : 1013–1022. DOI:10.1007/s12555-012-0519-x |
| [16] | Li H P, Shi Y. Robust H∞ filtering for nonlinear stochastic systems with uncertainties and Markov delays[J]. Automatica , 2012, 48 (1) : 159–166. DOI:10.1016/j.automatica.2011.09.045 |
| [17] | Zhang Y Q, Shi P. Observer-based finite-time fuzzy H∞ control for discrete-time systems with stochastic jumps and time-delays[J]. Signal Processing , 2014, 97 (1) : 252–261. |
| [18] | 杨东. 转移概率部分未知的Markovian跳跃系统的H∞控制设计[D]. 曲阜: 曲阜师范大学, 2013. Yang D. Research on H∞ control for Markovian jump system with partially known transition probabilities[D]. Qufu: Qufu Normal University, 2013. |
| [19] | 盛立, 高明. 转移概率部分未知的随机Markov跳跃系统的镇定控制[J]. 控制与决策 , 2011, 26 (11) : 1716–1720. Sheng L, Gao M. Stabilization control of stochastic Markov jump systems with partly unknown transition probabilities[J]. Control and Decision , 2011, 26 (11) : 1716–1720. |
| [20] | Zong G D, Yang D, Hou L L. Robust finite-time H∞ control for Markovian jump systems with partially known transition probabilities[J]. Journal of the Franklin Institute , 2013, 350 (6) : 1562–1578. DOI:10.1016/j.jfranklin.2013.04.003 |
| [21] | Ai Z D, Zong G D. Finite-time stochastic input-to-state stability of impulsive switched stochastic nonlinear systems[J]. Applied Mathematics and Computation , 2014, 245 (10) : 462–473. |
| [22] | Shen M Q, Ye D. Improved fuzzy control design for nonlinear Markovian-jump systems with incomplete transition descriptions[J]. Fuzzy Sets and Systems , 2013, 217 (4) : 80–95. |
| [23] | Wu Z G, Shi P, Su H Y, et al. Stochastic synchronization of Markovian jump neural networks with time-varying delay using sampled-data[J]. IEEE Transactions on Cybernetics , 2013, 43 (6) : 1796–1806. DOI:10.1109/TSMCB.2012.2230441 |



