1 引言
泛化性好且精度高的数学模型,在各行各业中应用广泛.在众多的建模方法中,神经网络是非常重要的一种传统的神经网络,如BP (back propagation) 网络[1-3]、径向基网络[4-6](RBF) 等,所建模型泛化性不是太好,妨碍了其应用.并且,其学习迭代大多基于梯度下降算法,要耗费较长时间.
神经网络的输入信号一般使用的是一个原频谱的信号,若对其进行频率分解,就能突出各子频带的信息,提高信息的致密性.涵盖原始信号频谱的全部子频带也保证了信息的遍历性.较高的致密性和遍历性就能提高神经网络的精度和泛化性[7].文[7]中的频率分解没有自动完成,有必要自动地经过不断地学习进行频率分解.
频率分解需迭代优化,神经网络一般也需迭代学习,两个步骤都存在迭代,就要耗费大量时间.若两个迭代取消一个就节省时间.基于极速学习机的神经网络[8-12]一次计算就完成了学习,避免了该步骤的迭代.针对本文数据集,极速学习机学习约需5 s,40个隐节点的RBF网络学习约需10 min,即同样的数据集下,极速学习机学习速度大大加快.
粒子群优化算法[13-17]对线性和非线性参数优化都有效.粒子群优化算法是模拟群体智能的算法,如蜂群、鸟群和蚁群等.本文采用蚁群的盲动特性对粒子群基本算法进行修缮以自动进行频率分解(以下简称频分),得到优化分布的各子频带.
由此本文提出了一种基于盲动粒子群进行频分的ELM神经网络,用以离线建模.
2 盲动粒子群频分的ELM神经网络 2.1 频分的理论基础设时域信号f(t) 满足绝对可积,则存在傅里叶变换对:
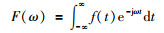
|
(1) |
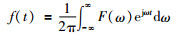
|
(2) |
由式(1) 知,F(ω)=F(-ω).式(2) 变为
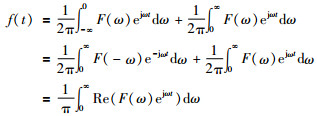
|
设对象的传递函数为G(s),则输出的频率特性与输入的频率特性满足Y(ω)=G(ω)U(ω).有:
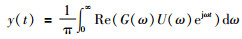
|
令0 < ω1 < ω2 < … < ωn-1 < ωn < ∞,则有:
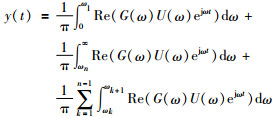
|
(3) |
若将式(3) 中右侧第1个积分里的G(ω) 用通频带为[0,ω1]的理想低通滤波器G0(ω) 代替且在该频带上满足G(ω)=G0(ω),第2个积分里的G(ω) 用通频带为[ωn,∞]的理想高通滤波器Gn(ω) 代替且在该频带上满足G(ω)=Gn(ω),第3个积分里的G(ω) 用通频带为[ωk,ωk+1]的理想带通滤波器Gk(ω) 代替且在该频带上满足G(ω)=Gk(ω),则式(3) 变为
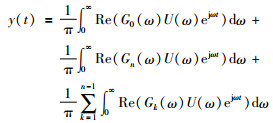
|
(4) |
若G(ω) 事先不知,可用函数逼近算法逼近.式(4) 中各个积分是有界区间,在此进行有界区间内逼近即可.有理函数逼近精度高,本文采用有理函数型Gk(ω) 逼近G(ω).
定义 少量描述曲线或曲面上几何形状的数据点叫型值点.
由文[18]知,若型值点满足一定的条件,有理插值就存在.
定义(m+n+1)×(m+n) 阶矩阵:
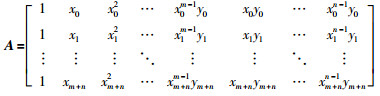
|
令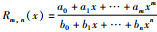
定理1[18] 设型值点(xi,yi)(i=0,1,…,m+n) 中xi互异,有理插值Rm,n(xi)=yi有解的充要条件是各个矩阵Ai(i=0,1,2,…,m+n) 非奇异.其中,Ai是矩阵A去掉第i行后余下的元素按原来的结构次序构成的矩阵,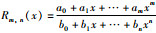
定理2 有理插值函数R0,1(x) 存在的充要条件是任一型值点都不在x轴上.
证明 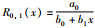
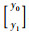
根据定理1,定理2得证,也即任一型值点都不在x轴上.证毕.
定理3 有理插值函数R1,1(x) 存在的充要条件是任两型值点连线都不与x轴平行.
证明 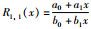
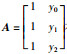
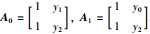
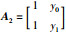
根据定理1,定理3得证.也即任两型值点连线都不与x轴平行.证毕.
定理4 有理插值函数R0,2(x) 存在的充要条件是任一型值点都不在x轴上.
证明 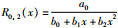
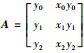
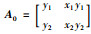
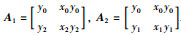
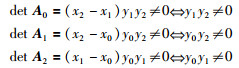
|
根据定理1,定理4得证.也即任一型值点都不在x轴上.证毕.
定理5[19] 有理插值函数R1,2(x) 存在的充要条件是任3点都不在形如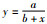
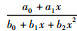
若G(ω) 在有界区间严格单调且不为0,就满足定理2~定理4,一般情况下定理5也能满足.本文采用R0,1(x)、R1,1(x)、R0,2(x) 和R1,2(x) 作为Gk(ω) 进行有界区间逼近.根据连续函数的性质,只要区间较小,逼近精度就较高.
R0,1(x)、R1,1(x)、R0,2(x) 和R1,2(x) 可看作滤波器,采用1阶Butterworth数字滤波器的设计方法就可求得各有理函数[20].
Butterworth滤波器原型的幅频特性是:
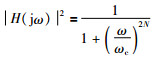
|
其中,N是滤波器阶数,ωc是通带截止频率.
2.2 盲动粒子群算法粒子群智能优化算法是模拟蚁群觅食的仿生算法,其基本思想源于群体中个体之间信息的社会共享和协同进化.用以下数学过程表示PSO算法为:
种群X=[x1,x2,…,xn]T中有n个个体(粒子),种群X的全局极值为G=[g1,g2,…,gn]T.其中,第i个粒子的速度和位置分别是vi=[vi1,vi2,…,vin]T,xi=[xi1,xi2,…,xin]T.个体极值Pi=[pi1,pi2,…,pin]T.在确定全局极值和个体极值后,传统的种群算法用下两式更新第i个粒子的速度和位置:
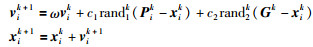
|
(5) |
仔细观察蚂蚁个体的活动,除受群体信息和本体信息的影响外,也存在一定的盲目随机运动,在此对位置式(5) 进行改良,增加一个盲动项:
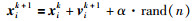
|
(6) |
其中,α是盲动概率,其值选取0.05左右,标示着盲动不是总发生的.
目标函数是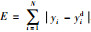
本文中每个粒子的长度代表滤波器个数,即Xi=[ωic1,ωic2,…,ωicm]T标示着有m个截止频率为ωicx的滤波器.种群数是40,即i=1,2,…,40.利用本算法对每个ωicx寻优,使目标函数最小化.解算步骤与基本粒子群算法类似[13-17].
经数值计算仿真,其寻优效果更好.本文采用盲动粒子群算法对滤波器参数寻优.
盲动粒子群算法以3.1节的仿真来佐证.
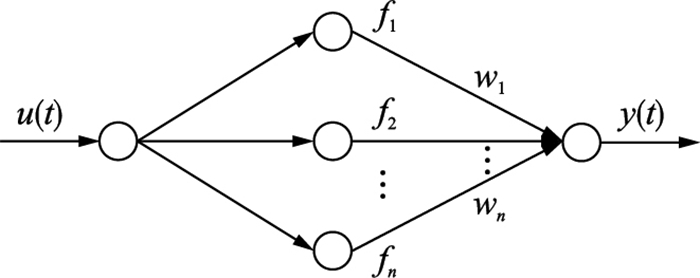
2.3 频分ELM神经网络结构图单输入单输出的ELM神经网络结构如图 1所示. 图 1中每个隐节点即是一个滤波器.低通滤波器对应R0,1(x) 和R0,2(x);带通滤波器对应R1,2(x);全通滤波器对应R1,1(x).
|
| 图 1 极速神经网络结构 Figure 1 The architecture of ELM neural network |
当设计Butterworth滤波器时,此处的低通和带通滤波器通过选择滤波器的阶数和类型来确定.
隐含节点数的个数由采样频率fs来确定,根据Shannon采样定理,一般采样频率越高表明信号的频带越宽,理应划分越多的子频带.经多次仿真测试,频带个数为n=2×round (2fs0.2).
与传统的神经网络比较,图 1也是3层结构,隐节点f1,f2,…,fn是Butterworth滤波器.隐含层到输出层的权值w1,w2,…,wn由极速学习机来确定.
2.4 极速学习机和网络学习极速学习机用来确定w1,w2,…,wn,令隐含层第i个节点的输出为fi(i=1,2,…,n),网络第k次采样输出如式(7) 所示:
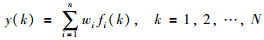
|
(7) |
也可用向量表示为
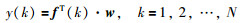
|
其中,N是采样点的个数,w=[w1,w2,…,wn]T,f(k)=[f1(k),f2(k),…,fn(k)]T全部采样值合在一起,可得矩阵方程(8):
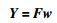
|
(8) |
此处,
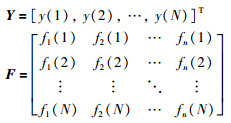
|
由式(8) 得
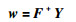
|
(9) |
此处F+是广义逆--Moore-Penrose逆.式(9) 即是极速学习机的原理.
用盲动粒子群算法不断地更新滤波器fi(i=1,2,…,n) 的参数,用式(9) 确定权向量w,使网络逼近精度越来越高,最终完成网络学习.
本网络的泛化性和精度由3.2节的仿真佐证.
3 频分极速神经网络仿真分析 3.1 盲动粒子群算法精度分析选取3个对象:
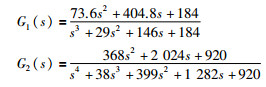
|
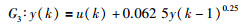
|
式(4) 中的n=7有8个频段,即隐含层有8个节点.种群数是40个粒子,迭代150次.逼近误差如表 1所示.
| 误差 | G1(s) | G2(s) | G3 |
| 盲动 | 0.000 217 7 | 0.003 704 0 | 0.000 941 9 |
| 无盲动 | 0.005 403 7 | 0.004 388 7 | 0.000 942 8 |
从表 1的数据知,同样的条件下盲动粒子群算法的逼近精度高于无盲动的.对线性系统,精度提高较多.对非线性系统,精度提高较少.
最大相对误差是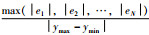
同样用以上的3个对象,用本文模型与常规RBF模型对比.
建模学习信号为
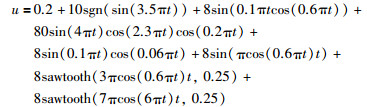
|
其中sawtooth为锯齿波函数.建模信号复杂,是为了有较高的遍历性.随意选取3个测试泛化性能的信号是:
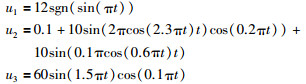
|
测试时,神经网络的隐节点都取8个,学习150次.记录最大相对误差.
本文模型中网络输出值的数据如表 2所示.
| 信号 | G1(s) | G2(s) | G3 |
| u(t) | 0.000 219 5 | 0.000 518 2 | 0.000 942 4 |
| u1(t) | 0.008 849 3 | 0.004 077 2 | 0.003 978 9 |
| u2(t) | 0.000 741 0 | 0.000 779 5 | 0.002 489 0 |
| u3(t) | 0.000 050 7 | 0.000 659 8 | 0.001 029 0 |
从表 2所得,学习时最大相对误差较小.用其它3个信号测试泛化性,最大相对误差稍大,在千分之几,精度有所下降,但千分之几的误差,是能满足一般工程需求的.比如就可用于一般工业自动控制领域的PID参数离线整定.
RBF模型中网络输出值的数据如表 3所示.
| 信号 | G1(s) | G2(s) | G3 |
| u(t) | 0.000 000 0 | 0.000 000 0 | 0.000 000 0 |
| u1(t) | 3.301 710 9 | 2.333 406 6 | 5.165 852 8 |
| u2(t) | 3.243 650 7 | 2.271 811 4 | 3.537 169 3 |
| u3(t) | 1.231 739 6 | 0.917 577 4 | 1.363 363 9 |
从表 3所得,学习时最大相对误差为0.用其它3个信号测试泛化性,最大相对误差非常大,泛化性很差,不能满足一般工程需求的.
比较表 2和表 3知,本文模型的泛化性大大好于常规RBF的泛化性.千分之几的最大相对误差对应控制仪表的0.2~1.0精度等级,可用于工程中.
4 结论用盲动粒子群频分ELM神经网络,对3个对象离线建模,泛化性达到千分之几的精度,可以应用于一般工程当中.仿真结果表明,本算法是有效的.如何进一步提高泛化精度,使最大相对误差达到万分之几的精度;如何进行在线建模是后续研究的方向.
| [1] | Yu F, Xu X Z. A short-term load forecasting model of natural gas based on optimized genetic algorithm and improved BP neural network[J]. Applied Energy, 2014, 134 (12): 102–113. |
| [2] | Xu Y J, You T, Du C L. An integrated micromechanical model and BP neural network for predicting elastic modulus of 3-D multi-phase and multi-layer braided composite[J]. Composite Structures, 2015, 122 (4): 308–315. |
| [3] | Cheng C, Cheng X S, Dai N. Prediction of facial deformation after complete denture prosthesis using BP neural network[J]. Computers in Biology and Medicine, 2015, 66 (11): 103–112. |
| [4] | Zhou F, Peng H, Qin Y, et al. RBF-ARX model-based MPC strategies with application to a water tank system[J]. Journal of Process Control, 2015, 34 : 97–116. DOI:10.1016/j.jprocont.2015.07.010 |
| [5] | Qin Y, Peng H, Zhou F, et al. Nonlinear modeling and control approach to magnetic levitation ball system using functional weight RBF network-based state-dependent ARX model[J]. Journal of the Franklin Institute, 2015, 352 (10): 4309–4338. DOI:10.1016/j.jfranklin.2015.06.014 |
| [6] | Herrera L J, Pomares H, Rojas I, et al. Global and local modelling in RBF networks[J]. Neurocomputing, 2011, 74 (16): 2594–2602. DOI:10.1016/j.neucom.2011.03.027 |
| [7] | 刘加存, 梅其祥, 李春辉. 基于频分神经网络和预测控制的PID参数整定研究[J]. 系统仿真学报, 2014, 26 (5): 1176–1179. Liu J C, Mei Q X, Li C H. The research of PID tuning based on frequency divide neural network and model predictive control[J]. Journal of System Simulation, 2014, 26 (5): 1176–1179. |
| [8] | Liu X, Wan A H. Universal consistency of extreme learning machine for RBFNs case[J]. Neurocomputing, 2015, 168 (11): 1132–1137. |
| [9] | Li J, Hua C, Tang Y, et al. A fast training algorithm for extreme learning machine based on matrix decomposition[J]. Neurocomputing, 2016, 173 (1): 1951–1958. |
| [10] | Shao Z F, Meng J E. An online sequential learning algorithm for regularized extreme learning machine[J]. Neurocomputing, 2016, 173 (1): 778–788. |
| [11] | 刘菲菲, 彭荻, 贺彦林, 等.基于极限学习的过程神经网络研究及化工应用[J].上海交通大学学报, 2014, 48(7):977-981. Liu F F, Peng D, He Y L, Zhu Q X. Research and chemical application of extreme learning based process neural network[J]. Journal of Shanghai Jiao Tong University, 2014, 48(7):977-981. http://xuebao.sjtu.edu.cn/CN/Y2014/V48/I07/977 |
| [12] | 石红伟, 杨明红. 基于ELM的跨越前馈神经网络及其应用研究[J]. 现代电子技术, 2013, 36 (15): 108–111. Shi H W, Yang M H. Span feedforward neural network based on ELM and its application[J]. Modern Electronics Technique, 2013, 36 (15): 108–111. |
| [13] | Marinakis Y. An improved particle swarm optimization algorithm for the capacitated location routing problem and for the location routing problem with stochastic demands[J]. Applied Soft Computing, 2015, 37 (12): 680–701. |
| [14] | Jia Y F, Chi S C. Back-analysis of soil parameters of the Malutang Ⅱ concrete face rockfill dam using parallel mutation particle swarm optimization[J]. Computers and Geotechnics, 2015, 65 (4): 87–96. |
| [15] | Farahmand H, Rashidinejad M, Mousavi A. Hybrid mutation particle swarm optimisation method for available transfer capability enhancement[J]. Electrical Power and Energy Systems, 2012, 42 (11): 240–249. |
| [16] | 余玉丰, 李国, 徐晨. 基于分组的PSO与DE的混合算法[J]. 计算机应用研究, 2014, 31 (8): 2294–2298. Yu Y F, Li G, Xu C. Hybrid algorithm based on grouped PSO and DE[J]. Application Research of Computers, 2014, 31 (8): 2294–2298. |
| [17] | Zhou X J, Yang C H, Gui W H, et al. A particle swarm optimization algorithm with variable random functions and mutation[J]. Acta Automatica Sinica, 2014, 40 (7): 1339–1347. DOI:10.1016/S1874-1029(14)60015-X |
| [18] | Macon N, Dupree D E. Existence and uniqueness of interpolating rational function[J]. American Mathematical monthly, 1962, 69 (8): 751–759. DOI:10.2307/2310771 |
| [19] | 唐杨新.有理函数逼近若干问题研究[D].合肥:合肥工业大学, 2009. Tang Y X, Some problem research on rational function approximants[D]. Hefei:Hefei University of Technology, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10359-2009155885.htm |
| [20] | 王大伟, 贾荣丛, 王划一. 基于Matlab的巴特沃斯滤波器设计[J]. 现代电子技术, 2012, 35 (21): 71–72. Wang D W, Jia R C, Wang H Y. Design of butterworth analog filter based on Matlab[J]. Modern Electronics Technique, 2012, 35 (21): 71–72. |



