2. 浙江三门县人民医院, 浙江 台州 317100
2. Sanmen County People's Hospital, Taizhou 317100, China
1 引言
聚类分析[1-2]是数据挖掘[3-4]的重要组成部分,作为数据分析的工具,聚类在各个领域得到了广泛的应用[5].所谓聚类(clustering)是将数据对象分成若干个类,在同一个类中的对象具有较高的相似度,而不同类中的对象差别较大.作为无监督[6]的学习方法之一,聚类[7]越来越引起人们的关注.
聚类算法[7]大体分为以下几类:(1) 基于划分[8]的方法,如K-means算法[9]、K-medoids算法等;(2) 基于层次的方法,如BIRCH(balanced iterative reducing and clustering using hierarchies)算法、CURE(clustering using representatives)[10]算法;(3) 基于密度的方法,如DBSCAN (density-based spatial clustering of application with noise)[1, 11]算法、DENCLUE(DENsity based CLUstEring)等算法;(4) 基于网格的方法;(5) 神经网络等其它各种聚类方法[10-13].其中,K-means算法是最经典的聚类算法之一.作为目前应用最广的基于划分的聚类算法,K-means算法实现起来比较简单,但是仍有以下3个缺点:(1) 用户必须事先指定聚类个数;(2) K-means算法不适合发现非凸状的聚类;(3) K-means算法对噪声和异常数据非常敏感.而DBSCAN通过检查一个对象ε邻域的密度是否足够高,即一定距离ε内数据点个数是否超过设定阈值来确定是否建立一个以该对象为核心对象的新簇,再合并密度可达簇的方法来实现可以在带有“噪声”的空间数据库中发现任意形状的簇类,但是DBSCAN算法却对ε和设定阈值这两个难以确定的参数敏感[1].另外,在计算复杂度上,DBSCAN相对较高.
针对以上分析的K-means算法及DBSCAN算法的缺点,本文提出一种新的基于竞争思想的分级聚类(hierarchical clustering)算法,将竞争思想引入聚类过程,用多级快速凸聚类,解决非凸聚类问题,采用权重判据以及权重增加的方式计算联系性权重,实现后级小簇快速合并算法.实验结果表明,本文算法聚类时间短、速度快准确率高,不仅能发现任意形状的簇类,而且计算复杂度及参数敏感性低于DBSCAN算法.
2 相关定义及算法描述本文采用分级聚类的思想,将聚类过程分为2级聚类.第1级聚类基于距离,将对象划分为一定数目的小类;第2级聚类基于竞争思想[14-16],计算第1级聚类簇心之间的权重,采取适当的规则进行簇的合并,实现聚类.算法的基本思想为:
设数据集X={X1,X2,…,Xi,…,XN}(i=1,2,…,N),其中,N是数据集中的元素总数,X中的第i个数据对象Xi是一个P维矢量,Xi=[xi1,xi2,…,xii,…,xip]T. X中对象间的距离的计算方法为
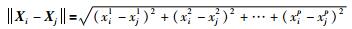
|
(1) |
其中,Xi=[xi1,xi2,…,xip],Xj=[xj1,xj2,…,xjp]是X的两个P维数据对象.
2.1 第1级聚类第1级聚类是在给定的ε邻域值基础上进行一次次遍历,形成第1级聚类的小簇.在遍历的过程中取所要遍历数据集中的第1个数据作为第1个小簇的簇心,依次遍历数据集中的下一个数据,按照式(1) 计算数据点到所有簇心的距离,在簇心的ε邻域时将该点放入簇心所在的簇中,不在簇心的ε邻域时,该点作为一个新的簇的簇心计入下一次点到所有簇心的计算过程中.直到对所有数据进行一次遍历.最后将所形成小簇的中心更新为该簇的实际簇心.
第1级聚类算法描述如下:
对于数据集X={X1,X2,…,Xi,…,XN},设定距离半径ε及权重阈值L;假设最终形成的簇为H={H11,H21,…,Hj1,…,HM1},每一个簇所对应的簇心为C={C11,C21,…,Cj1,…,CM1},Cj1和Hj1中的上标1是代表第1级的聚类,下标j代表第j个簇.
第1步 初始化i=1,j=1,C11=X1.
第2步 i=i+1.
第3步 从第1个簇心C11开始一直到第j个簇心依次作如下处理:
如果存在一个j使得||Xi-Cj1|| < ε,那么Hj1={Hj1,Xi}并且判断i取值.当i < N时,返回第2步;否则,执行第4步.
如果找不到一个j满足||Xi-Cj1|| < ε,那么j=j+1,同时将Xi放入新的簇Hj1中,Hj1={Xi}并且判断i取值.当i < N时,返回第2步;否则,执行第4步.
第4步 对形成的小簇H={H11,H21,…,Hj1,…,HM1}进行簇心的更新,将簇的实际中心作为更新后的簇心C={C11,C21,…,Cj1,…,CM1}.
2.2 第2级聚类由于第1级聚类形成的是一些基于欧氏距离数据空间中的凸状的、分布相对密集的小类,所以需要进行凸状小簇的合并(第2级聚类)来解决非凸状等复杂聚类问题.为了对小簇进行合理合并,引入簇间联系权重的计算.
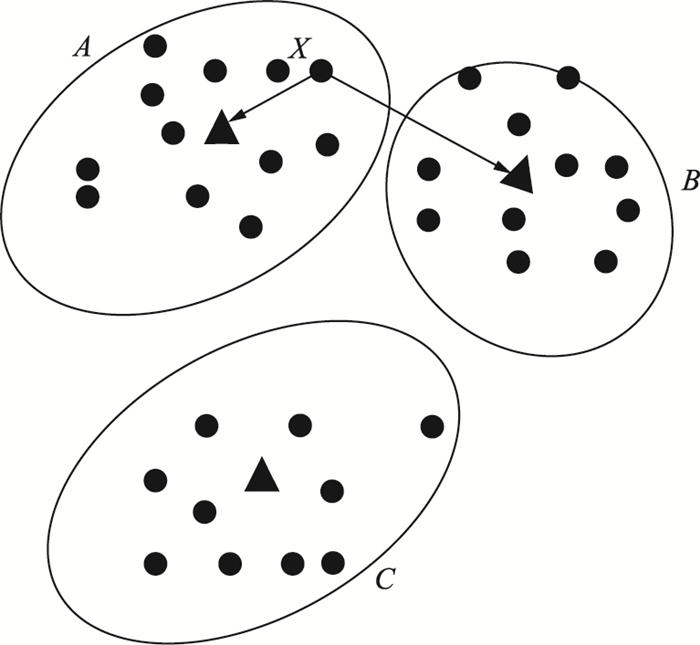
如图 1所示,图中3个椭圆分别代表3个小簇,实心点为簇心元素,空心三角形代表该簇的簇心,簇心记为A、B、C.为方便表述,分别称3个小簇为簇A、簇B、簇C.对簇A中的数据Xi,距离Xi最近簇心默认为Xi所在的簇A的簇心,如果除去Xi本身所在的簇心外,距离Xi次近的簇为小簇B,此时,称簇A和簇B之间对于数据Xi存在联系权重.
|
| 图 1 簇之间的联系 Figure 1 The links among the clusters |
所有簇心对于簇中数据存在竞争关系,本文在竞争中采用“赢者通吃”的思想,取竞争过程中该元素自身所在簇的簇心和除去自身簇心之外的距离该元素最近的簇心作为竞争中的胜利者,进行联系权重计算.如图 1中簇C对簇A、B间关于当前元素Xi的联系权重没有影响.
从簇间联系权重的概念可以看出,2个小簇之间的联系权重实际上取决于小簇之间数据点的密度.由此,可以制定基于联系权重计算的小簇之间合并准则.
联系权重的考虑分为2个层次:第1层次是簇间联系权重的存在判据;第2层次是对已存在权重的加权计算.联系权重存在判据:对数据集X={X1,X2,…,Xi,…,XN},在进行第1级聚类之后,若所有簇心对数据Xi的竞争过程中,胜利者分别为簇心Cx1和Cy1,取d=max(||Xi-Cx1||,||Xi-Cy1||).当d的取值在某一范围时,则认为簇Cx1和簇Cy1存在联系性权重.实验结果表明,当d≤2.5时,算法具有较好的聚类质量.本文取d≤2.5进行联系权重的存在判据.联系性权重的增加准则:用Lxy表示两个小簇之间的联系权重,计算方法为
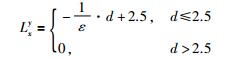
|
(2) |
其中,d=max(||Xi-Cx1||,||Xi-Cy1||),Lxy中x=min(x,y),y=max(x,y),ε为第1级聚类的聚类半径.
基于上述联系权重的存在判据和增加准则,在第1级聚类的基础上计算小簇之间的联系权重:
首先对数据集X={X1,X2,…,Xi,…,XN}从第1个数据X1开始依次进行遍历,对每一个具体的数据,所有簇心C={C11,C21,…,Cj1,…,CM1}对该数据存在竞争关系,按照“赢者通吃”的思想找出所有簇心在对数据竞争关系过程中的2个胜利者Cx1和Cy1,然后按照上面所说联系性权重存在准则判断2个胜利者所对应的簇Hx1和Hy1之间是否存在联系权重.如果存在权重,则对存在权重的簇按照式(2) 进行联系权重的增加,然后遍历下一个数据;如果不存在联系权重则直接遍历下一个数据.直到所有的数据依次遍历一次.
联系权重计算完成之后,形成的联系权重为Lxy,其中x=1,…,M,y=x,…,M.
根据以上对第1级聚类形成的凸状的、分布相对密集的小簇之间联系性权重的计算,进行小簇合并.给定联系权重阈值L,当联系权重Lxy>L时,簇Hx1和簇Hy1可以合并,第2级聚类算法描述为:
第1步 假设最终形成的簇集合为Qk,其中下标k的每一个取值对应一个独立的簇,对最终形成的簇集合Qk的下标初始化为k=1,Q1={C11},联系权重Lxy下标x初始化为x=1.
第2步 联系权重Lxy的下标x=1,…,M逐一取值,对联系权重Lxy的上标取值依次为y=x,…,M,当Lxy中出现x=y的情况时,令Lxy满足Lxy>L.
当联系权重Lxy不满足Lxy>L条件时,小簇不作任何处理;当联系权重Lxy满足Lxy>L条件时,如果Cx1∈Qk或者Cy1∈Qk,那么Cx1和Cy1同时合并到Qk中,Qk={Qk,Cx1,Cy1};否则k=k+1,同时Cx1和Cy1合并到新的簇Qk中,Qk={Cx1,Cy1}.其中,Qk={Qk,Cx1,Cy1}和Qk={Cx1,Cy1}中存在的相同的元素合并为同一项.
第3步 最终形成的簇为Qk(k=1,2…,K).
第2级聚类结束.
由于第2级聚类对凸状的、分布相对密集的小类采用的合并方式是一种联合覆盖的形式,因此可以很好地解决一些非凸状等复杂聚类问题.
3 实验结果与分析本文实验环境为Intel酷睿i5-3230M CPU @ 2.60 GHz,安装内存4.00 GB,500 GB硬盘,Windows 7操作系统,Matlab R2011b.
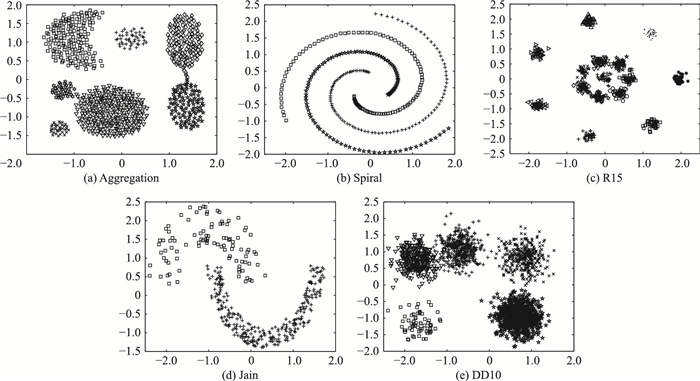
3.1 不加噪声的数据集实验为了测试本文算法,将本文算法与经典的K-means算法和基于密度的DBSCAN算法进行对比,选用图 2所示的聚类算法测试常用数据集进行实验.
|
| 图 2 实验所用测试数据集 Figure 2 Test data set for the experiment |
为了测试本文对非凸集的处理能力,选用了几种咬合形数据及螺旋线数据.同时,为了测试算法对大数据的处理能力,选用的DD10数据集是包含2 000个数据的大数据集.另外,为了测试本文对高维数据的处理能力,选用UCI机器学习数据库中的Iris聚类算法测试数据集.为了更方便清晰地展示本文算法的测试结果,采用表 1中对数据集的描述方式.
| 数据集 | 数据集代码 | 样本数 | 属性数 | 类数 |
| Aggregation | D1 | 788 | 2 | 7 |
| Spiral | D2 | 312 | 2 | 3 |
| R15 | D3 | 600 | 2 | 15 |
| Jain | D4 | 373 | 2 | 2 |
| DD10 | D5 | 2 000 | 2 | 5 |
| Iris | D6 | 150 | 4 | 3 |
衡量聚类有效性[17-18]的指标之一是聚类准确率.聚类准确率γ为正确分类的数据数目占总数据数目的百分比.本文首先采用聚类准确率来测试本文算法的效果.对表 1所列的6种数据集分别在K-means算法、基于密度的DBSCAN算法和本文算法上各自运行20次,统计出20次算法运行的正确率γ,计算出20次结果的平均正确率,结果如表 2所示.
| 数据集 | K-means | DBSCAN | 本文算法 |
| D1 | 0.789 2 | 0.789 3 | 0.956 8 |
| D2 | 0.339 4 | 0.992 0 | 0.999 9 |
| D3 | 0.730 8 | 0.945 0 | 0.971 7 |
| D4 | 0.782 7 | 0.975 0 | 0.994 6 |
| D5 | 0.665 3 | 0.797 0 | 0.826 0 |
| D6 | 0.779 3 | 0.660 0 | 0.800 0 |
根据表 2结果,本文算法在6种数据集上的准确率均高于K-means算法和基于密度的DBSCAN算法.本文算法不仅适用于凸集数据,在非凸集数据集上聚类准确率仍然较好.同时,本文算法对高维数据效果也略好于K-means算法和DBSCAN算法.在数据集D1和数据集D5上,本文算法的准确率均明显高于基于密度的DBSCAN.分析原因,DBSCAN算法会对每一个数据点检查该点的ε邻域及该点直接或间接密度可达的簇,因此容易将具有连接的不同的簇类划分到一个簇中,而本文算法在第2级聚类的类的合并处理上,采用增加权重的处理方式,权重达不到阈值,不进行簇的合并,因此在具有连接的数据集处理上,本文算法效果比DBSCAN要好.
根据表 3,K-means算法的最高准确率和最低准确率变化幅度较大,聚类结果具有一定的随机性,而本文算法和基于密度的DBSCAN算法一样,具有较好的聚类稳定性.
| 数据 | K-means | DBSCAN | 本文算法 | |||
| 最高 | 最低 | 最高 | 最低 | 最高 | 最低 | |
| D1 | 0.819 7 | 0.682 7 | 0.789 3 | 0.789 3 | 0.956 8 | 0.956 8 |
| D2 | 0.333 3 | 0.352 5 | 0.992 0 | 0.992 0 | 0.999 9 | 0.999 9 |
| D3 | 0.799 4 | 0.666 2 | 0.945 0 | 0.945 0 | 0.971 7 | 0.971 7 |
| D4 | 0.782 9 | 0.779 1 | 0.975 0 | 0.975 0 | 0.994 6 | 0.994 6 |
| D5 | 0.897 5 | 0.550 0 | 0.797 0 | 0.797 0 | 0.826 0 | 0.826 0 |
| D6 | 0.826 6 | 0.566 7 | 0.660 0 | 0.660 0 | 0.800 0 | 0.800 0 |
常用的聚类有效性评价方法有外部评价法、内部评价法和相对评价法[19-20].这3类准则中,外部准则最为客观.为了进一步评价本文算法的性能,下面采用最为客观的外部准则中的Rand指数、Jaccard系数和Adjusted Rand index参数对算法的聚类结果进行分析. Rand指数、Jaccard系数和Adjusted Rand index参数的定义如下:设数据集X={X1,X2,…,Xi,…,XN},X本身正确的聚类划分为U,通过某种算法对数据集处理得到的某种聚类划分为V,对X中的一对数据点(Xi,Xj),进行如下项的计算:
φUV——两个数据点(Xi,Xj)属于U且属于V;
φUV′——两个数据点(Xi,Xj)属于U,但不属于V;
φU′V——两个数据点(Xi,Xj)不属于U,但属于V;
φU′V′——两个数据点(Xi,Xj)不属于U,也不属于V.
设a、b、c、d分别表示φUV、φUV′、φU′V、φU′V′的数目,则a+b+c+d=N(N-1)/2,N为数据集X中所含的样本数,即数据集的规模.定义M为数据集X中所有可能的样本对,M=a+b+c+d.
Rand指数:
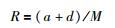
|
Jaccard系数:
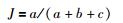
|
Adjusted Rand index参数:
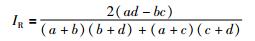
|
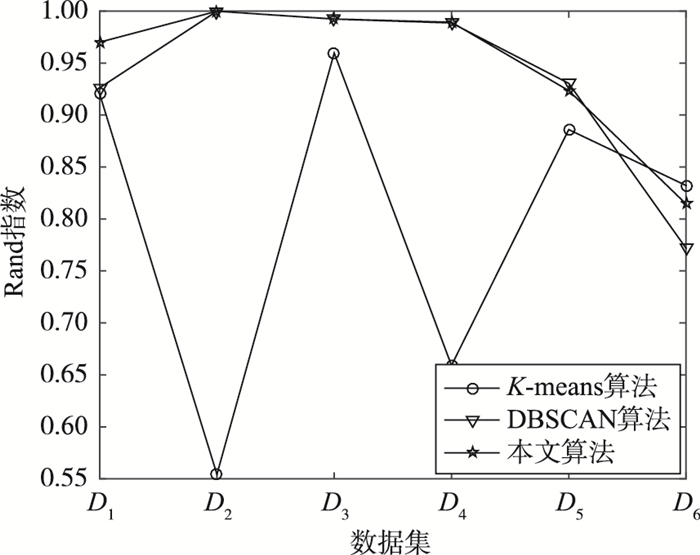
Rand指数和Jaccard系数的取值为[0,1],Rand指数表示聚类结果与原始数据集样本分布的一致性,Jaccard系数表示正确分类的样本对数目占聚类前或聚类后在同一簇的样本对数目的比例. IR取值为[-1,1],IR取值越接近1,则聚类结果与原始样本正确分布的一致性越高. IR值越大表示正确聚类的样本对越多,聚类效果越好.文[21]指出Adjusted Rand index参数是评价聚类有效性的最好准则,本文算法和K-means算法及DBSCAN算法的3个系数比较如图 3~图 5所示.
|
| 图 3 Rand指数比较 Figure 3 The comparison of the Rand index |
|
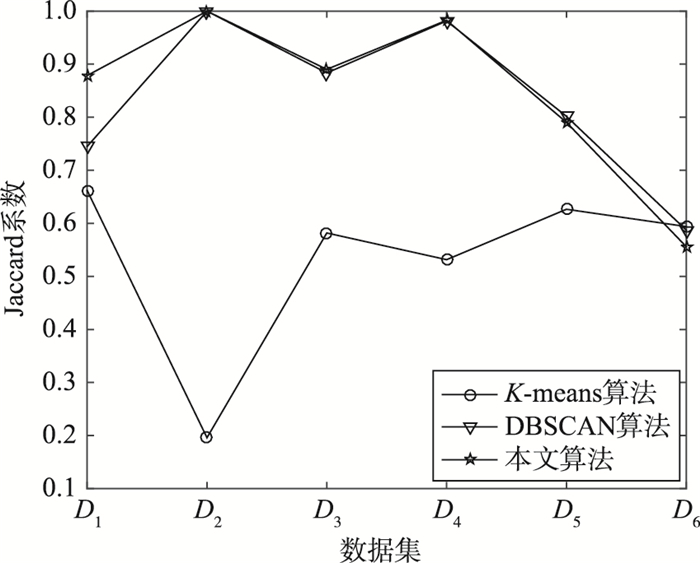
| 图 4 Jaccard参数比较 Figure 4 The comparison of the Jaccard index |

|
| 图 5 Adjuested Rand index参数比较 Figure 5 The comparison of the Adjuested Rand index |
通过图 3~图 5可以看出,在数据集D1~D5中,本文算法的3个参数值均高于K-means算法,而与基于密度的DBSCAN算法基本相当.在数据集D1中,本文算法的测试结果显示,3个参数值本文均高于K-means和DBSCAN.
在算法复杂度上,K-means的复杂度是O(nkt),其中,n是所有对象的数目,k是簇的数目,t是迭代的次数.如果采用空间索引,DBSCAN的计算复杂度是O(nln n),这里n是数据集中对象的数目;否则,计算复杂度是O(n2).对于本文算法,在复杂度上由于本文算法没有对每个数据点计算ε邻域,而是直接遍历2遍数据集完成聚类,因此复杂度低于DBSCAN,而会略高于K-means算法.虽然本文算法计算复杂度略高于K-means算法,但是K-means算法性能有限,不适用于广泛的非凸状聚类. 表 4给出3种算法在6种数据集上的运行时间.从表 4可以看出,本文在运行时间方面与DBSCAN算法相比具有一定的优越性.
| 数据集 | K-means | DBSCAN | 本文算法 |
| D1 | 0.016 0 | 0.058 3 | 0.048 0 |
| D2 | 0.012 4 | 0.025 8 | 0.022 6 |
| D3 | 0.018 8 | 0.060 9 | 0.024 9 |
| D4 | 0.010 0 | 0.059 5 | 0.022 7 |
| D5 | 0.020 0 | 0.224 1 | 0.126 7 |
| D6 | 0.009 6 | 0.073 0 | 0.008 1 |
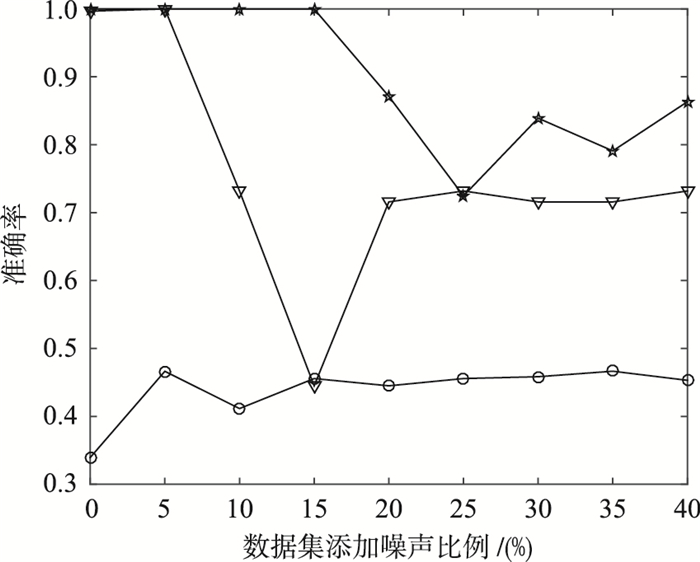
为进一步测试本文算法的抗干扰能力,本文对上面所用的非凸状数据集D4螺旋线数据随机生成了含有5%、10%、15%、20%、25%、30%、35%、40%的随机噪声进行测试.测试结果的聚类准确率如图 6所示.
|
| 图 6 人工添加噪声数据集上聚类准确度比较 Figure 6 The comparison of the clustering accuracy on the artificial additive noise data set |
图 6的比较结果显示,本文算法在含有不同比例的噪声数据集上的聚类准确度明显高于K-means算法,而在含有较高的噪声比例的数据集上略优于DBSCAN算法,在含有较低的噪声比例的数据集上,抗噪声能力与DBSCAN算法相当.
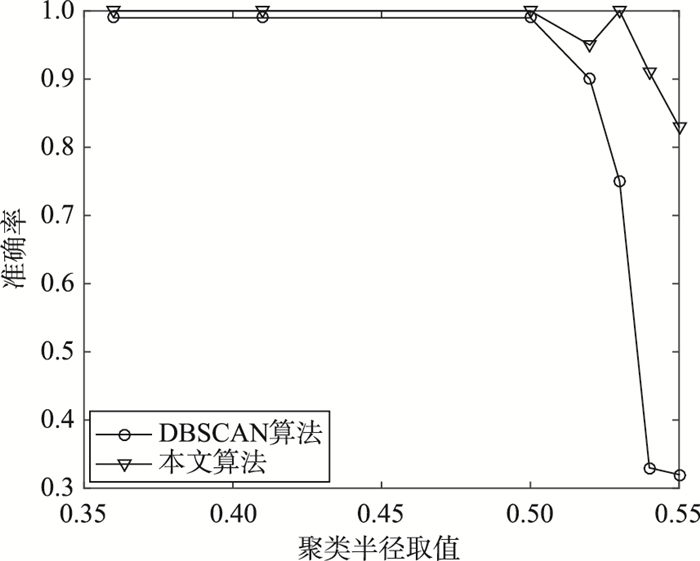
3.3 算法参数敏感性实验本文算法同DBSCAN算法一样,都是在人为给定参数和阈值的基础上进行的,阈值对测试结果无疑有着重要的影响.本文所提算法的2个参数(ε邻域值和联系权重阈值L)的选取分别影响2级聚类的过程.但是ε值的大小只能决定第1级聚类所形成的小簇的数目及小簇中数据的个数,而联系权重阈值L的取值则最终决定小簇是否能够合并.经多次实验后发现,本文ε邻域值选取数据所占用空间的10%左右较为合理,联系权重阈值L的取值取为有联系权重的2个小簇中所有数据数目和的40%到50%左右是一个比较合理的数据,同时对大部分数据具有良好的效果.而文[1]指出,对于最初的DBSCAN算法,设定阈值在4的时候对于大部分2维数据集是一个合理的值.因此,为了比较参数敏感性,本文选取本文算法和DBSCAN算法都能很好处理的数据集D2的Spiral螺旋线数据集进行比较,重点比较DBSCAN中的ε邻域及本文算法第1级聚类中的ε邻域的参数敏感性.对于数据集D2依次取ε值为数据空间的8%、9%、10%、11.5%、11.7%、12%、12.3%,对应的ε取值分别为0.36、0.45、0.495、0.52、0.53、0.54、0.55,实验结果如图 7所示.
|
| 图 7 参数敏感性比较 Figure 7 The comparison of the parameter sensitivity |
图 7的比较结果显示,本文算法和DBSCAN算法当ε邻域半径取值为数据空间的8%、9%、10%、11.5%时都具有良好的聚类效果,说明该取值是比较合理的.但是,当取值进行0.03%小范围变动时,DBSCAN算法的聚类准确度急剧下降,而本文算法依然可以保持在0.8以上的聚类准确度,这说明本文算法参数敏感性低于BSCAN算法.
4 结语本文分析了K-means算法及DBSCAN算法的不足,在此基础上提出了针对非凸状等复杂聚类的一种新的基于竞争思想的分级聚类算法,采用多级快速凸聚类,解决非凸聚类问题,克服了K-means算法不能解决的非凸状聚类问题的缺点.算法聚类时间短、准确率高.另外采用增加小簇之间联系性权重的方式进行小簇的合理合并,避免了小簇之间联系性权重的全连接,只对存在联系性的小簇之间建立联系性权重,减少了权重的计算,缩小了程序存储空间.算法在计算复杂度和参数敏感性方面优于DBSCAN算法.实验结果表明了本文算法的准确性、快速性及良好的抗噪性.鉴于本算法高效快速的特点,下一步将研究其在高维数据领域的应用.
| [1] |
范明, 范宏建.
数据挖掘导论[M]. 北京: 人民邮电出版社, 2011: 305-400.
Fan M, Fan H J. Introduction to data mining[M]. Beijing: Posts & Telecom Press, 2011: 305-400. |
| [2] |
王骏, 王士同, 邓赵红.
聚类分析研究中的若干问题[J]. 控制与决策, 2012, 27(3): 321–328.
Wang J, Wang S T, Deng Z H. Survey on challenges in clustering analysis research[J]. Control and Decision, 2012, 27(3): 321–328. |
| [3] |
杨黎刚, 苏宏业, 张英, 等.
基于SOM聚类的数据挖掘方法及其应用研究[J]. 计算机工程与科学, 2007, 29(8): 133–136.
Yang L G, Su H Y, Zhang Y, et al. A method of data mining based on SOM clustering and its application[J]. Computer Engineering & Science, 2007, 29(8): 133–136. |
| [4] | Celebi M E, Kingravi H A, Vela P A. A comparative study of efficient initialization methods for the K-means clustering algorithm[J]. Expert Systems with Applications, 2013, 40(1): 200–210. DOI:10.1016/j.eswa.2012.07.021 |
| [5] |
李大字, 钱丽, 靳其兵, 等.
改进的全局K'-means算法及其在数据分类中的应用[J]. 信息与控制, 2011, 40(1): 100–104.
Li D Z, Qian L, Jin Q B, et al. modified global K'-means algorithm and its application to data clustering[J]. Information and Control, 2011, 40(1): 100–104. |
| [6] | Bohte S M, La Poutré H, Kok J N. Unsupervised clustering with spiking neurons by sparse temporal coding and multilayer RBF networks[J]. IEEE Transactions on Neural Networks, 2002, 13(2): 426–435. DOI:10.1109/72.991428 |
| [7] |
苏卫星, 朱云龙, 刘芳, 等.
基于改进模糊聚类的同构多传感器在线数据融合方法[J]. 信息与控制, 2015, 44(5): 557–563.
Su W X, Zhu Y L, Liu F, et al. online data fusion method for homogeneous multi-sensors based on advanced fuzzy clustering[J]. Information and Control, 2015, 44(5): 557–563. |
| [8] |
王赛芳, 戴芳, 梁波, 等.
一种基于路径的划分聚类算法[J]. 信息与控制, 2011, 40(1): 141–144.
Wang S F, Dai F, Liang B, et al. a path-based clustering algorithm of partition[J]. Information and Control, 2011, 40(1): 141–144. |
| [9] | Na S, Xumin L, Yong G. Research on K-means clustering algorithm:An improved K-means clustering algorithm[C]//2010 Third International Symposium on Intelligent Information Technology and Security Informatics (ⅡTSI). Piscataway, NJ, USA:IEEE, 2010:63-67. |
| [10] |
李军, 黄杰.
基于自组织映射神经网络的局部自回归方法在网络流量预测中的应用[J]. 信息与控制, 2016, 45(1): 120–128.
Li J, Huang J. Prediction of network traffic using local auto-regressive methods based on self-organizing map neural network[J]. Information and Control, 2016, 45(1): 120–128. |
| [11] | Zhou S, Zhou A, Jin W, et al. FDBSCAN:A fast DBSCAN algorithm[J]. Journal of Software, 2000, 11(6): 735–744. |
| [12] | Rodriguez A, Laio A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492–1496. DOI:10.1126/science.1242072 |
| [13] | Ding L, Gonzalez-Longatt F M, Wall P, et al. Two-step spectral clustering controlled islanding algorithm[J]. IEEE Transactions on Power Systems, 2013, 28(1): 75–84. DOI:10.1109/TPWRS.2012.2197640 |
| [14] | Celebi M E, Kingravi H A, Vela P A. A comparative study of efficient initialization methods for the K-means clustering algorithm[J]. Expert Systems with Applications, 2013, 40(1): 200–210. DOI:10.1016/j.eswa.2012.07.021 |
| [15] |
段敏, 张锡恩.
基于合并思想和竞争学习思想的聚类新算法[J]. 计算机工程与设计, 2006, 27(9): 1656–1659.
Duan M, Zhang X E. Novel clustering algorithm based on combination ideal and competitive learning idea[J]. Computer of Engineering and Design, 2006, 27(9): 1656–1659. |
| [16] | ZhiMao L U, Qi Z. Clustering by data competition[J]. Science China:Information Sciences, 2013, 56(1): 12105–012105. |
| [17] |
周开乐, 杨善林, 丁帅, 等.
聚类有效性研究综述[J]. 系统工程理论与实践, 2014, 34(9): 2417–2431.
Zhou K L, Yang S L, Ding S, et al. On cluster validation[J]. Systems Engineering -Theory & Practice, 2014, 34(9): 2417–2431. DOI:10.12011/1000-6788(2014)9-2417 |
| [18] | Arbelaitz O, Gurrutxaga I, Muguerza J, et al. An extensive comparative study of cluster validity indices[J]. Pattern Recognition, 2013, 46(1): 243–256. DOI:10.1016/j.patcog.2012.07.021 |
| [19] |
张惟皎, 刘春煌, 李芳玉.
聚类质量的评价方法[J]. 计算机工程, 2005, 31(20): 10–12.
Zhang W J, Liu C H, Li F Y. Method of quality evaluation for clustering[J]. Computer Engineering, 2005, 31(20): 10–12. DOI:10.3321/j.issn:1002-8331.2005.20.003 |
| [20] |
金建国.
聚类方法综述[J]. 计算机科学, 2014, 41(B11): 288–293.
Jin J G. Review of clustering method[J]. Computer Science, 2014, 41(B11): 288–293. |
| [21] | Vinh N X, Epps J, Bailey J. Information theoretic measures for clusterings comparison:is a correction for chance necessary?[C]//Proceedings of the 26th Annual International Conference on Machine Learning. New York, NJ, USA:ACM, 2009:1073-1080. |



