2. 福建工程学院控制与信息技术研究所, 福建 福州 350108;
3. 建国科技大学自动化工程系, 台湾 彰化 50094
2. Institute of Control and Information Technology, Fujian University of Technology, Fuzhou 350108, China;
3. Department of Automation Engineering, Chienkuo Technology University, Changhua 50094, China
1 引言
得益于微电子和微加工技术,MEMS陀螺仪作为一种新兴的角速率传感器,在当今社会的各个领域得到大量应用,例如:惯性导航、军事科技、汽车工业、工业医疗和消费电子等[1-2].市场上最常见的MEMS陀螺仪均是正交振动式陀螺,相比传统陀螺,其结构设计上以高频微幅振动的微型部件代替高速旋转的转子(如传统机械陀螺)和复杂昂贵的光路(如光纤陀螺和激光陀螺),基本工作原理都是产生并检测哥氏效应,即利用哥氏效应实现互相正交的驱动模态和敏感模态之间的能量转移.但由于微加工水平和微弱信号检测等技术限制,目前已研发成品的MEMS陀螺还未达到惯性级水平,仍属于中低精度的惯性器件;此外,加工制造和现场应用环境带来的参数不确定(如微米量级的尺度效应)和外界干扰(如基座震动)也是影响陀螺角速率检测精度的主要原因,亟需相关控制策略抑制不确定参数和外界干扰对系统的影响.
对常规的一轴驱动另一轴检测的操作模式,微弱信号检测[3]是影响MEMS陀螺精度的问题之一.为提高输出灵敏度,要求激励电压与驱动/敏感模态的自然振荡频率匹配.在这个问题的研究中,新颖的结构设计[4]和频率跟踪技术[5]得以大量应用,但同时额外的加工工艺和控制电路增加了陀螺的设计成本和调试难度.为此,Oropeza-Ramos[6]等人提出参数激励方法,该方法能有效减小正交耦合哥氏力带来的有害振荡,成为近几年的研究热点[7].在微弱信号处理方面,基于卡尔曼滤波和支持向量机的信号降噪和补偿技术也得到一定应用[8-9].
一轴驱动一轴检测的操作模式,尽管已有上述策略来提高陀螺的检测精度,但操作模式上的缺陷仍然无法避免:频率匹配需要额外的加工工艺或控制电路,不利于微型化和集成化;无法完全消除耦合哥氏力带来的额外震荡;只能用多个陀螺来实现多轴检测;无法实现角速率的实时在线估计[10].为此,Park[11]率先提出一种新的MEMS陀螺操作模式,将力反馈控制的思想应用在MEMS陀螺仪控制中:在驱动轴和敏感轴均施加反馈控制信号形成双闭环,使两个轴向的模态运动跟踪不同频率的正弦轨迹,同时应用自适应控制实现角速率的在线估计.由于该模式突破了角速率无法在线估计的限制,一经提出,自适应控制[12]、自抗扰控制[13]、H∞控制[14]、滑模控制[15-16]等控制方案迅速得到应用.此外该操作模式也弱化了驱动模态和检测模态的界限,为多轴MEMS陀螺仪提供了一种新的设计理念.在Park操作模式启发下,James[17]于2006年提出了一种单质量块三轴MEMS陀螺仪结构.在此后的研究中,为了降低滑模控制信号中抖振,学者Fei等人在滑模控制理论框架内提出了大量智能控制器,利用模糊逻辑[18-20]或神经网络[21-22]来逼近系统总的参数不确定和外界干扰,将鲁棒切换项的增益由总的不确定和干扰的上界变为其逼近误差的上界,大大减弱了控制信号的抖振,以更小的功耗实现三轴MEMS陀螺的轨迹跟踪和外界角速率的在线估计.在降抖研究中,另一种思路是根据干扰形式设计合适的干扰观测器[23-25],但在应用中大多是观测系统的匹配干扰.
尽管上述智能滑模控制器和干扰观测器在MEMS陀螺的轨迹跟踪和角速率估计方面表现出理想的效果,但对参数不确定和干扰的假设大都为匹配成分,即假设陀螺速度项精确可测,外界干扰可以完全等效作用到控制输入通道.而对陀螺中不匹配成分的抑制,文[16]采用的是传统的比例积分滑模面,且不匹配成分假设为高斯白噪声,而积分成分的引入使滑模面到达时间延长,无法实现系统降阶.本文针对速度测量存在常值误差而非高斯白噪声的MEMS陀螺,对Fei等文献中的陀螺模型作一步变换,采用一种新颖的比例微分滑模面和一阶非线性干扰观测器实现陀螺三轴不匹配干扰的在线估计补偿,获得足够小的鲁棒切换增益;同时设计一种带补偿因子的滑模控制器实现陀螺三轴轨迹的更快、更高精度跟踪,保证外界角速率的高精度测量.
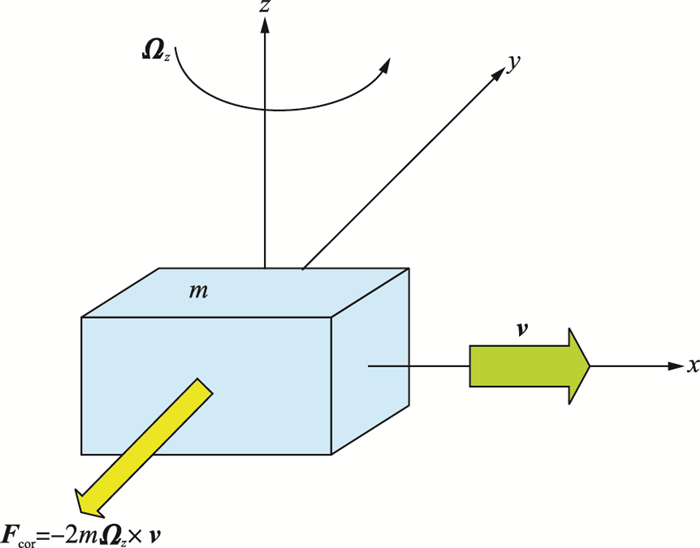
2 三轴MEMS陀螺建模正交振动MEMS陀螺是通过哥氏效应检测外界角速率.哥氏效应的原理如图 1所示:假定在x轴正方向施以速度v,若质量块m按图示方向以角速度Ωz绕z轴旋转,则在y轴负方向会产生大小为2mΩz×v的哥氏力Fcor.这样y轴负方向哥氏力的大小与z轴旋转角速率Ωz成正比,检测哥氏力的大小即可得到旋转角速率.
|
| 图 1 哥氏效应原理图 Figure 1 Schematic diagram of Coriolis effect |
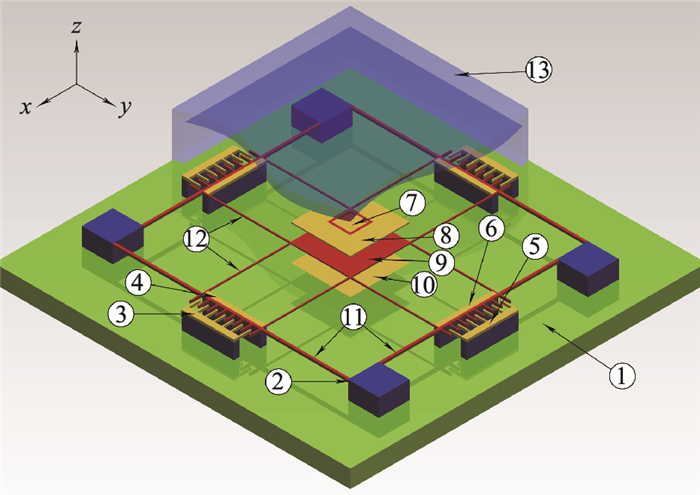
相比常见的单轴MEMS陀螺,文[13]所提的新颖结构在z轴方向分别设置驱动极板和敏感极板,如图 2所示.该结构仅用一个振动质量块即可检测3个轴向的角速率,可以大大减少占用空间,增加陀螺产量,降低成本和能耗,同时避免多质量块之间的机械干扰.
|
| 图 2 单质量块三轴MEMS陀螺仪结构图 Figure 2 Structure diagram of single-mass MEMS triaxial gyroscope ①基底 ②锚点 ③x轴固定静电驱动梳齿 ④x轴固定敏感电容极板 ⑤y轴固定静电驱动梳齿 ⑥y轴固定敏感电容极板 ⑦顶部z轴固定敏感电容极板 ⑧顶部z轴固定静电驱动极板 ⑨振动检测质量块 ⑩底部z轴固定静电驱动极板 ⑪外部折叠弹簧梁 ⑫内部折叠弹簧梁 ⑬封装 |
假设外界角速率为常值,考虑系统机械耦合并忽略离心力,三轴MEMS陀螺仪动态方程可以用式(1)所示的二阶线性常微分方程组表示[12]:
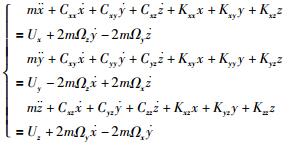
|
(1) |
其中,Ux、Uy、Uz表示3个轴向的控制力,Cxx、Cyy、Czz为三轴阻尼项,Kxx、Kyy、Kzz为三轴刚度项;假设机械耦合导致对称的阻尼项Cxy、Cxz、Cyz和刚度项Kxy、Kxz、Kyz;Ωx、Ωy、Ωz是3个轴向的外界角速率.
参考文[15-18],取无量纲时间t*=w0t(单位为l),参考长度q0(单位为m),参考频率w0(单位为Hz),对模型(1)进行无量纲化处理.以x轴为例,重新定义如下系数:
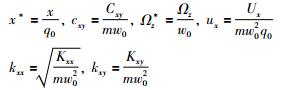
|
同理应用于y,z轴,得到最终的单质量块三轴MEMS陀螺仪无量纲化运动模型:
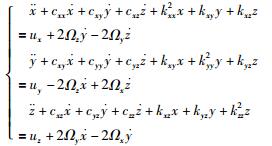
|
(2) |
将式(2)写成向量形式:
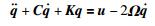
|
(3) |
其中
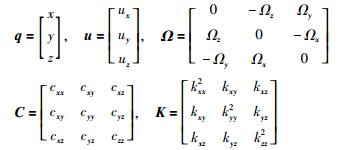
|
考虑Park操作模式,本文的控制目的为:设计控制律使得式(3)所示的MEMS陀螺的3个轴向运动跟踪指定的不同频率信号,同时在线估计补偿陀螺系统的不匹配干扰.
3 基于非线性干扰观测的滑模控制器设计不同于文[15-18]的状态方程,本文为控制器设计方便,将式(3)写成新的状态方程如下,其中系统参数以分块矩阵形式表达:
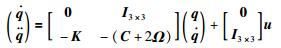
|
(4) |
考虑无法等效到控制输入通道的不匹配干扰fu=[fux fuy fuz]T及其参数阵Bu,新状态方程及其系统矩阵、输入矩阵定义为
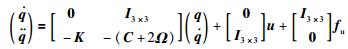
|
(5) |
其中,
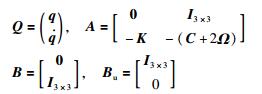
|
同理,将正弦参考轨迹:
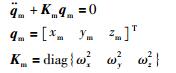
|
写成分块矩阵式的状态方程:
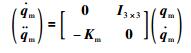
|
(6) |
其中,
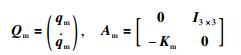
|
定义跟踪误差及误差动态:
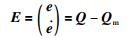
|
(7) |
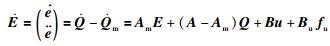
|
(8) |
不失一般性,假设三轴期望轨迹qm满足可跟踪条件,即存在常值矩阵M使得A+BMT=Am成立.则式(8)变为
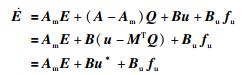
|
(9) |
其中,u*=u-MTQ为误差系统的等效输入.
一阶非线性干扰观测器(NPOB)设计如下:
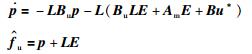
|
(10) |
其中,p是辅助变量,L=[diag{lx ly lz} 0]是观测器增益,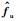
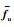
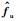
新滑模面设计为
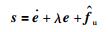
|
(11) |
其中,λ为待设计增益.为保证观测器收敛及滑模控制律设计方便,有如下假设:
假设1 不匹配干扰fui及其导数ḟui有界,且满足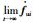
假设2 不匹配干扰的估计误差有界,即εi=sup|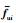
定理1 基于式(10)所示NPOB的滑模控制律设计如式(12)时,闭环误差系统(9)渐近稳定.
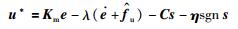
|
(12) |
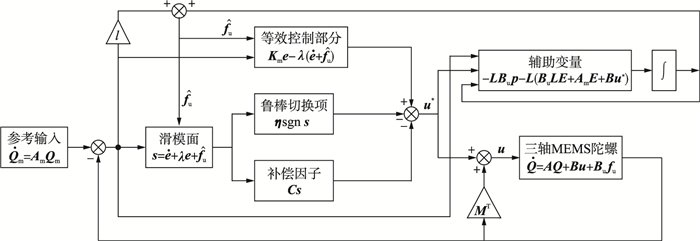
其中,Cs为设计的补偿因子,切换增益η=diag{ηx ηy ηz}满足ηi>(λ+li)εi且li>0.整个控制系统的结构框图如图 3所示.
|
| 图 3 基于非线性干扰观测器的滑模控制器结构图 Figure 3 The diagram of sliding mode controller based on nonlinear perturbation observer |
证明
(1) 滑模面可达性
为证明方便,令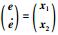
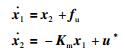
|
(13) |
取滑模面(11)的一阶微分:
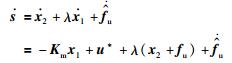
|
(14) |
将式(12)的控制律代入上式,得
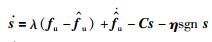
|
(15) |
对式(10)的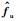
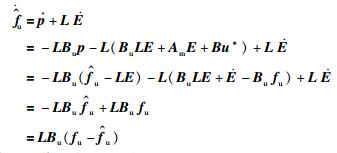
|
(16) |
式(16)代入式(15),得
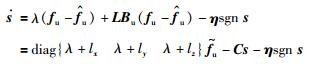
|
(17) |
对式(17)的滑模面动态取李亚普诺夫函数:
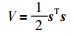
|
(18) |
上式对时间求导并将式(17)代入:
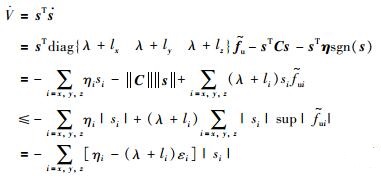
|
(19) |
通过选择ηi>(λ+li)εi,可以保证滑模面在有限时间收敛到0.而当s=0时,即:
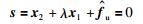
|
(20) |
结合式(13),则滑模运动变为
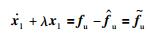
|
(21) |
式(21)表明,要使状态x1渐近收敛,需要证明干扰观测器的估计误差能够渐近收敛到0.同时需要说明的是,基于NPOB的滑模面上的运动只能保证状态x1(即位置跟踪误差e)渐近收敛,参考式(20),当x1=0时,x2=-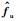
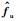
(2) 观测器估计误差的收敛性
式(16)的两边同时减ḟu,得
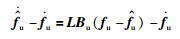
|
(22) |
参考观测器估计误差定义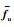
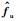
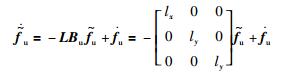
|
(23) |
考虑假设1中的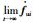
为了验证干扰观测器抑制不匹配干扰的有效性,利用Matlab/Simulink对整个陀螺闭环控制系统进行了仿真实验.假设三轴MEMS陀螺仪的已知参数如下[14-18]:
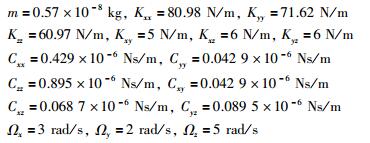
|
无量纲化过程中,参考长度取q0=10-6 m,参考频率取w0=3 kHz.假设3个轴向的参考轨迹为:
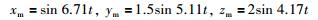
|
滑模面设计参数λ=40,NPOB的初值为0,增益为li=100,切换增益η=diag{5 5 5},补偿增益C=diag{50 50 50}.未知的不匹配干扰fu假设为
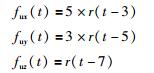
|
其中,r(t)表示阶跃函数.假设陀螺初始状态为Q(0)=0,仿真结果如图 4~图 8所示.
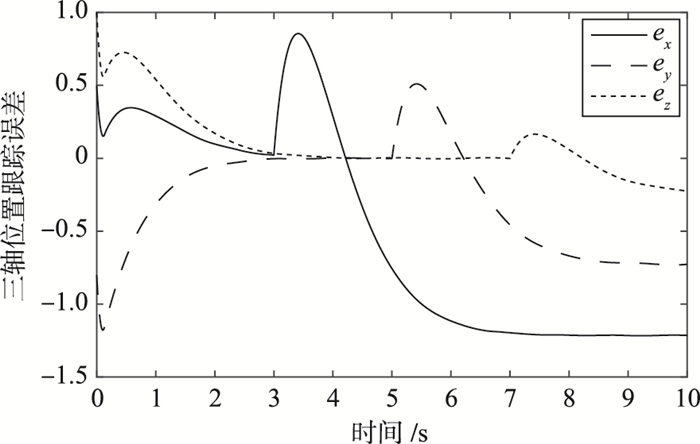
|
| 图 4 PI滑模面的三轴位置跟踪误差 Figure 4 Position tracking error of three axes with PI sliding mode |
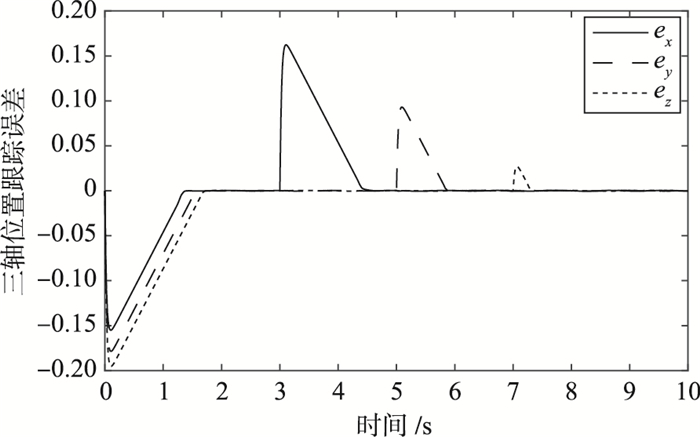
|
| 图 5 无补偿因子的三轴位置跟踪误差 Figure 5 Position tracking error of three axes without compensation factor |
|
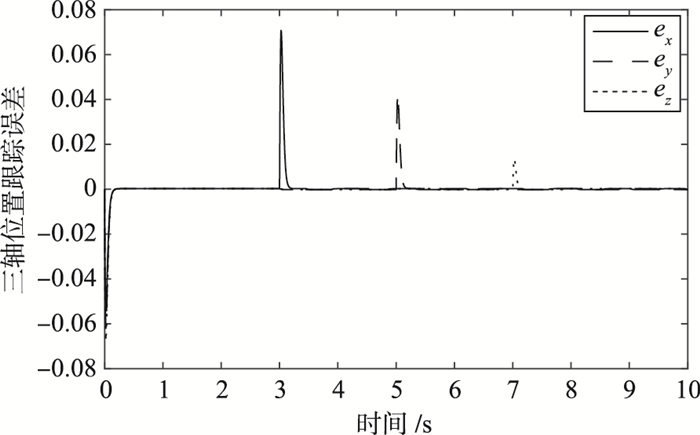
| 图 6 带补偿因子的三轴位置跟踪及跟踪误差 Figure 6 Position tracking and position tracking error of three axes with compensation factor |
|
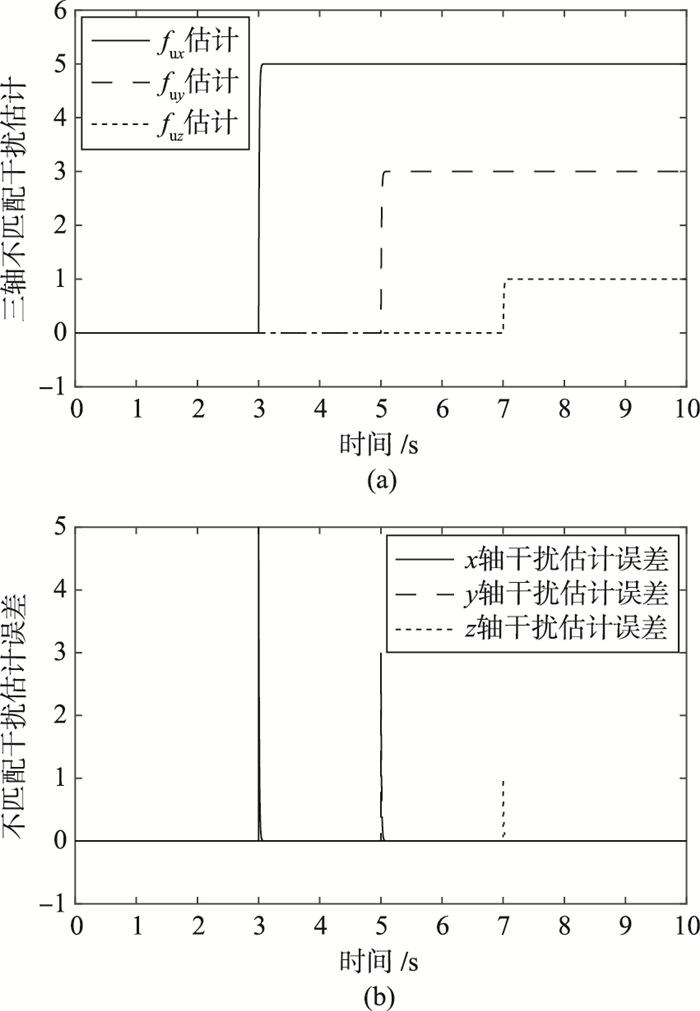
| 图 7 三轴不匹配干扰的估计及估计误差 Figure 7 The estimation and the estimation error of the unmatched perturbations in three axes |
|
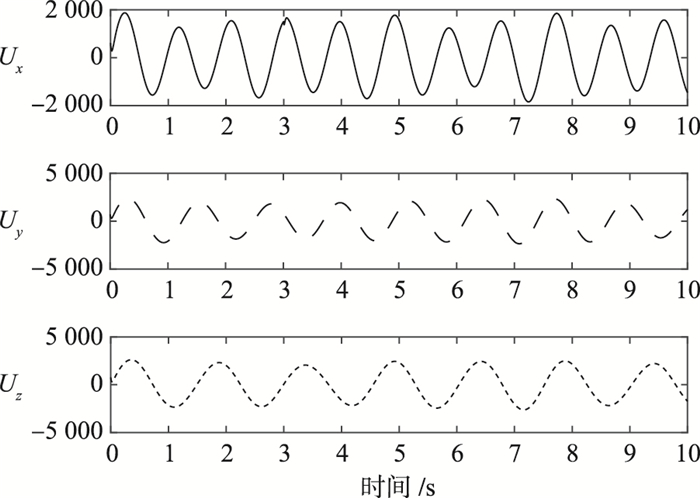
| 图 8 3个轴向的控制输入 Figure 8 Control inputs of three axes |
图 4表明常规的PI滑模面无法有效抑制常值不匹配干扰;而对比图 5、图 6可以表明基于非线性干扰观测器的滑模控制器可以使陀螺3个轴向的位置跟踪误差收敛到0,而带补偿因子的控制器可以使位置跟踪误差提高一个数量级(如x轴跟踪误差由0.16提高至0.07),而且收敛时间由1.8 s减少至0.2 s,表明补偿因子可以有效改善陀螺三轴的收敛特性.
图 7为不匹配干扰的实时估计结果.可以看出,所采用的非线性干扰观测器可以以较高精度实时重构系统的未知不匹配成分,重构的干扰通过反馈控制律作用于Park操作模式下的陀螺系统,补偿干扰的同时,使滑模控制律的切换增益取得足够小,无需额外的降抖手段抑制控制信号的微幅高频震荡.图 8为有界控制信号,可以看出该控制信号较为平稳,不存在常规滑模控制器中常见的剧烈抖振,方便系统执行器设计,也避免了高频抖振可能激发的系统未知动态.
5 结论本文针对Park操作模式下三轴MEMS陀螺的轴向轨迹跟踪控制问题,提出了一种基于非线性干扰观测器的滑模控制器,利用观测器实时估计补偿系统的不匹配扰动,同时降低滑模切换增益进而降低控制抖振.最后通过李亚普诺夫滑模面的可达性和观测器的收敛性.仿真结果表明,本文设计的控制器可以保证MEMS陀螺可以较好的跟踪指定的参考轨迹,方便角速率信号的检测.
| [1] | Shaeffer D K. MEMS inertial sensors:A tutorial overview[J]. IEEE Communications Magazine, 2013, 51(4): 100–109. DOI:10.1109/MCOM.2013.6495768 |
| [2] | Guo Z S, Cheng F C, Li B Y, et al. Research development of silicon MEMS gyroscopes:A review[J]. Microsystem Technologies, 2015, 21(8): 2053–2066. |
| [3] |
张云福, 吕梦琴, 罗亮, 等.
电容式微机械陀螺仪信号检测电路[J]. 传感技术学报, 2013, 26(6): 879–882.
Zhang Y F, Lv M Q, Luo L, et al. A readout circuit for capacitive vibratory micro-gyroscopes[J]. Chinese Journal of Sensors and Actuators, 2013, 26(6): 879–882. |
| [4] | Alper S E, Akin T. Symmetrical and decoupled nickel microgyroscope on insulating substrate[J]. Sensors and Actuators:A-Physical, 2004, 115(2/3): 336–350. |
| [5] |
罗兵, 王安成, 吴美平.
基于相位控制的硅微机械陀螺驱动控制技术[J]. 自动化学报, 2012, 38(2): 206–212.
Luo B, Wang A C, Wu M P. A drive control scheme based on phase-control for silicon micromechanical gyroscopes[J]. Acta Automatica Sinica, 2012, 38(2): 206–212. |
| [6] | Oropeza-Ramos L A, Turner K L. Parametric resonance amplification in a MEMS Gyroscope[C]//Proceedings of the Fourth IEEE Conference on Sensors. Piscatway, NJ, USA:IEEE, 2005:660-663. http://ieeexplore.ieee.org/document/1597785/ |
| [7] | Ali P, Hassan S. A parametric study on design of a microrate-gyroscope with parametric resonance[J]. Measurement, 2013, 46(8): 2661–2671. DOI:10.1016/j.measurement.2013.03.022 |
| [8] | Xue L, Jiang C Y, Chang H L, et al. A novel Kalman filter for combining outputs of MEMS gyroscope array[J]. Measurement, 2012, 45(4): 745–754. DOI:10.1016/j.measurement.2011.12.016 |
| [9] | Bhatt D, Aggarwal P, Bhattacharya P, et al. An enhanced MEMS error modeling approach based on nu-support vector regression[J]. Sensors, 2012, 12(7): 9448–9466. |
| [10] | Park S, Horowitz R. Adaptive control for the conventional mode of operation of MEMS gyroscopes[J]. Journal of Microelectromechanical Systems, 2003, 12(1): 101–108. DOI:10.1109/JMEMS.2002.807468 |
| [11] | Park S, Horowitz R. New adaptive mode of operation for MEMS gyroscopes[J]. Journal of Dynamic Systems Measurement and Control-Transactions of the ASME, 2004, 126(4): 800–810. DOI:10.1115/1.1849252 |
| [12] | Park S, Horowitz R, Tan C W. Dynamics and control of a MEMS angle measuring gyroscope[J]. Sensors and Actuators:A-Physical, 2008, 144(1): 56–63. DOI:10.1016/j.sna.2007.12.033 |
| [13] | Zheng Q, Dong L L, Lee D H, et al. Active disturbance rejection control for MEMS gyroscopes[J]. IEEE Transactions on Control Systems Technology, 2009, 17(6): 1432–1438. DOI:10.1109/TCST.2008.2008638 |
| [14] | Li W L, Liu P X. Adaptive tracking control of an MEMS gyroscope with H-infinity performance[J]. Journal of Control Theory and Applications, 9(2):237-243. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=kzll201102017&dbname=CJFD&dbcode=CJFQ |
| [15] | Batur C, Sreeramreddy T, Khasawneh Q. Sliding mode control of a simulated MEMS gyroscope[J]. ISA Transactions, 2006, 45(1): 99–108. DOI:10.1016/S0019-0578(07)60069-X |
| [16] | Fei J T, Batur C. A novel adaptive sliding mode control with application to MEMS gyroscope[J]. ISA Transactions, 2009, 48(1): 73–78. DOI:10.1016/j.isatra.2008.10.008 |
| [17] | James D J, Thurai V. Novel concept of a single mass adaptively controlled triaxial angular rate sensor[J]. IEEE Sensors Journal, 2006, 6(3): 588–595. DOI:10.1109/JSEN.2006.874458 |
| [18] | Wang S T, Fei J T. Robust adaptive sliding mode control of MEMS gyroscope using T-S fuzzy model[J]. Nonlinear Dynamics, 2014, 77(1/2): 361–371. |
| [19] | Fang Y M, Yuan Z L, Fei J T. Adaptive fuzzy backstepping control of MEMS gyroscope using dynamic sliding mode approach[J]. Information Technology and Control, 2015, 44(4): 380–386. |
| [20] | Lei D D, Wang T T, Cao D, et al. Adaptive dynamic surface control of MEMS gyroscope sensor using fuzzy compensator[J]. IEEE Access, 2016(4): 4148–4154. |
| [21] | Fei J T, Yang Y Z. Robust neural network control of MEMS gyroscope using adaptive sliding mode compensator[J]. Robotica, 2016, 34: 497–512. DOI:10.1017/S026357471400160X |
| [22] | Wu D, Fei J T. Adaptive neural sliding control of MEMS gyroscope with robust feedback compensator[J]. Transactions of the Institute of Measurement and Control, 2016, 38(4): 414–424. DOI:10.1177/0142331215585879 |
| [23] |
麻颖俊, 郭洪艳, 陈虹, 等.
基于滑模观测器的汽车轮胎力级联估计方法[J]. 信息与控制, 2016, 45(2): 177–184.
Ma Y J, Guo H Y, Chen H, et al. Cascade tire-force estimation method based on sliding-mode observer[J]. Information and Control, 2016, 45(2): 177–184. |
| [24] |
肖松, 吴云洁, 刘晓东.
基于干扰观测器的飞行仿真转台全局滑模控制方法[J]. 信息与控制, 2014, 43(4): 411–416.
Xiao S, Wu Y J, Liu X D. Global sliding mode control method for a flight simulator based on disturbance observer[J]. Information and Control, 2014, 43(4): 411–416. |
| [25] |
王伟, 赵清, 吕晓永, 等.
三轴微机电系统陀螺仪自适应干扰补偿方法[J]. 控制理论与应用, 2014, 31(4): 451–457.
Wang W, Zhao Q, Lv X Y, et al. Adaptive perturbation compensation for micro-electro-mechanical systems tri-axial gyroscope[J]. Control Theory&Applications, 2014, 31(4): 451–457. |



