2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
0 引言
随着装备与技术的迅猛发展,无人机以其独特的作战优势占据了高科技信息化战争的一个制高点,正在推动一场空中侦察和作战的革命[1-3].无人机的发展受到越来越多国家的高度重视,无人机的使用范围也已拓展至军事、民用和科研三大领域.在军事领域,可以预言,无人机将在未来的战争或局部冲突中显示出更为强大的威力,成为未来"零伤亡"战争形式的首选武器之一.
在执行战场侦察任务的过程中,对战场动态目标的捕获跟踪能力对于无人机而言不可或缺.计算机视觉是利用计算机系统实现类似人类视觉系统理解客观世界的新兴学科,逐渐成为人工智能和信息科学研究的热点领域之一.计算机科学、电子技术和机器学习等多学科的飞速发展,有效地解决了视觉技术中运算速度低下、存储容量有限等问题,将机器视觉技术应用于无人机目标跟踪领域正在受到越来越多的重视.法国贡比涅科技大学的Kendoul等[4]采用光流技术进行小型无人机的3D自主定位,在导航的过程中完成场景地图的搭建工作. Lin等[5]设计了一种实时嵌入式视觉系统,安装于无人旋翼机上用于地面目标跟踪,该方法可以较为鲁棒地工作.澳大利亚阿德莱德大学的Singh等[6]则探究了无人机海洋视觉伺服系统在进行目标检测跟踪中的可行性,并在其中采用了Meanshift跟踪方法进行验证.
无人机利用计算机视觉进行目标跟踪的目的在于确定目标的位置,一般通过状态估计的方法进行视觉跟踪的策略主要包括卡尔曼滤波(Kalman filter,KF)[7]、扩展卡尔曼滤波(extended Kalman filter,EKF)[8]和粒子滤波(particle filter,PF)[9].其中粒子滤波基于Montecarlo思想和递推贝叶斯估计,适用于非高斯噪声环境和非线性的情况,近年来在国内外的机器人定位、导航和跟踪等研究领域中受到极大关注[10].但常规的粒子滤波方法存在着重采样过程中粒子贫化的问题,并且由于该方法的出发点是用事件的频率来近似其概率,因此需要大量粒子逼近,计算效率较低.针对粒子滤波的各种问题,近年来国内外提出了大量改进的方案. Kim等[11]提出了基于l1正则学习模型的时空辅助粒子滤波方法,避免了由于目标突然的动态变化而产生的漂移问题.国防科技大学的强波等[12]提出了一种基于无迹粒子滤波器学习基因调控网络参数的方法,通过对Repressillar模型中隐变量与未知参数的估计,有效地减少了估计误差. Ding等[13]则从特征提取角度出发,融合了图像颜色和纹理两类特征,从而克服粒子滤波跟踪过程中所带来的目标非线性移动、遮蔽和亮度变化的影响.
群智能算法是一类先进的仿生智能优化算法,近十几年以来已经在包括计算机视觉在内的多个研究领域取得广泛应用[14-17].包括遗传算法、粒子群算法、蜂群算法和生物地理学算法在内的多种仿生智能优化方法,都是受生物群体的智能行为启发而提出的[18].受蝙蝠在飞行过程中利用所发出的超声波进行回声定位的机理启发,Yang[19]于2010年提出了新型的元启发式群智能算法——蝙蝠算法(bat-inspired algorithm),该算法本质上可以视为粒子群优化和强局部搜索过程的有机结合,而粒子群算法和和声算法则可以看作蝙蝠算法进行某种程度简化之后的特殊情况,因此蝙蝠优化算法可以在更广阔的领域内发挥其更大的潜能.
本文在原有的蝙蝠优化算法中加入混沌变异策略,改进算法的搜索能力,并将其应用于无人机侦察任务中的基于粒子滤波的目标跟踪中.在执行重采样之前进行蝙蝠优化搜索,可以避免重采样本身的粒子贫化现象.
1 基于混沌变异蝙蝠优化算法 1.1 蝙蝠优化算法(BA)蝙蝠不仅是唯一长有翅膀的哺乳动物,并且有强大的回声定位能力.受这种回声定位能力的启发,Yang等研究提出了一种蝙蝠启发式搜索优化算法.与其它群智能优化算法类似,蝙蝠优化算法在进行生物行为的模拟推演中采用了下述理想化法则[20]:
1) 全部的蝙蝠都采用回声定位方法感知距离和周围环境信息.
2) 在xi位置,蝙蝠随机飞行并具备某些性质,如速度为vi,频率为f,所发出的回声波长为λ,回声的响度为A0.回声的波长(频率)能够根据情况进行自适应的调节.依据蝙蝠自身和目标之间的距离,每只蝙蝠发出回声波脉冲的频率r在[0, 1]之间变化.此外,回声波响度在最小值Amin和某个更大的值A0之间变化.
本算法在进行生物行为模拟和数学模型构建时也进行了一些简化,如并未考虑3D拓扑和回波传输的时间延迟,这是因为当解决多维优化问题时,这些因素会大大地增加计算的复杂度.高频率的声波具有较短波长且传输距离相对更短,该算法将频率范围限定在[0,fmax],发出回声脉冲的频率则定在[0, 1].
每一只蝙蝠个体由其所处位置xi、速度vi、回声频率fi、回声响度Ai和发射回声脉冲的频率ri所定义.当频率为fi、时间(迭代代数)为t时,根据式(1)~式(3)对新解xit和vit进行更新:
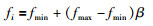
|
(1) |
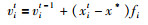
|
(2) |
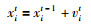
|
(3) |
其中,β∈[0, 1],x*是经由比较所有蝙蝠所在方位之后所得到的当前最佳位置(当前最优解).
蝙蝠优化算法在局部搜索环节采用了随机游走(random walk)操作,一旦选择某个解为最优解,每只蝙蝠个体所产生的新解为
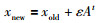
|
(4) |
其中,xold为蝙蝠个体旧解,ε∈[-1, 1]为随机尺度因子,At为在t代全部蝙蝠个体的平均响度值.
事实上,蝙蝠个体位置和速度的更新策略与其它群智能优化算法存在一些相似之处.在蝙蝠优化算法中,fi控制步长和群体的移动范围.该算法可以视为传统粒子群算法和强局部搜索策略的融合和平衡过程.
1.2 混沌变异的蝙蝠优化算法(CMBA)本文将混沌理论和相应的变异算子加入蝙蝠优化算法,对其搜索能力进行改进.混沌理论发端于Lorenz所描述的所谓蝴蝶效应.混沌序列通过方程xn+1=4xn(1-xn)映射计算得到,其中xn∈[0, 1].混沌理论的基本性质即在于初始状态的一个细微差异,经由长时间的演化后可以产生较大的影响.因此,混沌变量的遍历性和不规则性可以被用来进行当前最优解邻域的混沌搜索,从而帮助算法跳出局部最优,寻到最优的参数.
此外,为了提高蝙蝠算法的搜索效率并加速收敛,本文采用了微分进化算法中的变异算子,提高群体的多样性.当将某个解通过局部搜索,选择为当前最优解时,根据随机产生的数字rd来选择下一步更新的策略.若rd > ri,则利用随机游走算子对每只蝙蝠个体产生新的解;反之,则利用变异算子进行更新,如式(5)所示:
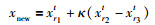
|
(5) |
其中,κ为变异权重因子,本文中κ=0. 5;r1、r2和r3为服从均匀分布的随机整数,大小在1和蝙蝠群体总数N之间.为了简化,在本文的仿真实验中,回声响度A和脉冲频率r选取固定值,A0=0. 5,r0=0. 5.
2 基于混沌变异蝙蝠优化的粒子滤波跟踪 2.1 粒子滤波粒子滤波方法由Gordon等提出,与传统滤波方法相比,它具有适用于非线性、简单易行等优点,因此被广泛应用于包括导航定位、故障诊断、汽车防撞和目标跟踪等诸多工业领域.
粒子滤波方法源于蒙特卡洛思想,即以某事件出现的频率来指代该事件的概率.具体而言,粒子滤波通过寻找一组在状态空间中随机传播的样本来近似概率密度函数p(xk,zk),这些样本被称为"粒子".用粒子均值来替代积分运算,获得状态的最小方差估计,从而完成优化搜索.采用这一方法,可以在滤波过程中处理任意形式的概率,而不像卡尔曼滤波那样只能处理高斯分布的概率模型,并在一定程度上解决了粒子数样本匮乏的问题.
设粒子样本集合为{st(n),wt(n)},其中st(n)是从重要性分布函数q(Xt|Xt-1,Yt)中采样得到的样本,wt(n)为其权值.对p(Xt|Y0: t)的估计过程大致分为预测、更新和重采样三个步骤:
Step 1 预测.当(t-1)时刻的后验概率p(xt-1|z0: t-1)已知时,根据全概率公式,可以对t时刻的先验概率密度函数进行预测:
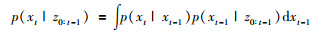
|
(6) |
Step 2 由贝叶斯公式,在t时刻得到观测值,并更新先验概率密度:
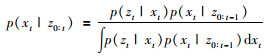
|
(7) |
Step 3 重采样.对N个样本及其权值wt(n)进行采样,得到新样本,从而增强权值较大的样本,抑制权值较小的样本.
2.2 基于混沌变异蝙蝠优化的粒子滤波跟踪目标的灰度分布描述是一种较为稳健的目标描述方法,能够一定程度上减弱变形、旋转等对跟踪性能的影响.本文选用灰度分布进行目标的描述,建立系统观测模型.设无人机战场侦察目标区域(即跟踪区域)的中心为X =(x,y),区域尺寸为h =(hx,hy),跟踪区域内像素位置设为Xi=(xi,yi),由此进行核概率密度估计进行目标的灰度分布描述.假设目标灰度分布离散化为B个bin,定义灰度量化函数b(Xi):R2→{1,…,B}表示把位置Xi处的像素灰度量化并分配到相应的bin中,这里B表示灰度的量化等级,由此定义目标的灰度分布为
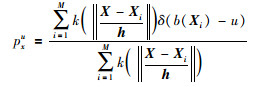
|
(8) |
其中,δ(·)为Kronecker Delta函数;跟踪区域内的像素总数记为M,k(·)为所采用的高斯核函数.
基本粒子滤波算法在重要性采样的过程中,粒子样本容易出现贫化问题,导致算法性能大大降低.本文引入蝙蝠优化算法优化粒子滤波的重要性采样过程,使得粒子群体在权重值更新前,更加趋向于高似然的区域,从而对粒子贫化的问题加以解决.首先设蝙蝠优化算法的适应值计算函数:
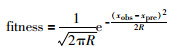
|
(9) |
其中,xobs为最新观测结果,xpre为预测值,R为观测噪声方差.
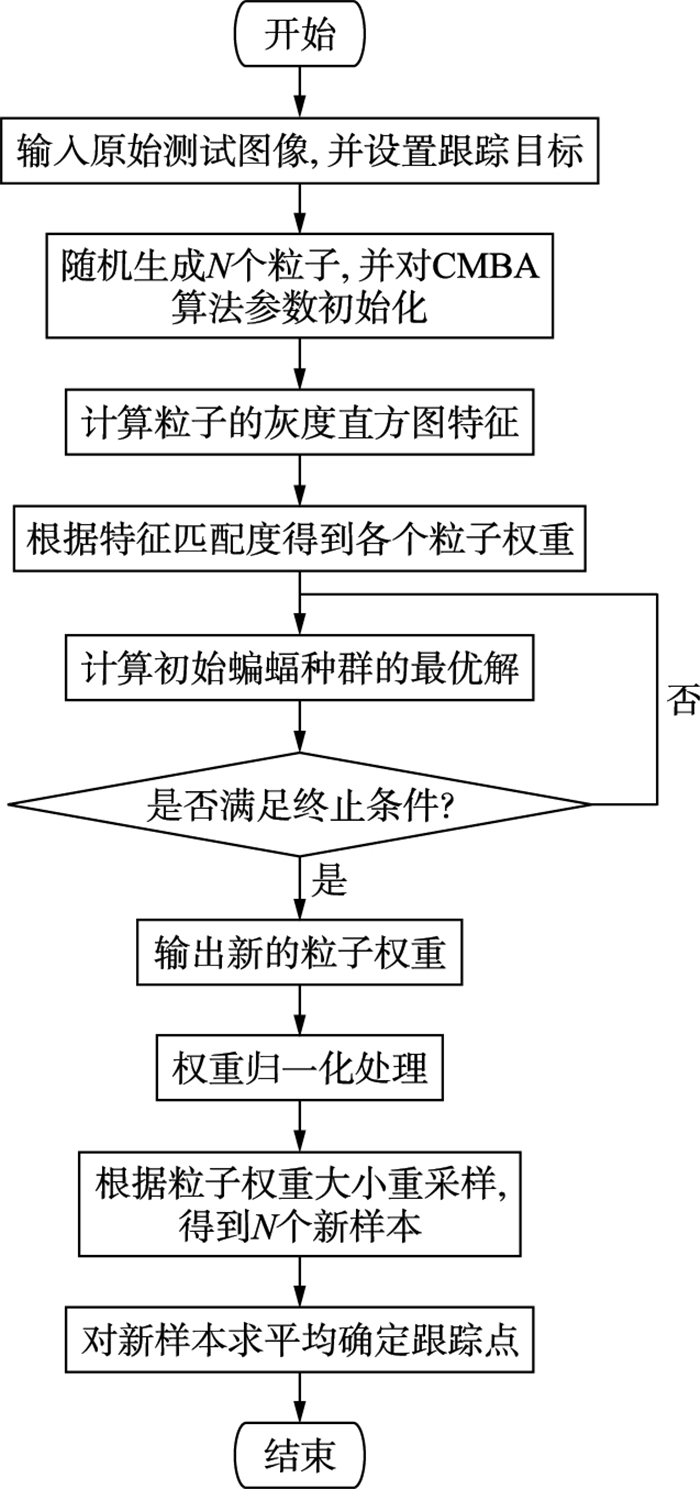
综上,基于蝙蝠优化机制改进的粒子滤波目标跟踪算法(Particle Filter tracking based on CMBA,CMBA-PF)流程如图 1所示.
|
| 图 1 CMBA-PF算法流程 Figure 1 Flow chart of the CMBA-PF algorithm |
在粒子重采样之后获取新样本,通过求平均确定跟踪点的过程演示如图 2所示,其中浅色点表示经过蝙蝠优化和重采样之后获得的新样本在图像中对应点,深色点为最终所确定的跟踪点.

|
| 图 2 确定跟踪点示意图 Figure 2 Schematic diagram of the tracking point determination |
为了测试本研究算法的性能,本文在多个测试视频上进行了对比实验.
本文方法实现于Windows操作系统,采用MATLAB 2012b作为编程平台,计算机CPU为Inter(R) Core(TM) 3. 2 GHz 4. 0 GB.软件操作界面如图 3所示.
|
| 图 3 Matlab软件操作界面 Figure 3 Operating interface of the Matlab |
首先针对混沌变异蝙蝠算法(CMBA)的优化性能,采用较常用的评价函数进行评价,并与普通蝙蝠优化算法进行了对比,对比结果如图 3所示.为了确保两种算法的可比性,对两者设置了相同的迭代次数,并对两者共有的参数设定了相同的初值,具体如表 1所示.
| 参数 | 取值 |
| 种群大小 | 20 |
| 最大进化代数 | 500 |
| 速度区间 | [-2, 2] |
| 初始响度 | A0=0.5 |
| 频率范围 | [0, 2] |
| 初始脉冲发射频率 | r0=0.5 |
表 2为4个测试所用的目标函数及其变量取值区间,其中除了f4(x)之外属于单模函数之外,其余3个都是多峰函数,存在多个极小值,较难优化,因此常用于进行算法优化性能的测试.
| 测试函数 | 搜索空间 |
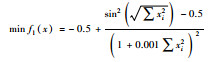
|
xi∈[-4, 4] |
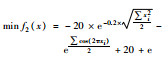
|
xi∈[-32, 32] |
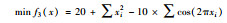
|
xi∈[-5, 5] |
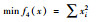
|
xi∈[-32, 32] |
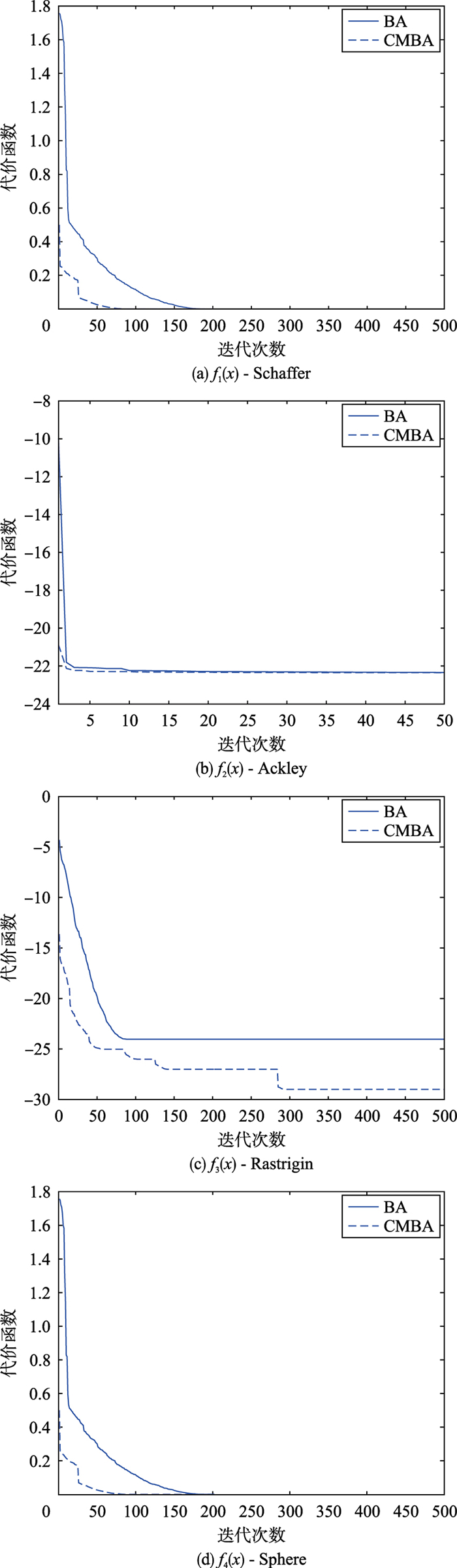
对比图 4的测试结果不难发现,CMBA在寻优精度上具有较大优势,尤其是当求解f1(x)、f3(x)和f4(x)时,CMBA在寻优精度上具有特别明显的优势,在收敛速度和所达到的最优值方面均优于基本蝙蝠算法的计算结果.
|
| 图 4 目标函数随循环次数的变化曲线 Figure 4 Changing curve of the objective function value |
在上文进行测试函数优化效果比较的基础上,本文采用无人机视角拍摄的视频作为观测输入,对场景中的运动目标进行了跟踪仿真.实验分为3组:第1组实验共选取220帧图像,图像尺寸为320×240;第2组共选取40帧图像,图像尺寸为640×272;第3组共选取200帧图像,图像尺寸为512×256.粒子滤波的相关参数设定为:粒子数量N=20.
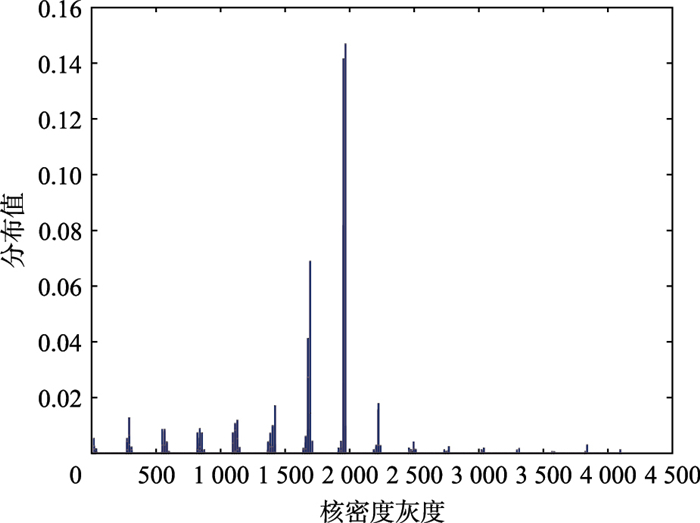
粒子的初始化方法为从上一帧跟踪点附近随机生成若干位置,目标模板和各个粒子对应的候选区域的核密度灰度分布直方图特征都从RGB空间转化到16×16×16维的向量.以场景1的模板为例,所生成的特征向量统计直方图表示如图 5所示.随后,根据每个粒子核密度灰度分布直方图特征向量与目标模板的相应特征向量进行匹配度计算,根据匹配度值的大小确定各个粒子的权重值.以上即粒子滤波的预测和修正过程.
|
| 图 5 核密度灰度分布特征直方图表示 Figure 5 Representation of the grey level probability density feature histogram |
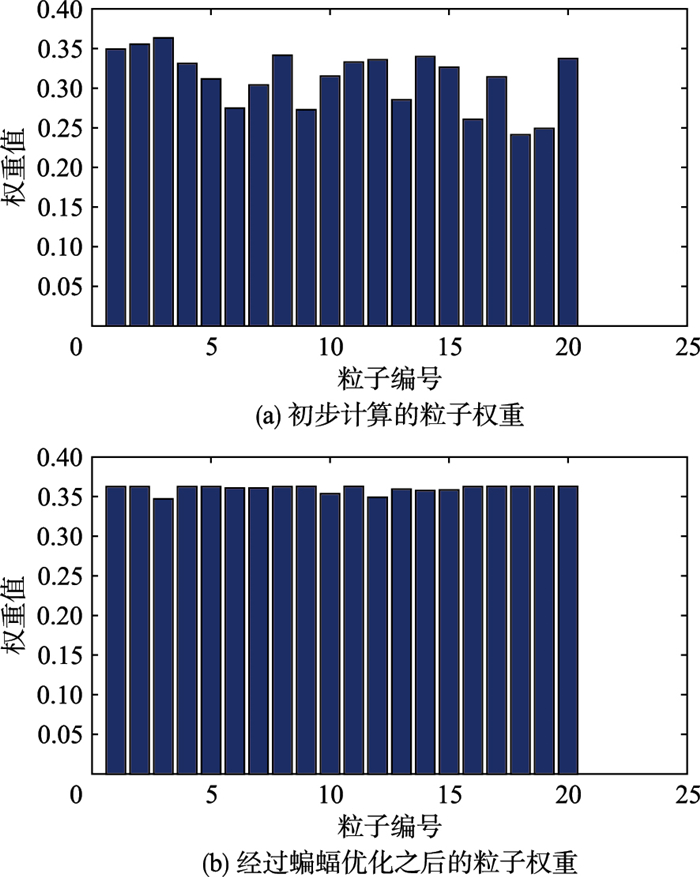
本文采用CMBA对粒子群体进行优化,使得所得到的新粒子趋向于更加高似然的区域,所获得的权重值相应增大.粒子在优化前后的权重值如图 6所示,其中柱状图代表各个粒子的权重值.由图 6可见,经过CMBA优化之后,粒子的权重整体上明显增大,对应位置的特征匹配度也就更高了.
|
| 图 6 粒子权重CMBA优化前后的数值仿真 Figure 6 Weight values of the particles before and after the CMBA optimization |
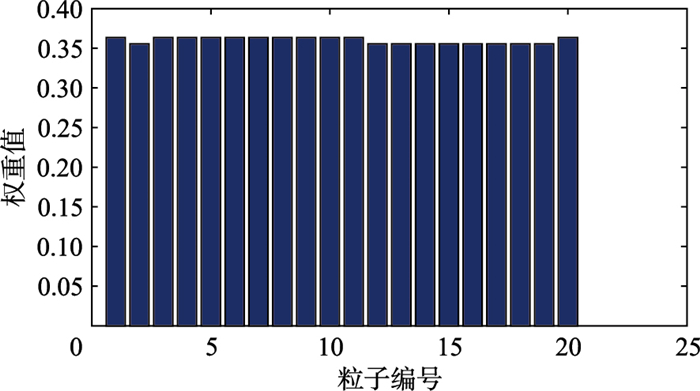
进行CMBA优化之后获得的粒子需通过重采样,将较高权重的粒子保留,同时剔除权重较低的粒子,重采样之后所得到的粒子权重如图 7所示,可见低权重的粒子已经排除.在确定跟踪点的过程中,粒子滤波通过重要性采样确定跟踪点,将权重较高的粒子求平均值来计算最终的跟踪结果,以后面的场景3为例,相应的演示验证如图 8所示,其中蓝色实心点代表重要性采样之后高权值粒子的分布位置,红色星号点为高权值粒子求平均所确定的跟踪位置.
|
| 图 7 重采样之后的粒子权重 Figure 7 Weight values of the important sampled particles |

|
| 图 8 粒子求平均演示验证 Figure 8 Illustration of the particle averaging |
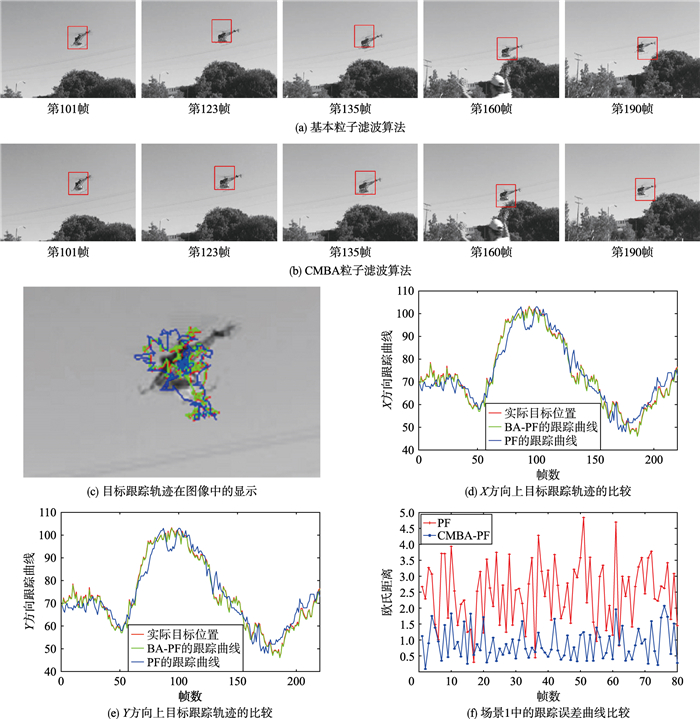
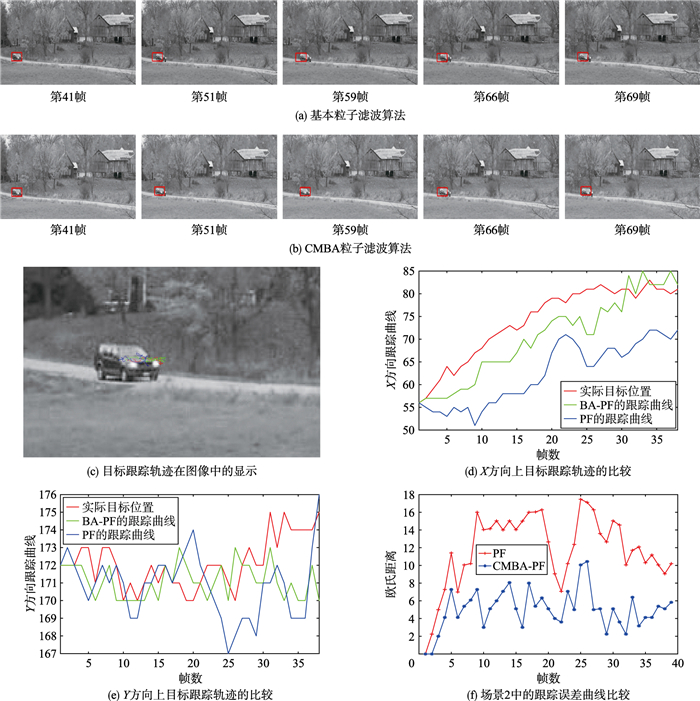
对3个不同场景的跟踪结果如图 9~图 11所示,其中红色线代表目标的真实运动轨迹,蓝色线代表采用标准粒子滤波的跟踪轨迹,绿色线表示采用蝙蝠算法优化的粒子滤波的跟踪轨迹,跟踪误差值的计算采用了粒子滤波跟踪点与真实数据之间的欧氏距离来进行判定.
|
| 图 9 仿真测试1跟踪结果 Figure 9 Tracking results in Scene 1 |
|
| 图 10 仿真测试2跟踪结果 Figure 10 Tracking results in Scene 2 |
|
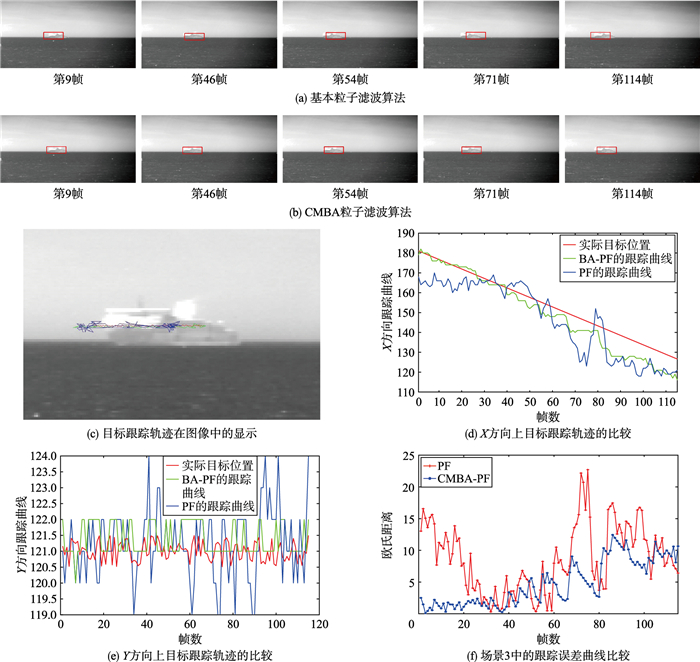
| 图 11 仿真测试3跟踪结果 Figure 11 Tracking results in Scene 3 |
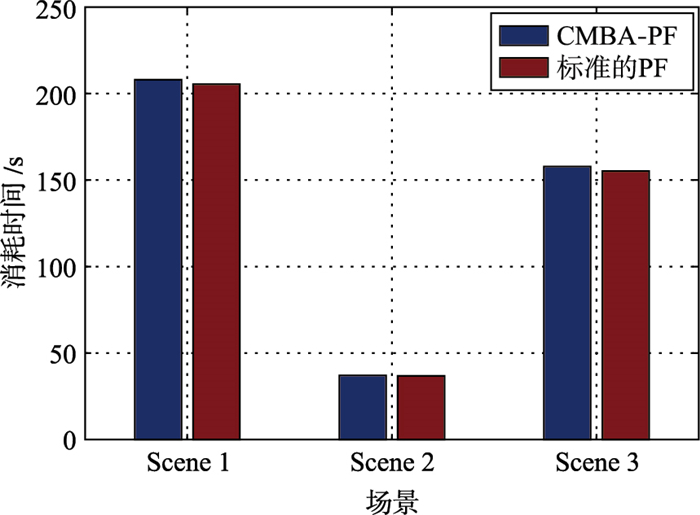
由图 9的场景1的仿真结果可以看出,当无人机视野中的目标因运动而发生一定程度的形变时,基本粒子滤波算法跟踪精度产生了明显的下降,而经由混沌变异蝙蝠算法优化的粒子滤波算法仍可保证该场景下的跟踪精度. 图 10的场景2对汽车目标进行跟踪,由跟踪误差曲线可知基于CMBA优化后的粒子滤波跟踪精度始终大于基本粒子滤波.在图 11的场景3中,船目标与天空背景之间的灰度反差较小,其中船上半部分较亮,与背景的灰度均值之差为30,下半部分较暗,与背景的灰度均值之差为28.采用基本粒子滤波的方案在数帧之后,跟踪点即发生一定程度的漂移.而利用CMBA算法寻优之后,这种漂移的影响即得到了很大程度的缓解.此外,图 12中对CMBA优化的粒子滤波(CMBA-PF)与标准的粒子滤波算法执行时间进行了对比,从3个场景来看,在跟踪精度有明显提升的前提下,CMBA-PF仅比标准的粒子滤波算法消耗时间高出很小的数值.综合来看,本文所设计的基于蝙蝠回波定位机制优化的粒子滤波跟踪性能与传统粒子滤波相比,有了明显的提升.
|
| 图 12 两种算法消耗时间对比 Figure 12 Time cost comparison between the two algorithms |
本文提出了一种基于蝙蝠优化算法的粒子滤波跟踪方法.引入蝙蝠优化算法优化粒子滤波的重采样过程,提高了跟踪算法的跟踪性能.测试视频的实验结果表明,本文方法在复杂背景下的跟踪具有较好的鲁棒性和准确性.在后面的工作中,将针对其它信号源图像的目标跟踪问题进行深入研究,对跟踪过程中的模板更新、目标遮挡等问题做进一步优化,并真正在无人机系统平台上进行算法的验证.
| [1] | Deng Y M, Duan H B. Biological edge detection for UCAV via improved artificial bee colony and visual attention[J]. Aircraft Engineering and Aerospace Technology, 2014, 86(2): 138–146. DOI:10.1108/AEAT-10-2012-0164 |
| [2] | Bertuccelli L F, Cummings M L. Operator choice modeling for collaborative UAV visual search tasks[J]. IEEE Transcations on System, Man, and Cybernetics-Part A:Systems and Humans, 2010, 42(5): 1088–1099. |
| [3] | Yang L, Pan Q, Zhang Y, et al. Simultaneously multi-UAV mapping and control with visual servoing[C]//International Conference on Unmanned Aircraft Systems. Piscataway, NJ, USA: IEEE, 2015: 125-131. |
| [4] | Kendoul F, Fantoni I, Nonami K. Optic flow-based vision system for autonomous 3D localization and control of small aerial vehicles[J]. Robotics and Autonomous Systems, 2009, 43(5): 591–602. |
| [5] | Lin F, Dong X X, Chen B M, et al. A robust real-time embedded vision system on an unmanned rotorcraft for ground target following[J]. IEEE Transactions on Industrial Electronics, 2012, 59(2): 1038–1049. DOI:10.1109/TIE.2011.2161248 |
| [6] | Singh G, Anvar A. Investigating feasibility of target detection by visual servoing using UAV for oceanic applications[C]//International Conference on Control Automation Robotics & Vision. Piscataway, NJ, USA: IEEE, 2015: 1621-1626. |
| [7] | Ding Q, Zhao X, Han J. Adaptive unscented Kalman filters applied to visual tracking[C]//International Conference on Information and Automation. Piscataway, NJ, USA: IEEE, 2011: 491-496. |
| [8] | Zhou J. EKF based object detect and tracking for UAV by using visual-attention-model[C]//International Conference on Progress in Informatics and Computing. Piscataway, NJ, USA: IEEE, 2014: 168-172. |
| [9] | Arulampalam S, Maskell S, Gordon N. A tutorial on particle filters for online non-Gaussian Bayesian tracking[J]. IEEE Transactions on Signal Processing, 2002, 50(2): 138–146. |
| [10] | Katayama K, Shibata K, Horita Y. Detection and tracking an object in omni-directional images using particle filter[C]//SICE Conference. Piscataway, NJ, USA: IEEE, 2012: 1040-1043. |
| [11] | Kim Y D, Jeon M. Spatio-temporal auxiliary particle filtering with l1-norm-based appearance model learning for robust visual tracking[J]. IEEE Transactions on Image Processing, 2013, 22(2): 511–522. DOI:10.1109/TIP.2012.2218824 |
| [12] |
强波, 王正志, 倪青山.
面向调控网络参数学习的无迹粒子滤波算法[J]. 计算机工程与应用, 2011, 47(9): 146–148.
Qiang B, Wang Z Z, Ni Q S. Estimating parameters in gene regulatory network oriented unscented particle filter[J]. Computer Engineering and Applications, 2011, 47(9): 146–148. |
| [13] | Ding D, Jiang Z, Liu C. Object tracking algorithm based on particle filter with color and texture feature[C]//Control Conference. Piscataway, NJ, USA: IEEE, 2016: 4031-4036. |
| [14] |
肖红, 李盼池.
改进的量子行为粒子群优化算法及其应用[J]. 信息与控制, 2016, 45(2): 157–164.
Xiao H, Li P C. Improved Quantum-behaved Particle Swarm Optimization Algorithm and Its Application[J]. Information and Control, 2016, 45(2): 157–164. |
| [15] | Gao M L, He X H, Luo D S, et al. Object tracking using firefly algorithm[J]. IET Computer Vision, 2013, 7(4): 227–237. DOI:10.1049/iet-cvi.2012.0207 |
| [16] | Musa Z, Salleh M Z, Bakar R A, et al. GbLN-PSO and model-based particle filter approach for tracking human movements in large view cases[J]. IEEE Transactions on Circuits & Systems for Video Technology, 2015, 26(8): 1433–1446. |
| [17] |
朱云龙, 申海, 陈瀚宁, 等.
生物启发计算研究现状与发展趋势[J]. 信息与控制, 2016, 45(5): 600–614.
Zhu Y L, Shen H, Chen H N, et al. Research Status and Development Trends of the Bio-inspired Computation[J]. Information and Control, 2016, 45(5): 600–614. |
| [18] |
张晓茹, 张著洪.
求解多模态函数优化的微果蝇优化算法[J]. 信息与控制, 2016, 45(3): 361–370.
Zhang X R, Zhang Z H. Micro Fly Optimization Algorithm Solving Multi-modal Function Optimization[J]. Information and Control, 2016, 45(3): 361–370. |
| [19] | Yang X. A new metaheuristic bat-inspired algorithm[J]. Nature Inspired Cooperative Strategies for Optimization, 2010, 284: 65–74. DOI:10.1007/978-3-642-12538-6 |
| [20] |
徐华, 张庭, 包哲人, 等.
求解柔性作业车间调度问题的改进蝙蝠算法[J]. 信息与控制, 2016, 45(6): 722–728.
Xu H, Zhang T, Bao Z R, et al. Improved Bat Algorithm for Solving Flexible Job-shop Scheduling Problems[J]. Information and Control, 2016, 45(6): 722–728. |



