0 引言
近年来技术发展、创新刺激了四旋翼无人机在社会经济各领域的应用,如火灾救援[1]、农业服务[2]、电力巡检[3]、警方执法[4]、航拍摄影[5]等.如今已有多种控制方法运用于四旋翼无人机的动态控制,如PID[6]、LQR[7]、鲁棒控制[8]、反演控制[9]、滑模控制[10]、反馈线性化[11]、自适应控制[12]等.近些年有学者对模型预测控制策略在旋翼无人机飞控上的应用进行了研究:天津大学孙秀云等[13]针对四旋翼飞行器偏航通道设计了一种基于MPC的控制器,具有抵抗阵风干扰的强鲁棒性.外国学者Mujtaba等[14]提出了一种使用仿射分段模型的自适应预测控制器,随着旋翼飞行器飞行状态的改变而选择相应的控制参数.希腊学者Alexis等[15]对旋翼模型进行降阶解耦处理,基于该模型设计了可以控制位置和姿态的单个整合形式控制器.与此不同,Chen等[16]提出一种结构为级联形式的MPC控制器,用于四旋翼飞行器的位置和姿态控制.与单控制器控制策略相比较,使用级联结构的最大优点在于可以很好地处理某些作为控制量输入的状态变量所受到的约束条件,因此能稳定地将飞行器状态平衡点保持在一定范围.
本文研究基于MPC实现的四旋翼飞行器六自由度控制策略,与其它文献不同,本文采用完整的四旋翼动力学模型,不仅考虑执行机构的动态特性,并且控制输入为传统的操纵杆量,使得所设计的控制律可以与物理平台直接对接.控制器设计上还参考了国外学者以低维度拉盖尔基函数表征高维度向量的方法,降低了在线运算量.同时为了改善控制效果,本文考虑了对外界风扰的抑制,并利用输出偏差变化率避免了超调问题.提高抗风扰性能的做法是利用模型信息构建线性扩张状态观测器,估计外部阵风干扰,以观测值实时补偿控制输出.输出偏差变化率添加到预测控制器的目标函数中,相当于也对偏差进行优化控制,改善了动态特性.最后在半物理仿真平台上验证控制器设计原理的正确性,仿真结果表明本文设计的预测控制器具有抗干扰能力强、运算量低、工程可行性高的特点.
1 四旋翼动力学模型 1.1 非线性数学模型四旋翼运动方程不赘述,参见文[17],但与其不同,本文在机体受力模型中加入了机身的气动阻力,认为其与飞行器空速的平方成正比,方向相反,则合外力机体坐标分量为
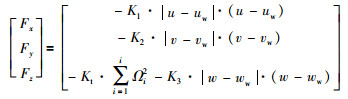
|
(1) |
式中,Ki(i=1,2,3)为气动阻力系数,u、v、w为线速度机体坐标分量,uw、vw、ww为风速,Kt为旋翼拉力系数,Ωi(i=1,2,3,4)为各旋翼转速.采用X型配置,合外力矩机体坐标分量为
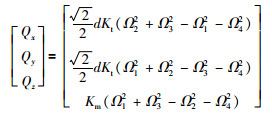
|
(2) |
式中,Km为旋翼反扭矩系数,d为机臂长度.
本文将飞行器的动力与执行机构即直流无刷电机描述为惯性环节:
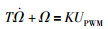
|
(3) |
式中,T为惯性时间常数,K为稳态增益,UPWM为输入PWM信号脉宽.
四旋翼的4个操纵杆量与传统直升机相同[δcol,δlon,δlat,δped],依次为总距、纵向周期变距、横向周期变距和尾桨距,通过分配映射及限幅得到4个电机的期望PWM信号脉宽值:
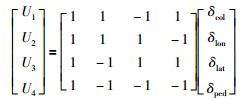
|
(4) |
四旋翼动力学系统具有强非线性,但通常工作在悬停点附近,可以线性化,采用线性MPC技术,降低实现难度,提高可行性.四旋翼飞行器的线性空间描述形式为
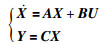
|
(5) |
式中控制量U、测量输出Y、状态量X依次为
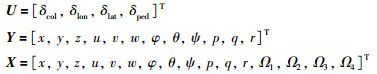
|
其中,x、y、z为导航坐标系中机体重心位置,φ、θ、ψ为机体姿态角,p、q、r为角速度机体坐标分量.特别注意以上各变量含义是相对于平衡点的偏差量,并且各旋翼转速不可测量.
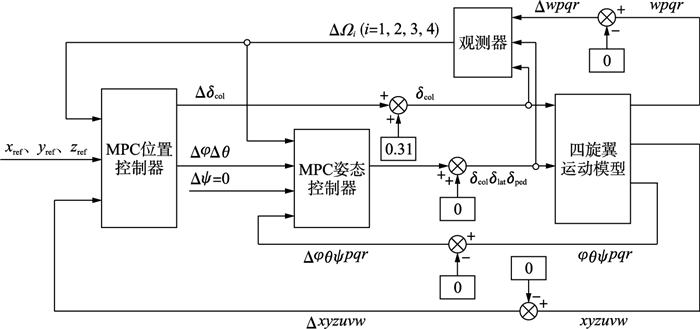
2 控制器设计四旋翼运动特性可分成姿态运动和质心运动,前者相较后者需要更快的响应速度,因此本文设计两个不同的控制器以级联结构对角运动和线运动分别进行控制,控制结构如图 1所示.外环是位置控制,给定输入为x、y、z三轴参考位置,输出是标准总距、期望滚转角和俯仰角的偏差量.内环完成姿态控制,输入是外环提供的期望滚转角和俯仰角偏差量及期望偏航角,输出为滚转、俯仰、偏航通道标准杆量偏差量.
|
| 图 1 级联MPC控制结构示意图 Figure 1 Cascaded MPC control structure diagram |
首先从式(5)抽取出内、外环被控对象状态空间模型,然后分别推导可用预测模型,进而完成内、外环控制器设计.其中,姿态运动线性化状态空间模型:
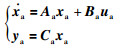
|
(6) |
式中,状态量、被控量、控制量依次为
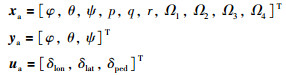
|
质心运动线性化状态空间模型:
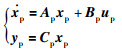
|
(7) |
式中,状态量、被控量、控制量依次为
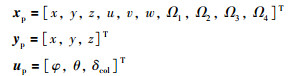
|
由于内外环设计方法和过程相同,下面仅以外环为例介绍.参考经典预测模型建立方法[18],首先按采样周期对上述模型离散化,然后定义状态增量与控制增量分别为
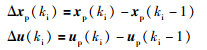
|
(8) |
再定义增广状态向量:
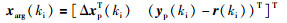
|
(9) |
其中r(ki)为参考量.建立以xarg(ki)为状态量、Δup(ki)为控制量、跟踪误差为输出量的增广模型:
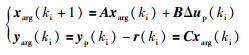
|
(10) |
式中,
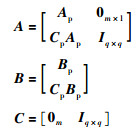
|
(11) |
由式(10)可建立经典形式预测模型:
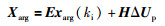
|
(12) |
式中,
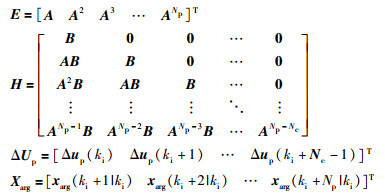
|
式中,Xarg为Np维预测状态向量,ΔUp为Nc维预测控制向量. Np和Nc为预测控制的重要参数,即预测时域长度和控制时域长度.其中Nc表示未来控制量改变的数目,其值越大,系统的控制能力越强,但同时也为待求序列ΔUp的维度.考虑到未来时刻约束条件,会带来运算量较大的问题,因此使用拉盖尔基函数[16],以低维向量表征控制量序列,减少运算量.
拉盖尔函数是一组维度为N的离散正交基函数,其Z变换形式为
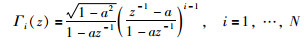
|
(13) |
定义 li(ki)为Гi(z)的逆z变换,a为可调比例因子,则拉盖尔函数离散形式满足差分方程:
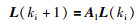
|
(14) |
式中,L(ki)=[l1(ki) l2(ki) … lN(ki)]T,矩阵Al和L(ki)初始值由比例因子a决定,形式为
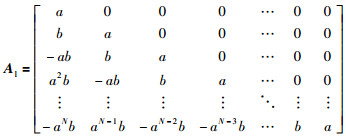
|
(15) |
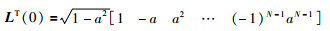
|
(16) |
式中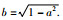
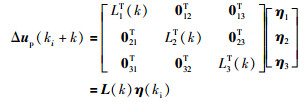
|
(17) |
式中,
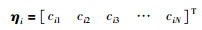
|
(18) |
注意 ηi(i=1,2,3)分别对应外环控制器的3个输出量,即标准总距偏差量、期望滚转角和俯仰角偏差量.将式(17)代入式(12)得到拉盖尔函数形式预测模型:
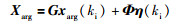
|
(19) |
式中,
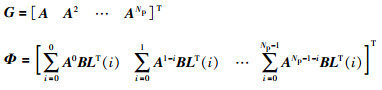
|
本文中有两处观测器设计,其一是旋翼转速的观测器,其二是干扰观测器.
为了观测旋翼转速偏差量,选取z轴速度、滚转、俯仰、偏航角速度偏差量为测量输出,构成4输入4输出系统:
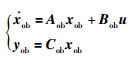
|
(20) |
式中状态量、测量输出和控制量依次为
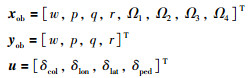
|
然后即可设计经典全维状态观测器,不赘述.
针对风扰观测,以纵轴方向为例,由悬停模型(5)可以抽取出带风扰的纵向运动模型:
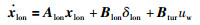
|
(21) |
式中状态量为
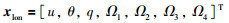
|
并且Bturuw=[D 0 0 … 0]T,D与风速成比例.定义增广状态向量xeso=[xlon D]T,并定义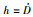
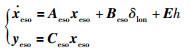
|
(22) |
式中
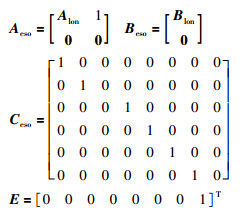
|
其中,Eh被认为是干扰项.对式(22)设计观测器,如果选择增益Lob使矩阵Aeso-LobCeso是赫尔维茨矩阵,则对此系统有界的干扰项h,观测器的估计误差是有界的[19].据此,对于有界外干扰D,观测器估计误差是有界的,只要合理调节观测器增益,可使其估计误差任意小.进而风速干扰值uw被反算出来,最终用于控制补偿.
2.3 控制量推导MPC控制器增益通过最小化目标函数计算得到.本文目标函数与文[16]所采用的经典形式相比,不仅引入了输出偏差变化率,改善系统的动态特性[20].还添加了风速干扰值来补偿控制量.其形式为
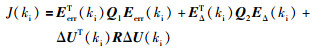
|
(23) |
式中,Q1=diag(q1i),Q2=diag(q2i),R=diag(ri),都为加权矩阵;向量Eerr的含义与经典形式相同,即未来预测时域内的输出偏差,EΔ则为该偏差的变化率,形式为
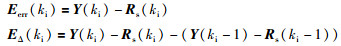
|
(24) |
式中的Y(ki)、Rs(ki)为预测时域内的预测输出和期望值向量.
为实现诸如来风时飞行器低头抵抗的效果,上节观测的风扰值需补偿内环控制输入,改变期望姿态角偏差量.于是,将观测的风扰uw、vw、ww代入式(9),定义外环位置控制器新的增广状态向量:
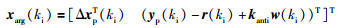
|
(25) |
式中,
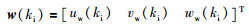
|
(26) |
kanti为比例系数,调节对内环输入的补偿程度.
将拉盖尔形式预测模型和式(17)用拉盖尔函数表征的控制增量序列代入目标函数可得:
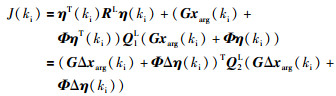
|
(27) |
式中Q1L=CTQ1C,Q2L=CTQ2C,Δxarg(ki)=xarg(ki)-xarg(ki-1). RL为对角矩阵,其阶数为所使用拉盖尔基函数维度N,对角线元素仍为权重值ri.可以将式(27)改写成:
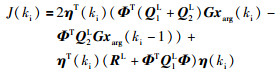
|
(28) |
由于采用悬停点线性化设计,外环输出的期望姿态角偏差量需有0.2 rad的幅值约束,因此外环控制未来第k时刻控制量的幅值应满足:
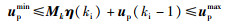
|
(29) |
式中,
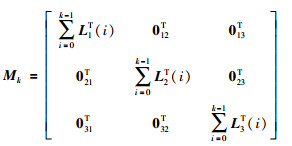
|
由式(29)可以写出线性不等式(30),M为约束边界.
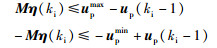
|
(30) |
式中,
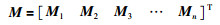
|
(31) |
M的列数n表示考虑未来第1个时刻到第n个时刻的约束条件.
式(27)和(29)的求解为标准二次型优化问题.本文使用简单的希尔德雷思算法解决该问题[13],得到最优解:
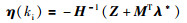
|
(32) |
式中,
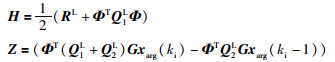
|
(33) |
λ*可由该算法的核心迭代公式求得. MPC策略具有滚动时域控制思想,只用每一时刻计算得到的最优控制序列的第1个分量,因此:
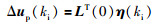
|
(34) |
最优控制偏差量为up(ki)=up(ki-1)+Δup(ki),该偏差加上配平值最终可得到最优输出量.
考虑式(30)的约束条件,控制律求解转化为非线性控制问题,可使用李亚普诺夫定理讨论闭环系统全局稳定性.
引理1[21] 假定每一时刻ki存在解向量η(ki),使目标函数满足式(29)的不等式约束和xarg(ki+Np|ki)=0的终端等式约束,则可保证系统稳定.
上述引理证明本文的控制设计是稳定的.另外,内环控制输出的计算过程与外环相同,只是具体模型不同,所用参数不同而已,不赘述.
3 半物理仿真验证本文设计了半物理仿真实验来验证控制效果,其中控制器采用自主开发的STM32F4芯片的飞控板实现,被控对象根据四旋翼飞行器非线性数学模型,采用台式机结合Qt 5. 2软件环境以C语言编程实现.
仿真中,外环控制器预测时域长度Np=150,加权矩阵权重值q1i=[0.05,0.05,0.1],q2i=[0.075,0.075,0],ri=[1.5,1.5,1.5],拉盖尔基函数参数a=0.9,N=3;内环控制器参数预测时域长度Np=60,权重值q1i=[0.2,0.2,0.2],q2i=[0, 0, 0],ri=[0.375,0.375,0.375],拉盖尔基函数参数a=0.65,N=3;kanti=0.017.横、纵轴的期望位置为5 m,z轴期望位置为-1 m.
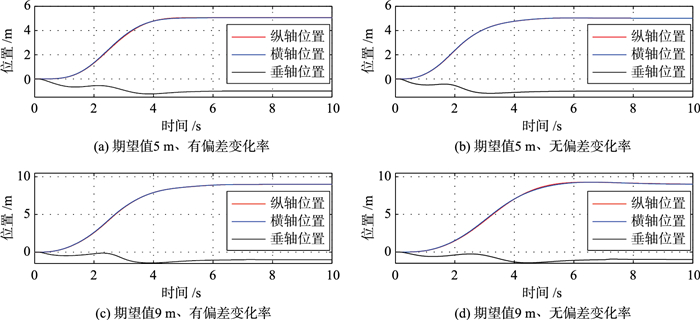
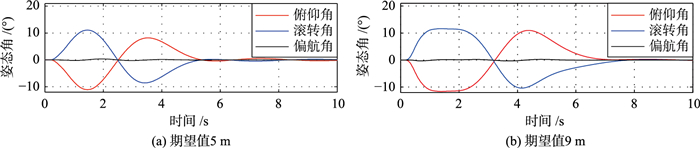
首先验证引入偏差变化率对控制性能的改进,分别设定期望位置为(5 m、5 m、-1 m)、(9 m、9 m、-1 m). 图 2(a)给出纵、横轴期望位置为5 m时,引入输出偏差变化率的控制效果,图 2(b)为不引入的情况. 图 2(c)、2(d)为期望位置为9 m时是否引入偏差变化率的两种控制效果. 图 3(a)、3(b)为两次位置控制的姿态角响应,并且是在不引入偏差变化率的情况下.
|
| 图 2 位置控制结果 Figure 2 Position control output |
|
| 图 3 姿态角响应结果 Figure 3 Attitude angle response result |
分析图 2、图 3的仿真结果.当期望位置从5 m增加到9 m,外环位置控制器的期望姿态角输出受到幅值约束的限制,没有超过0.2 rad,线性控制器增益变为非线性,如果目标函数不引入偏差变化率,位置输出响应出现超调的现象,并且可以预见随着期望位置的增大,超调的现象会更加严重.而通过在目标函数中引入偏差变化率则可以消除这种不利的现象,得到更好的位置控制效果.
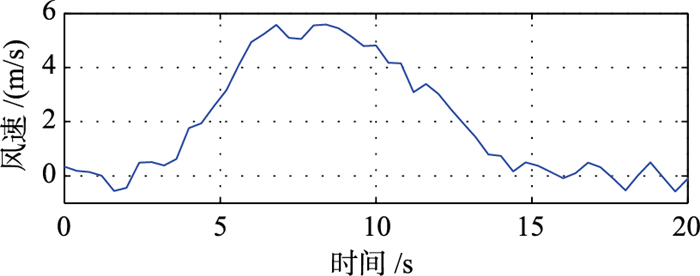
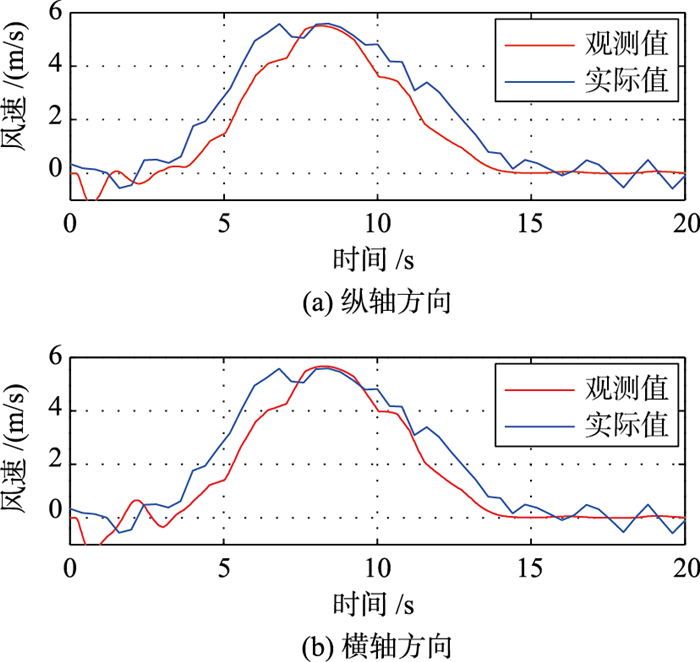
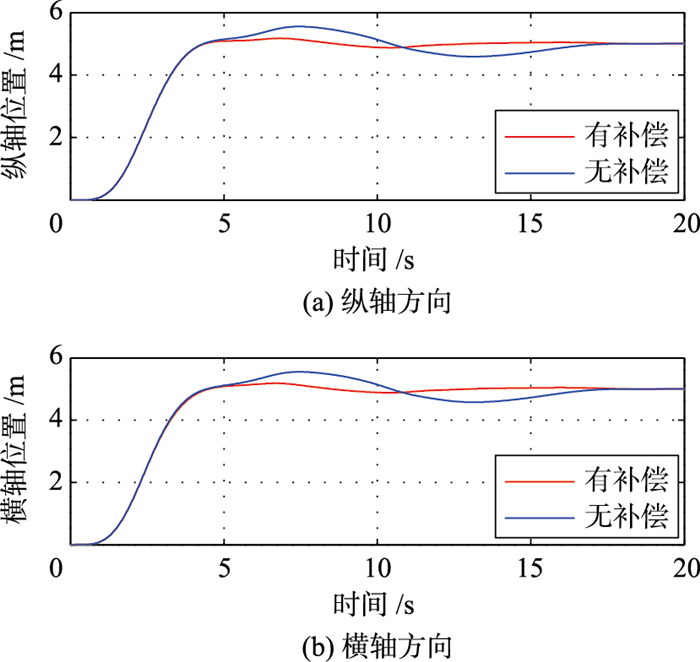
接下来验证系统的抗干扰性能,施加文[22]提供的阵风干扰信号,如图 4所示. 图 5(a)、图 5(b)显示了干扰观测器对横纵轴方向上扰动量的估计结果,可以看出由于模型准确性的问题,观测出的干扰风速值与实际值存在一定的误差,但能定性地跟踪干扰风的上升及下降趋势,有较好的观测效果,可以用于对期望姿态角输出的补偿. 图 6(a)表示在有、无干扰观测补偿的两种情况下,纵轴通道位置输出的响应结果. 图 6(b)表示横轴通道的结果.图中蓝色实线表示没有干扰补偿的情况,红色实线表示有补偿的情况.
|
| 图 4 风扰曲线 Figure 4 Wind disturbance curve |
|
| 图 5 风扰观测结果 Figure 5 Wind disturbance observation result |
|
| 图 6 纵、横轴位置输出结果 Figure 6 Longitudinal and horizontal position output |
如图 6所示,在无观测干扰补偿的情况下,MPC控制器仍能实现稳定控制,有一定的抵抗风扰能力,但干扰造成的输出波动幅值较大,为0.5 m左右,并且调节时间过长.而在有干扰补偿的情况下,输出波动幅值大大降低,位置输出能够在更短时间内回到期望值.因此可以认为使用干扰观测器的系统具有更强的抗干扰能力.
为了验证控制器的航迹跟踪效果,给定大机动的螺旋上升轨迹,参考位置为
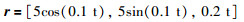
|
(35) |
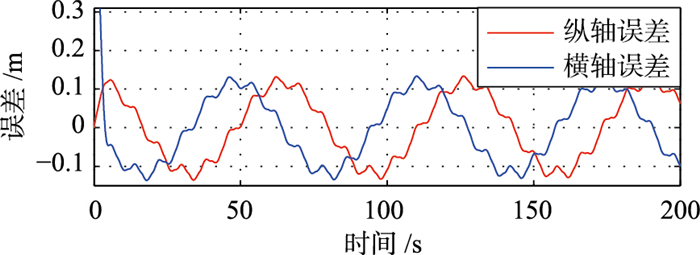
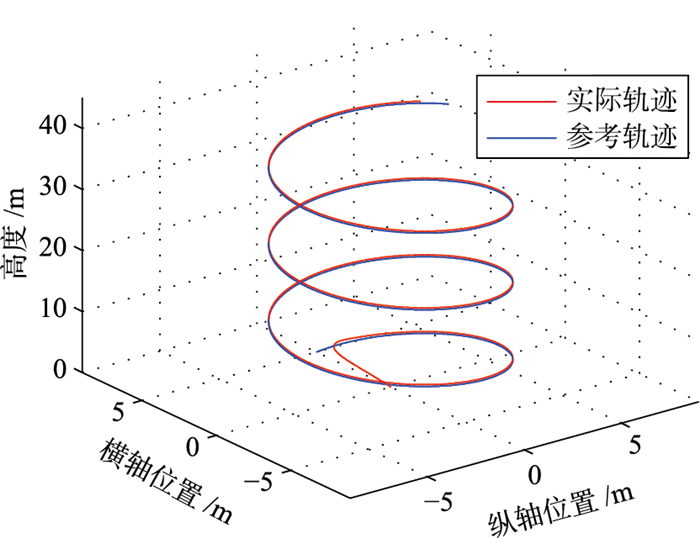
四旋翼飞行过程中受到方波形式的模拟阵风干扰,其波形设置为幅值等于2,周期为8 s,脉宽为4 s.仿真结果纵、横通道位置跟踪误差如图 7所示,蓝色实线是横轴方向跟踪误差,红色实线是纵轴方向跟踪误差.可见跟踪误差由相位延迟和风速干扰造成,误差收敛至0.15 m范围内,有较好的跟踪精度.最终三维飞行效果如图 8所示,蓝色实线是参考飞行轨迹,红色实线是实际飞行轨迹.可以看出,完成了对参考轨迹的跟踪,实现了螺旋上升大机动的飞行任务.
|
| 图 7 位置跟踪误差 Figure 7 Position tracking errors |
|
| 图 8 位置跟踪三维效果 Figure 8 Position tracking effect of 3D |
本文以四旋翼飞行器数学模型为基础建立控制器的预测模型和干扰观测器的扩张状态模型,设计了级联形式控制方案并实现对外界干扰的观测补偿,最后以半物理仿真对比实验验证了飞行控制效果,表明本文所设计的控制器具有较强的抗干扰性能,并且可以在嵌入式硬件平台上实现、运行,具有一定工程意义.
| [1] | Giitsidis T, Karakasis E G, Gasteratos A. Human and fire detection from high altitude UAV images[C]//23rd Euromicro International Conference on Parallel, Distributed and Network-Based Processing. Piscataway, NJ, USA: IEEE, 2015: 309-315. |
| [2] | Katsig P, Misopolinos L, Liakopoulos V, et al. An autonomous multi-sensor UAV system for reduced-input precision agriculture applications[C]//24th Mediterranean Conference on Control and Automation. Piscataway, NJ, USA: IEEE, 2016: 60-64. |
| [3] | Ramires J P, Doucette E A, Curtis J W, et al. Urban target search and tracking using a UAV and unattended ground sensors[C]//55th American Control Conference. New York, USA: ACM, 2015: 2401-2407. |
| [4] | Serra P, Cunha R, Hamel T, et al. Landing of a quadrotor on a moving target using dynamic image-based visual servo control[J]. IEEE Transactions on Robotics, 2016, 3(99): 1–12. |
| [5] | Bi Y C, Shan M, Li J X, et al. An autonomous quadrotor for indoor exploration with laser scanner and depth camera[C]//12th IEEE International Conference on Control and Automation. Piscataway, NJ, USA: IEEE, 2016: 50-55. |
| [6] | Arifudin M L, Hendro N. Preliminary study on unmanned aerial vehicle quadcopter using PID controller[C]//20th International Conference on Advanced Mechatronics, Intelligent Manufacture, and Industrial Automation. Piscataway, NJ, USA: IEEE, 2015: 34-37. |
| [7] | Sarthak K, Manish K, Kelly C. Genetically tuned LQR based path following for UAVs under wind disturbance[C]//14th International Conference on Unmanned Aircraft Systems. Piscataway, NJ, USA: IEEE, 2016: 267-274. |
| [8] |
曹美会, 鲜斌, 张旭, 等.
基于视觉的四旋翼无人机自主定位与控制系统[J]. 信息与控制, 2015, 44(2): 190–196.
Cao M H, Xian B, Zhang X, et al. An autonomous vision-based localization and control system for quadrotor UAV[J]. Information and Control, 2015, 44(2): 190–196. |
| [9] | Lu H, Liu C, Coombes M, et al. Online optimisation-based backstepping control design with application to quadrotor[J]. IET Control Theory and Applications, 2016, 10(14): 1601–1611. DOI:10.1049/iet-cta.2015.0976 |
| [10] | Reinoso M J, Minchala L I, Ortiz P, et al. Trajectory tracking of a quadrotor using sliding mode control[J]. IEEE Latin America Transactions, 2016, 14(5): 2157–2166. DOI:10.1109/TLA.2016.7530409 |
| [11] | Cisneros P S, Hoffmann C, Bartels M, et al. Linear parameter-varying controller design for a nonlinear quadrotor helicopter model for high speed trajectory tracking[C]//56th American Control Conference. New York, USA: ACM, 2016: 419-428. |
| [12] | Chen F Y, Wu Q B, Jiang B, et al. A reconfiguration scheme for quadrotor helicopter via simple adaptive control and quantum logic[J]. IEEE Transactions on Industrial Electronics, 2015, 62(7): 4328–4335. DOI:10.1109/TIE.2015.2389760 |
| [13] |
孙秀云, 方勇纯, 申辉.
无人直升机姿态通道模型预测控制[J]. 控制工程, 2014, 21(5): 643–647.
Sun X Y, Fang Y C, Shen H. Model predictive control for the attitude channel of unmanned helicopter[J]. Control Engineering of China, 2014, 21(5): 643–647. |
| [14] | Mujtaba J, Leo S, Jason F, et al. Experimental quadrotor flight performance using computationally efficient and recursively feasible linear model predictive control[J]. International Journal of Control, 2013, 86(12): 2189–2202. DOI:10.1080/00207179.2013.804256 |
| [15] | Alexis K, Nikolakopo G, Tzes A. Switching model predictive attitude control for a quadrotor helicopter subject to atmospheric disturbances[J]. Control Engineering Practice, 2011, 23(3): 1195–1207. |
| [16] | Chen X, Wang L P. Cascaded model predictive control of a quadrotor UAV[C]//3rd Australian Control Conference. Piscataway, NJ, USA: IEEE, 2013: 354-359. |
| [17] |
刘莉欣. 微小型四旋翼飞行器辨识建模研究[D]. 南京: 南京航空航天大学, 2014. Liu L X. Model identification of a miniature quadrotor helicopter[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014. |
| [18] |
钱积新, 赵均, 徐祖华.
预测控制[M]. 北京: 化学工业出版社, 2007: 72-73.
Qian J X, Zhao J, Xu Z H. Predictive control[M]. Beijing: Chemical Industry Press, 2007: 72-73. |
| [19] | Gao Z Q. Active disturbance rejection control: A paradigm shift in feedback control system design[C]//46th American Control Conference. New York, USA: ACM, 2006: 7-8. |
| [20] |
曾小勇, 彭辉, 吴军.
基于RBF-ARX模型的改进多变量预测控制及应用[J]. 中南大学学报:自然科学版, 2015, 25(10): 3710–3717.
Zeng X Y, Peng H, Wu J. An improved multivariable RBF-ARX model-based nonlinear model predictive control approach and application[J]. Journal of Central South University:Science and Technology, 2015, 25(10): 3710–3717. |
| [21] | Wang L P. Model predictive control system design and implementation using Matlab[M]. Berlin, Germany, 2009: 127-131. |
| [22] |
杜作义, 马乐瑶.
基于Matlab/simulink的风速仿真研究[J]. 中国西部科技, 2013, 12(24): 46–47.
Du Z Y, Ma L Y. Wind speed simulation based on Matlab/simulink[J]. Science and Technology of West China, 2013, 12(24): 46–47. |



