0 引言
目前,电子稳像技术已广泛应用在汽车监控系统和船载视频成像系统等应用领域中用于视频防抖处理,获得平滑稳定的视频图像序列[1-2].常见电子稳像算法包括SIFT法[3]、灰度投影法[4]、光流法[5]等多种根据图像特征信息进行电子稳像的方法.主要原理是估计当前帧相对于参考帧的全局运动,并进行运动补偿.然而仅利用图像信息获取全局运动容易受运动物体闯入或者图像特征、纹理信息不足等因素影响引起的图像信息匹配错误甚至无法匹配等问题.
针对以上问题,许多学者提出采用IMU或陀螺仪的方式实现相机运动的方法.张永祥[6]在船载电子稳像系统中将螺仪坐标系与相机坐标系人为对应进行安装,使得各个轴方向一致,然后直接利用陀螺仪数据对视频帧进行运动补偿,达到稳像目的.这种方法很难确保两个坐标系中各方向精确对应而导致稳像存在较大误差.王日俊[7]在载有相机和IMU的无人机导航系统中,通过IMU采集数据信息,反馈到CPU上,并通过PID(proportional-integral-derivative)方法[8]控制直流电机,使电机做出相应的反馈动作,保持无人机上装载的相机拍摄过程平稳.然而该方法无法实时精确转换相机到相应稳定的角度上,也给PID过程带来了很大压力.本文提出在稳像系统中对惯性测量单元和摄像机进行相对位姿标定并使用时间同步技术,使得IMU设备可安装在相机上的位置不受严格约束,降低了系统应用复杂度并有效抑制了由于装配原因导致的二者坐标轴不重合所引起的稳像误差.
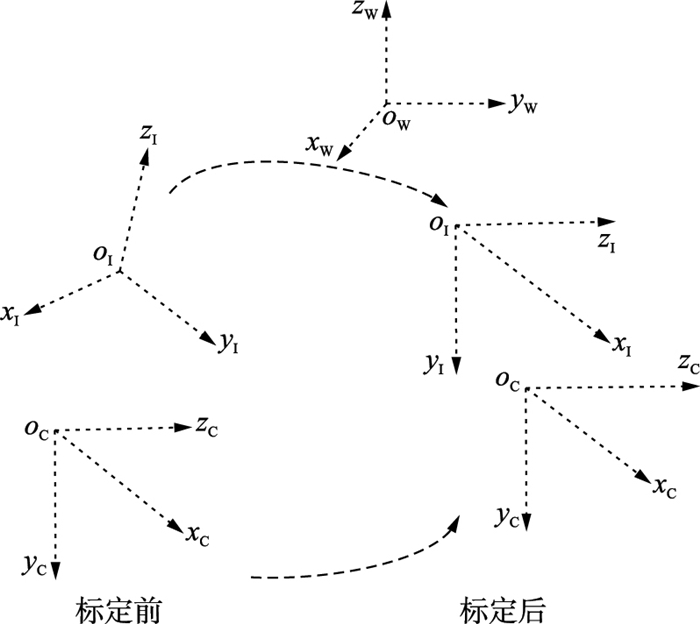
1 IMU-相机标定方法 1.1 IMU-相机相对位姿标定为了有效利用IMU提供的运动参数信息,需要将IMU和相机进行相对位姿标定.如图 1所示,左侧为标定前的IMU坐标系xIyIzI及相机坐标系xCyCzC,右侧为利用世界坐标系标定好的IMU坐标系和相机坐标系.
|
| 图 1 IMU与相机坐标系标定前后的关系 Figure 1 Relationship between the IMU and the Camera Coordinate systems before and after the calibration |
IMU和相机相对位姿标定首先利用刚性连接在一起的IMU和相机采集同一时刻数据信息,即相机采集棋盘格图像,IMU采集三轴加速度数据.连续采集n次后,利用对坐标系xCyCzC和xWyWzW进行棋盘格标定,对采集的图像求解相机坐标系与世界坐标系之间的旋转关系.将IMU和相机分别相互对应的点集,根据Horn[9]提出的基于四元数的最优旋转方法对IMU坐标系与相机坐标系进行相对位姿标定,求解相机与IMU之间的刚体变换关系[10],从而计算出相机坐标系和IMU坐标系的相对位姿关系.标定完成后,IMU位姿变化可正确反映到相机坐标系中.
使用张正友标定法[11]对n张连续拍摄的棋盘格图像序列确定相邻2张图像之间的旋转关系.对于世界坐标系中任意一点W,第i时刻和第j时刻对应的相机坐标系下的坐标分别为Xi、Xj,世界坐标系与相机坐标系之间存在旋转矩阵Ri、Rj和平移向量di、dj.它们之间的刚体变换关系如式(1)所示:
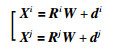
|
(1) |
把IMU通过导航坐标系对其自身姿态进行姿态运动学描述采集的三轴重力加速度矢量[12]及相机坐标系与世界坐标系的旋转关系中的重力运动矢量分别作为IMU坐标系和相机坐标系在同一个姿态下采集的数据点.设IMU三轴数据点表示为{Ii}.相机的数据点表示为{Ci}.相机坐标系和IMU坐标系各点对的坐标分别为Ci=[xC,i,yC,i,zC,i]、Ii=[xI,i,yI,i,zI,i];Np为匹配点对的个数,一般Np远大于3(计算刚体变换至少需3对匹配点).利用最小二乘法求解IMU坐标系和相机坐标系之间的旋转关系,如式(2)所示:
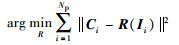
|
(2) |
其中,R(Ii)=[xI,ir yI,ir zI,ir]为IMU通过旋转矩阵R转换后的坐标点.将式(2)中的目标函数展开为
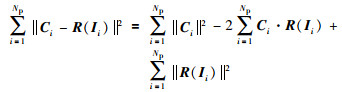
|
(3) |
由于两点对间仅为刚性变换,故‖R(Ii)‖2=‖Ci‖2.则上述展开式的最小化问题变为第2项的最大化问题:
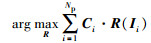
|
(4) |
已知IMU坐标系与相机坐标系之间的旋转矩阵R为正交阵.将Ii与R(Ii)的各轴坐标点转换到四元数空间,即ρI=[0 xI,i yI,i zI,i],ρR=[0 xI,ir xI,ir xI,ir].根据四元数的旋转变换性质[13]可以将Ii看作绕Γ轴旋转β角得到R(Ii).四元数q=[r0 r1 r2 r3]满足:
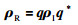
|
(5) |
对式(4)进行改写:
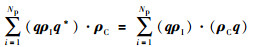
|
(6) |
其中,四元数q*=[r0 -r1 -r2 -r3]为q的共轭.设ρC=[0 xC,i yC,i zC,i]为相机坐标点的四元数表示,根据四元数乘法法则可知:
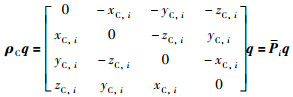
|
(7) |
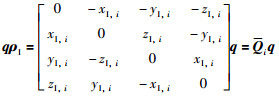
|
(8) |
Pi和Qi是反对称阵且正交,将式(7)和式(8)代入式(6)改写为
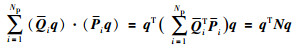
|
(9) |
其中,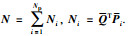
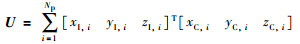
|
(10) |
U矩阵为相机点和IMU点的累积和,将U改写为矩阵形式:
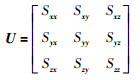
|
(11) |
其中,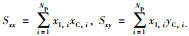
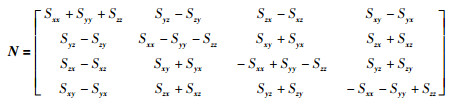
|
(12) |
使式(9)最大的四元数为矩阵N的最大特征值对应的特征向量,因此IMU与相机之间的四元数为qI_C=[q0 q1 q2 q3].再通过四元数与旋转矩阵之间的转换公式,求出IMU坐标系和相机坐标系之间的旋转关系R:
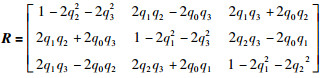
|
(13) |
将相机和IMU标定在同一坐标系下能更加准确地通过IMU的数据反映相机的运动信息.然而对于IMU和相机,它们的起始工作时间、采样频率可能均不相同.因此,对于IMU和相机同一时刻所采集的数据很难保持同步,需要频率同步和时间同步.
1.2.1 频率扩展本文通过牛顿插值法对IMU和相机的采样频率进行扩展.牛顿插值法的思想是以商差的基础上计算定义在每段单位区间上插值节点的变化率.
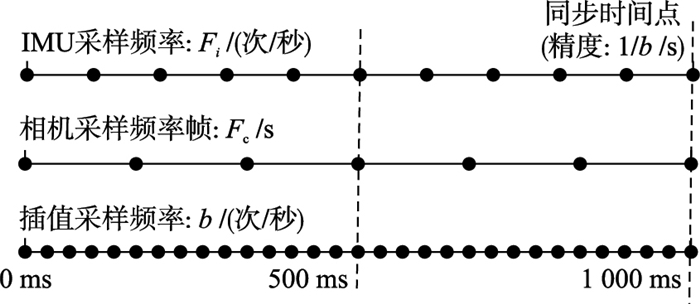
如图 2所示,设惯性传感器的频率为Fi,相机的频率为Fc,则两个传感器扩展后的频率应满足b=FiFc/d.其中,d为Fi和Fc的最大公约数,b为Fi和Fc的最小公倍数.
|
| 图 2 IMU与相机插值采样频率示意图 Figure 2 Schematic diagram of the interpolation sampling between the IMU and the camera |
设扩展后IMU的插值采样频率范围为xi={xi1,xi2,xi3,…,xin},相机的插值采样频率范围为xc={xc1,xc2,xc3,…,xcn}.集合xi与集合xc的元素个数相同且相邻元素间隔大小相同.
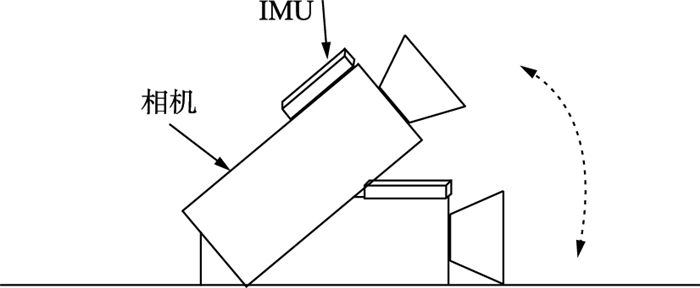
1.2.2 时间同步本文将标定在同一坐标系下的IMU与相机放置在一个静止的平台上;启动IMU和相机进行捕捉在静止状态下的图像信息及IMU姿态信息;再以相机底部为轴,使镜头向上做往复运动.得到IMU和相机各个坐标轴从静止到运动的轨迹.如图 3的本文前期工作[14]所示,利用运动模型对IMU和相机进行相同采样频率下的时间触发同步.
|
| 图 3 特定运动模型 Figure 3 The specific motion model |
设在整个时间轴上IMU与相机从静止到运动的时间点分别为ati与atc.以IMU时间点ati为匹配模板,截取一小段以ati为中心点的匹配模板时间段,记为[ati-δ,ati+δ],其中δ > 0为模板匹配段的阈值.在相机模板匹配段取[atc-θ,atc+θ]作为与其匹配的匹配段,其中θ > δ.
再根据最小二乘法的思想[15]将模板按顺序与匹配段的数据进行匹配计算求得误差平方和最小的时间段所对应的时间.公式表示为
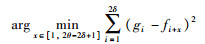
|
(14) |
其中,gi为模板匹配段的数据集合,fi+x为匹配段的数据集合.进而求解两个传感器之间的时间误差.利用特定运动模型来解决IMU与相机之间的时间同步问题.
2 视频稳像算法在IMU坐标系与相机坐标系相对位姿标定和数据触发时间同步的基础上,利用IMU对相机进行运动估计,把IMU数据的弧度信息作为旋转向量求解旋转矩阵,再根据在不同平面上的同一特征点对应世界坐标系上同一点的性质,计算连续帧间的单应性,实现帧间稳像.
2.1 连续帧间单应性估计 2.1.1 计算旋转矩阵由1.1节可知,将IMU坐标系转换到相机坐标系的旋转关系为R.假设通过IMU可知第i帧在XYZ轴形成的旋转矩阵为RI,那么利用IMU表示相机在第i帧的姿态,如式(15)所示:
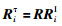
|
(15) |
将Rτ转换成各轴的旋转角分别为xa、ya和za,记作向量v =[xa ya za]T.把旋转角作为旋转向量求解单位化旋转矩阵,对向量v进行规范化得到:
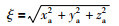
|
(16) |
其中ξ为规范化长度.再将向量v中各个值除以ξ,得到模长为1的单位化旋转向量e =[e1 e2 e3]T:
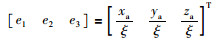
|
(17) |
将单位化旋转向量改写成斜对称矩阵:
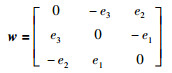
|
(18) |
将式(16)、式(18)代入式(19),根据罗德里格斯[16]绕任意轴旋转的几何关系公式得到传感器第i帧所形成的单位化旋转矩阵Ei为
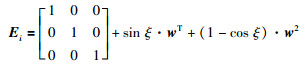
|
(19) |
设x为第1幅图像的特征点集,x'为第2幅图像中对应的特征点集,则有对应关系:x'= Hx.进而通过单应性[17]矩阵H计算两帧之间的映射关系.
设相机的内参矩阵为K,由式(19)可知第i帧所形成的单位化旋转矩阵为Ei.根据两个平面上同一个点对应同一个世界坐标系上的点可以推出,单应矩阵H=KEiK-1.
2.2 连续帧抖动抑制通过2.1节计算得出两个连续帧之间的单应性矩阵H,对第i帧进行稳像.设第i帧稳像前图像中点的坐标为[pi,qi]T,稳像后为[pi',qi'],则它们之间的关系[18]满足:
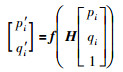
|
(20) |
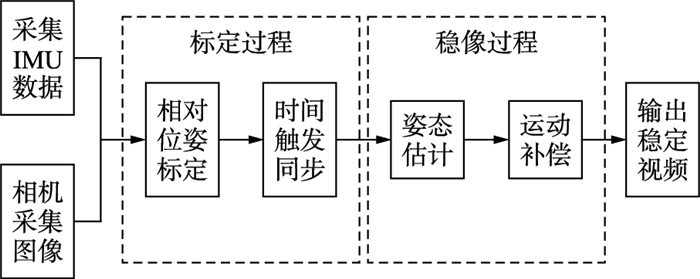
其中,f([xi,yi,zi]T)=[xi/zi,yi/zi]T为3维欧氏空间到2维欧氏空间的一个映射,[xi,yi,zi]T=H[pi,qi,1]T.进而通过上述方法完成了利用IMU姿态信息,进行电子稳像的目的,其总体流程图如图 4所示.
|
| 图 4 总体流程图 Figure 4 The overall flow chart |
本实验平台如图 5所示,将IMU贴合在相机上形成刚体连接,二者之间相对姿态任意.相机为Allied Vision Technologies公司的GX1910工业相机,使用1 920×1 080分辨率,采样频率为25 f/s. IMU使用MPU6050(含3轴加速度计和陀螺仪),波特率设置为115 200,帧频100 Hz.磁传感器为HM5883L电子罗盘,实现对MPU6050的Z轴航向角进行校正.计算机主频为1.4 G双核心,内存4 G.

|
| 图 5 实验平台 Figure 5 The experimental platform |
陀螺仪存在自身的温差漂移[19],若单一的使用陀螺仪积分求取系统姿态则会存在误差累积的问题.由于加速度计的低频特性好而陀螺仪的高频特性好,可采用互补滤波的方法对加速度计数据的进行融合.故此绕X轴和Y轴旋转的角速度都可以得到加速度计在它们各轴上的分量,并得以校正.由于绕Z轴旋转的陀螺仪角速度所得到的加速度分量始终为0,因此不能利用加速度对陀螺仪的Z轴角速度进行互补校正.本文使用磁传感器对Z轴漂移进行矫正得到旋转角度,其原理是地磁场对于固定的点的航向角等于该点当前方向和磁北方向的夹角,由于地磁场相对比稳定,故此使用磁传感器来校准陀螺仪的航向角.
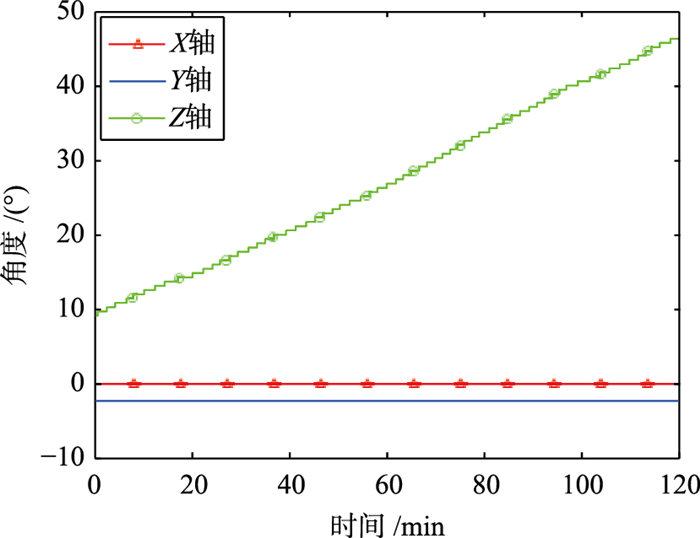
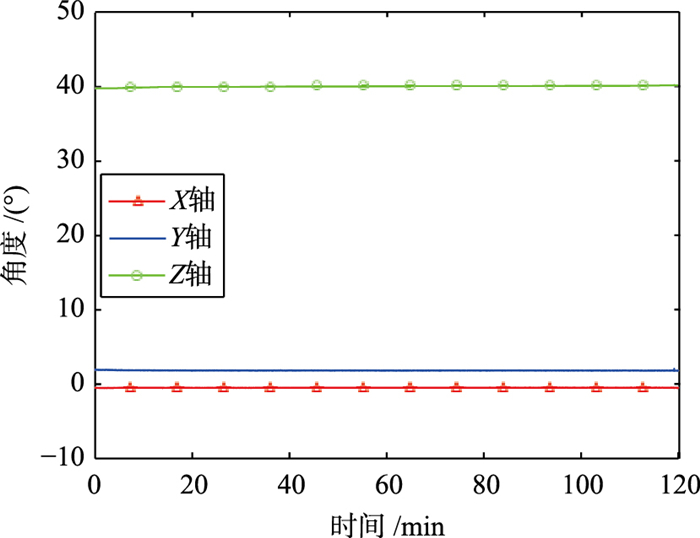
图 6为不使用磁传感器将IMU静止放置2小时测得的IMU各轴累计误差曲线. 图 7为利用磁传感器对IMU的Z轴航向角进行校正测得的IMU各轴累计误差曲线.实验结果表明,使用磁传感器对IMU的Z轴航向角进行校准,可有效解决由于陀螺仪自身漂移导致的累计误差问题.
|
| 图 6 校准前IMU各轴累计误差曲线 Figure 6 IMU cumulative error curve before the calibration |
|
| 图 7 校准后IMU各轴累计误差曲线 Figure 7 IMU cumulative error curve after the calibration |
对IMU坐标系和相机坐标系进行标定,首先要对相机进行棋盘格标定,在空间中放一张12×12的标定板,每个棋盘格的边长为37 mm.使整个标定板在相机的视场范围内,固定标定板的位置,然后运动相机采集图像.当相机在某一个位置采集标定板图像的同时采集IMU数据. IMU得到以重力方向为基向量的三轴加速度矢量作为IMU的数据点;相机得到以相机坐标系重力方向为基向量的3轴加速度矢量,作为相机的数据点.
| 序号 | X轴 | Y轴 | Z轴 |
| 1 | 0.050 3 | -0.043 0 | 1.006 8 |
| 2 | -0.017 6 | -0.189 0 | 0.993 2 |
| 3 | -0.074 2 | -0.334 0 | 0.938 0 |
| 4 | 0.141 6 | 0.251 0 | 0.964 8 |
| 5 | 0.286 6 | 0.377 0 | 0.895 0 |
| 6 | 0.193 8 | -0.078 6 | 0.985 4 |
| 7 | 0.365 2 | 0.543 5 | 0.769 5 |
| 8 | -0.059 1 | -0.437 0 | 0.896 0 |
| 序号 | X轴 | Y轴 | Z轴 |
| 1 | 0.028 1 | -0.996 3 | 0.081 8 |
| 2 | 0.182 0 | -0.979 0 | 0.091 9 |
| 3 | 0.330 1 | -0.938 3 | 0.103 6 |
| 4 | -0.281 8 | -0.958 8 | 0.036 7 |
| 5 | -0.454 9 | -0.884 6 | 0.102 8 |
| 6 | -0.015 1 | -0.973 3 | 0.229 2 |
| 7 | -0.636 5 | -0.764 9 | 0.098 6 |
| 8 | 0.418 8 | -0.894 0 | 0.159 4 |
将采集到的8组IMU和相机数据使用1.1节中的四元数法进行标定,求解两个坐标系之间的相对位姿. IMU坐标系旋转到相机坐标系的求解结果是[177.865 4,-63.325 8,-87.307 8].将求解出的角度转换为旋转矩阵R为
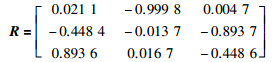
|
(21) |
为了验证旋转矩阵的准确性,分别把IMU和相机采集的数据点作为点云且一一对应.利用3×3的旋转矩阵乘以3×n(n代表采集了n次)的IMU点云,得到变换后的IMU点云.若变换后的IMU点云与相机点云匹配,则旋转矩阵求解正确.
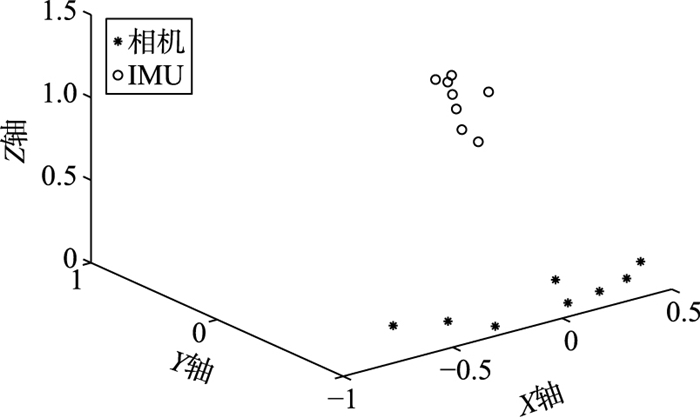
图 8为标定前IMU和相机数据点的位置关系,其中,"o"表示标定前IMU在各个姿态下采集的数据点坐标,"*"为相机在各个姿态下采集相机的数据点坐标.观察可知,标定前IMU和相机坐标点不重合.
|
| 图 8 标定前点云关系 Figure 8 The points' cloud relationship before the calibration |
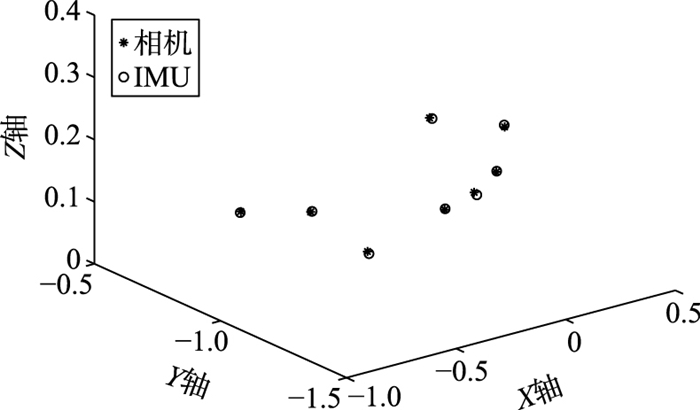
图 9为利用求解出的旋转矩阵,对IMU数据点进行旋转后,与相机数据点重合的点云关系.
|
| 图 9 标定后的点云关系 Figure 9 The Points' cloud relationship after the calibration |
计算相对位姿标定前后点云之间的欧氏距离,设相机坐标为[xc,yc,zc],IMU坐标为[xI,yI,zI],则:
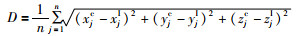
|
(22) |
其中,D为点云之间的欧氏距离,n为采集数据点的总个数.针对本次实验中任意摆放的IMU和相机进行相对位姿标定.标定前点云之间的欧氏距离为0.488 9,标定之后点云之前的欧氏距离为0.003 5.标定后的两个点云基本重合,验证了标定的准确性.
3.3 时间同步实验将标定好的IMU和相机进行频率配准.已知IMU频率为100 Hz,相机的频率为25 Hz,通过1.2节描述的方法,将IMU和相机的频率通过插值各自扩展到100 Hz.
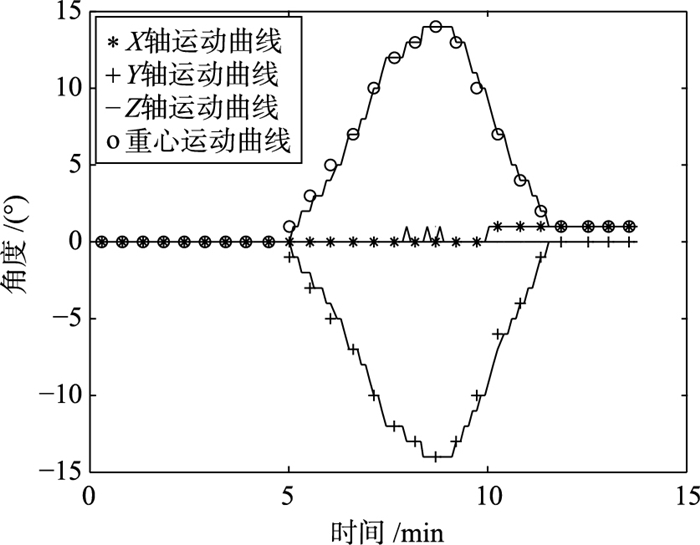
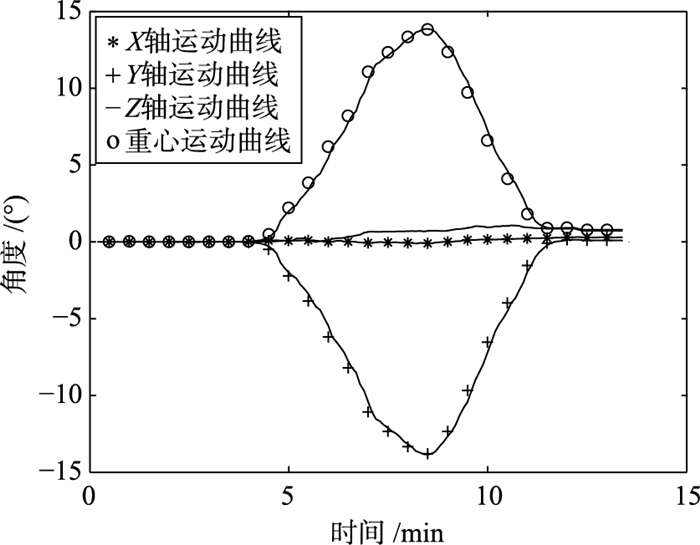
图 10和图 11分别为相机和IMU的运动轨迹,其中,"*"分别为IMU和相机X轴运动曲线,"+"为Y轴运动曲线,"-"为Z轴运动曲线,"o"为重心运动曲线.观察可知,4条曲线在起始位置各个轴并未发生角度变化,经过一段时间后IMU和相机各轴角度发生变化,此时运动曲线由直线变为曲线.
|
| 图 10 相机运动轨迹 Figure 10 The camera motion trajectory |
|
| 图 11 IMU运动轨迹 Figure 11 The IMU motion trajectory |
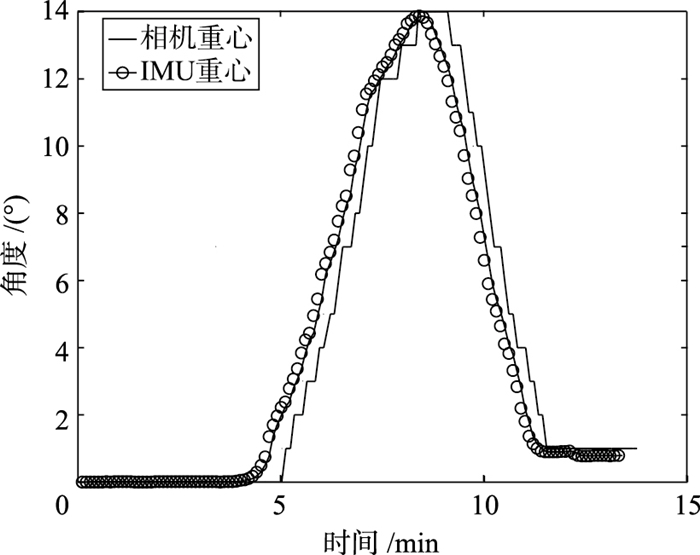
将刚性连接的IMU和相机先静止的放置一段时间后同时运动,进而得到IMU和相机各个轴运动过程中角度变化的信息.分别将IMU和相机各自轴角度平方求和,再开方计算得到IMU和相机的重心运动曲线.使用重心运动曲线进行时间同步避免了只利用单坐标轴进行时间同步过程中,因该坐标轴运动趋势过小而导致无法进行最小误差匹配的弊端.因此,分别提取图 10、图 11中的重心曲线和运动曲线进行时间同步,如图 12所示.
|
| 图 12 比较IMU和相机重心的运动轨迹 Figure 12 Comparison of the motion trajectory between the IMU and the camera |
把相机重心运动曲线与IMU重心运动曲线进行最小误差段匹配,其最小误差值为0.575 3.如图 12所示,相机从静止到运动的触发时间为5 s;IMU从静止到运动的触发时间为4 s.通过计算相机和IMU的触发时间差可知,IMU在某一时刻的位姿数据对应相机从这一时刻开始1 s后的视频帧.
3.4 稳像效果及比较实验本节对4种常见场景包括室内纹理充足场景,室内纹理不足场景,室外纹理充足场景及室外纹理不足场景.对相机采用的抖动方式均为手持上下或左右40°范围内无规则晃动,进而验证本文所提算法的有效性.并对室内两种不同情况的场景进行连续多帧的稳像评价,对室外两种场景进行单帧稳像评价,观察使用IMU稳像的实验结果.
3.4.1 评价方法本文利用均方差(mean squared error,MSE)算法和峰值信噪比(peak signal to noise ratio,PSNR)及帧间相似度评价方法对IMU方法和SIFT方法、灰度投影法的稳像效果进行对比分析[20].
均方差法是计算两帧图像相对灰度值的偏差大小:
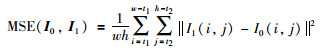
|
(23) |
其中,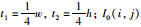
峰值信噪比是比较参考帧与当前帧灰度值差异,PSNR值越大稳像效果越好.
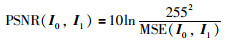
|
(24) |
帧间相似度指计算参考帧和当前帧图像的重合情况,如式(24)所示:
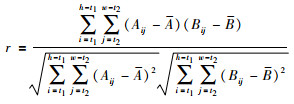
|
(25) |
其中,r为参考帧与稳像帧之间相似度,取值范围[-1, 1],相似度越接近1稳像效果越好;h和w为图像的高和宽;Aij和Bij分别为参考帧与稳像帧图像中的(i,j)位置的像素值;A和B分别为参考帧与稳像帧所有像素值的均值.
3.4.2 室内纹理充足场景实验场景1为室内纹理信息充足场景. 图 13(a)、图 13(b)为参考帧和当前帧,图 13(c)、图 13(d)和图 13(e)为采用不同方法进行稳像的效果.为方便观察稳像效果,图中用黑色十字线对展示板的边缘做了标记.实验结果表明SIFT及本文方法在特征较多的情况下,稳像结果相似,均得到了较好的稳像效果.由于该场景中存在旋转运动,因此灰度投影法表现出了较大误差.

|
| 图 13 场景1室内纹理充足场景 Figure 13 The indoor scene 1 with the sufficient texture |
以实验场景1为例,使用本文方法求得图 13(a)、图 13(b)中参考帧与当前帧之间的单应性矩阵为HI,通过该单应性矩阵进行稳像可得到图 13(c)的实验效果:
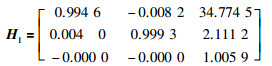
|
(26) |
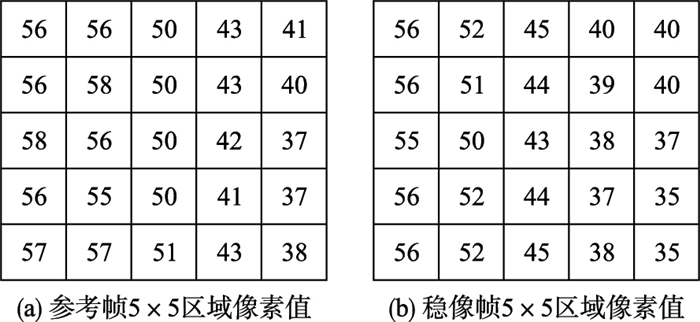
并对图 13(a)参考帧和图 13(c)稳像后的图像进行相似度比较,把图中用黑色十字线作为中心,选取5×5的区域进行相似度比较,图中方形黑色虚线框为扩大后该区域所在位置标识. 图 14(a)为参考帧5×5区域的像素值,其整体像素均值A为48. 84. 图 14(b)为稳像帧5×5区域的像素值,该区域的整体像素均值B为45. 44.将其代入式(25),得到图 13(a)、图 13(c)中参考帧与稳像帧5×5区域的相似度值为0.950 1.
|
| 图 14 参考帧与稳像帧5×5区域像素值分布列表 Figure 14 The reference frame and the stable frame pixel values distribution list in the 5×5 region |
表 3总结了不同算法的具体稳像评价结果.无特殊说明情况下,本文在稳像评价过程中,选取除去图像由于运动补偿产生的无效黑边区域,进行稳像评价.不失一般性,此处的MSE、PSNR及r分别为指定连续10帧对应统计量的平均值.此处,IMU稳像结果与SIFT相比统计结果相似,MSE值均较小;使用灰度投影算法MSE值较大,稳像效果不佳.对图像连续帧间的相似度进行百分比评价,IMU与SIFT帧间相似度百分比接近,较灰度投影算法提高约25%.
| 实验场景1 | 稳像方法 | MSE | PSNR | r |
| 第30帧~第40帧 | 本文方法 | 38.955 1 | 55.597 6 | 0.982 5 |
| SIFT | 31.846 7 | 63.245 4 | 0.985 8 | |
| 灰度投影 | 548.714 0 | 33.873 2 | 0.736 4 | |
| 第70帧~第80帧 | 本文方法 | 30.701 1 | 65.192 4 | 0.986 4 |
| SIFT | 37.284 5 | 58.790 7 | 0.986 1 | |
| 灰度投影 | 645.845 3 | 31.011 9 | 0.688 0 | |
| 第120帧~第130帧 | 本文方法 | 41.650 2 | 58.659 9 | 0.981 2 |
| SIFT | 40.699 8 | 56.723 2 | 0.982 4 | |
| 灰度投影 | 531.799 8 | 32.895 4 | 0.744 2 |
实验场景2为室内纹理不足场景.场景中,对特征点较少,特征信息相似的墙面进行电子稳像实验. 图 15(a)和图 15(b)为参考帧和当前帧,图 15(c)、图 15(d)和图 15(e)分别对应不同算法的稳像效果.对于特征点较少情况,本文方法能够更好的进行稳像,而SIFT方法存在误差和变形,箭头向右偏且箭头上下长度被压缩严重.灰度投影算法未得到理想的矫正效果.

|
| 图 15 场景2室内纹理不足场景 Figure 15 The indoor scene 2 with the insufficient texture |
表 4为对应实验统计数据.由于该场景为特征相似的墙面,并且标志物相对于图像较小,为了突出信号在噪声中的比例,该场景实验中在标识符周围选取60×60的区域进行稳像效果评价. SIFT及灰度投影算法与本文算法相比由于稳像过程中较多的依赖图像特征信息,稳像效果不明显.然而,IMU不依赖于图像特征的限制,因此稳像效果突出.视频连续帧间的相似度百分比评价本文方法,相对于SIFT提高了约20%.相对于灰度投影算法提高约40%.
| 实验场景2 | 稳像方法 | MSE | PSNR | r |
| 第30帧~第40帧 | 本文方法 | 45.033 4 | 68.891 9 | 0.947 8 |
| SIFT | 180.136 5 | 50.136 5 | 0.769 7 | |
| 灰度投影 | 368.430 7 | 37.379 0 | 0.525 0 | |
| 第70帧~第80帧 | 本文方法 | 54.270 6 | 65.758 7 | 0.934 7 |
| SIFT | 250.793 3 | 43.181 2 | 0.679 7 | |
| 灰度投影 | 377.166 1 | 41.539 8 | 0.536 2 | |
| 第120帧~第130帧 | 本文方法 | 59.386 3 | 68.037 6 | 0.926 1 |
| SIFT | 208.356 0 | 40.188 7 | 0.735 5 | |
| 灰度投影 | 494.338 6 | 34.788 5 | 0.361 4 |
实验场景3为室外纹理不足场景,对特征信息相似的天空进行稳像实验. 图 16为相机对着天空采集的视频图像,并在图中标记了一朵云作为稳像前的参照物和其在使用不同方法稳像后所在的位置.其中图 16(a)、图 16(b)为参考帧与当前帧. 图 16(c)、图 16(d)和图 16(e)分别为采用不同方法稳像的效果,通过云的位置变化观察得出SIFT稳像算法和灰度投影稳像算法对特征信息相似的天空未获得明显的稳像效果,本文提出的算法表现出较高的优越性.

|
| 图 16 场景3室外纹理不足场景 Figure 16 The outdoor scene 3 with theinsufficient texture |
表 5为统计分析结果.本文稳像方法中MSE的值远低于SIFT和灰度投影算法,PSNR值高于其它2个算法,说明本文稳像算法对室外纹理不足场景有较好的稳像效果,可以避免由于图像特征信息缺失导致的无法稳像的缺点.由于本次实验的场景信息相似,对不同算法进行帧间相似度比较结果接近.
| 实验场景3 | 稳像方法 | MSE | PSNR | r |
| 第21帧 | 本文方法 | 10.776 4 | 87.051 6 | 0.982 8 |
| SIFT | 133.910 4 | 61.853 6 | 0.854 5 | |
| 灰度投影 | 174.802 4 | 59.188 7 | 0.829 4 | |
| 第22帧 | 本文方法 | 13.549 9 | 84.761 5 | 0.979 3 |
| SIFT | 240.639 3 | 55.992 3 | 0.746 0 | |
| 灰度投影 | 244.805 8 | 55.820 6 | 0.743 1 | |
| 第23帧 | 本文方法 | 15.441 5 | 82.461 5 | 0.975 4 |
| SIFT | 87.414 8 | 66.118 6 | 0.895 8 | |
| 灰度投影 | 39.121 8 | 74.158 5 | 0.943 2 |
如图 17所示,对实验场景4室外纹理复杂场景中摆动的树木进行稳像.实验表明,尽管可选取纹理信息充足,但由于树木存在摆动等不利因素存在,导致基于纹理或特征点的算法出现较大误差.本文算法明显优于其它两种.

|
| 图 17 场景4室外纹理复杂场景 Figure 17 The outdoor scene 4 with thecomplex texture |
表 6为评价结果统计数据.由于背景中树是晃动的且受光照变化的影响,尽管各个算法对比稳像前后两幅图像,相似度均较低,但本文算法仍表现出较突出的评价值.该算法可以更有效地克服图像结构不稳定、纹理不足等不良信息对稳像算法的限制,表现出了高的鲁棒性.
| 实验场景4 | 稳像方法 | MSE | PSNR | r |
| 第51帧 | 本文方法 | 4 805.2 | 26.050 7 | 0.289 9 |
| SIFT | 5 315.2 | 25.041 9 | 0.249 4 | |
| 灰度投影 | 5 431.1 | 24.826 2 | 0.225 1 | |
| 第52帧 | 本文方法 | 5 099.2 | 25.456 9 | 0.262 2 |
| SIFT | 5 552.6 | 24.605 1 | 0.219 1 | |
| 灰度投影 | 5 617.6 | 24.488 7 | 0.210 4 | |
| 第53帧 | 本文方法 | 5 264.8 | 25.137 4 | 0.238 0 |
| SIFT | 5 806.3 | 24.158 2 | 0.193 5 | |
| 灰度投影 | 5 889.8 | 24.015 5 | 0.187 7 |
本文提出了一种在相机上搭载IMU的电子稳像方法.该方法通过将IMU和相机进行标定,将IMU的姿态数据实时反馈到相机上,进而达到视频帧稳定的效果.通过在多种场景下对比不同算法,本文提出的方法在特征点较多、并且特征较为稳定的场景中稳像效果和SIFT及灰度投影法相似.然而,在特征点信息较少、特征相似或特征点受外界因素影响而不稳定的场景中,由于搭载的IMU数据采集不受图像信息影响,稳像效果明显高于其它两种,具有最优的有效性和鲁棒性.本文算法与传统基于陀螺仪的方法,不仅能解决旋转等抖动,并且采用了磁传感器方法有效的抑制了漂移的问题.在军事、民用等领域均有广泛的应用价值.
| [1] |
李计添, 何永强, 陈财森, 等.
一种基于灰度投影算法的车载电子稳像方法[J]. 红外技术, 2010, 32(6): 328–332.
Li J T, He Y Q, Chen C S, et al. A method of vehicle-bone electronic image stabilization based on gray projection algorithm[J]. Infrared Technology, 2010, 32(6): 328–332. |
| [2] | Vella F, Castorina A, Mancuso M, et al. Digital image stabilization by adaptive block motion vectors filtering[J]. IEEE Transactions on Consumer Electronics, 2002, 48(3): 796–801. DOI:10.1109/TCE.2002.1037077 |
| [3] | Zhang Y, Yao H, Xu P, et al. Video stabilization based on saliency driven SIFT matching and discriminative RANSAC[C]//the Third International Conference on Internet Multimedia Computing and Service. New York, NJ, USA: ACM, 2011: 65-69. |
| [4] | Cheng L, Wang X P, Meng L Y, et al. Electronic image stabilization for railway crossing video based on gray projection[J]. Computer Engineering & Design, 2009, 30(2): 443–445. |
| [5] | Cai J H, Walker R. Robust video stabilisation algorithm using feature point selection and delta optical flow[J]. IET Computer Vision, 2009, 3(4): 176–188. DOI:10.1049/iet-cvi.2009.0036 |
| [6] |
张永祥. 基于陀螺仪的船载电子稳像技术研究[D]. 长春: 长春光学精密机械与物理研究所, 2006. Zhang Y X. Study on electronic image stabilization technology for the image sequences of the ship-borne camera system base on the gyro[D]. Changchun: Changchun Institute of Optic, Fine Mechanics and Physics, Chinese Academy of Sciences, 2006. |
| [7] |
王日俊. 多旋翼无人飞行器载荷稳像技术研究[D]. 长春: 长春光学精密机械与物理研究所, 2015. Wang R J, Study on image stabilization technology for the payload of mUAV[D]. Changchun: Changchun Institute of Optic, Fine Mechanics and Physics, Chinese Academy of Sciences, 2015. |
| [8] |
马增辉, 刘长良.
一类非最小相位系统的PID控制器整定方法[J]. 信息与控制, 2015, 44(2): 147–151.
Ma Z H, Liu C L. Tuning method for a PID controller in a non-minimum phase system[J]. Information and Control, 2015, 44(2): 147–151. |
| [9] | Horn B K P, Hilden H M, Negahdaripour S. Closed-form solution of absolute orientation using orthonormal matrices[J]. Journal of the Optical Society of America A, 1988, 5(7): 1127–1135. DOI:10.1364/JOSAA.5.001127 |
| [10] |
邱茂林, 马颂德, 李毅.
计算机视觉中摄像机定标综述[J]. 自动化学报, 2000, 26(1): 43–55.
Qiu M L, Ma S D, Li Y. Overview of camera calibration for computer vision[J]. Acta Automatica Sinica, 2000, 26(1): 43–55. |
| [11] | Zhang Z. A flexible new technique for camera calibration[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2000, 22(11): 1330–1334. |
| [12] |
吴哲明, 孙振国, 张文增, 等.
基于惯性测量单元旋转的陀螺漂移估计和补偿方法[J]. 清华大学学报:自然科学版, 2014, 54(9): 1143–1147.
Wu Z M, Sun Z G, Zhang W Z, et al. Gyroscope bias estimation and compensation by rotation of the inertial measurement unit[J]. Journal of Tsinghua University:Science and Technology, 2014, 54(9): 1143–1147. |
| [13] | Horn B K. Closed-form solution of absolute orientation using unit quaternions[J]. Journal of the Optical Society of America A, 1987, 4(4): 629–642. DOI:10.1364/JOSAA.4.000629 |
| [14] | Tian Y, Fang M. A time synchronization method for inertial sensor and visual sensor[C]//12th World Congress on Intelligent Control and Automation. Piscataway, NJ, USA: IEEE, 2016: 836-839. |
| [15] |
孙茂伟, 杨慧中.
局部加权混合核偏最小二乘算法及其在软测量中的应用[J]. 信息与控制, 2015, 44(4): 481–486.
Sun M W, Yang H Z. Local weighted mixed kernel partial least squares algorithm and its applications in to soft-sensing[J]. Information and Control, 2015, 44(4): 481–486. |
| [16] | Hearn D, Baker M P. Computer graphics:C version[M]. New Jersey, USA: Prentice-Hall, Inc, 1996: 610-662. |
| [17] | Wang H, Dan O, Verbeek J. A robust and efficient video representation for action recognition[J]. International Journal of Computer Vision, 2015, 36(2): 1–20. |
| [18] | Jia C, Sinno Z, Evans B L. Real-time 3D rotation smoothing for video stabilization[C]//Asilomar Conference on Signals, Systems and Computers. Piscataway, NJ, USA: IEEE, 2015: 673-677. |
| [19] | Chen X, Song R, Shen C, et al. Application of a genetic algorithm Elman network in temperature drift modeling for a fiber-optic gyroscope[J]. Applied Optics, 2014, 53(26): 6043–6050. DOI:10.1364/AO.53.006043 |
| [20] |
黄晨, 王建军, 高昕, 等.
电子稳像中稳像质量评价方法研究[J]. 激光与红外, 2013, 43(5): 477–481.
Huang C, Wang JJ, Gao X, et al. Study on video stabilization performance assessment inelectronic image stabilization[J]. Laser & Infrared, 2013, 43(5): 477–481. |



