0 引言
近年来,非负矩阵分解(nonnegative matrix factorization,NMF)算法在数据挖掘和机器学习领域受到越来越多的重视,在很多应用场景中发挥着作用,包括财务数据分析[1]、基因表达分析[2]、社交网络分析[3]、视觉追踪[4]、图像去噪[5]、手背静脉识别[6]、文本聚类[7]、大规模异构数据联合聚类[8].
给定非负矩阵X∈Rp×n和r<<min(p,n),NMF算法将X分解为两个非负矩阵F∈Rp×r和G∈Rr×n的乘积,其中F被称为基矩阵,G被称为系数矩阵,这样高维空间(p维)的点xi被投影到低维空间(r维)的点gi.由于非负的约束,NMF算法得到的矩阵F和G具有稀疏性,从而提供了基于局部的特征表示.
标准NMF算法[9]利用F范数(Frobenius norm)衡量矩阵分解的质量,然而数据中具有较大误差的噪音和异常值,能显著地影响目标函数值,算法的聚类性能因此下降.基于L21范数的鲁棒NMF算法[10](robust NMF using L21 norm,L21NMF算法)和基于CIM的rCIM-NMF算法[11](row-based Correntropy Induced Metric NMF,rCIM-NMF算法)克服了标准NMF算法对噪音和异常值敏感的缺点,提升了算法的鲁棒性.基于Logdet散度的稀疏NMF算法[12](Logdet divergence based sparse NMF,LDS-NMF算法)利用L21范数作为矩阵分解的误差函数,同时约束基矩阵F的秩为r,并利用L1范数正则项进一步增强系数矩阵G的稀疏性.基于线性投影结构的NMF算法[13](Linear Projection-Based NMF,LPB-NMF算法)和线性投影NMF算法[14](linear projective NMF,LP-NMF算法)将X∈Rp×n分解为基矩阵F∈Rp×r、变换矩阵Q∈Rr×p和X∈Rp×n三者的乘积.
流形是局部具有欧氏空间性质的空间,流形学习通过发现嵌入到高维空间中的低维流形,达到降维目的.流形学习算法包括等度量映射[15](Isometric mapping,Isomap),局部线性嵌入[16](locally linear embedding,LLE),拉普拉斯特征嵌入[17](Laplacian Eigenmap,LE)等,它们利用了局部不变性,即高维空间中距离近的样本点在低维流形中的距离也近.谱聚类算法[18](spectral clustering,SC算法)计算数据集的亲和矩阵,进一步得到嵌入的低维流形,再利用k均值(k-means)算法进行聚类.图正则的非负矩阵分解算法[19](graph regularized NMF,GNMF算法)通过亲和矩阵来编码数据的几何结构,构建了能反映该几何结构的NMF算法.几何结构保持的非负矩阵分解算法[20](structure preseving NMF,SPNMF算法)将近邻样本点间的相似性关系的保持和非近邻样本点间的互斥性关系的保持引入到NMF框架中.结构投影NMF算法[21](structured projective NMF,SP-NMF算法)将图正则的方法引入到投影NMF模型中.
本文提出了一种基于投影梯度方法的鲁棒流形非负矩阵分解算法(robust nonnegative matrix factorization on manifold via projected garadient method,RMPGM-NMF),该算法:
1) 使用L21范数衡量矩阵分解的质量,对数据中噪音和异常值不敏感,克服了GNMF算法和标准NMF算法中使用F范数受数据中噪音和异常值影响大的缺点;
2) 利用数据的几何结构并考虑局部不变性,将流形学习与鲁棒NMF相结合,克服了L21NMF算法,rCIM-NMF算法和LDS-NMF算法中未考虑数据内在的几何结构的缺点;
3) 利用投影梯度方法求解得到矩阵F和G的更新规则,避免了上述其它算法使用乘性更新规则时分母可能为0的情况.
1 相关NMF算法和SC算法在这个部分,简单回顾下标准NMF算法、L21NMF算法、rCIM-NMF算法、LDS-NMF算法、LP-NMF算法、SC算法和GNMF算法.输入矩阵定义为X=(x1,x2,…,xn),每个p维的列向量xi表示一个非负的数据样本.
1.1 标准NMF算法标准NMF算法利用F范数衡量X和FG的差值,定义为
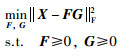
|
(1) |
其中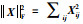
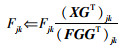
|
(2) |
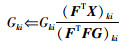
|
(3) |
L21NMF算法利用L21范数衡量矩阵分解的质量,定义为
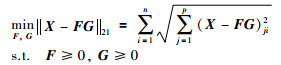
|
(4) |
其乘性更新规则为
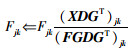
|
(5) |
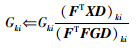
|
(6) |
其中,
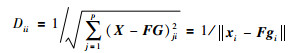
|
(7) |
rCIM-NMF算法的目标函数为
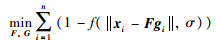
|
(8) |
其中f(e,σ)为高斯核函数:
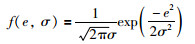
|
(9) |
其乘性更新规则为
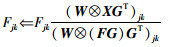
|
(10) |
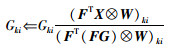
|
(11) |
其中,
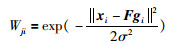
|
(12) |
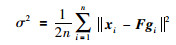
|
(13) |
LDS-NMF算法约束矩阵F的秩为r,同时引入L1正则项增强矩阵G的稀疏性,其目标函数为
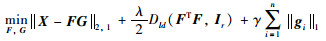
|
(14) |
其中,λ和γ为可调参数,Ir为r维的单位矩阵,Dld(A,A0)的定义为
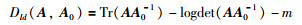
|
(15) |
其中m为方阵A的维度.
LDS-NMF算法的乘性更新规则为
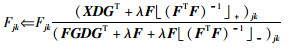
|
(16) |
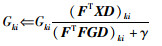
|
(17) |
其中,
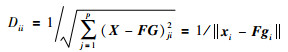
|
(18) |
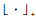
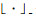
LP-NMF算法的目标函数为
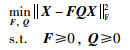
|
(19) |
其乘性更新规则为
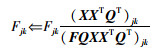
|
(20) |
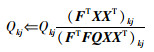
|
(21) |
SC算法首先计算亲和矩阵A∈Rn×n,
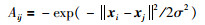
|
(22) |
再计算归一化的亲和矩阵L,
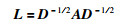
|
(23) |
其中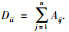
找到矩阵L的k个最大特征向量y1,y2,…,yk,构成矩阵Y=[y1,y2,…,yk]∈Rn×k,令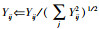
GNMF算法引入拉普拉斯矩阵L,其定义为
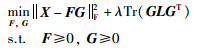
|
(24) |
其中L=V-W,W为亲和矩阵,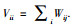
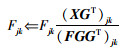
|
(25) |
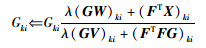
|
(26) |
这部分将给出RMPGM-NMF算法的定义,为方便求解出更新规则,本文推导出了等价的目标函数.
2.1 RMPGM-NMF算法的定义在L21NMF算法中,每个数据样本的目标函数值为
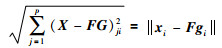
|
(27) |
而在标准NMF算法中,每个数据样本的目标函数值为
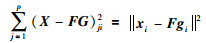
|
(28) |
数据集中存在的具有较大误差的噪音和异常值会极大地影响标准NMF算法的目标函数值(28),从而降低算法的聚类性能,而L21NMF算法的目标函数值(27)受噪音和异常值的影响较小.
结合L21NMF和流行学习,将拉普拉斯矩阵引入到L21NMF算法中,提出了RMPGM-NMF算法,该算法保证鲁棒性的同时,利用数据的几何结构并考虑局部不变性,使得高维空间X中样本的几何结构在进行矩阵分解后的低维空间G中得以保持.其定义为
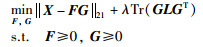
|
(29) |
其中,L=V-W,L为拉普拉斯矩阵,W为亲和矩阵,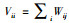
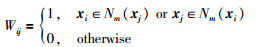
|
(30) |
其中Nm(x)表示距离数据样本x最近的m个数据样本的集合,任意两个数据样本之间的距离定义为
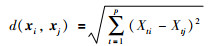
|
(31) |
直接由式(29)求解F和G的更新规则比较困难,本文将给出与式(29)等价的目标函数.
定理1 求解式(29)等价于求解式(32):
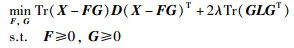
|
(32) |
其中D为对角矩阵,其对角元素为
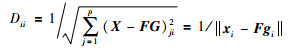
|
(33) |
证明 若求解式(32)得到更新规则:

|
(34) |

|
(35) |
使得
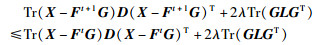
|
(36) |
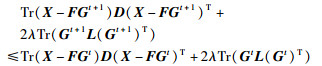
|
(37) |
文[10]中的不等式(38)和不等式(39)为
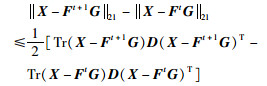
|
(38) |
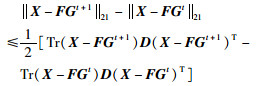
|
(39) |
由不等式(36)可得:
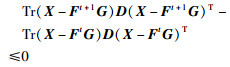
|
(40) |
将其代入到不等式(38)中可得:
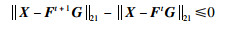
|
(41) |
则:
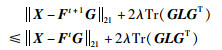
|
(42) |
由不等式(37)可得:
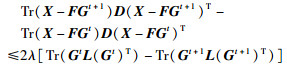
|
(43) |
将其代入到不等式(39)中可得:
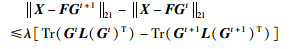
|
(44) |
则:
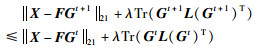
|
(45) |
不等式(42)和不等式(45)表明式(32)的更新规则(34)和(35)同样也使式(29)中目标函数值单调不递增,从而求解式(29)等价于求解式(32).
若X的某一行或者某一列全为0,乘性更新规则的分母可能为0,而使用投影梯度方法则不会遇到这样的问题.我们将在第3小节中利用投影梯度方法对式(32)进行求解.
3 RMPGM-NMF算法的更新规则在这部分,先利用投影梯度方法求解一般约束优化问题,进一步利用投影梯度方法求解RMPGM-NMF算法中F和G的更新规则.
3.1 一般约束优化问题的投影梯度方法求解一般约束优化问题的标准形式为
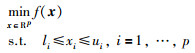
|
(46) |
其中x是一个p维的列向量.
投影梯度方法使用如下规则更新当前解xt到xt+1:
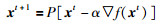
|
(47) |
其中,
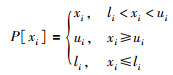
|
(48) |
不同的投影梯度方法对步长α的选择不同,算法1展示了一个简单有效的求解式(46)的投影梯度方法,每轮迭代中α的初始值设置为1(第1行),不等式(49)可以保证每轮迭代中目标函数值f(x)有足够的下降,判断不等式(49)是否成立:若成立(第4行),则不断增大α的值直至不等式(49)不成立,将α_pre代入式(47)中计算得到xt+1并返回(第5行~第11行),若不成立(第13行),则不断减小α的值直至不等式(49)成立,将α_new代入式(47)中计算得到xt+1并返回(第14行~第19行).
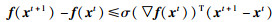
|
(49) |
算法1 式(41)的更新规则
输入:xt
输出:xt+1
BEGIN
1) α_pre=1,β=0.1,σ=0.01
2) xt+1=P[xt-α_pre▽f(xt)]
3) condition=(f(xt+1)-f(xt)≤σ(▽f(xt))T(xt+1 -xt))
4) IF (condition)
5) WHILE (condition)
6) α_new=α_pre/β
7) xt+1=P(xt-α_new▽f(xt))
8) condition=(f(xt+1)-f(xt)≤σ(▽f(xt))T(xt+1 -xt))
9) END WHILE
10) xt+1=P[xt-α_pre▽f(xt)]
11) return xt+1
12) END IF
13) ELSE
14) WHILE (! condition)
15) α_new=α_pre×β
16) xt+1=P(xt-α_new▽f(xt))
17) condition=(f(xt+1)-f(xt)≤σ(▽f(xt))T·(xt+1-xt))
18) END WHILE
19) return xt+1
20) END ELSE
END
3.2 RMPGM-NMF算法的投影梯度方法求解由第2部分的分析,求解式(29)等价于求解式(32),记:
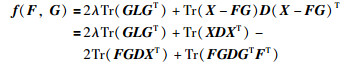
|
(50) |
则:
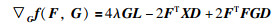
|
(51) |
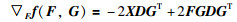
|
(52) |
于是RMPGM-NMF算法中G和F的更新规则分别如算法2和算法3所示,其中算法2中的〈▽Gtf(F,Gt),(Gt+1-Gt)〉表示两个矩阵▽Gtf(F,Gt)和Gt+1-Gt的内积,算法3中的〈▽Ftf(Ft,G),(Ft+1-Ft)〉表示两个矩阵▽Ftf(Ft,G)和Ft+1-Ft的内积,算法2和算法3中的函数P[·]定义为
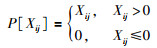
|
(53) |
算法2和算法3中最耗时的操作是式(54)的计算:
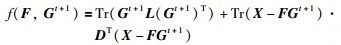
|
(54) |
在每一轮WHILE循环中(第8~12行或第17~21行),为了计算condition的值(第11行或第20行),都需要计算式(54).式(54)中等号右边第1项的浮点乘法操作数为kn2+nk2,浮点加法操作数为kn2+nk2+k,等号右边第2项的浮点乘法操作数为2pkn+pn2+np2,浮点加法操作数为2pkn +pn2 +np2 +2pn +p,则式(54)的总操作数为2pn2 +2np2+2kn2+2nk2+4pkn+2pn+p+k,因为一般k<<min(p,n),则式(54)的时间复杂度为O(pn(p+n)),记WHILE循环次数为#iterations,则算法2和算法3的时间复杂度均为#iterations×O(pn(p+n)).
算法2 update_G
输入:X,F,Gt,D,L
输出:Gt+1
BEGIN
1) α_pre=1,β=0.1,σ=0.01
2) f(F,Gt)=Tr(GtL(Gt)T)+Tr(X-FGt)D(X-FGt)T
3) f(F,Gt+1)=Tr(Gt+1L(Gt+1)T)+Tr(X-FGt+1)·D(X-FGt+1)T
4) ▽Gtf(F,Gt)=2GtL-2FTXD+2FTFGtD
5) Gt+1=P[Gt-α_pre▽Gtf(F,Gt)]
6) condition=(f(F,Gt+1)-f(F,Gt)≤σ〈▽Gtf(F,Gt),(Gt+1-Gt)〉)
7) IF (condition)
8) WHILE (condition)
9) α_new=α_pre/β
10) Gt+1=P[Gt-α_new▽Gtf(F,Gt)]
11) condition=(f(F,Gt+1)-f(F,Gt)≤σ〈▽Gtf(F,Gt),(Gt+1-Gt)〉)
12) END WHILE
13) Gt+1=P[Gt-α_pre▽Gtf(F,Gt)]
14) return Gt+1
15) END IF
16) ELSE
17) WHILE (! condition)
18) α_new=α_pre×β
19) Gt+1=P[Gt-α_new▽Gtf(F,Gt)]
20) condition=(f(F,Gt+1)-f(F,Gt)≤σ〈▽Gtf(F,Gt),(Gt+1-Gt)〉)
21) END WHILE
22) return Gt+1
23) END ELSE
END
算法3 update_F
输入:X,Ft,G,D,L
输出:Ft+1
BEGIN
1) α_pre=1,β=0.1,σ=0.01
2) f(Ft,G)=Tr(GLGT)+Tr(X-FtG)D(X-FtG)T
3) f(Ft+1,G)=Tr(GLGT)+Tr(X-Ft+1G)D(X-Ft+1G)T
4) ▽Ftf(Ft,G)=-2XDGT+2FtGDGT
5) Ft+1=P[Ft-α_pre▽Ftf(Ft,G)]
6) condition=(f(Ft+1,G)-f(Ft,G)≤σ〈▽Ftf(Ft,G),(Ft+1-Ft)〉)
7) IF (condition)
8) WHILE (condition)
9) α_new=α_pre/β
10) Ft+1=P[Ft-α_new▽Ftf(Ft,G)]
11) condition=(f(Ft+1,G)-f(Ft,G)≤σ〈▽Ftf(Ft,G),(Ft+1-Ft)〉)
12) END WHILE
13) Ft+1=P[Ft-α_pre▽Ftf(Ft,G)]
14) return Ft+1
15) END IF
16) ELSE
17) WHILE (! condition)
18) α_new=α_pre×β
19) Ft+1=P[Ft-α_new▽Ftf(Ft,G)]
20) condition=(f(Ft+1,G)-f(Ft,G)≤σ〈▽Ftf(Ft,G),(Ft+1-Ft)〉)
21) END WHILE
22) return Ft+1
23) END ELSE
END
4 实验本文将RMPGM-NMF算法同k-means算法、PCA算法、标准NMF算法[9]、L21NMF算法[10]、rCIM-NMF算法[11]、LDS-NMF算法[12]和LP-NMF算法[14]、SC算法[19]、GNMF算法[20]进行比较,给出聚类结果,并分析RMPGM-NMF算法的收敛性和算法的性能与参数的关系.
4.1 数据集使用了5个图片数据集(来源:http://www.vision.caltech.edu/Image_Datasets/Caltech101和http://www.cad.zju.edu.cn/home/dengcai/Data/data.html),表 1概括了这5个数据集的基本特性.对于每个数据集,本文随机选取K1个类别的样本点构成第1个子集,再从第1个子集中随机选取K2个类别的样本点构成第2个子集,各子集的类别数K1和K2见表 2.
| 数据集 | 样本数n | 特征维度p | 类别数K |
| ORL | 400 | 1 024 | 40 |
| Umist | 360 | 644 | 20 |
| COIL20 | 1 440 | 1 024 | 20 |
| Caltech | 342 | 1 014 | 19 |
| MNIST | 1 000 | 784 | 10 |
| 数据集 | K1 | K2 |
| ORL | 30 | 20 |
| Umist | 15 | 10 |
| COIL20 | 15 | 10 |
| Caltech | 8 | 5 |
| MNIST | 8 | 5 |
ORL:包含40个人的400张人脸图片,它们拍摄于不同的时间、不同的光线条件且同一个人的多张图片中面部表情也不同.每张图片被裁剪为32×32像素.
Umist:包含20个人的360张人脸图片,同一个人的18张图片差别很大,因此在人脸识别时具有挑战性.每张图片的像素为28×23.
COIL20:包含1 440张图片,分别属于20个类别,每个类别有72张图片,每张图片中的物体处于不同的角度.每张图片的分辨率为32×32像素.
Caltech:Caltech101中的图片可以划分为101个大类,其中"人脸"类中包含了435张人脸图片,我们从中选取了19个人的共342张图片,平均每个人18张图片,每张图片被裁剪为39×26像素.
MNIST:该数据集包含手写的数字"0"到"9"的共70 000张图片,从每个类别中随机选取了100张图片,因此实验中使用的MNIST数据集样本数为1 000.每张图片裁剪为28×28像素.
4.2 性能指标本文使用的性能指标包括聚类准确度ACC(clustering accuracy),归一化的互信息NMI(normalized mutual information),纯度PUR(purity).
ACC定义为
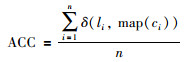
|
(55) |
li和ci分别是样本点xi的真实类标签和聚类得到的类标签,最佳匹配函数map(·)通过匈牙利算法(Hungarian algorithm)求解,函数δ(x,y)定义为
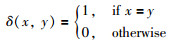
|
(56) |
ACC的值越大表示聚类性能越好.
NMI的定义为
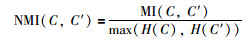
|
(57) |
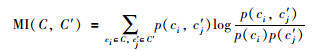
|
(58) |
其中,C表示样本真实类标签的集合,C'表示聚类得到的类标签的集合,MI(C,C')为C和C'的互信息,其中p(ci)表示任取一个样本点属于类别ci的概率,p(cj')表示任取一个样本点属于类别cj'的概率,p(ci,cj')表示任取一个样本点同时属于类别ci和cj'的概率. NMI(C,C')表示C和C'归一化的互信息,其中H(C)和H(C')分别表示C和C'的信息熵.
NMI的值越大表示聚类性能越好.
PUR的定义如下:
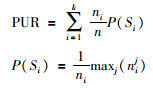
|
(59) |
其中,Si表示聚类后类别标签为i的样本点集合,ni表示该集合包含的样本点数目,nij表示真实类别标签为j的样本点聚类后标签为i的样本点数目.
PUR的值越大表示聚类性能越好.
4.3 实验结果实验中,NMF算法、L21NMF算法、rCIM-NMF算法、LDS-NMF算法、GNMF算法和RMPGM-NMF算法的矩阵F和G的初始值均为相同的随机生成的矩阵,迭代次数均为1 000,在最终得到的系数矩阵G上运行k-means算法获得聚类结果. LP-NMF算法的迭代次数为1 000次,在最终得到的矩阵QX上运行k-means算法获得聚类结果.
实验中10个算法均运行5次,并计算5次运行得到的ACC、NMI、PUR的平均值.其中每次调用k-means算法,均执行20次,返回的聚类结果使得各个样本点到其类中心的距离之和最小.
SC算法中的σ参数设置为σ2=0.5×106. LDS-NMF算法有2个可调的参数,即参数λ和γ,实验中设定λ=0.01,γ依次变化为{0.001,0.01,0.1,1,10,100,1 000};再设定γ=1,λ依次变化为{0.000 01,0.000 1,0.001,0.01,0.1,1,10}. RMPGM-NMF算法和GNMF算法中有2个可调的参数,即参数λ和构造亲和矩阵W使用的最近邻居样本点的数目m.实验中先设定λ=100,m依次变化为{3,5,7,9,11,13,15};再设定m=5,λ依次变化为{0.001,0.01,0.1,1,10,100,1 000}.不同的参数组合导致不同的聚类结果,选取最好的聚类结果衡量该算法的聚类性能.
10个算法在5个数据集及其子集上的聚类结果如表 3~表 7所示,每个算法的聚类数目r设置为各个数据集真实的类别数,即r=K或r=K1或r=K2,各性能指标的最优值用粗体显示,可以看出,RMPGM-NMF算法的性能优于其它9种算法.
| (a) ORL (r=40) | |||
| 算法 | ACC | NMI | PUR |
| k-means | 0.609 999 | 0.672 646 | 0.674 124 |
| PCA | 0.608 515 | 0.675 256 | 0.675 548 |
| NMF | 0.626 764 | 0.695 511 | 0.674 736 |
| L21NMF | 0.642 326 | 0.700 769 | 0.681 708 |
| rCIM-NMF | 0.642 715 | 0.702 743 | 0.679 083 |
| LDS-NMF | 0.667 000 | 0.804 859 | 0.713 000 |
| LP-NMF | 0.423 000 | 0.663 903 | 0.473 000 |
| SC | 0.662 000 | 0.813 943 | 0.708 500 |
| GNMF | 0.658 500 | 0.804 153 | 0.721 000 |
| RMPGM-NMF | 0.670 000 | 0.820 170 | 0.748 000 |
| (b) ORL (r=30) | |||
| 算法 | ACC | NMI | PUR |
| k-means | 0.616 667 | 0.779 404 | 0.699 333 |
| PCA | 0.625 333 | 0.788 288 | 0.713 333 |
| NMF | 0.688 667 | 0.808 494 | 0.749 333 |
| L21NMF | 0.692 667 | 0.819 218 | 0.762 000 |
| rCIM-NMF | 0.689 333 | 0.820 004 | 0.754 667 |
| LDS-NMF | 0.710 000 | 0.824 088 | 0.765 333 |
| LP-NMF | 0.448 000 | 0.658 986 | 0.498 667 |
| SC | 0.702 667 | 0.828 745 | 0.750 667 |
| GNMF | 0.700 000 | 0.813 855 | 0.752 000 |
| RMPGM-NMF | 0.720 000 | 0.851 056 | 0.806 000 |
| (c) ORL (r=20) | |||
| 算法 | ACC | NMI | PUR |
| k-means | 0.732 000 | 0.837 970 | 0.805 000 |
| PCA | 0.734 000 | 0.838 617 | 0.792 000 |
| NMF | 0.759 000 | 0.853 474 | 0.834 000 |
| L21NMF | 0.771 000 | 0.851 068 | 0.819 000 |
| rCIM-NMF | 0.770 000 | 0.850 616 | 0.815 000 |
| LDS-NMF | 0.780 000 | 0.864 621 | 0.841 000 |
| LP-NMF | 0.525 000 | 0.693 837 | 0.595 000 |
| SC | 0.775 000 | 0.868 728 | 0.840 000 |
| GNMF | 0.787 000 | 0.866 893 | 0.838 000 |
| RMPGM-NMF | 0.847 000 | 0.906 377 | 0.885 000 |
| (a) Umist (r=20) | |||
| 算法 | ACC | NMI | PUR |
| k-means | 0.442 037 | 0.653 031 | 0.533 889 |
| PCA | 0.450 370 | 0.656 191 | 0.538 704 |
| NMF | 0.419 444 | 0.589 095 | 0.492 222 |
| L21NMF | 0.438 333 | 0.599 428 | 0.497 778 |
| rCIM-NMF | 0.470 000 | 0.620 086 | 0.521 111 |
| LDS-NMF | 0.472 222 | 0.621 749 | 0.515 556 |
| LP-NMF | 0.436 111 | 0.637 092 | 0.523 889 |
| SC | 0.460 556 | 0.655 468 | 0.533 333 |
| GNMF | 0.455 556 | 0.613 493 | 0.509 444 |
| RMPGM-NMF | 0.543 889 | 0.717 442 | 0.613 889 |
| (b) Umist (r=15) | |||
| 算法 | ACC | NMI | PUR |
| k-means | 0.474 815 | 0.662 507 | 0.550 370 |
| PCA | 0.478 519 | 0.657 235 | 0.562 963 |
| NMF | 0.455 556 | 0.593 874 | 0.517 037 |
| L21NMF | 0.469 630 | 0.602 600 | 0.523 704 |
| rCIM-NMF | 0.470 370 | 0.602 766 | 0.522 222 |
| LDS-NMF | 0.494 815 | 0.622 266 | 0.543 704 |
| LP-NMF | 0.482 222 | 0.655 539 | 0.541 481 |
| SC | 0.518 519 | 0.667 101 | 0.582 963 |
| GNMF | 0.471 111 | 0.593 969 | 0.525 926 |
| RMPGM-NMF | 0.553 333 | 0.702 558 | 0.610 370 |
| (c) Umist (r=10) | |||
| 算法 | ACC | NMI | PUR |
| k-means | 0.523 333 | 0.640 506 | 0.584 444 |
| PCA | 0.537 778 | 0.642 834 | 0.588 889 |
| NMF | 0.488 889 | 0.528 526 | 0.535 556 |
| L21NMF | 0.503 333 | 0.533 981 | 0.537 778 |
| rCIM-NMF | 0.511 111 | 0.547 435 | 0.536 667 |
| LDS-NMF | 0.518 889 | 0.555 309 | 0.544 444 |
| LP-NMF | 0.503 333 | 0.621 707 | 0.600 000 |
| SC | 0.507 778 | 0.614 395 | 0.581 111 |
| GNMF | 0.503 333 | 0.542 083 | 0.544 444 |
| RMPGM-NMF | 0.586 667 | 0.669 900 | 0.630 000 |
| (a) COIL20 (r=20) | |||
| 算法 | ACC | NMI | PUR |
| k-means | 0.658 610 | 0.654 543 | 0.714 756 |
| PCA | 0.657 244 | 0.653 401 | 0.715 308 |
| NMF | 0.619 088 | 0.596 687 | 0.660 042 |
| L21NMF | 0.621 000 | 0.597 024 | 0.653 343 |
| rCIM-NMF | 0.624 150 | 0.601 529 | 0.658 886 |
| LDS-NMF | 0.668 472 | 0.765 234 | 0.713 472 |
| LP-NMF | 0.668 889 | 0.774 894 | 0.744 861 |
| SC | 0.690 972 | 0.791 420 | 0.730 417 |
| GNMF | 0.801 111 | 0.893 579 | 0.882 639 |
| RMPGM-NMF | 0.835 556 | 0.900 284 | 0.889 722 |
| (b) COIL20 (r=15) | |||
| 算法 | ACC | NMI | PUR |
| k-means | 0.697 407 | 0.773 888 | 0.771 111 |
| PCA | 0.635 370 | 0.761 675 | 0.757 407 |
| NMF | 0.680 926 | 0.744 706 | 0.735 741 |
| L21NMF | 0.690 926 | 0.754 662 | 0.741 481 |
| rCIM-NMF | 0.679 259 | 0.747 582 | 0.723 333 |
| LDS-NMF | 0.708 704 | 0.769 151 | 0.747 778 |
| LP-NMF | 0.679 074 | 0.774 144 | 0.773 889 |
| SC | 0.698 333 | 0.782 390 | 0.742 963 |
| GNMF | 0.807 593 | 0.881 751 | 0.865 000 |
| RMPGM-NMF | 0.907 037 | 0.938 679 | 0.931 852 |
| (c) COIL20 (r=10) | |||
| 算法 | ACC | NMI | PUR |
| k-means | 0.762 500 | 0.791 538 | 0.820 556 |
| PCA | 0.768 611 | 0.793 080 | 0.818 611 |
| NMF | 0.738 611 | 0.760 358 | 0.791 944 |
| L21NMF | 0.728 056 | 0.759 283 | 0.778 611 |
| rCIM-NMF | 0.728 333 | 0.758 704 | 0.796 667 |
| LDS-NMF | 0.753 333 | 0.774 184 | 0.795 000 |
| LP-NMF | 0.763 056 | 0.790 694 | 0.819 444 |
| SC | 0.754 444 | 0.783 083 | 0.792 500 |
| GNMF | 0.863 611 | 0.912 608 | 0.928 611 |
| RMPGM-NMF | 0.936 667 | 0.949 331 | 0.946 667 |
| (a) Caltech (r=19) | |||
| 算法 | ACC | NMI | PUR |
| k-means | 0.481 871 | 0.570 266 | 0.518 713 |
| PCA | 0.487 135 | 0.577 609 | 0.538 012 |
| NMF | 0.632 054 | 0.700 340 | 0.678 268 |
| L21NMF | 0.644 504 | 0.706 348 | 0.684 314 |
| rCIM-NMF | 0.643 412 | 0.704 143 | 0.679 524 |
| LDS-NMF | 0.679 532 | 0.737 415 | 0.722 807 |
| LP-NMF | 0.426 316 | 0.529 948 | 0.479 532 |
| SC | 0.490 058 | 0.581 029 | 0.528 655 |
| GNMF | 0.676 608 | 0.740 467 | 0.716 374 |
| RMPGM-NMF | 0.681 287 | 0.754 257 | 0.725 731 |
| (b) Caltech (r=8) | |||
| 算法 | ACC | NMI | PUR |
| k-means | 0.651 389 | 0.687 190 | 0.701 389 |
| PCA | 0.648 611 | 0.686 771 | 0.701 389 |
| NMF | 0.748 611 | 0.722 376 | 0.772 222 |
| L21NMF | 0.761 111 | 0.743 954 | 0.783 333 |
| rCIM-NMF | 0.734 722 | 0.723 013 | 0.768 056 |
| LDS-NMF | 0.797 222 | 0.786 571 | 0.809 722 |
| LP-NMF | 0.622 222 | 0.629 731 | 0.672 222 |
| SC | 0.659 722 | 0.641 432 | 0.715 278 |
| GNMF | 0.748 611 | 0.722 376 | 0.772 222 |
| RMPGM-NMF | 0.804 167 | 0.791 972 | 0.812 500 |
| (c) Caltech (r=5) | |||
| 算法 | ACC | NMI | PUR |
| k-means | 0.644 444 | 0.496 633 | 0.722 222 |
| PCA | 0.644 444 | 0.496 633 | 0.722 222 |
| NMF | 0.755 556 | 0.667 479 | 0.806 667 |
| L21NMF | 0.793 333 | 0.700 978 | 0.808 889 |
| rCIM-NMF | 0.791 111 | 0.707 173 | 0.822 222 |
| LDS-NMF | 0.837 778 | 0.767 034 | 0.837 778 |
| LP-NMF | 0.633 333 | 0.466 669 | 0.697 778 |
| SC | 0.666 667 | 0.531 275 | 0.755 556 |
| GNMF | 0.764 444 | 0.672 660 | 0.811 111 |
| RMPGM-NMF | 0.855 556 | 0.784 835 | 0.855 556 |
| (a) MNIST (r=10) | |||
| 算法 | ACC | NMI | PUR |
| k-means | 0.523 967 | 0.534 673 | 0.591 233 |
| PCA | 0.523 967 | 0.540 301 | 0.599 800 |
| NMF | 0.506 933 | 0.501 868 | 0.560 433 |
| L21NMF | 0.509 900 | 0.496 862 | 0.549 000 |
| rCIM-NMF | 0.489 400 | 0.492 253 | 0.541 300 |
| LDS-NMF | 0.569 333 | 0.566 735 | 0.618 667 |
| LP-NMF | 0.573 333 | 0.571 110 | 0.641 333 |
| SC | 0.576 000 | 0.620 492 | 0.682 667 |
| GNMF | 0.628 000 | 0.625 722 | 0.681 333 |
| RMPGM-NMF | 0.648 000 | 0.629 136 | 0.678 667 |
| (b) MNIST (r=8) | |||
| 算法 | ACC | NMI | PUR |
| k-means | 0.586 667 | 0.559 341 | 0.653 333 |
| PCA | 0.581 667 | 0.550 404 | 0.656 667 |
| NMF | 0.610 000 | 0.605 900 | 0.686 667 |
| L21NMF | 0.586 667 | 0.571 397 | 0.651 667 |
| rCIM-NMF | 0.590 000 | 0.569 504 | 0.660 000 |
| LDS-NMF | 0.563 333 | 0.544 917 | 0.626 667 |
| LP-NMF | 0.541 667 | 0.531 892 | 0.631 667 |
| SC | 0.533 333 | 0.569 741 | 0.675 000 |
| GNMF | 0.615 000 | 0.606 642 | 0.688 333 |
| RMPGM-NMF | 0.653 333 | 0.641 588 | 0.730 000 |
| (c) MNIST (r=5) | |||
| 算法 | ACC | NMI | PUR |
| k-means | 0.693 333 | 0.649 326 | 0.720 000 |
| PCA | 0.685 333 | 0.651 752 | 0.720 000 |
| NMF | 0.661 333 | 0.630 533 | 0.797 333 |
| L21NMF | 0.765 333 | 0.664 085 | 0.784 000 |
| rCIM-NMF | 0.760 000 | 0.678 490 | 0.778 667 |
| LDS-NMF | 0.781 333 | 0.679 238 | 0.781 333 |
| LP-NMF | 0.672 000 | 0.636 051 | 0.762 667 |
| SC | 0.640 000 | 0.663 010 | 0.773 333 |
| GNMF | 0.677 333 | 0.625 084 | 0.797 333 |
| RMPGM-NMF | 0.784 000 | 0.685 890 | 0.789 333 |
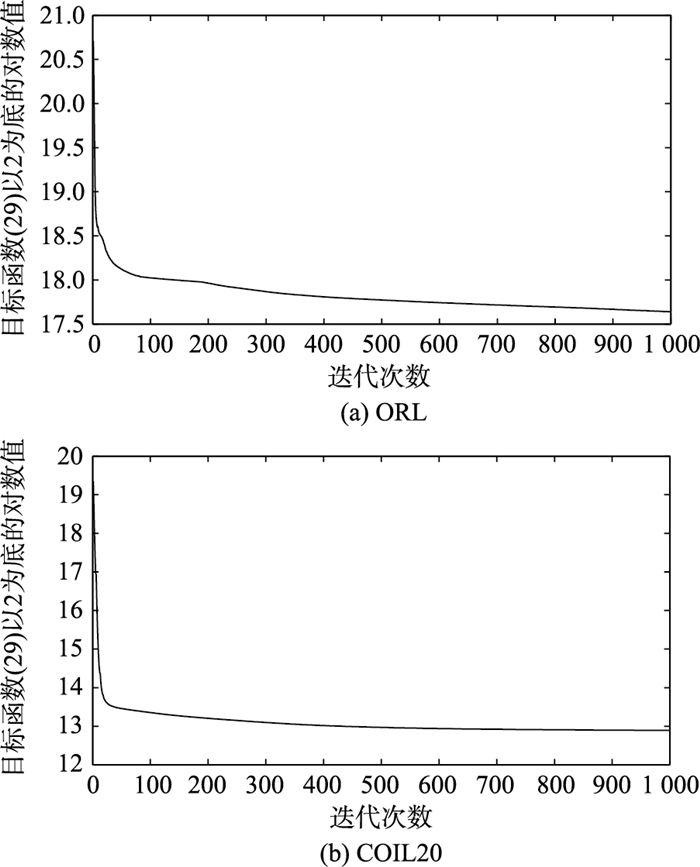
分析RMPGM-NMF算法的收敛性,以数据集ORL和COIL20为例,结果如图 1所示,横坐标为迭代的次数,纵坐标为目标函数(29)的以2为底的对数值,算法参数设置为m=5,λ=100,F和G的初始值随机生成. 图 1显示RMPGM-NMF算法可以快速收敛.
|
| 图 1 RMPGM-NMF算法的收敛性 Figure 1 The convergence of RMPGM-NMF |
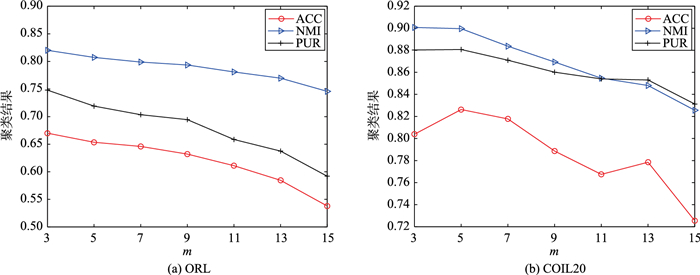
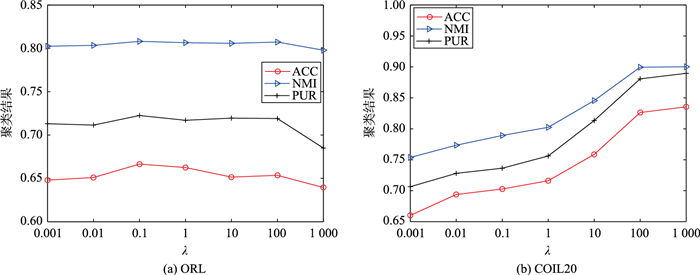
RMPGM-NMF算法有2个可调的参数m和λ,以数据集ORL和COIL20为例,图 2和图 3分别显示了RMPGM-NMF算法的性能随参数m和λ变化的情况.
|
| 图 2 RMPGM-NMF算法性能与参数m的关系 Figure 2 The relationship between the performance of RMPGM-NMF and the parameter m |
|
| 图 3 RMPGM-NMF算法性能与参数λ的关系 Figure 3 The relationship between the performance of RMPGM-NMF and the parameter λ |
图 2中λ=100,m依次变化为{3,5,7,9,11,13,15},可以看出RMPGM-NMF算法的性能随着m的增大而呈下降的趋势,这是因为本文使用m近邻的亲和矩阵刻画数据集的几何结构,即任一样本点只与其最近的m个样本点建立邻接关系,显然随着m的增大,这样建立的亲和矩阵的不合理性增大.当m取值为3~7时,RMPGM-NMF算法的性能较优.
图 3中m=5,λ依次变化为{0.001,0.01,0.1,1,10,100,1 000},可以看出对于数据集ORL,RMPGM-NMF算法的性能随着λ的变化基本稳定,对于数据集COIL20,当λ取值过小(小于0.1)时会导致RMPGM-NMF算法的性能降低.总体上,当λ取值为0.1~100时RMPGM-NMF算法的性能受λ的影响不大.
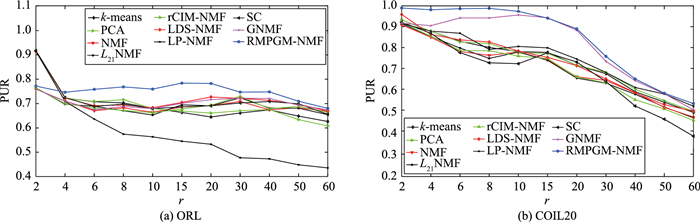
4.6 聚类数目r的分析在4.3节中,聚类数目r设置为各个数据集真实的类别数,在本节中分析RMPGM-NMF算法的性能随聚类数目r变化的情况,以数据集ORL和COIL20为例,它们的真实类别数K分别为40和20,r依次变化为{2,4,6,8,10,15,20,30,40,50,60},以PUR为衡量算法性能的指标,图 4显示随着r的变化,除了数据集ORL上r=2时,RMPGM-NMF算法的性能均优于其它算法.
|
| 图 4 RMPGM-NMF算法性能与聚类数目r的关系 Figure 4 The relationship between the performance of RMPGM-NMF and the clustering number r |
本文提出了RMPGM-NMF算法,它是基于L21范数的鲁棒流形NMF算法,利用L21范数衡量矩阵分解的质量,降低了噪音和异常值对算法聚类性能的影响,同时引入了拉普拉斯矩阵,利用数据的几何结构并考虑局部不变性,使得低维空间G能反映高维空间X中样本的几何结构,进一步提升了算法的聚类性能.本文使用了投影梯度方法求解出基矩阵F和系数矩阵G的更新规则,分析了算法的时间复杂度.在5个数据集及其子集上运行了RMPGM-NMF算法,并与k-means算法、PCA算法、SC算法、标准NMF算法及其它5种NMF相关算法进行了比较,表明了RMPGM-NMF算法的性能优于其它算法,同时分析了RMPGM-NMF算法的收敛性和算法的性能随参数m、λ及聚类数目r变化的情况.如何将RMPGM-NMF算法扩展到半监督聚类是下一步研究的重点.
| [1] | Drakakis K, Rickard S, Frein R D, et al. Analysis of financial data using nonnegative matrix factorization[J]. International Mathematical Forum, 2008, 3(38): 1853–1870. |
| [2] | Brunet J P, Tamayo P, Golub T, et al. Metagenes and molecular pattern discovery using matrix factorization[J]. Proceedings of the National Academy of Sciences, 2004, 101: 4164–4169. DOI:10.1073/pnas.0308531101 |
| [3] |
王萌萌, 左万利, 王英.
一种基于加权非负矩阵分解的多维用户人格特质识别算法[J]. 计算机学报, 2016, 39(12): 2562–2577.
Wang M M, Zuo W L, Wang Y. A multidimensional personality traits recognition model based on weighted nonnegative matrix factorization[J]. Chinese Journal of Computers, 2016, 39(12): 2562–2577. DOI:10.11897/SP.J.1016.2016.02562 |
| [4] | Wu Y, Shen B, Ling H. Visual tracking via online nonnegative matrix factorization[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2014, 24(3): 374–383. DOI:10.1109/TCSVT.2013.2278199 |
| [5] | Ye M, Qian Y, Zhou J. Multitask sparse nonnegative matrix factorization for joint spectral-spatil hyperspectral imagery denoising[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(5): 2621–2639. DOI:10.1109/TGRS.2014.2363101 |
| [6] |
贾旭, 崔建江, 孙福明, 等.
基于改进非负矩阵分解的手背静脉识别算法[J]. 信息与控制, 2016, 45(2): 193–198.
Jia X, Cui J J, Sun F M, et al. Dorsal hand vein recognition algorithm based on improved nonnegative matrix factorization[J]. Information and Control, 2016, 45(2): 193–198. |
| [7] | Kuang D, Park H. Fast rank-2 nonnegative matrix factorization for hierarchical document clustering[C]//Proceedings of the 19th ACM international conference on knowledge discovery and data mining. New York, USA: ACM, 2013: 739-747. |
| [8] |
申国伟, 杨武, 王巍, 等.
基于非负矩阵分解的大规模异构数据联合聚类[J]. 计算机研究与发展, 2016, 53(2): 459–466.
Shen G W, Yang W, Wang W, et al. Large-scale heterogeneous data co-clustering based on nonnegative matrix factorization[J]. Journal of Computer Research and Development, 2016, 53(2): 459–466. DOI:10.7544/issn1000-1239.2016.20148284 |
| [9] | Lee D D, Seung H S. Algorithms for nonnegative matrix factorization[M]. Berlin, Germany: Springer, 2001: 556-562. |
| [10] | Kong D, Ding C, Huang H. Robust nonnegative matrix factorization using L12-norm[C]//Proceeding of the 20th ACM Conference on Information and Knowledge Management. New York, NY, USA: ACM, 2011: 673-682. |
| [11] | Du L, Li X, Shen Y D. Robust nonnegative matrix factorization via half-quadratic minimization[C]//Proceedings of the 12th IEEE International Conference on Data Mining. Piscataway, NJ, USA: IEEE, 2012: 201-210. |
| [12] | Liao Q, Guan N, Zhang Q. Logdet divergence based sparse non-negative matrix factorization for stable representation[C]//Proceedings of the 15th IEEE International Conference on Data Mining. Piscataway, NJ, USA: IEEE, 2015: 871-876. |
| [13] |
李乐, 章毓晋.
基于线性投影结构的非负矩阵分解[J]. 自动化学报, 2010, 36(1): 23–39.
Li L, Zhang Y J. Linear projection-based nonnegative matrix factorization using matrix analysis[J]. Acta Automation Sinica, 2010, 36(1): 23–39. |
| [14] |
胡俐蕊, 吴建国, 汪磊.
线性投影非负矩阵分解方法及应用[J]. 计算机科学, 2013, 40(10): 269–273.
Hu L R, Wu J G, Wang L. Application and method for linear projective non-negative matrix factorization[J]. Computer Science, 2013, 40(10): 269–273. DOI:10.3969/j.issn.1002-137X.2013.10.057 |
| [15] | Tenenbaum J, de Silva V, Langford J. A global geometric framework for nonlinear dimensionality reduction[J]. Science, 2000, 290(5500): 2319–2323. DOI:10.1126/science.290.5500.2319 |
| [16] | Roweis S, Saul L. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290(5500): 2323–2326. DOI:10.1126/science.290.5500.2323 |
| [17] | Belkin M, Niyogi P. Laplacian eigenmaps andspectral techniques for embedding and clustering[M]. Berlin, Germany: Springer, 2001: 585-591. |
| [18] | Ng A, Jordan M, Weiss Y. On spectral clustering:Analysis and analgorithm[M]. Berlin, Germany: Springer, 2002: 849-856. |
| [19] | Cai D, He X, Han J, et al. Graph regularized nonnegative matrix factorization for data representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(8): 548–1560. |
| [20] |
李冰锋, 唐延东, 韩志.
几何结构保持非负矩阵分解的数据表达方法[J]. 信息与控制, 2017, 46(1): 53–59, 64.
Li B F, Tang Y D, Han Z. A geometric structure preserving nonnegative matrix factorization for data representation[J]. Information and Control, 2017, 46(1): 53–59, 64. |
| [21] |
居斌, 钱沄涛, 叶敏超.
基于结构投影非负矩阵分解的协同过滤算法[J]. 浙江大学学报:工学版, 2015, 49(7): 1319–1325.
Ju B, Qian Y T, Ye M C. Collaborative filtering algorithm based on structured projective nonnegative matrix factorization[J]. Journal of Zhejiang University:Engineering Science, 2015, 49(7): 1319–1325. |



