0 引言
20世纪50年代,前苏联学者提出的变结构控制思想,是滑模控制的最初起源[1].滑模控制算法作为变结构控制的一个典型代表,相较于其它传统控制算法具有以下几个优势:
1) 滑模控制对参数扰动和匹配不确定性具有较强的鲁棒性,收敛速度快[2];
2) 相对于其它控制算法,滑模控制器设计比较简单、运算量小、工程实践性更好.
近20年来,随着滑模控制理论研究的不断深入,滑模控制已经在机器人、化工过程控制、船舶动力工程等多个领域取得了十分广泛的应用[3-5].机器人系统作为一种复杂的非线性系统,具有强耦合、非线性等特点,为了使机器人能在保障安全和稳定的前提下精确完成各种操作任务,需要设计高性能控制器.滑模控制能有效地提高机械臂的工作精度,改善鲁棒性[6-8],从而获得较好的控制效果.
滑模主要分为线性滑模和非线性滑模两大类.线性滑模能够使系统渐近收敛到平衡点.如果提高系统的控制高精度,一般需要增大控制增益,这会给系统输入带来较大负担.非线性滑模可以使系统有限时间收敛到平衡点[9-11],鲁棒性更强.但是,在实际的滑模控制设计过程中,如果考虑系统不确定性和外部干扰,采用切换控制虽然能使系统实现稳定,但"抖振"现象会给实际应用带来困难[12];采用非切换控制,无论是线性滑模还是非线性滑模,系统最终只能收敛到一个剩余集中.一般情况下,增大控制增益可以有效缩小剩余集,从而提高控制精度,增强鲁棒性.但是,较大的控制增益会使系统输入增加,"抖振"加剧,甚至导致控制器输出饱和[10].因此在改善"抖振"的同时提高系统的控制精度具有一定的现实意义.
改善"抖振"的方法有很多,当前研究的主要方法有自适应控制方法、边界层方法、连续趋近律方法、神经网络方法、模糊控制、干扰观测器方法等.文[13]提出一种基于特征模型的自适应离散滑模控制,实现柔性部件振动的快速抑制.文[14]提出了一种基于边界层的模糊滑模控制算法,在避免高频"抖振"的同时实现了电机的高精度运行.文[15]针对微电机陀螺仪提出一种全局神经网络滑模控制算法,实现系统的连续控制,改善系统动态品质.文[16]给出一种基于非线性干扰观测器的动态反演控制实现导弹飞行轨迹的精确追踪.文[17]则在理论角度设计一种高阶系统的干扰观测器结构,通过准确估计外部干扰,达到减小抖振和提高控制精度的目的.但是文[16-17]给出的干扰观测器只能实现干扰估计误差渐近收敛到0,在快速响应方面存在局限性.针对以上问题,文[18]设计了一种新型干扰观测器结构,实现干扰估计误差有限时间收敛到0,从而保证系统快速响应,避免"抖振"现象,但其不足在于该干扰观测器仅适用于1阶非线性系统,对2阶系统(例如机器人系统)并不适用.因此,针对上述干扰观测器存在的问题,本文将提出一种适用于2阶系统的新型干扰观测器结构,实现干扰的有限时间估计,并最终应用到机器人滑模控制当中,消除"抖振",实现系统的高精度控制.综上所述,本文的创新点如下:
1) 设计了一种适用于2阶非线性系统的新型干扰观测器结构,实现干扰的有限时间估计,保证系统快速响应的同时,避免"抖振"现象.
2) 根据文[19],设计一种基于干扰观测器的机械臂系统连续自适应滑模控制方法,实现了系统的高精度控制.与文[19]中机器人滑模控制算法相比,如果考虑外界扰动,本方法能显著减小系统的控制输入,克服"抖振"现象,改善了系统的动态性能.
1 问题描述针对典型的n轴机械臂系统,其动力学方程为
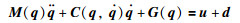
|
(1) |
其中,q=[q1,q2,…,qn]T,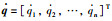
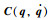
令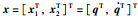
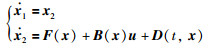
|
(2) |
其中:D(t,x)=M-1(x1)d,B(x)=M-1(x1),F(x)=-M-1(x1)[C(x1,x2)x2+G(x1)].
假设1 假设∃D > 0,使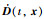
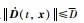
假设2 假设方程(2)状态变量都是可测的.
根据假设2,设机械臂关节角位移和角速度的期望信号分别为qd=[q1d,q2d,…,qnd]T,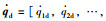
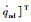
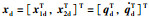
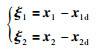
|
(3) |
本文将根据机械臂状态空间方程(2)及系统误差(3)完成干扰观测器和机械臂系统的控制律设计.
2 干扰观测器设计为简化设计和方便分析,定义符号:
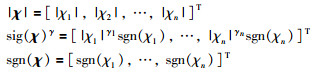
|
引理1 假设存在实数m和实数a1,a2,…,an,且0 < μ < 2,ai > 0,那么会有:
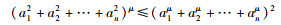
|
(4) |
外界干扰在机械臂系统中难以避免,为减少干扰对控制器性能的影响,本文设计了一种新型干扰观测器结构,实现干扰的有限时间估计.干扰观测器的结构为
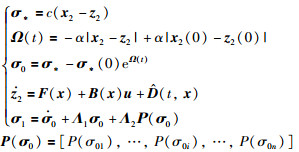
|
(5a) |
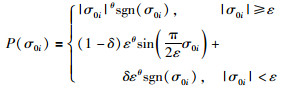
|
(5b) |
根据式(5a)设计的干扰观测器微分方程为
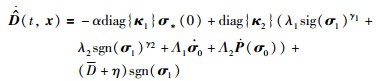
|
(6) |
其中,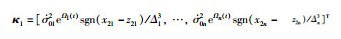
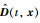
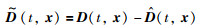
|
(7) |
定义当x2i=z2i时,Ωi(t)的导数为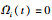
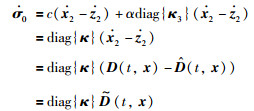
|
(8) |
其中,κ=[Δ1,…,Δn]T,κ3=[σ*1(0)eΩ1(t)sgn(x21-z21),…,σ*n(0)eΩ1(t)sgn(x2n-z2n)]T,由式(8)可得中间变量为
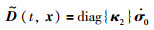
|
(9) |
进一步整理式(8)可得σ0的2阶导数表达式
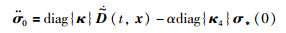
|
(10) |
其中,κ4=[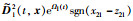
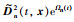
将式(9)和式(10)代入到滑模(5a)中,整理可得:
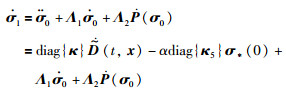
|
(11) |
其中,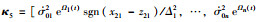
为加快系统的收敛速率使其在有限时间内收敛到滑模面σ1=0,采用文[20]给出的双次幂趋近律:
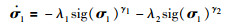
|
(12) |
将式(6)和式(12)代入式(11)整理得:
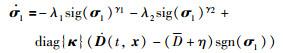
|
(13) |
定理1 如果滑模的结构如式(5a)所示,干扰观测器微分方程如式(6)所示,那么观测误差将会在有限时间内收敛到0,收敛时间T为
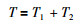
|
(14a) |
其中,
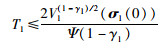
|
(14b) |
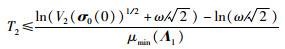
|
(14c) |
Ψ=λ12(γ1+1)/2,ω=δεθμmin(Λ2)/μmin(Λ1),μmin(Λ1)和μmin(Λ2)分别代表Λ1和Λ2的最小特征值.
证明 选李亚普诺夫函数为
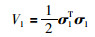
|
(15) |
对V1进行求导并代入式(13),可以得到:
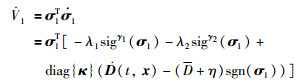
|
(16) |
考虑引理1并整理得:
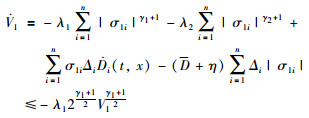
|
(17) |
令Ψ=λ12(γ1+1)/2,进一步可以得到:
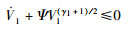
|
(18) |
解得收敛时间T1:
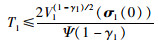
|
(19) |
由收敛时间(19)可得,系统会在有限时间内收敛到滑模面σ1=0.到达滑模面之后可以得到:
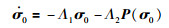
|
(20) |
证明 变量σ0会在滑模面σ1=0上有限时间收敛到0,选择李亚普诺夫函数:
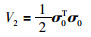
|
(21) |
对V2求导并代入式(20)可得:
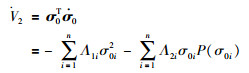
|
(22) |
由式(5b)可得不等式:
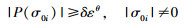
|
(23) |
当|σ0i|=0时,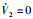
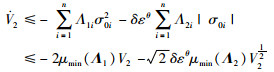
|
(24) |
解得收敛时间T2:
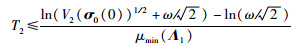
|
(25) |
其中ω,μmin(Λ1)的定义同式(14).由式(8)可得,当且仅当σ0→0,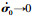
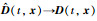
上节设计的干扰观测器能够在有限时间精确地估计系统干扰,本节将根据给出的干扰观测器,设计一种基于干扰观测器的自适应连续滑模控制方法以减小"抖振",改善鲁棒性,提高控制精度.
首先,结合式(3)定义的系统误差,定义一个线性滑模面:
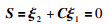
|
(26) |
其中,C=diag{C1,…,Cn},误差变量在滑模面上能实现渐近收敛到0.考虑文[19]给出的一种变增益的不连续趋近律:
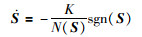
|
(27) |
其中,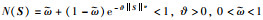
与传统的等速趋近律相比,趋近律(27)有效地缩短了收敛时间,减小抖振,但是其切换控制的本质决定了系统在收敛过程中"抖振"现象无法消除.本文在文[19]的基础上,采用自适应变增益的方法,设计一种自适应幂指数趋近律,从本质上避免"抖振",加快收敛时间.本文设计的滑模趋近律为
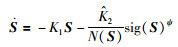
|
(28) |
自适应律设计为
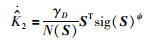
|
(29) |
其中,K1 > 0,K2 > 0,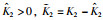
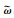
同趋近律(27)相比,新提出的自适应趋近律有效避免了不连续切换造成的"抖振"现象.自适应方法的引入使系统不断修正自身参数以适应系统状态变化,改善了系统的动态性能,提高控制精度.同时,自适应变增益会使系统在趋近过程中自发的调节收敛速度,减小控制输入.
定理2 如果滑模面设计为式(26),趋近律设计为式(28),结合滑模干扰观测器(5),基于干扰观测器的机械臂系统自适应连续滑模控制为
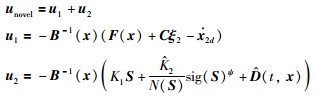
|
(30) |
那么,滑模S和系统误差ξ能够实现一致最终有界.
证明 为了证明整个系统的闭环稳定性,选择李亚普诺夫候选函数:
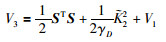
|
(31) |
其中,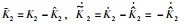
对V3求导后得到:
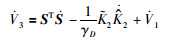
|
(32) |
考虑滑模面(26)和设计的控制律(30),可得:
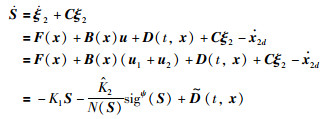
|
(33) |
根据设计的干扰观测器可知,干扰估计误差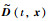
假设3 假设干扰观测器的估计误差是有界的,且满足关系式:

|
(34) |
其中,0 < γ < 1,K2和N(S)定义同(28).由引理2可知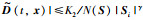
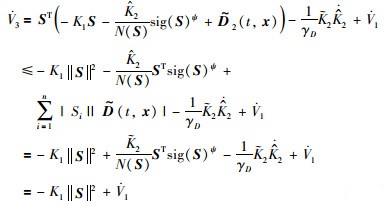
|
(35) |
根据不等式(35)得,滑模S和系统误差ξ一致最终有界,证毕.
4 仿真分析考虑2轴平面机械臂系统,动力学方程为
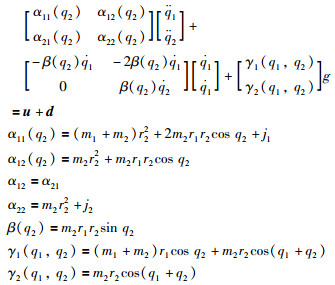
|
采用本文提出的控制律(31),控制参数为:m1=0. 5 kg,m2=1. 5 kg,r1=1 kg,r2=0. 5 kg,g=9. 8 N/s2,j1=j2=5 kg·m,C=diag{3,3},K1=1,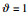
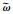
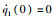
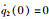
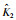
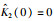
|
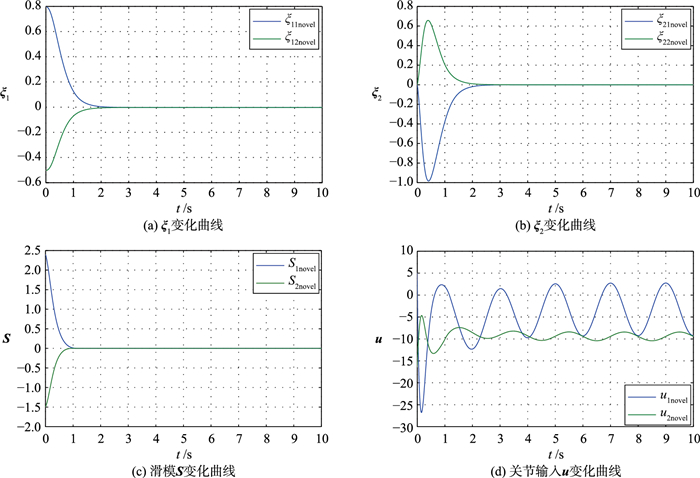
| 图 1 基于连续滑模控制的机械臂系统状态响应曲线 Figure 1 The state response curves of manipulator systems based on the continuous sliding mode control |
|
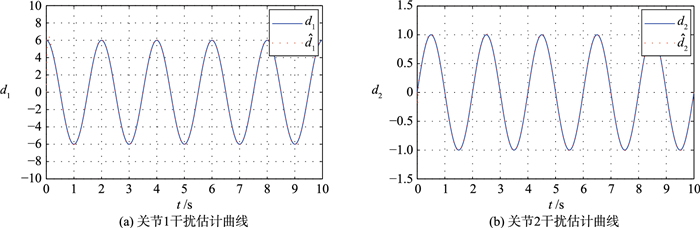
| 图 2 干扰观测器干扰逼近曲线 Figure 2 Approach curves of disturbance of disturbance observer |
|
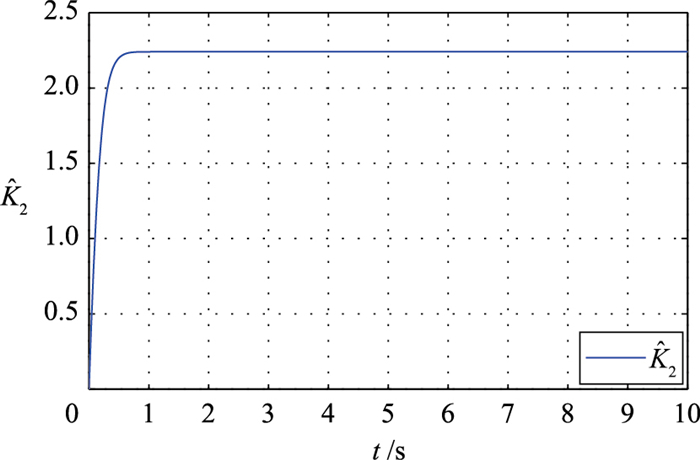
图 3 自适应参数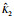 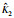 |
从图 1(a)和图 1(b)中可得,采用基于干扰观测器的自适应连续滑模控制,机械臂位置误差能够渐近收敛到平衡点.具体而言,从图 1(c)可以看出,系统首先在有限时间内收敛到线性滑模面S1=0和S2=0,收敛时间分别为t1=1. 1 s和t2=0. 9 s.到达滑模面后,系统状态将沿着滑模面渐近收敛到0.由于控制律(30)为连续滑模控制,整个收敛过程中,系统没有发生"抖振"现象,机械臂控制输入的连续性也可以在图 1(d)得到验证.
综合图 1(a)~图 1(c)和图 2可得,虽然外界存在较大干扰,但是系统误差和滑模并没有发生较大波动,控制精度较高,这得益于干扰观测器能够在有限时间内准确地估计出外在干扰,对系统输入形成补偿,减小了干扰对系统影响,提高了控制精度. 图 3给出的是自适应参数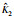
为了方便比较,本文引入文[19]给出的机械臂系统滑模切换控制:
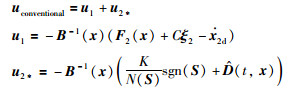
|
(36) |
由图 3中可得自适应参数的稳定估计值为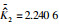
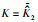
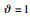
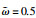
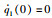
|
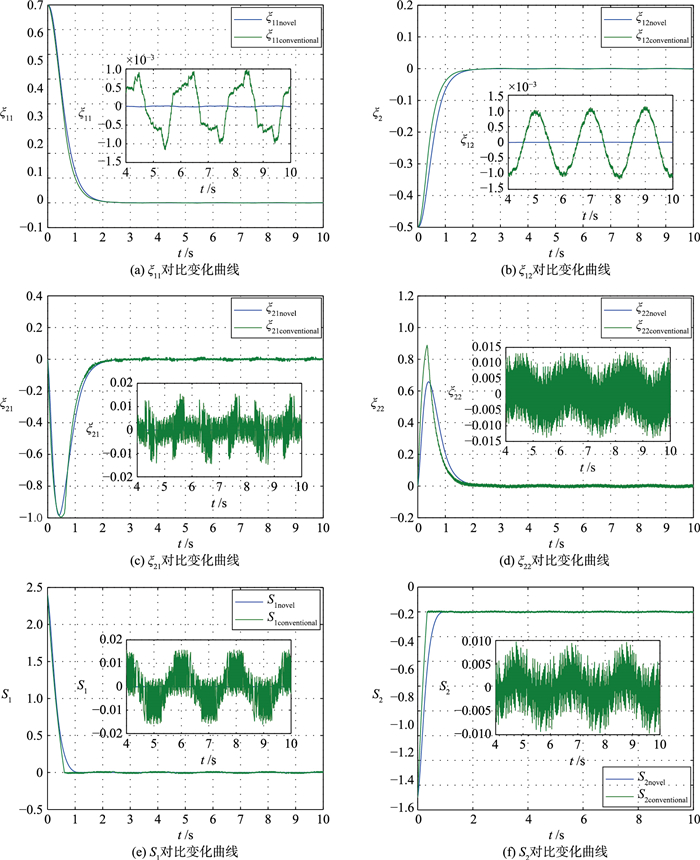
| 图 4 基于连续和不连续滑模控制的机械臂状态响应曲线 Figure 4 The state response curves of manipulator systems based on continuous and discontinuous sliding mode control |
|
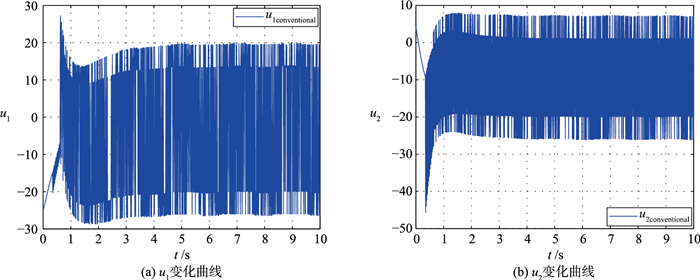
| 图 5 基于不连续滑模控制的机械臂输入时间响应曲线 Figure 5 Time response curves of control inputs of manipulator systems based on discontinuous sliding mode control |
图 4给出的是文[19]和本文方法的系统状态对比结果.首先,由图 4可以看出,基于干扰观测器的自适应连续滑模控制方法大大提高了机械臂系统的控制精度,干扰观测器的补偿作用能大大减小外界干扰对系统的影响,结合连续控制,误差变量和滑模的"抖振"现象被完全克服,系统鲁棒性得到显著改善.同时,由图 1(d)和图 5可以看出,与传统的不连续控制相比,自适应方法虽然增加了系统在趋近阶段的收敛时间,但是,自适应参数的变化能避免机械臂伺服电机在启动阶段启动力矩过大的问题,减小控制输入,改善了系统动态性能.综上所述,本文提出的基于干扰观测器的机械臂自适应连续滑模控制方法取得的效果是令人满意的.
5 结论本文针对机械臂系统高精度控制,研究了一类存在外部干扰条件下的机械臂滑模控制方法.为了改善机械臂系统的鲁棒性,避免"抖振",提高控制精度.本文设计了一种基于干扰观测器系统的自适应连续滑模控制方法.其中,干扰观测器能够有限时间精确估计外部干扰,并对系统输入进行补偿,提高控制精度,避免"抖振".自适应滑模控制方法使控制参数能够自动的随系统状态变化而变化,改善了系统的动态性能,减小控制输入.最终,通过仿真表明,该方法能有效的克服系统外在干扰,大幅提高系统的控制精度,消除"抖振现象",改善系统的动态性能.
| [1] |
梅红, 王勇.
快速收敛的机器人滑模变结构控制[J]. 信息与控制, 2009, 38(5): 552–557.
Mei H, Wang Y. Fast convergent sliding mode variable structure control of robot[J]. Information and Control, 2009, 38(5): 552–557. |
| [2] |
黄国勇.
基于神经网络干扰观测器的Terminal滑模控制[J]. 吉林大学学报:工学版, 2011, 41(6): 1726–1730.
Huang G Y. Terminal sliding mode control based on neural network disturbance observer[J]. Journal of Jilin University:Engineering and Technology Edition, 2011, 41(6): 1726–1730. |
| [3] | Islam S, Liu X P. Robust sliding mode control for robot manipulators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(6): 2444–2453. DOI:10.1109/TIE.2010.2062472 |
| [4] | Zhao D, Zhu Q, Dubbeldam J. Terminal sliding mode control for continuous stirred tank reactor[J]. Chemical Engineering Research and Design, 2015, 94: 266–274. DOI:10.1016/j.cherd.2014.08.005 |
| [5] | Perera L P, Soares C G. Pre-filtered sliding mode control for nonlinear ship steering associated with disturbances[J]. Ocean Engineering, 2012, 51: 49–62. DOI:10.1016/j.oceaneng.2012.04.014 |
| [6] | Van M, Franciosa P, Ceglarek D. Fault diagnosis and fault-tolerant control of uncertain robot manipulators using high-order sliding mode[J]. Mathematical Problems in Engineering, 2016, 2016: ID 7926280. |
| [7] | Zhao D, Zhu Q, Li N, et al. Synchronized control with neuro-agents for leader-follower based multiple robotic manipulators[J]. Neurocomputing, 2014, 124: 149–161. DOI:10.1016/j.neucom.2013.07.016 |
| [8] | Khireddine M S, Boutarfa A. Fault tolerant control on robotic manipulator using sliding mode observers[C]//International Conference on Computer Applications Technology. Piscataway, NJ, USA: IEEE, 2013: 1-6. |
| [9] | Levant A. Principles of 2-sliding mode design[J]. Automatica, 2007, 43(4): 576–586. DOI:10.1016/j.automatica.2006.10.008 |
| [10] | Kao Y G, Wang C H, Xie J, et al. H∞sliding mode control for uncertain neutral-type stochastic systems with Markovian jumping parameters[J]. Information Sciences, 2015, 314: 200–211. DOI:10.1016/j.ins.2015.03.047 |
| [11] | Zhang X, Su H, Lu R. Second-order integral sliding mode control for uncertain systems with control input time delay based on singular perturbation approach[J]. IEEE Transactions on Automatic Control, 2015, 60(11): 3095–3100. DOI:10.1109/TAC.2015.2411991 |
| [12] |
靳宝全, 熊诗波, 程珩.
电液位置伺服系统的变速趋近律滑模控制抖振抑制[J]. 机械工程学报, 2013, 49(10): 163–169.
Jin B Q, Xiong S B, Cheng H. Chattering inhibition of variable rate reaching law sliding mode control for electro-hydraulic position servo system[J]. Chinese Journal of Mechanical Engineering, 2013, 49(10): 163–169. |
| [13] |
钟华, 潘金文, 王永.
一种基于特征模型的自适应离散滑模控制[J]. 信息与控制, 2015, 44(1): 56–61.
Zhong H, Pan J W, Wang Y. Characteristic model-based adaptive discrete-time sliding mode control[J]. Information and Control, 2015, 44(1): 56–61. |
| [14] | Saghafinia A, Ping H W, Uddin M N. Fuzzy sliding mode control based on boundary layer theory for chattering-free and robust induction motor drive[J]. The International Journal of Advanced Manufacturing Technology, 2014, 71(1/2/3/4): 57–68. |
| [15] | Chu Y, Fei J. Adaptive global sliding mode control for MEMS gyroscope using RBF neural network[J]. Mathematical Problems in Engineering, 2015, 2015(1): 1–9. |
| [16] | Chen W H. Nonlinear disturbance observer-enhanced dynamic inversion control of missiles[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(1): 161–166. DOI:10.2514/2.5027 |
| [17] | Yang J, Li S, Yu X. Sliding-mode control for systems with mismatched uncertainties via a disturbance observer[J]. IEEE Transactions on Industrial Electronics, 2013, 60(1): 3988–3993. |
| [18] | Chen M, Yu J. Disturbance observer-based adaptive sliding mode control for near-space vehicles[J]. Nonlinear Dynamics, 2015, 82(4): 1671–1682. DOI:10.1007/s11071-015-2268-x |
| [19] | Fallaha C J, Saad M, Kanaan H Y, et al. Sliding-mode robot control with exponential reaching law[J]. IEEE Transactions on Industrial Electronics, 2011, 58(2): 600–610. DOI:10.1109/TIE.2010.2045995 |
| [20] |
张合新, 范金锁, 孟飞, 等.
一种新型滑模控制双幂次趋近律[J]. 控制与决策, 2013, 28(2): 289–293.
Zhang H X, Fan J S, Meng F, et al. A new double power reaching law for sliding mode control[J]. Control and Decision, 2013, 28(2): 289–293. |



