0 引言
随着科技和自动化水平的提高,工业生产过程越来越趋近复杂化,这使得提高控制系统稳定性,保证生产过程安全性和可靠性变得尤为重要.近年来,故障检测技术不断发展,广泛应用于生产过程监视.基于数据驱动的故障检测技术受到学术界的广泛关注,以PCA(principal components analysis)和PLS(partial least squares)为代表的多元统计分析方法迅速发展,衍生出多种新的故障检测方法[1-4].
化工生产过程作为工业生产的重要领域之一,越来越体现出非线性的特点,如何提取出生产过程中原始数据的有效信息对非线性过程进行监视成为故障检测技术研究的重要内容.王等[5]针对工业生产过程数据大多具有动态和非线性的特性,提出了一种多动态核主元分析(kernel principal component analysis,KPCA)的检测方法,该方法突破了KPCA单模型、非动态的建模方式,构造了适合批量生产过程的多模型、非线性和动态的建模方法.许等[6]提出了改进多尺度核主元分析法,先利用小波变换分析测量数据的多尺度特性,然后采用核主元分析算法进行在线故障检测,对检测到的故障采用核函数梯度算法实现在线故障诊断.Zhao等[7]提出了改进的特征向量选择的核主元分析(feature vector selection-kernel principal component analysis,FVS-KPCA)用于TE过程的故障检测算法,降低了运算复杂度,提高了系统的故障检测性能.核主元分析法在参数设置上都具有盲目性,针对这一点,魏等[8]提出了应用粒子群优化算法优化核函数参数,并将核主元分析应用于特征提取中.Xiao等[9]提出了核主元分析—独立元分析(kernel principal component analysis-independent component analysis,KPCA-ICA)的方法,利用KPCA对非线性数据进行降维,再利用独立成分分析(independent component analysis,ICA)的方法提取特征信息,有效地对非线性数据进行了处理.为了能够加快提取数据的特征信息,Annie等[10]又提出了块增量核主元分析(chunk incremental kernel principal component analysis,CIKPCA).但上述方法在对数据进行处理时均只保留了样本的全局信息,造成局部信息的丢失.因此,寻找可以保留原始数据邻域结构的方法开始得到学术界的关注.He等[11]为了研究数据的局部特征,保持原始数据的邻域信息,提出了邻域保持嵌入(neigh-borhood preserving embedding,NPE)方法.该方法有效地保持了数据的局部结构.Hu等[12]提出了局部保持投影算法(locality preserving projections,LPP),保留了数据的局部信息,更好地对其进行监测.Cai和He又提出正交局部保持投影[13],在LPP的基础上增加一个正交化的约束条件,通过迭代计算得到相互正交的投影方向.He等[14]为了更好地提取非线性数据的局部高斯特征,提出了统计局部保持投影(statistics locality preserving projections,SLPP)方法,应用统计模式分析(statistics pattern analysis,SPA)方法获取非高斯统计特性,再应用LPP方法来保持数据的局部流形结构.Jiang等[15]提出了具有局部保持投影的锚图方法(anchorgraph with locality preserving projection,AGLPP),试图通过重估数据点之间的关系,打破传统LPP方法存储和计算的限制.Cai和He提出了正交局部保持投影,在LPP的基础上增加了一个正交化的约束条件,通过迭代计算得到相互正交的投影方向[16].
Luo等[17]将局部算法应用于非线性生产过程提出了核局部保持投影(kernel locality preserving projections,KLPP)算法,提高了检测效果.但KLPP方法主要是通过高斯核函数将非线性数据投影到高维空间,然后再利用LPP的方法进行检测,检测效果受到核函数中参数的影响.目前为止都只是利用经验法选取合适的参数.但是很显然,对于不同的故障,适用的参数就会不同,因此如何合理地进行参数的选择是本文要研究的重要内容.针对KLPP算法中核函数参数的选择问题,利用集成学习法,本文提出了集成核局部保持投影(ensemble kernel locality preserving projections,EKLPP)算法,并将其用于TE过程进行故障检测.
1 集成核局部保持投影算法 1.1 核局部保持投影算法KLPP[17]算法是LPP算法的非线性延伸[18],KLPP算法首先通过一个非线性映射Φ(·)将原始数据矩阵X =[x1,x2,…,xn]∈Rm×n投影到高维特征空间,然后利用LPP的方法寻找一个投影矩阵A =[a1,a2,…,al],使得高维空间中的数据矩阵Φ (X)=[Φ(x1),Φ(x2),…,Φ(xn)]投影到低维空间Y=[y1,y2,…,yn],即Y = ATΦ (X),使Y尽可能地保留X的邻域结构.
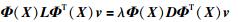
|
(1) |
其中,D为对角阵,其元素为W的列(或行)向量元素和,即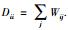

|
(2) |
其中,Wij热核值,t的设定根据经验选择.与KPCA类似,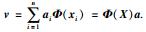
求最佳投影矩阵A,可以转化为求式(3)的广义特征问题的最小特征值所对应的特征向量:
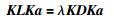
|
(3) |
拉氏矩阵L和对角矩阵D都是对称半正定阵,则KLK和KDK也是对称半正定阵.因此求矩阵(KDK)-1 KLK的特征值对应的最小特征向量,即得到投影矩阵A.
原始数据矩阵经过KLPP投影以后,数据的维数从m维降至l维,可以有效地对数据进行降维,同时矩阵Y保持了原始数据的邻域结构.
1.2 集成核局部保持投影算法传统的KLPP算法只建立单个KLPP模型,通常采用经验法来确定核函数k(x,y)=exp(-(‖x -y‖2/c))中的参数c,即利用c=rnσ2,其中r是常数,n是原始数据矩阵的维数,σ2是原始数据的方差.通常使用的数据在经过标准化之后方差σ2=1,则可简化为c=rn.但对于不同的故障,参数c的选择是不同的,因此这样建立的单个模型并不一定适用于所有故障.为了克服使用单个KLPP模型建模的不足,提出了基于EKLPP建模的方法.不同于单个KLPP建模,EKLPP算法选取了一系列具有不同参数的核函数建立多个子KLPP模型:
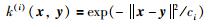
|
(4) |
其中,ci=2i-1rnσ2,i=1,2,…,ns代表核函数的个数.利用这些核函数来建立不同的KLPP模型,可以得到
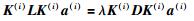
|
(5) |
通过建立的KLPP模型确定每个子KLPP模型的SPE(i)和T2(i),分别计算出两者的控制限SPElimit(i)和Tlimit2(i).
EKLPP模型可以用来检测一个新来的数据集,但是每一个子模型都会得到不同的检测结果,如何将多个子模型的检测结果结合起来是本文要解决的一个重要问题.本文通过贝叶斯决策将所得到的子模型的各统计量的值转化成故障发生的概率,这样就能简化不同子模型的组合问题,便于直接理解故障行为.具体算法为
1) 利用KLPP方法建立多个子模型:
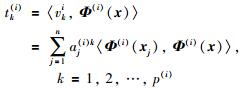
|
(6) |
其中tk(i)为KLPP模型的主元.
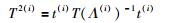
|
(7) |
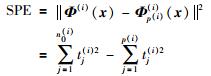
|
(8) |
其中,i=1,2,…,ns,p(i)和n0(i)分别代表第i个子模型的近邻个数和非零特征值个数.
2) 利用贝叶斯决策将两个统计量检测结果转换成故障发生的概率:
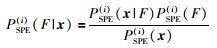
|
(9) |
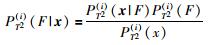
|
(10) |
其中PSPE(i)(x)和PT2(i)(x)通过式(11)和式(12)计算:
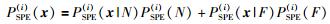
|
(11) |
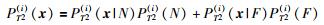
|
(12) |
其中PSPE(i)(N)、PSPE(i)(F)、PT2(i)(N)和PT2(i)(F)分别是第i个子KLPP模型主元空间和残差空间的正常和故障过程的先验概率.如果检验水平α被确定,则PSPE(i)(N)和PT2(i)(N)分别为1-α,PSPE(i)(F)和PT2(i)(F)为α.PSPE(i)(x|N)、PSPE(i)(x|F)、PT2(i)(x|N)和PT2(i)(x|F)计算公式为
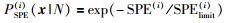
|
(13) |
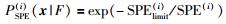
|
(14) |
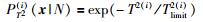
|
(15) |
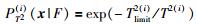
|
(16) |
按上述方法将各子模型的检测结果全部转化为故障发生的概率,再利用式(17)和式(18)将所有的检测结果进行组合:
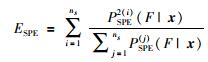
|
(17) |
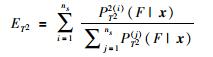
|
(18) |
通常,在生产过程中一旦有一个错误的行为该过程就会被检测成故障,因此本文通常在EKLPP中采用加权的方式进行检测.
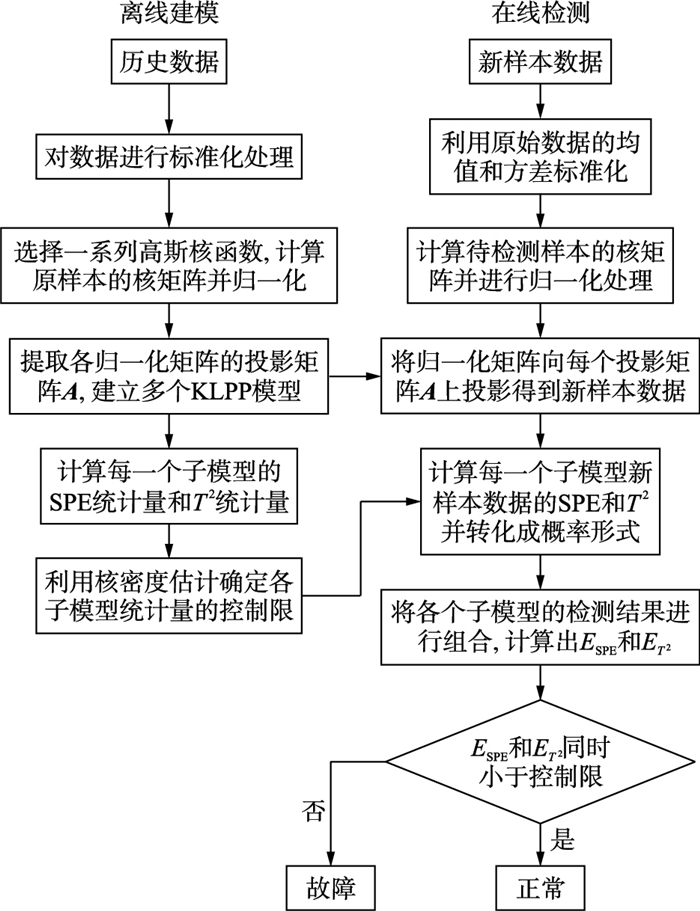
2 基于集成核局部保持投影的故障检测基于EKLPP的故障检测用来判断输入的多个样本数据是否正常,该检测过程分为两步:离线建模和在线仿真.基于集成核局部保持投影的故障检测流程图如图 1所示.
|
| 图 1 基于集成核局部保持投影的故障检测流程图 Figure 1 Flow chart of fault detection based on ensemble kernel locality preserving projection |
离线建模过程为
1) 收集正常操作下的历史数据X=[x1,x2,…,xn]∈ Rm×n,其中m为样本个数,n为变量个数,对数据矩阵X进行标准化处理;
2) 选择一系列具有不同参数的高斯核函数k(i)(x,y)=exp(-(‖x-y‖2/ci)),其中ci=2i-1rnσ2,i=1,2,…,ns代表核函数的个数,r=5[26];
3) 应用每一个高斯核函数对标准化后的X进行核变换,对各核矩阵进行均值中心化,得到训练核向量,即K(i) = K(i)-EK(i)-K(i)E+ EK(i)E[25],其中Eij=1/n(i,j= 1,2,…n),E为与建模数据维数相同的单位阵.
4) 用训练数据求得的每一个K(i)替换原始数据集X,分别在核空间进行LPP投影,得到投影矩阵A (i),建立一系列的子KLPP模型;
5) 计算各子模型的SPE统计量和T2统计量;
6) 利用核密度估计确定各子模型的两个统计量的控制限.
在线检测过程为
1) 新来样本数据Xnew,利用原始数据的均值和方差对新数据矩阵进行标准化处理;
2) 分别利用每一个子KLPP模型对标准化后的数据矩阵进行核函数的转换和中心化,得到待检测的核矩阵K(i)=Kt(i)-EtK(i)-Kt(i)E+EtK(i)E,其中K(i)和E是建模数据的矩阵,Kt(i)=Kt(i)(Xt,X)=Φ(Xt)Φ(X),X是训练数据,Xt是待检测数据,Etij=1/n(i,j=1,2,…,n).
3) 用核矩阵K(i)代替新来样本数据Xnew,并利用矩阵A(i)将其投影到每一个子KLPP模型上,得到新的样本数据;
4) 分别计算每一个子模型新样本数据的SPE和T2;
5) 计算每一个子模型两个统计量发生故障的概率;
6) 将各个子模型的检测结果进行组合,计算出ESPE和ET2;
7) 将待检测样本的ESPE和ET2与控制限α进行比较,根据统计量是否超过控制限来判断是否发生故障.
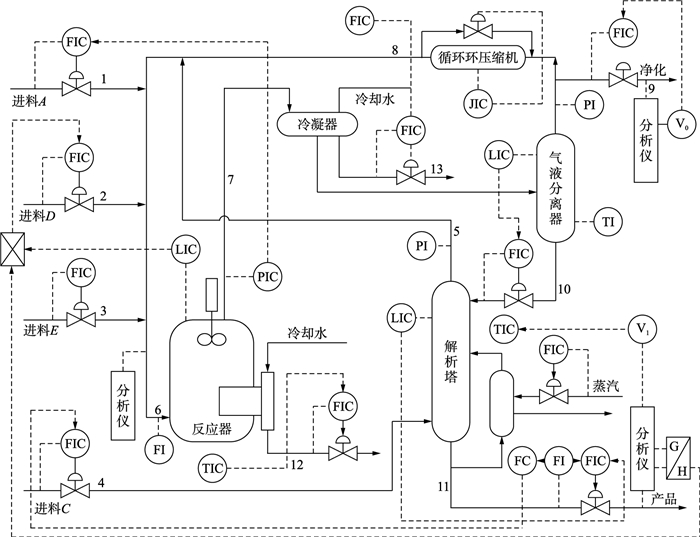
3 仿真结果与分析 3.1 TE过程Eastman化学公司开发的Tennessee Esatman(田纳西—伊斯曼过程)过程模拟器提供了一个实际的工业过程仿真平台,近年来已经被广泛用于验证各种故障检测与诊断方法,现已成为一种国际上通用的标准仿真模型[19-22].这个过程模型首先是以FORTRAN源代码的形式提供给过程控制学界,主要描述了装置、物料和能量之间的非线性关系.TE过程包括5个主要操作单元、4种气体进料、2个气液放热反应生成的2种主产品、2个衍生放热反应生成的2种副产品等,过程机理复杂性极高,变量较多.具体模型流程图如图 2所示.
|
| 图 2 TE过程工艺流程图 Figure 2 Flow chart of TE process |
将集成核局部保持投影应用到TE过程中,并与PCA[23] (principal component analysis)、LPP(locality preserving projection)[18]、OLPP(orthogonal LPP)[24]、KPCA(kernel PCA)[25-26]、KLPP(kernel LPP)[27]、KOLPP(kernal based OLPP)[28]和EKPCA(ensemble KLPP)[29]算法进行比较.8种算法的主元或潜变量的个数均为30个,EKLPP的子模型个数为11.以第400个采样时刻为例,11个子模型及集成模型的两个统计量SPE和T2的取值对比如表 1所示.表 1中集成模型的SPE和T2的值是由11个子模型的值组合得到的.文中KPCA、KLPP和KOLPP的核参数均为8 320.本文选取TE数据的故障2、5、6、18来验证算法的有效性.
| 模型 | 故障2 | 故障5 | 故障6 | 故障18 | ||||
| SPE /10-4 | T2/10-4 | SPE /10-4 | T2/10-4 | SPE /10-4 | T2/10-4 | SPE /10-4 | T2/10-4 | |
| 1 | 6 048 | 8.193 | 6 048 | 8.193 | 6 048 | 8.193 | 19 400 | 38 |
| 2 | 2 313 | 3.550 | 2 313 | 3.542 | 2 313 | 3.542 | 8 295 | 7.888 |
| 3 | 736 | 4.203 | 717 | 4.248 | 717 | 4.248 | 2 722 | 1.460 |
| 4 | 593 | 4.824 | 200 | 4.803 | 200 | 4.829 | 781 | 0.192 |
| 5 | 927 | 156 | 57 | 362 | 47 | 340 | 209 | 0.234 |
| 6 | 215 | 2 312 | 13 | 20 | 80 | 227 | 17 | 90 |
| 7 | 88 | 987 | 33 | 175 | 217 | 626 | 4.393 | 23 |
| 8 | 30 | 341 | 44 | 442 | 125 | 549 | 1.126 | 6.332 |
| 9 | 8.664 | 98 | 34 | 338 | 56 | 245 | 0.284 | 1.592 |
| 10 | 2.313 | 26 | 15 | 147 | 19 | 82 | 0.071 1 | 0.399 |
| 11 | 6.020 | 6.732 9 | 4.195 | 49 | 5.423 | 24 | 0.017 7 | 0.010 |
| 集成 | 9 807 | 9 893 | 9 442 | 9 487 | 9 796 | 9 840 | 59 | 70 |
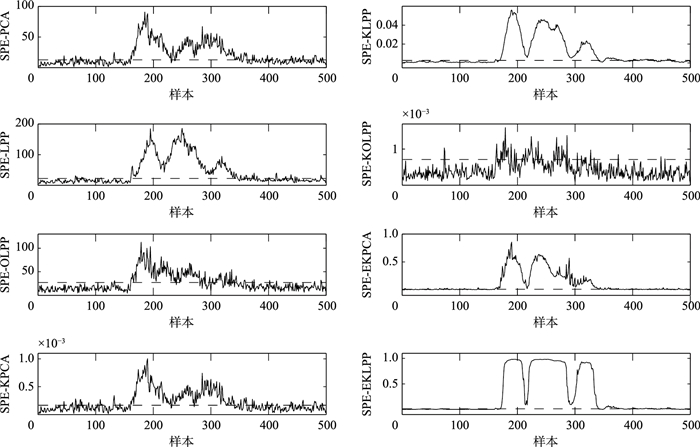
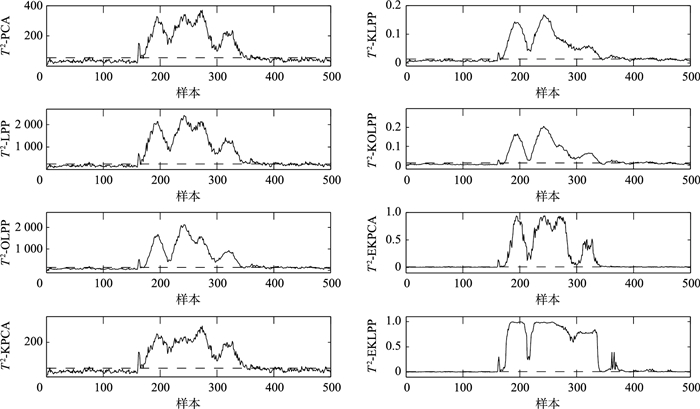
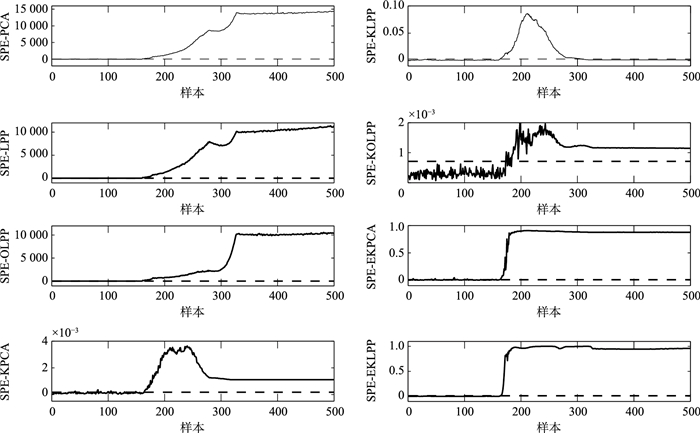
故障5和故障6的SPE和T2统计量的检测结果分别如图 3~图 6所示.图中虚线为两个统计量99%的控制限.TE数据的故障均从第161时刻开始引入,从图 3和图 4可以看出PCA算法、LPP算法、KPCA算法、KOLPP算法和EKPCA算法都有误报产生,而EKLPP算法误报并不明显.而且OLPP算法和KOLPP算法T2的漏报明显.主要是由于本文的算法既有效地提取数据的非线性局部特征,又解决不同故障核参数的选择问题.从图 5和图 6可以看出KPCA算法和EKPCA算法在161时刻之前产生误报,EKLPP算法的误报较低;KPCA、KLPP和KOLPP算法在故障发生后的大部分时刻统计量都低于控制限,漏报情况明显,而EKLPP算法明显能检测出全部故障.综上,与其它7种算法相比,EKLPP算法在前160个时刻基本没有超过控制限的情况,错误率最低,故障检测效果最好,由此证明了该算法的有效性.EKLPP算法既解决了非线性数据的检测问题,同时也弥补了传统KLPP算法核参数选择的不足,通过贝叶斯决策将具有不同核参数的子模型进行组合,使组合后的集成模型可以适用于检测不同类型的故障.
|
| 图 3 故障5的SPE检测结果 Figure 3 SPE detection results of fault 5 |
|
| 图 4 故障5的T2检测结果 Figure 4 T2 detection results of fault 5 |
|
| 图 5 故障6的SPE检测结果 Figure 5 SPE detection results of fault 6 |
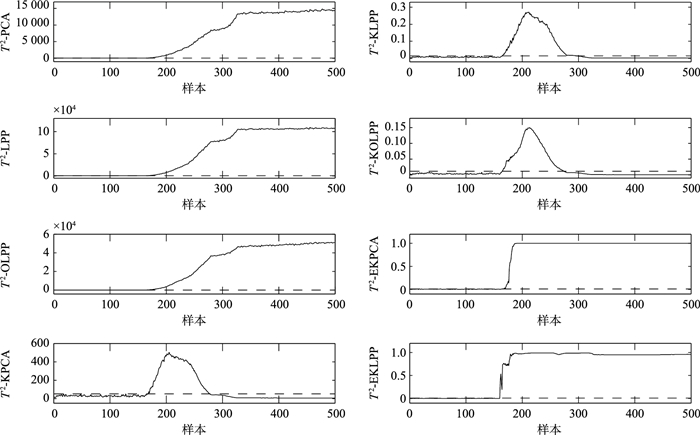
|
| 图 6 故障6的T2检测结果 Figure 6 T2 detection results of fault 6 |
8种算法的具体检测结果如表 2所示.本文运用误报率、漏报率及两个指标的和(错误率)来衡量算法的好坏,由表 2可以看出,在对4个故障(2、5、6、18)进行检测的情况下,与PCA、LPP、OLPP、KPCA、KLPP、KOLPP和EKPCA算法相比,EKLPP的SPE统计量和T2统计量的错误率指标均最低,因此该算法的故障检测效果最好,验证了该算法的有效性.
| 故障 | 算法 | SPE | T2 | ||||
| 误报率/(%) | 漏报率/(%) | 错误率/(%) | 误报率/(%) | 漏报率/(%) | 错误率/(%) | ||
| 2 | PCA | 11.25 | 0.75 | 12 | 1.25 | 1.62 | 2.87 |
| LPP | 6.88 | 1.5 | 8.38 | 1.25 | 1.25 | 2.5 | |
| OLPP | 2.5 | 1.62 | 4.12 | 0.63 | 1.38 | 2.01 | |
| KPCA | 13.13 | 0.87 | 14 | 2.5 | 1.37 | 3.87 | |
| KLPP | 0 | 1.75 | 1.75 | 0 | 1.25 | 1.25 | |
| KOLPP | 1.25 | 2.75 | 4 | 0 | 1.75 | 1.75 | |
| EKPCA | 15 | 1 | 16 | 3.13 | 1.75 | 4.88 | |
| EKLPP | 0 | 1.75 | 1.75 | 0 | 1.25 | 1.25 | |
| 5 | PCA | 14.37 | 56.37 | 70.74 | 0.63 | 72.5 | 73.13 |
| LPP | 6.88 | 67.62 | 74.5 | 3.13 | 64.62 | 67.75 | |
| OLPP | 2.5 | 76.5 | 79 | 1.25 | 64.5 | 65.75 | |
| KPCA | 18.13 | 62.5 | 80.63 | 3.13 | 69.75 | 72.88 | |
| KLPP | 0.63 | 64.75 | 65.38 | 3.13 | 64.87 | 68 | |
| KOLPP | 1.25 | 91.25 | 92.5 | 0.63 | 67 | 67.63 | |
| EKPCA | 21.88 | 61.62 | 83.5 | 2.5 | 68 | 70.5 | |
| EKLPP | 1.25 | 64 | 65.25 | 1.25 | 62.25 | 63.5 | |
| 6 | PCA | 6.88 | 0 | 6.88 | 0 | 0.87 | 0.87 |
| LPP | 1.25 | 0 | 1.25 | 1.25 | 0.37 | 1.62 | |
| OLPP | 2.5 | 0 | 2.5 | 0 | 0.5 | 0.5 | |
| KPCA | 11.25 | 0.37 | 11.62 | 1.88 | 86.25 | 88.13 | |
| KLPP | 0 | 82.12 | 82.12 | 0 | 83.25 | 83.25 | |
| KOLPP | 0 | 2 | 2 | 0 | 86.5 | 86.5 | |
| EKPCA | 10.63 | 0.25 | 10.88 | 0 | 0.62 | 0.62 | |
| EKLPP | 0 | 0.37 | 0.37 | 0 | 0 | 0 | |
| 18 | PCA | 15.63 | 7.87 | 23.5 | 0.63 | 10.62 | 11.25 |
| LPP | 3.13 | 9 | 12.13 | 4.38 | 9.5 | 13.88 | |
| OLPP | 1.88 | 10 | 11.88 | 1.25 | 9.62 | 10.87 | |
| KPCA | 17.5 | 7.13 | 24.63 | 1.88 | 81.38 | 83.26 | |
| KLPP | 0 | 75.37 | 75.37 | 2.5 | 75.87 | 78.37 | |
| KOLPP | 1.88 | 12.12 | 14 | 0 | 76.88 | 76.88 | |
| EKPCA | 19.38 | 7.62 | 27 | 3.13 | 9.62 | 12.75 | |
| EKLPP | 0 | 8.75 | 8.75 | 1.25 | 8.25 | 9.5 | |
本文提出一种基于集成核局部保持投影的连续过程故障诊断算法.选取一系列具有不同参数的高斯核函数构造核矩阵来代替原始数据矩阵,将原始数据投影到高维空间,在有效提取数据非线性信息的同时保留了原始数据的局部结构.利用贝叶斯决策将检测结果转换成发生故障的概率形式,再通过集成学习法将各个模型的检测结果结合进行检测.EKLPP算法有效地克服了传统KLPP算法对于不同故障的核参数选择问题.将本文的方用到实际的TE数据中,通过仿真结果表明,与传统的故障检测算法相比,本文提出的算法错误率最低,验证了该方法的优越性.
虽然本文提出的算法具有明显的优势,但检测结果会受到所选子模型数量的影响.如何选择合适数量的子模型使检测效果达到最佳是本文要进一步研究的内容.
| [1] |
周东华, 李钢, 李元.
数据驱动的工业过程故障检测与诊断技术[M]. 北京: 科学出版社, 2011: 1-76.
Zhou D H, Li G, Li Y. Fault detection and diagnosis technology of industrial process based on data driven[M]. Beijing: Science Press, 2011: 1-76. |
| [2] |
郭金玉, 齐蕾蕾, 李元.
基于DMOLPP的间歇过程在线故障检测[J]. 仪器仪表学报, 2015, 36(1): 28–36.
Guo J Y, Qi L L, Li Y. On-line fault detection of batch process based on DMOLPP[J]. Chinese Journal of Scientific Instrument, 2015, 36(1): 28–36. |
| [3] |
谢彦红, 孙呈敖, 李元.
基于滑动窗口SVDD的间歇过程故障监测[J]. 信息与控制, 2015, 44(5): 531–537.
Xie Y H, Sun C A, Li Y. Fault monitoring of batch process based on moving window SVDD[J]. Information and Control, 2015, 44(5): 531–537. |
| [4] |
郭金玉, 陈海彬, 李元.
基于在线升级主样本建模的批次过程kNN故障检测方法[J]. 信息与控制, 2014, 43(4): 495–500.
Guo J Y, Chen H B, Li Y. kNN fault detection method for batch process based on principal sample modeling upgraded online[J]. Information and Control, 2014, 43(4): 495–500. |
| [5] |
王亚君, 周岐.
基于多动态核PCA的统计过程监测策略研究[J]. 辽宁工业大学学报:自然科学版, 2012, 32(5): 295–298.
Wang Y J, Zhou Q. Research on statistical process monitoring strategy based on multi-dynamic kernel PCA[J]. Journal of Liaoning University of Technology:Natural Science Edition, 2012, 32(5): 295–298. |
| [6] |
许洁, 胡寿松, 申忠宇.
基于改进多尺度核主元分析的化工过程故障检测与诊断方法研究[J]. 仪器仪表学报, 2010, 31(1): 51–55.
Xu J, Hu S S, Shen Z Y. Fault detection and diagnosis of chemical process based on an improved multi-scale KPCA[J]. Chinese Journal of Scientific Instrument, 2010, 31(1): 51–55. |
| [7] | ZhaoXQ, WangXM, Wu Y. An improved FVS-KPCA method of fault detection on TE process[C]//Third International Conference on Digital Manufacturing and Automation. Piscataway, NJ, USA: IEEE, 2012: 186-189. |
| [8] |
魏秀业, 潘宏侠, 王福杰.
基于粒子群优化的核主元分析特征的提取技术[J]. 振动、测试与诊断, 2009, 29(2): 162–166, 240.
Wei X Y, Pan H X, Wang F J. Feature extraction based on kernel principal component analysis optimized by particle swarm optimization algorithm[J]. Journal of Vibration, Measurement & Diagnosis, 2009, 29(2): 162–166, 240. |
| [9] | Xiao Y W, Zhang X H. Novel nonlinear process monitoring and fault diagnosis method based on KPCA-ICA and MSVMs[J]. Journal of Control, Automation and Electrical Systems, 2016, 27(3): 289–299. DOI:10.1007/s40313-016-0232-8 |
| [10] | Joshph A A, Tokumoto T, Ozawa S. Online feature extraction based on accelerated kernel principal component analysis for data stream[J]. Evolving Systems, 2016, 7(1): 15–27. DOI:10.1007/s12530-015-9131-7 |
| [11] | He X, Cai D, Yan S, et al. Neighborhood preserving embedding[C]//Proceedings of the Tenth IEEE International Conference on Computer Vision. Piscataway, NJ, USA: IEEE, 2005: 1208-1213. |
| [12] | Hu K, Yuan J. Multivariate statistical process control based on multiway locality preserving projections[J]. Journal of Process Control, 2008, 18(7): 797–807. |
| [13] | Cai D, He X, Han J, et al. OrthogonalLaplacianfaces for face recognition[J]. IEEE Transactions on Image Processing, 2006, 15(11): 3608–3614. DOI:10.1109/TIP.2006.881945 |
| [14] | He F, Xu J W. A novel process monitoring and fault detection approach based on statistics locality preserving projections[J]. Journal of Process Control, 2016, 37(5): 46–57. |
| [15] | Jiang R, Fu W J, Wen L, et al. Dimensionality reduction on Anchorgraph with an efficient locality preserving projection[J]. Journal of Process Control, 2016, 187: 109–118. |
| [16] | Cai D, He X, Han J, et al. Orthogonal laplacianfaces for face recognition[J]. IEEE Transactions on Image Processing, 2006, 15(11): 3608–3614. DOI:10.1109/TIP.2006.881945 |
| [17] | Luo L J, Bao S Y, Mao J F, et al. Nonlinear process monitoring based on kernel global-local preserving projections[J]. Journal of Process Control, 2016, 38: 11–21. DOI:10.1016/j.jprocont.2015.12.005 |
| [18] | He X, Niyogi P. Locality preserving projections[J]. Advances in Neural Information Processing Systems, 2005, 45(1): 186–197. |
| [19] | Downs J J, Vogel E F. A plant-wide industrial process control problem[J]. Computers and Chemical Engineering, 1993, 17(3): 245–255. DOI:10.1016/0098-1354(93)80018-I |
| [20] | Mcavoy T J, Ye N. Base control for the Tennessee Eastman problem[J]. Computers & Chemical Engineering, 1994, 18(5): 383–413. |
| [21] | Lee G, Han C, Yoon E S. Multiple-fault diagnosis of the Tennessee Eastman process based on system decomposition and dynamic PLS[J]. Industrial & Engineering Chemistry Research, 2004, 43(25): 8037–8048. |
| [22] | Yin S, Ding S X, Haghani A, et al. A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process[J]. Journal of Process Control, 2012, 22(9): 1567–1581. DOI:10.1016/j.jprocont.2012.06.009 |
| [23] | Villegas T, Fuente M J, Rodríguez M. Principal component analysis for fault detection and diagnosis. experience with a pilot plant[C]//Proceedings of the 9th WSEAS International Conference on Computational Intelligence, Man-machine Systems and Cybernetics. Piscataway, NJ, USA: IEEE, 2010. |
| [24] | Sun B, Liu L, Lei W. Rotor fault diagnosis method based on orthogonal locality preserving projection[J]. China Mechanical Engineering, 2014, 25(16): 2219–2224. |
| [25] | Schölkopf B, Smola A, Müller K R. Kernel principal component analysis[M]. Cambridge, MA, USA: MIT Press, 1997: 555-559. |
| [26] | Cho J H, Lee J M, Sang W C, et al. Fault identification for process monitoring using kernel principal component analysis[J]. Chemical Engineering Science, 2005, 60(1): 279–288. DOI:10.1016/j.ces.2004.08.007 |
| [27] | Cheng J, Liu Q, Lu H, et al. Supervised kernel locality preserving projections for face recognition[J]. Neurocomputing, 2005, 67(1): 443–449. |
| [28] | Jin Y. Kernel based orthogonal locality preserving projections for face recognition[J]. Journal of Electronics & Information Technology, 2009, 31(2): 283–287. |
| [29] | Li N, Yang Y. Ensemble kernel principal component analysis for improved nonlinear process monitoring[J]. Industrial & Engineering Chemistry Research, 2015, 54(1): 318–329. |



