0 引言
随着现代工业的飞速发展,尤其是信息技术广泛而深入的应用,工业系统正朝着大规模化、高度复杂化、自动化、智能化的方向快速发展,因此系统发生故障并引起事故的可能性也随之大大增加,所以对控制精度和可靠性的要求也越来越高,人们迫切需要建立一个具有高性能的监控系统来监视系统的运行状态,实时检测出系统发生的故障.因此基于数据驱动的故障检测技术在工业过程中得到了广泛应用.其中基于多元统计分析的故障诊断方法已成功应用于工业过程检测与监视,并成为工业界和学术界的研究热点[1].
多元统计分析中,主元分析(principal component analysis,PCA)[2]和偏最小二乘(partial least squares,PLS)[3]及其拓展算法受到了广泛的关注[4-7].但是PCA是线性算法,无法提取数据的非线性结构特征,因此研究人员提出非线性方法[8-9].核主元分析KPCA(kernel principal component analysis)[10]是一种非线性方法,是Scholkopft等在研究支持矢量类算法时提出的.然而传统的KPCA算法对非线性过程检测效果并不是很好,原因是KPCA保留数据样本的全局信息,造成局部信息的丢失.在故障检测问题中,局部结构比全局结构更重要.因此,寻找保留原始数据局部结构的方法开始得到学术界的关注[11].Hu等[12]提出了局部保持投影算法(locality preserving projections,LPP),保留了数据的局部信息,更好地对其进行检测.Luo等[13]将局部算法应用于非线性生产过程,提出了核局部保持投影(kernel locality preserving projections,KLPP)算法,提高了检测效果.但KLPP方法的检测效果受到核参数的影响.目前为止,如何选取合适的参数仍是一个难题.LPP是一种线性方法,对非线性过程检测效果不够理想.为了解决这个问题,本文尝试将差分算法和LPP算法相结合,提出一种新的基于差分局部保持投影(differencial locality preserving projections,DLPP)的非线性工业过程故障检测方法.差分算法是一种线性化方法,可以剔除数据的(拉谱拉斯特征谱),为局部保持投影算法提供所需要的数据特点,与此同时提高非线性过程的故障检测性能.
1 局部保持投影算法LPP算法[14-16]是一种用于提取数据特征信息的降维方法.它可以很好地保留数据的局部信息,主要考虑的是保持数据中近邻点之间的结构,其本质是对拉普拉斯特征映射的线性逼近.它是LE剔除数据的(拉普拉斯特征谱)算法的扩展,且与LE的目标函数相同,但是它使用显式的线性映射.算法的核心是寻找转换矩阵A使一系列的X =[x1 x2 … xn]∈Rm×n投影到Y =[y1 y2 … yn]∈Rl×n(l << m)上,即yi=ATxi,使Y尽可能地代表X.求解A可以通过优化式(1)的最小值问题:
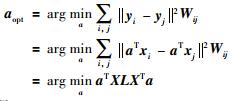
|
(1) |
约束条件是:
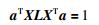
|
(2) |
式中,L是拉普拉斯矩阵,L=D-W,W是定义在数据点上的相似矩阵,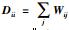
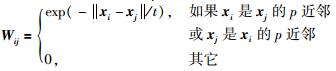
|
(3) |
其中Wij是加权矩阵,t的设定根据经验选择.求目标函数的最小值可以保证近邻点xi和xj的投影yi和yj也是近邻点.寻求最佳投影矩阵A转化为求下式广义特征问题的最小特征值所对应的特征向量:
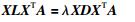
|
(4) |
其中XLXT和XDXT都是对称且半正定的,因此求矩阵(XDXT)-1XLXT的最小特征值对应的特征向量,即得到投影矩阵A.
2 基于差分LPP的非线性过程故障检测 2.1 差分算法差分算法能够在保持数据内部结构的条件下,剔除数据的非线性结构.对数据矩阵X(m×n)(m代表采样次数,n代表测量变量个数)中第i个样本Xi,n,找到该样本的最近邻Xk,n,然后进行差分运算,计算方式为
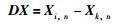
|
(5) |
其中,DX(m×n)是差分矩阵.
本节通过一个人工合成的非线性数值例子[17]比较差分之前和差分之后的结果,验证差分算法可以剔除数据的非线性结构的有效性.数值仿真过程由两个变量组成,具体数据来源于式(6):
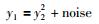
|
(6) |
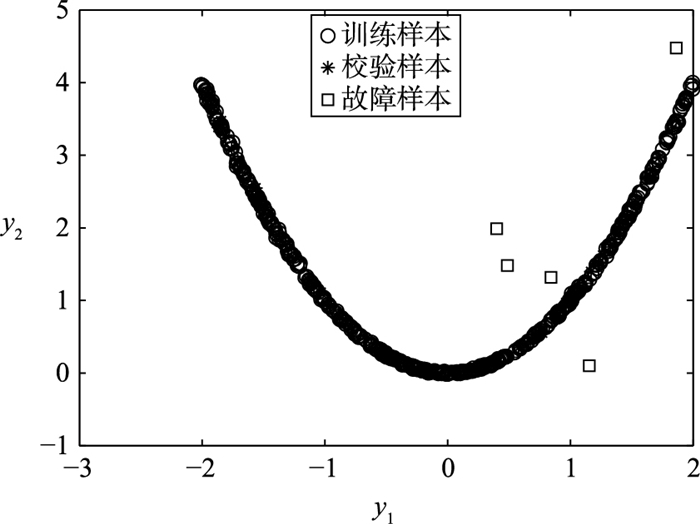
生成500个正常数据用作训练样本,100个正常数据用作校验样本,5个异常数据用作故障样本.图 1是训练样本、校验样本、故障样本的数据分布散点图.
|
| 图 1 数据分布散点图 Figure 1 The scatter plot of data distribution |
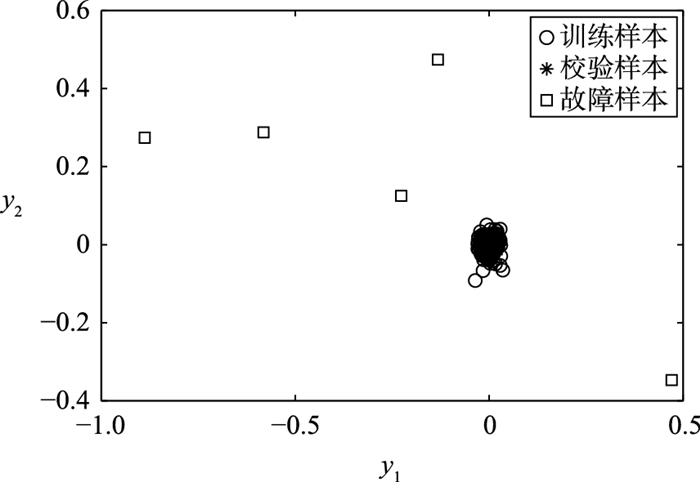
由此可见,本文所用到的数值例子是非线性的.对训练样本、校验样本、故障样本分别进行差分运算后得到的数据分布散点图如图 2所示.
|
| 图 2 差分后的数据分布散点图 Figure 2 The scatter plot of data distribution after differencial algorithm |
通过图 1和图 2的比较可以很直观地看出差分算法可以剔除数据的非线性结构,从而验证了该算法的有效性.
在同一模态内,每个样本和其最近邻的区别较小,因此差分能够剔除数据的相似性.同一模态内的样本,其差分矩阵主要是噪声,近似服从正态分布,所以该算法能够剔除数据的非线性结构.
2.2 基于差分局部保持投影算法由于LPP算法是线性算法,无法处理非线性问题,而差分算法能够剔除数据的非线性结构,所以本文将差分算法和局部保持投影算法相结合提出了基于差分局部保持投影的算法.
用LPP算法对上述所提到的数值例子进行处理,得到如图 3所示的主元图.

|
| 图 3 LPP算法处理后的数值例子主元图 Figure 3 The principal component plot of the value example after LPP algorithm |
上述所提到的数值例子是非线性的,由图 3的主元图可以看出:经过LPP算法处理后的数值例子仍然是非线性的.所以验证了LPP算法是线性算法,无法去掉非线性.因此本文将差分算法和LPP算法相结合,利用差分方法,剔除数据的非线性结构,并利用LPP方法确定SPE统计量,保持了数据的局部结构,能够更好地处理非线性问题.
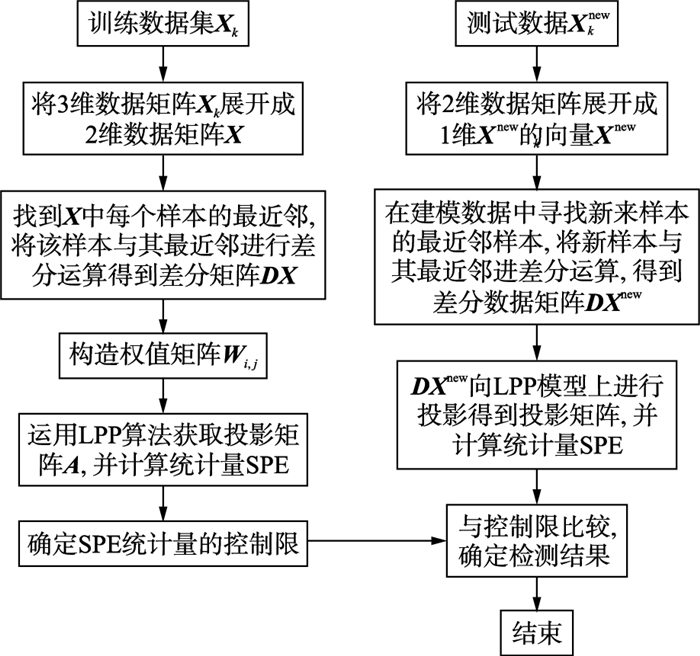
2.3 基于差分LPP的非线性过程故障检测基于差分LPP的非线性过程故障检测包括建立模型和故障检测两个部分.该算法的整体流程图如图 4所示.具体步骤为
|
| 图 4 基于差分局部保持投影的非线性过程故障检测流程图 Figure 4 Flow chart of fault detection for nolinear process based on differencial locality preserving projections |
1) 建立正常状态下的模型
(1) 收集正常操作时的间歇过程历史数据Xk(I×J×d),其中I是批次数,J是变量数,d是一个批次过程总的反应时刻数.
(2) 将数据矩阵Xk(I×J×d)沿批次方向展开成2维数据矩阵X(I×Jd);
(3) 对数据集X(I×Jd)中的每个样本,找到其最近邻,将该样本与其最近邻进行差分运算得到差分矩阵DX;
(4) 利用式(3)构造权值矩阵Wi,j;
(5) 选择合适的参数,运用LPP算法获取投影矩阵A,并计算统计量SPE,建立正常工况下的LPP模型.
(6) 利用核密度估计的方法确定统计量SPE的95%控制限.
2) 故障检测
(1) 新来一个时刻k的批次数据,将数据Xknew(J×d)展开成Xnew(1×dJ);
(2) 在建模数据中寻找新来样本的最近邻样本,将新样本与其最近邻样本进行差分运算,得到差分数据矩阵Xnew;
(3) 新样本的差分矩阵向LPP模型上进行投影得到投影矩阵,并计算统计量SPE;
(4) 通过比较Xnew的SPE是否超过控制限来判断当前过程是否正常,如果Xnew超出控制限则为故障样本,否则Xnew为正常样本.
3 仿真结果与分析本文给出两个例子分别验证基于DLPP的非线性过程故障检测方法的有效性.第1个例子是具有非线性特性的数值例子;第2个例子是半导体间歇过程数据.
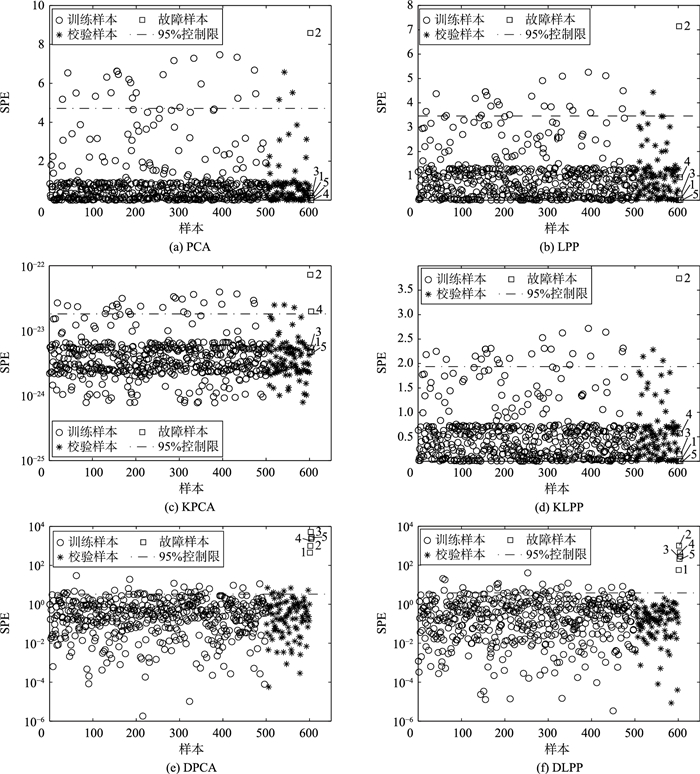
3.1 数值例子在对2.1节提到的数值例子,分别使用PCA、LPP、KPCA、KLPP、DPCA和DLPP方法进行故障检测.当KPCA和KLPP的核参数取3 000 000时,取6种方法最优的故障检测结果,如图 5所示.图中的虚线是SPE统计量95%的控制限.
|
| 图 5 6种算法对数值例子的检测结果 Figure 5 The detection results of six algorithms for the value example |
由图 5可知,运用PCA算法进行故障检测时,有3个校验数据没有检测出来,而故障数据有4个没有检测出来.运用LPP算法时,校验数据有2个没有检测出来,故障数据有4个没有检测出来.运用KPCA算法时,校验数据和故障数据均有3个没有检测出来.运用KLPP算法时,校验数据有3个没有检测出来,故障数据有1个没有检测出来.运用DPCA算法时,校验数据有7个没有检测出来,而故障数据全部检测出来.运用DLPP算法进行检测时,校验数据和故障数据全部检测出来.由此可见,DLPP算法的检测效果最好.
6种算法对数值例子的具体检测结果如表 1所示.运用95%控制限下的误报率、漏报率来衡量算法的好坏.由表 1可以看出,与其它5种算法相比,DLPP算法检测效果最好,误报率和漏报率均为0,验证了DLPP在非线性过程故障检测方面的优势.
| 算法 | 误报率/(%) | 漏报率/(%) |
| PCA | 3 | 80 |
| LPP | 2 | 80 |
| KPCA | 3 | 60 |
| KLPP | 3 | 80 |
| DPCA | 7 | 0 |
| DLPP | 0 | 0 |
本文所应用的半导体数据来源于美国德州仪器公司的半导体生产过程实际数据.该数据是由3个阶段的108个正常批次和21个故障批次组成.第1阶段有34个批次的正常样本和9个批次的故障样本;第2阶段有37个批次的正常样本和6个故障样本;第3阶段有37个批次的正常样本和6个故障样本.由于第2阶段的1个正常批次和1个故障批次大量缺失数据,只有107个正常批次和20个故障批次是有效的.本文选取17个过程变量用于故障检测方法对比的仿真实验[18-21].每个模态分别选取32个批次用于建模,剩下的正常批次作为校验批次用来验证模型的准确性,因此建模批次为96个,正常校验为11个,故障批次为20个.
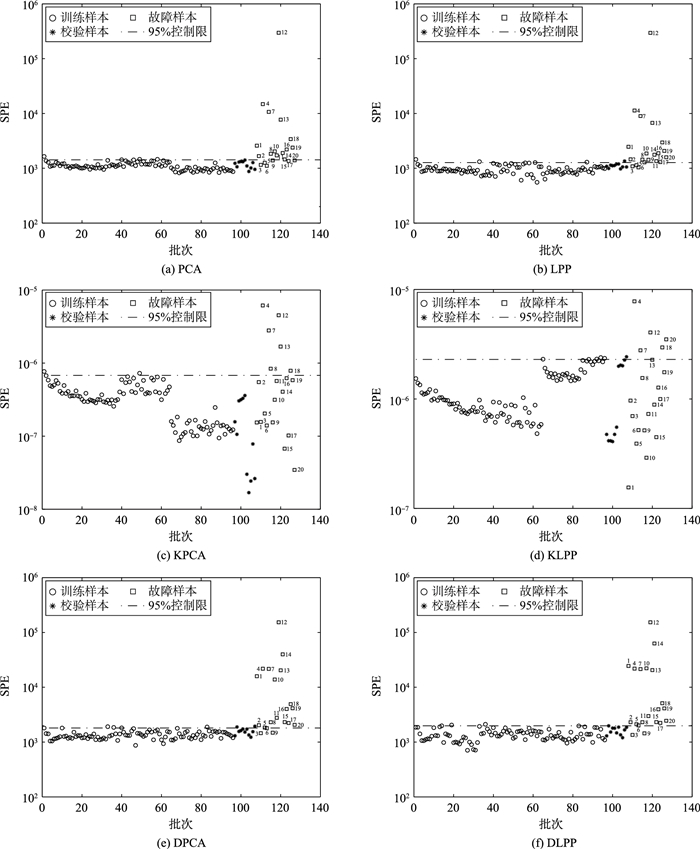
当KPCA和KLPP算法的核参数取3 000 000时,取六种算法的最优检测效果进行对比分析.图 6是这六种方法应用于半导体过程数据的故障检测结果.图中的虚线是SPE统计量的95%控制限.由图 6可以看出,运用PCA算法进行故障检测时,校验数据全部检测出来,而故障数据有6个没有检测出来.运用LPP算法时,校验数据有1个没有检测出来,故障数据有3个没有检测出来.运用KPCA算法进行检测时,校验数据全部检测出来,故障数据有14个没有检测出来.运用KLPP算法进行检测时,校验数据有1个没有检测出来,故障数据有15个没有检测出来.运用DPCA算法时,校验数据有2个没有检测出来,故障数据有3个没有检测出来.运用DLPP算法进行检测时,校验数据全部检测出来,故障数据有2个没有检测出来.由此可见,LPP算法的故障检测性能要优于PCA算法的检测性能,这是由于PCA算法提取的是数据的全局特征,而LPP算法提取数据的局部特征.与PCA、LPP、KPCA、KLPP和DPCA算法相比,DLPP算法的检测效果最佳.
|
| 图 6 6种算法对半导体过程数据的检测结果 Figure 6 The detection results of six algorithms for the semiconductor process data |
表 2是6种算法对半导体过程数据的具体检测结果统计.由表 2可以看出,对非线性过程故障进行检测,6种算法中,DLPP算法的误报率和漏报率最低.与其它5种算法相比,DLPP的故障检测效果最好,验证了该算法的有效性.
| 算法 | 误报率/(%) | 漏报率/(%) |
| PCA | 0 | 30 |
| LPP | 9 | 15 |
| KPCA | 0 | 70 |
| KLPP | 9 | 75 |
| DPCA | 18 | 15 |
| DLPP | 0 | 10 |
本文提出一种基于差分局部保持投影的非线性过程故障检测方法.利用差分方法,剔除数据的非线性结构并利用LPP方法确定SPE统计量,进行故障检测.最后,将差分局部保持投影算法应用于工业过程统计监视.数值例子和半导体过程数据的仿真结果表明,差分局部保持投影算法与其余五种算法相比,检测效果最佳.
| [1] |
周东华, 李钢, 李元.
数据驱动的工业过程故障检测与诊断技术[M]. 北京: 科学出版社, 2011: 1-76.
Zhou D H, Li G, Li Y. Fault detection and diagnosis technology of industrial process based on data driven[M]. Beijing: Science Press, 2011: 1-76. |
| [2] | Wold S, Esbensen K, Geladi P. Principal component analysis[J]. Chemometrics and Intelligent Laboratory Systems, 1987, 2(1/2/3): 37–52. |
| [3] | Nomikos P, Macgregor J F. Multi-way partial least squares in monitoring batch processes[J]. Chemometrics and Intelligent Laboratory Systems, 1995, 30(1): 97–108. DOI:10.1016/0169-7439(95)00043-7 |
| [4] | Li Y, Zhang X. Diffusion maps based k-nearest-neighbor rule technique for semiconductor manufacturing process fault detection[J]. Chemometrics and Intelligent Laboratory Systems, 2014, 136(15): 47–57. |
| [5] |
郭小萍, 李婷, 李元.
基于鲁棒测地线距离的复杂间歇过程故障检测[J]. 仪器仪表学报, 2014, 35(12): 2681–2689.
Guo X P, Li T, Li Y. Complex batch process fault detection based on robust geodesic distance[J]. Chinese Journal of Scientific Instrument, 2014, 35(12): 2681–2689. |
| [6] |
谢彦红, 孙呈敖, 李元.
基于滑动窗口SVDD的间歇过程故障监测[J]. 信息与控制, 2015, 44(5): 531–537.
Xie Y H, Sun C A, Li Y. Fault monitoring of batch process based on sliding window SVDD[J]. Information and Control, 2015, 44(5): 531–537. |
| [7] |
张成, 李元, 高宪文.
基于稀疏距离的间歇过程故障检测方法[J]. 信息与控制, 2014, 43(5): 588–595.
Zhang C, Li Y, Gao X W. Fault detection method based on sparse distance in batch process[J]. Information and Control, 2014, 43(5): 588–595. |
| [8] |
张汉元, 田学民.
基于KSFDA-SVDD的非线性过程故障检测方法[J]. 化工学报, 2016, 67(3): 827–832.
Zhang H Y, Tian X M. Nonlinear process fault detection method based on KSFDA-SVDD[J]. Journal of Chemical Industry, 2016, 67(3): 827–832. |
| [9] |
唐勇波, 桂卫华, 欧阳伟.
基于KPCA和CPSO的故障检测方法[J]. 计算机工程, 2012, 38(24): 244–246, 250.
Tang Y B, Gui W H, Ouyang W. Fault detection method based on KPCA and CPSO[J]. Computer Engineering, 2012, 38(24): 244–246, 250. DOI:10.3969/j.issn.1000-3428.2012.24.057 |
| [10] | Schölkopf B, Smola A, Müller K R. Nonlinear component analysis as a kernel eigenvalue problem[J]. Neural Computation, 1998, 10(5): 1299–1319. DOI:10.1162/089976698300017467 |
| [11] | He X F, Yan S C, Hu Y X, et al. Face recognition using Laplacian faces[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(3): 328–340. DOI:10.1109/TPAMI.2005.55 |
| [12] | Hu K, Yuan J. Multivariate statistical process control based on multiway locality preserving projections[J]. Journal of Process Control, 2008, 18(7): 797–807. |
| [13] | Luo L J, Bao S H Y, Mao J F, et al. Nonlinear process monitoring based on kernel global-local preserving projections[J]. Journal of Process Control, 2016, 38: 11–21. DOI:10.1016/j.jprocont.2015.12.005 |
| [14] | Belkin M, Niyogi P. Laplacian eigenmaps and spectral techniques for embedding and clustering[C]//Advances in Neural Information Processing Systems. Berlin, Germany: Springer, 2001, 14: 585-591. |
| [15] | Dornaika F, Assoum A. Enhanced and parameterless locality preserving projections for face recognition[J]. Neurocomputing, 2013, 99(1): 448–457. |
| [16] | Heng Z, Liu J J, WU C X, et al. A new construction method of neighbor graph for locality preserving projections[J]. Journal of Information and Computational Science, 2013, 10(5): 1357–1365. DOI:10.12733/issn.1548-7741 |
| [17] | He Q P, Wang J. Fault Detection using the k-nearest neighbor rule for semiconductor manufacturing processes[J]. IEEE Transactions on Semiconductor Manufacturing, 2007, 20(4): 345–354. DOI:10.1109/TSM.2007.907607 |
| [18] | Lee S P, Chao A K, Tsung F, et al. Monitoring batch processes with multiple on-off steps in semiconductor manufacturing[J]. Journal of Quality Technology, 2011, 43(2): 142–157. DOI:10.1080/00224065.2011.11917852 |
| [19] | Martin E B, Morris A J. Non-parametric confidence bounds for process performance monitoring charts[J]. Journal of Process Control, 1996, 6(6): 349–358. DOI:10.1016/0959-1524(96)00010-8 |
| [20] | Lu N, Gao F, Yang Y, et al. PCA based modeling and online monitoring strategy for uneven-length batch processes[J]. Industrial & Engineering Chemistry Research, 2004, 43(13): 3343–3352. |
| [21] | Yu J. Multiway discrete hidden Markov model based approach for dynamic batch process monitoring and fault classification[J]. American Institute of Chemical Engineers Journal, 2012, 58(9): 2714–2725. DOI:10.1002/aic.12794 |



