0 引言
信号去噪和噪声抑制是当前信号处理领域研究的首要问题.在信号获取和传送过程中,不可避免地会混入干扰噪声,尤其是当原始信号比较微弱时,噪声会严重破坏真实信号的特性.如何有效地去除和抑制噪声对雷达信号、检测传感器、语音增强、医学信号等相关领域及后续的研究具有非常重要的意义.
传统的傅里叶变换去噪是通过傅里叶变换在频域上选择性地去除噪声信号.Donoho提出的小波阈值去噪算法是一种非线性分析去噪算法,呈现出良好的时频特性和多辨率分析特性[1],此后To等众多学者提出了大量的改进算法[2-6].另一种重要的信号去噪方法是基于线性变换的方法,Cheveigné等提出主成分分析法(principal component analysis,PCA)并用于医学信号消噪[7].主成分分析去噪效果与主成分的数目密切相关,选择保留合适的主成分分量达到去噪的目的[8-9].Mallat等提出的稀疏分解(sparse decomposition)去噪方法[10].稀疏分解通过对混有噪声的信号在过完备原子库上进行稀疏表示,仅用若干个较大的表示系数重构原信号,屏掉了部分小系数包含的噪声成分[11-12],从而实现信号的去噪,使信号更加简洁、自适应地表示成若干基的线性组合,比较全面细致地表征信号涵盖的某些特征,有效地将信号和噪声分离开来,广泛地应用于信号去噪领域[13-19].此外,赖联有等提出了量子随机滤波自适应学习算法,实现了对语音信号的去噪[20].在信号去噪领域,以上学者的研究取得了较好的效果,促进了去噪方法的发展;然而,在现有研究成果的基础上,如何进一步去除和抑制噪声干扰,仍为当前信号去噪领域研究的热点问题.
本文在现有的研究工作基础上,考虑到信号中不同的片段普遍存在相似性结构特征,提出了信号片段的定义,在此基础上,实现了基于信号片段相似性的去噪效果增强方法,能有效提高现有方法的去噪效果.与传统的均值去噪、中值去噪、高斯去噪等点估计方法相比,本方法从信号的整体考虑,把信号划分为若干待去噪片段,并在整个信号内寻找与待去噪片段结构相似的片段集合,然后基于该相似片段集合,实现原信号的去噪.因此,该方法被称为基于信号片段相似性的信号去噪.
1 基于片段相似性的去噪算法 1.1 相似片段的定义定义1 在一段信号Y =[y1,y2,…,yk,…,yN]中,N表示信号长度,yk表示第k(k∈[1,N])时刻采样值,则信号片段xi定义为xi=[yi,yi+1,…,yi+L-1]T,其中,i∈{1,2,3,…,N-L+1},L表示信号片段的长度.
在实际去噪过程中,L由信号的采样时间或者由信号的光滑性来确定:若信号比较光滑则相似片段的长度可以取得较大;反之,应该选取相对较短的信号片段.
定义2 若信号Y =[y1,y2,…,yk,…,yN]中存在信号片段xi与xj,其中i≠j,对于给定误差上界ε,满足:
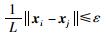
|
(1) |
则定义xj为xi的相似片段.
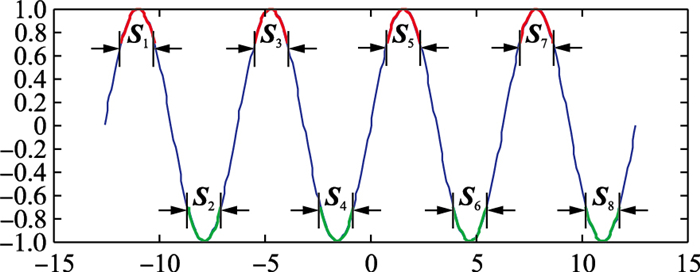
显然,根据以上定义,xi可能存在多个相似片段,则将xi的相似片段集合记为Xci={xi1,xi2,…,xiJ},其中J表示xi相似片段的个数.如图 1中,根据式(1)定义,S1的相似片段为S3、S5、S7,S2的相似片段为S4、S6、S8.
|
| 图 1 基本相似信号片段示例 Figure 1 An example of the basic similar signal segments |
然而由于式(1)定义的相似片段较为严格,这时考虑采用广义相似片段集合,如定义3所示.
定义3 若信号Y =[y1,y2,…,yk,…,yN]中存在信号片段xi与xj,其中i≠j,对于给定误差上界ε,满足:
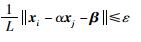
|
(2) |
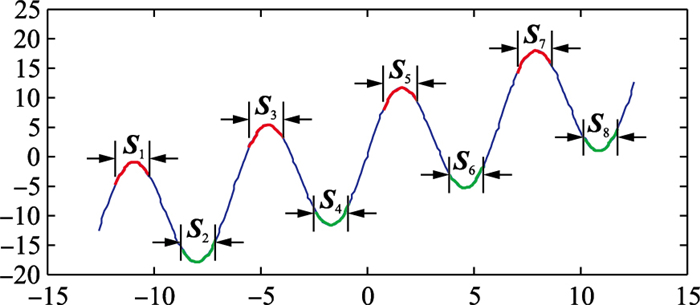
则定义xj为xi的广义相似片段.式(2)中,α表示信号片段之间存在的放大倍数关系;β表示由信号片段之间存在的常数偏差c组成的列向量,即β=[c,c,…,c]T,c为信号片段xj的均值与xi的均值之差;ε表示给定的误差上界.例如,图 2中,根据定义3可知,信号片段S1的广义相似片段为S3、S5和S7,即XS1=[x1S1,x2S1,x3S1],其中,x1S1=S3,x2S1=S5,x3S1=S7;S2的广义相似片段为S4、S6和S8,即XS2=[x1S2,x2S2,x3S2],其中,x1S2=S4,x2S2=S6,x3S2=S8.
|
| 图 2 广义相似片信号段示例 Figure 2 An example of the extend similar signal segments |
基于2.1节中关于相似片段的定义可知,设待去噪信号片段为xi,基于式(1)或式(2)可求得xi的相似片段集合为Xci,将集合中的元素以列向量形式重写为矩阵形式Xi=[xi1,xi2,…,xiJ],其中J表示相似片段的数量.考虑到随机噪声具有独立同分布的特性且噪声统计特性的均值为0,因而本文提出采用相似片段集合加权平均的方式来实现对原始信号的去噪,具体表示为
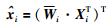
|
(3) |
式中,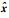
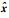
考虑到Wi主要度量相似片段与原始信号间的相似程度,因而本文根据信号片段间误差来确立各相似片段的权值Wi=[wi1,wi2,…,wiJ],具体表示为
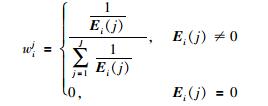
|
(4) |
式中,1≤j≤J,Ei=[ei1,ei2,…,eiJ],eij表示待去噪信号片段xi与其第j个相似片段的误差,具体方法为:
若根据定义2求得xi的相似片段集合Xci,则待去噪信号片段xi与其第j个相似片段的误差eij表示为
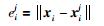
|
(5) |
若根据定义3求得xi的广义相似片段集合Xci,则待去噪信号片段xi与其第j个相似片段的差值eij表示为
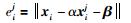
|
(6) |
综上,针对信号片段xi的相似信号片段求取,以及基于相似片段集合的去噪步骤归纳为:
步骤1 初始化参数α、β,容许误差ε,误差增量与集合数量调整参数Δε,相似片段集合大小J,相似片段的索引j=0,循环中间变量ki=1.
步骤2 计算xi的均值与待比较信号片段xki的均值之差c组成的偏差向量β=[c,c,…,c]T.判断‖xi -αxki-β ‖≤ε是否为真:若是,则令j=j+1,xij=xki,转至步骤3;否则,直接转至步骤3.
步骤3 判断ki < N-L+1是否为真:若是,则更新中间变量ki=ki+1,转至步骤2;否则,转至步骤4.其中,N表示整体信号长度,L表示信号片段长度.
步骤4 判断j≥J是否为真:若是,则转至步骤5;否则,重置ε=ε+Δε,令ki=1,j=0,转至步骤2.
步骤5 选取误差最小的前J个相似片段,按照式(6)计算相似片段与待去噪信号片段的误差向量Ei,转至步骤6.
步骤6 根据式(4)计算Ei对应的权值向量Wi=[wi1,wi2,…,wiJ],然后根据式(3)求得信号片段xi的去噪结果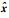
步骤7 结束.
以上步骤为信号片段基于广义相似片段的去噪算法流程.其中,步骤1为参数设置,步骤2~步骤4为相似片段的求取过程,步骤5~步骤6为信号片段的去噪过程.此外,对上述步骤作以下说明:
1) 将算法步骤5中的式(6)改为式(5),即可实现基本的相似片段去噪算法.
2) 上述步骤4中的Δε用于控制相似片段的数量.当相似片段数量少于设定值时,适当增加容许误差ε,即令ε=ε+Δε,以松弛信号相似性的条件,从而提高符合相似性条件的信号片段数量;若增加参数Δε后,仍不能够获得足够的相似片段数量,则可以适当减小信号片段长度L.除此之外,极端情况下,当原信号的数据量极少时,部分信号片段可能不存在相似片段.此时,该信号片段相当于没有改进,但是去噪效果也不会变差.
1.3 整体信号去噪原理与实施步骤在2.2节讨论的信号片段去噪方法基础上,本节主要讨论整体信号的去噪.由于整体信号的去噪与信号片段的划分密切相关且信号片段的划分主要分为无交集划分和有交集划分两种方式,因而整体信号的去噪亦分为两种方式:
1) 基于无交集信号片段的整体信号去噪.将信号Y按照式(7)划分:
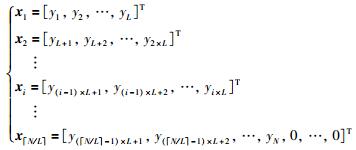
|
(7) |
式中,
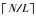
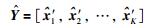
|
(8) |
式中,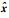
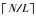
2) 基于k交集信号片段的整体信号去噪.针对基于无交集信号片段的整体信号去噪方法切断了片段端点间的相互关联,易出现脉冲震荡、平滑性差的问题,提出了有交集的信号片段划分方式:
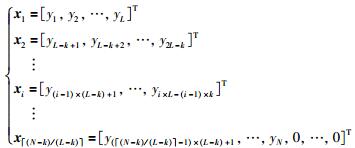
|
(9) |
如式(9)所示,因为相邻的相似片段之间有k个数据点相互重叠,所以称为k交集相似片段划分.此外,由式(9)可知第i个信号片段最后一个数据编号为i×L-(i-1)×k,进而可知,若N-k不能被L-k整除,则需要将原信号Y剩余的部分用0补齐.
针对有交集划分方式得到的信号片段xi,将其排列为矩阵形式X=[x1,x2,…,xK],K= 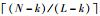
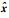
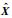
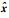
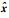
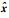
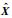
1) 令zi=0N×1,其中i=1,…,K.
2) 将zi中((i-1)×(L-k))至(i×L-(i-1)×k)之间的元素赋值为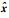
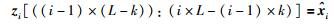
|
(10) |
3) 将zi组合成矩阵形式Z=[z1,z2,…,zK].
4) 基于Z计算整体信号的去噪结果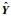
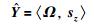
|
(11) |
其中,Ω和sz均为N维向量.由于yn可能包含在多个相似片段中并被多次去噪,因此sz表示所有信号片段中信号点yn的去噪结果之和,即sz(n)为Z的第n行之和:
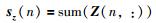
|
(12) |
各信号点yn的权值Ω(n)为yn出现在Z中频次Fre(yn)的倒数表示,即:
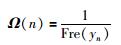
|
(13) |
通过对比式(7)~式(13)不难发现,当k交集相似片段划分方式中k=0时,k交集相似片段划分退化为无交集划分,因此无交集划分方式是k交集相似片段划分方式的一种特例.
总结以上去噪步骤并考虑到多步迭代能进一步增强去噪效果,整理原信号的去噪步骤为:
步骤1 初始化参数α、ε、Δε,计算整体信号长度N,确定信号片段长度L,相似片段集合大小J,相似片段的索引j=0,信号片段索引i=1,循环中间变量ki=1,循环计数器T=1,最大去噪处理次数TM.
步骤2 将预处理后的待去噪信号Y,按照式(7)或者式(9)划分信号片段得到[x1,x2,…,xi,…,xK]及信号片段的数量K,转至步骤3.
步骤3 若i≤K则计算第i个信号片段xi的去噪值,即执行2.2节中的信号片段的去噪算法,否则转至步骤4.
步骤4 对所有的去噪片段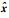
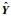
步骤5 若T < TM,则T=T+1,重新初始化j=0,i=1,循环中间变量ki=1,xi=zi,转至步骤3;否则,转至步骤6.
步骤6 结束.
大量实验结果表明,信号片段划分长度由原信号长度的0.1%~1%大致确定,信号片段的相似片段数量一般设置为10~50.对于相似结构较多的信号,相似片段的数量可以取得较大,如30左右.对于相似结构较少的信号,那么设置其相似片段数量在10~20之间比较合适.
1.4 去噪评价准则针对以上去噪方法效果的评价,本文采用均方误差(mean square error,MSE)和信噪比(signal to noise ratio,SNR)进行分析说明,若MSE越小且SNR越大,则说明滤波后信号越接近真实信号、滤波效果越好.以上两种评价准则的主要表述为:
MSE准则 设x(n)为未加噪声的原始信号,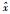
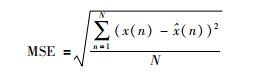
|
(14) |
SNR准则 设信号f(n)=x(n)+v(n),f(n)为x(n)的测量值,x(n)为未加噪声的原始信号,v(n)为噪声信号,N为信号长度,SNR定义为平均功率信噪比,即在持续时间内信号平均功率与噪声平均功率之比:
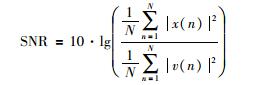
|
(15) |
为了测试方法的有效性,本文采用2个案例分别进行测试.2个案例均为处于工作状态的某机械系统信号,首先依次使用均值滤波、中值滤波、高斯滤波、小波阈值去噪、主成分分析去噪和稀疏表示去噪等6种去噪算法作为基础算法,在此基础上采用对应的片段相似性去噪和广义片段相似性去噪算法进行改善.其中均值滤波、中值滤波、高斯滤波均采用的基本滤波算法,小波阈值去噪使用2层分解软阈值处理,主成分分析采用文[21-22]中主成分分析的降噪方法,稀疏表示参考文[23]中随机字典的方法对信号去噪.
1) 测试信号Ⅰ:某型号电机工作的非线性偏移震动轨迹可采用如下信号进行模拟:
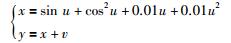
|
其中,u表示系统输入,x表示真实震动轨迹,y表示含有随机测量误差的震动轨迹测量值,v表示测量误差.
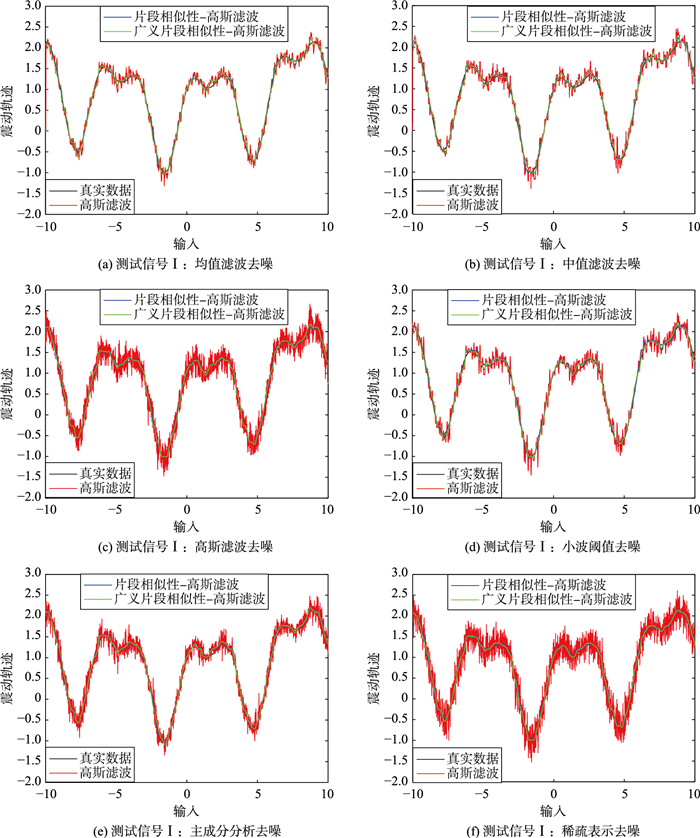
在本实验中,依据2.3节所述步骤,参数设置如下:采样间隔Δu=0.01,步骤2.3中的参数置为α=1,ε=0.5,Δε=0.1,相似片段的长度取L=30,相似片段集合大小为J=10,迭代次数TM=5,信号片段划分交集数k=L-1.系统输入u∈[-10, 10].经测试,测量信号y与真实震动轨迹x的均方误差MSE=0.299 83,信噪比SNR=12.159 17.针对该测试信号,为消除噪声v对测量结果的影响,采用6种算法对该测试信号进行去噪处理,并在此基础上采用本文提出的改进算法进一步改善去噪效果,结果如图 3所示.
|
| 图 3 测试信号Ⅰ的结果对比 Figure 3 Result comparison of the test signal Ⅰ |
图 3(a)~3(f)分别表示均值滤波、中值滤波、高斯滤波、小波阈值去噪、主成分分析去噪、稀疏表示去噪方法及其改进方法的效果图,其中黑线表示真实数据,红线表示原去噪算法结果,蓝线表示本文提出的基本片段相似性去噪去噪结果,绿线表示基于广义片段相似性的去噪结果.由图 3可见,基本的片段相似性去噪曲线和广义片段相似性去噪曲线分布于原去噪方法的包络线之内,其中图 3(d)中高斯滤波去噪、图 3(e)中主成分分析去噪与图 3(f)中稀疏表示去噪对应的基本的片段相似性去噪方法改进最为显著.由表 1去噪指标可知基于稀疏表示的广义片段相似性去噪算法达到最佳去噪效果(MSE=0.0478 7,SNR=28.096 26 dB),在该测试信号下,基本的片段相似性去噪算法的MSE比原方法平均降低了65.07%,SNR平均提高了54.58%,广义片段相似性去噪算法的MSE比原方法平均降低了66.17%,SNR平均提高了56.42%,并略优于基本的片段相似性去噪算法.同时,由结果可知,两种方法均有效提高了信噪比,降低了均方误差.
| MSE对比 | SNR对比 | ||||||
| 去噪方法 | 原方法 | 基本相似性 | 广义相似性 | 去噪方法 | 原方法 | 基本相似性 | 广义相似性 |
| 均值 | 0.146 57 | 0.055 17 | 0.056 18 | 均值 | 18.375 90 | 26.862 61 | 26.705 57 |
| 中值 | 0.164 40 | 0.066 00 | 0.062 96 | 中值 | 17.378 77 | 25.305 76 | 25.715 97 |
| 高斯 | 0.187 00 | 0.057 95 | 0.058 43 | 高斯 | 16.259 79 | 26.435 62 | 26.364 56 |
| 小波 | 0.145 34 | 0.059 33 | 0.056 08 | 小波 | 18.448 92 | 26.230 74 | 26.720 07 |
| 主成分 | 0.150 50 | 0.053 28 | 0.051 69 | 主成分 | 18.146 12 | 27.164 79 | 27.428 12 |
| 稀疏表示 | 0.215 72 | 0.052 98 | 0.047 87 | 稀疏表示 | 15.018 74 | 27.213 79 | 28.096 26 |
2) 测试信号Ⅱ:模拟某机械部件工作时角度变化的周期性信号为
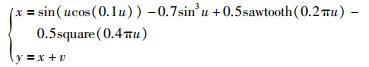
|
其中,sawtooth(·)表示锯齿波函数,square(·)表示方波函数,v表示测量误差,u表示系统输入,x表示角度的变化量,y表示混入噪声后x的实际测量值.
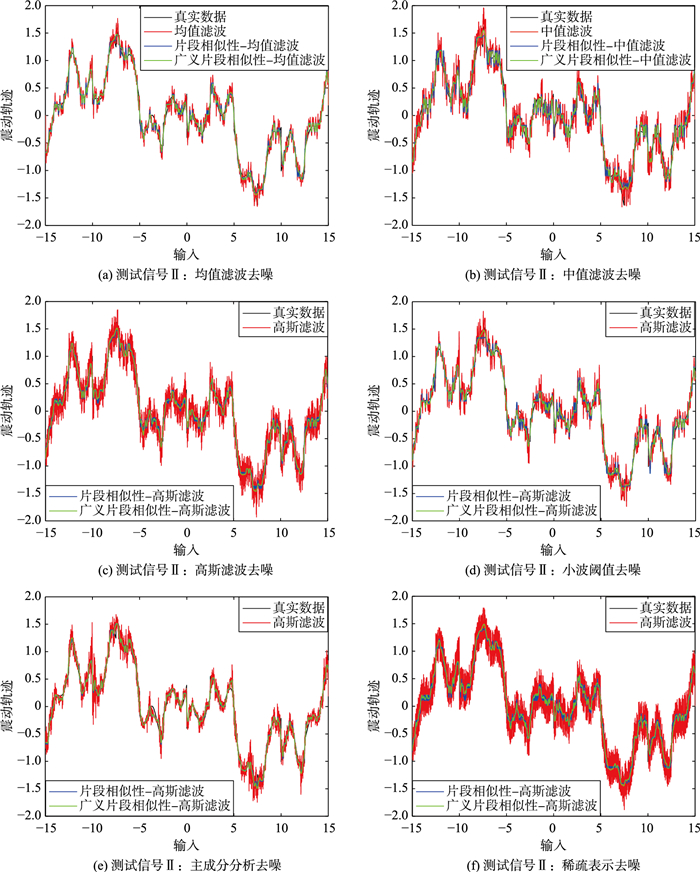
设置采样间隔Δu=0.01,系统输入u∈[-15, 15],测量信号y的MSE=0.291 10,信噪比SNR=7.294 35.步骤2.3中的参数置为α=1,ε=0.5,Δε=0.1,相似片段的长度取L=10,相似片段集合大小为J=20,迭代次数TM=5,信号片段划分交集数k=L-1.针对该信号,6种去噪方法及其增强算法的效果如图 4所示.图 4(a)~4(f)分别表示均值滤波、中值滤波、高斯滤波、小波阈值去噪、主成分分析去噪、稀疏表示去噪的效果图,其中黑线为真实数据,红线为原去噪算法的去噪结果,蓝线为基本的片段相似性去噪算法结果,绿线表示广义片段相似性去噪算法的去噪结果.由图 4可见6种去噪方法对应的基本的片段相似性去噪曲线和广义片段相似性去噪曲线分布于原去噪方法的包络线之内,其中图 4(d)中高斯滤波去噪与图 4(f)中稀疏表示去噪对应的基本片段相似性去噪方法改进最为显著,去噪信号曲线与真实信号曲线接近,较好地去除原去噪方法的毛刺,达到进一步去噪的效果.根据表 2中去噪数据,最高信噪比与最低均方差是基于稀疏表示的广义片段相似性去噪方法(MSE=0.074 48,SNR=19.134 81 dB),基本的片段相似性去噪算法MSE比原方法平均降低了39.69%,SNR平均提高了37.80%,广义片段相似性去噪算法的MSE比原方法平均降低了37.80%,SNR平均提高了47.31%,两种定义的片段相似性去噪方法均改进了原去噪方法且广义的片段相似性去噪方法优于基本的片段相似性去噪算法.
|
| 图 4 测试信号Ⅱ结果对比 Figure 4 Result comparison of the test signal Ⅱ |
| MSE对比 | SNR对比 | ||||||
| 去噪方法 | 原方法 | 基本相似性 | 广义相似性 | 去噪方法 | 原方法 | 基本相似性 | 广义相似性 |
| 均值 | 0.118 21 | 0.089 00 | 0.080 17 | 均值 | 15.121 94 | 17.587 41 | 18.494 53 |
| 中值 | 0.197 42 | 0.125 30 | 0.106 60 | 中值 | 10.810 48 | 14.616 05 | 16.020 03 |
| 高斯 | 0.180 44 | 0.087 61 | 0.079 96 | 高斯 | 11.448 52 | 17.724 51 | 18.518 06 |
| 小波 | 0.150 04 | 0.098 48 | 0.080 43 | 小波 | 13.050 83 | 16.708 68 | 18.466 99 |
| 主成分 | 0.128 77 | 0.078 93 | 0.077 27 | 主成分 | 14.378 97 | 18.629 92 | 18.814 93 |
| 稀疏表示 | 0.191 37 | 0.091 10 | 0.074 48 | 稀疏表示 | 10.672 68 | 17.384 55 | 19.134 81 |
实验结果证实了基于信号片段相似性去噪算法能够增强原去噪方法的去噪效果.
3 结论本文考虑了原始信号内部信号片段之间的相似性关系,在基于现有算法的去噪结果上,利用信号内部的相似片段,提出了信号片段相似性和广义信号片段相似性定义并基于信号的相似特征,提出了基于片段相似性的信号去噪算法.最后采用2个测试信号,对算法的有效性进行了验证.仿真结果表明:基本的片段相似性去噪方法在原去噪方法的基础上MSE分别降低了约65%和37%,SNR分别提高了55%和38%;广义片段相似性去噪方法MSE分别降低了66%和38%,SNR分别提高了56%和47%,验证了本文所提方法的有效性和可行性,表明本研究成果对于工程实践具有非常重要的指导意义.
此外,需要注意的是,当信号噪声为非零均值噪声时,则需要先获取噪声的统计特性,然后在处理过程中减去噪声的均值.此外,本文根据整体数据长度和经验,选择了合适的信号片段长度,然而如何根据信号特征,自适应的选择最佳信号片段划分长度或相似片段集合大小,将是下一步研究的重点.
| [1] | Donoho D L. De-noising by soft-thresholding[J]. IEEE Transactions on IT, 1995, 41(3): 612–627. |
| [2] | To A C, Moore J R, Glaser S D. Wavelet denoising techniques with applications to experimental geophysical data[J]. Signal Processing, 2009, 89(2): 144–160. DOI:10.1016/j.sigpro.2008.07.023 |
| [3] |
蒋克荣, 唐向清, 朱德泉.
基于改进阈值小波算法的汽车轮速信号处理[J]. 仪器仪表学报, 2010, 31(4): 736–740.
Jiang K R, Tang X Q, Zhu D Q. Automobile wheel speed signal processing based on wavelet algorithm of improved threshold[J]. Chinese Journal of Scientific Instrument, 2010, 31(4): 736–740. |
| [4] |
杨恢先, 王绪四, 谢鹏鹤, 等.
改进阈值与尺度间相关的小波红外图像去噪[J]. 自动化学报, 2011, 37(10): 1167–1174.
Yang H X, Wang X S, Xie P H, et al. Infrared image denoising based on improved threshold and inter-scale correlations of wavelet transform[J]. Acta Automatica Sinica, 2011, 37(10): 1167–1174. |
| [5] | Khan S, Jain A, Khare A, et al. Denoising of images based on different wavelet thresholding by using various shrinkage methods using basic noise conditions[J]. International Journal of Engineering, 2013, 2(1): 1–6. |
| [6] |
唐国维, 张岩, 王苫社, 等.
基于Contourlet方向滤波优化的SPECK图像编码算法[J]. 信息与控制, 2015, 44(6): 641–647.
Tang G W, Zhang Y, Wang S S, et al. SPECK image coding algorithm based on Contourlet direction filtering optimization[J]. Information and Control, 2015, 44(6): 641–647. |
| [7] | Cheveigné A D, Simon J Z. Denoising based on time-shift PCA[J]. Journal of Neuroscience Methods, 2007, 165(2): 297–305. DOI:10.1016/j.jneumeth.2007.06.003 |
| [8] | Verbanck M, Josse J, Husson, et al. Regularised PCA to denoise and visualise data[J]. Statistics & Computing, 2013, 25(2): 471–486. |
| [9] | Salmon J, Harmany Z, Deledalle C A, et al. Poisson noise reduction with nonlocal PCA[J]. Computer Science, 2012, 48(2): 1109–1112. |
| [10] | Mallat S G, Zhang Z. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397–3415. |
| [11] | Needell D, Tropp J A. CoSaMP:Iterative signal recovery from incomplete and inaccurate samples[J]. Applied & Computational Harmonic Analysis, 2008, 26(3): 301–321. |
| [12] | Dai W, Milenkovic O, Milenkovic. Subspace pursuit for compressive sensing signal reconstruction[J]. IEEE Transactions on Information Theory, 2009, 55(5): 2230–2249. |
| [13] | Zhang L, Rastislav L, Wu X L. PCA-based spatially adaptive denoising of CFA images for single-sensor digital cameras[J]. IEEE Transaction on Image Processing, 2009, 18(4): 797–812. DOI:10.1109/TIP.2008.2011384 |
| [14] | Baraniuk R G, Cevher V, Duarte M F, et al. Model-based compressive sensing[J]. IEEE Transactions on Information Theory, 2010, 56(4): 1982–2001. DOI:10.1109/TIT.2010.2040894 |
| [15] | Eldar Y C, Kuppinger P, Bölcskei H. Compressed sensing of block-sparse signals:Uncertainty relations and efficient recovery[J]. Mathematics, 2009, 58(6): 3042–3054. |
| [16] | Yin H T, Li S T, Fang L Y. Block-sparse compressed sensing:Non-convex model and iterative re-weighted algorithm[J]. Inverse Problems in Science and Engineering, 2013, 21(1): 1–14. |
| [17] | Li S, Yin H, Fang L. Group-sparse representation with dictionary learning for medical image denoising and fusion[J]. IEEE Transactions on Biomedical Engineering, 2012, 59(12): 3450–3459. DOI:10.1109/TBME.2012.2217493 |
| [18] |
宋和平, 王国利.
稀疏信号重构的残差最小化追踪[J]. 信息与控制, 2014, 43(6): 722–726, 734.
Song H P, Wang G L. Sparse signal recovery via residual minimization pursuit[J]. Information and Control, 2014, 43(6): 722–726, 734. |
| [19] |
刘涵, 梁莉莉, 黄令帅.
基于分块奇异值分解的两级图像去噪算法[J]. 自动化学报, 2015, 41(2): 439–444.
Liu H, Liang L L, Huang L S. Two-stage image denoising using patch-based singular value decomposition[J]. Acta Automatica Sinica, 2015, 41(2): 439–444. |
| [20] |
赖联有, 金福江, 吴浩瀚.
语音信号的量子随机滤波降噪方法[J]. 信息与控制, 2015, 44(5): 598–603.
Lai L Y, Jin F J, Wu H H. Speech de-noising method using quantum stochastic filter[J]. Information and Control, 2015, 44(5): 598–603. |
| [21] |
王文波, 张晓东, 汪祥莉.
基于主成分分析的经验模态分解消噪方法[J]. 电子学报, 2013, 41(7): 1425–1430.
Wang W B, Zhang X D, Wang X L. Empirical mode decomposition de-noising method based on principal component analysis[J]. Acta Electronica Sinica, 2013, 41(7): 1425–1430. |
| [22] |
余昌和, 李建黎.
低信噪比下相干信号的DOA估计的白噪声滤除方法[J]. 信号处理, 2012, 28(7): 957–962.
Yu C H, Li J L. A white noise filtering method for DOA estimation of coherent signals under low SNR[J]. Signal Processing, 2012, 28(7): 957–962. |
| [23] | Elad M, Yavneh I. A plurality of sparse representations is better than the sparsest one alone[J]. IEEE Transactions on Information Theory, 2009, 55(10): 4701–4714. |



