0 引言
近年来,各种重特大突发事件不断发生(如汶川地震、天津港大爆炸、台湾地震等),给国家和人民带来巨大损失,引起政府部门的高度重视.由于非常规突发事件具有动态性、复杂性和不可预测性的特点[1-2],相应的应急响应决策方案通常面临各种不同的情景,需要综合考虑不同情景下的方案实施效果,因此应急决策问题多具有风险决策的特点.风险型应急决策是指在不确定条件下,对各种突发事件进行判断并采取非常规应急措施,但决策结果难以预料,具有多种可能性的决策.
目前国内外学者关于风险应急决策的研究主要集中在3个方面:
1) 考虑决策者心理行为的风险型应急决策方法.袁媛等[3]从后悔理论的思想考虑,提出了一种针对存在多种可能情景且各情景发生的概论随实施方案不同而变化的考虑后悔规避的应急风险决策方法.王亮等[4]基于前景理论的思想,通过比较实时损失和心理参考点来动态调整应急决策方案,提出一种基于前景理论的动态应急决策方法.Liu等[5]考虑决策者后悔规避的特点,通过构建决策者心理依赖参照点,提出一种基于累积前景理论的应急风险决策方法.程铁军等[6]针对不完全信息下的应急响应风险决策问题,通过综合考虑决策者的有限理性、损失敏感、易受突发事件相关因素影响的特征,提出了一种基于累积前景理论的区间多属性应急风险决策方法.陈业华等[7]综合考虑了决策者心理感知的效用价值和结果情景发生的概率两个属性,通过对决策者的动态参照点和心理感知的分析,构建一种基于效用风险熵的应急决策动态调整方法.
2) 考虑风险特征和风险成因的风险型应急决策方法.Xu等[8]针对自然灾害风险应急决策问题,通过分析突发事件中的风险特征和风险成因,构建了应急决策风险消除协调框架,提出了一种风险逐渐稳定与风险水平足够低的应急救援决策方案.Liu等[9]针对风险应急决策的特点,提出了一种基于故障树分析的风险应急决策方法.Zhou[10]在事故应急响应风险决策中,通过考虑风险决策的动态性和风险特性,提出了基于模糊故障树分析方法(FFTA)的工作系统事故应急反应风险决策方法.谢非等[11]运用解释结构模型(ISM)对构建企业汇率风险应急机制及其影响因素进行分析研究,构建企业汇率风险应急机制,对企业汇率风险应急管理实践提供实用路径.
3) 基于数学理论和决策模型的风险型应急决策方法.江时雨等[12]在突发事件应急方案选择中考虑信息不确定和随机性的特征,提出了一种基于贝叶斯和蒙特卡洛的应急风险决策方法.Dillon等[13]采用多属性效用理论来解决安全风险分析中一些最常见的问题,并以美国海军资产评估为实例,提出了一种反恐措施的风险型应急决策方法.Sun等[14]通过定义和分析模糊事件的条件概率,将概率方法引入粗糙集中,提出了一种模糊粗糙集在空间上概率逼近的应急决策方法.
上述研究虽然从不同方面对风险型应急决策进行了研究,但未能考虑风险应急决策过程涉及的决策人数众多、人员结构复杂(通常来自不同部门和领域,代表不同的利益群体)、偏好冲突高且难以达成高一致性目标的问题,这种决策往往形成大群体决策[15-16].而且,在大群体决策过程中,少有文献考虑决策成员的心理行为和对风险的敏感程度.因此,本文构建一种基于冲突风险熵和后悔规避的大群体应急决策方法.决策成员在面临复杂应急决策问题时难以对突发事件的状态做出全面、准确的判断且承受巨大的心理压力,往往表现出不完全理性、损失敏感、对某些准则有一定主观期望要求等特征.本文首先从决策成员心理行为角度出发,在决策成员为“有限理性人”[17]的假设的前提下,考虑决策成员的风险规避行为.依据后悔理论,计算决策成员对每个方案在每种状态下的后悔值和期望值;在此基础上,对决策成员偏好进行聚类,根据多数原则和决策者对决策贡献程度的不同赋予决策成员不同的权重并利用相似度对其加以修正;考虑到大群体决策中不可避免地会出现冲突[18-20],因此引入风险熵[21]对应急决策过程中由群体冲突产生的风险进行测度;在此基础上,提出决策方案排序方法.
1 方法原理 1.1 问题描述记X={x1,x2,…,xp}表示p个决策备选方案,其中xl(l=1,2,…,p)表示第l个备选方案;记C={c1,c2,…,cn}表示方案的n个属性,其中cj(j=1,2,…,n)表示第j个属性;记E={e1,e2,…,em}表示m个决策成员,其中ei(i=1,2,…,m)表示第i个决策成员.由于决策成员众多,为了降低大群体偏好信息的规模,对大群体成员偏好进行聚类,形成K个聚集,设聚集Ck中成员数为nk,满足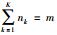
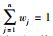
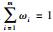
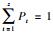
本文需要解决的问题是:对于由重特大突发事件引起的大群体应急决策问题,依据相关信息,在考虑决策成员心理行为的情况下,如何解决大群体成员权重确定和决策冲突测度的问题,在尽可能符合现实决策成员心理感知和减少信息失真的条件下,得到有效的决策方案排序结果.
1.2 感知效用矩阵的计算Bell[22]、Loomes和Sugden[23]等将后悔理论引入不确定情况下的理性选择可以解释许多违背期望效用理论的现象,后悔理论假设决策者是理性的,但他们在决策过程中不仅仅只考虑收益回报(价值),还考虑预期的后悔值,即决策者会对自己所处的现实情景与可能发生的情景(决策者在过去选择其它备选方案)进行比较:如果决策者自省时发现自己选择其它备选方案可以得到更好的结果,那么内心会感到后悔;反之,就会感到欣喜.因此,决策者在决策过程中会预期考虑决策结果可能产生的后悔值或欣喜值,并在实际生活中会尽量避免选择可能导致后悔的决策方案,即决策者是后悔规避的.后悔理论假设决策者的感知效用值由两个部分组成,即当前效用值和后悔—欣喜值.下面给出感知效用矩阵的具体计算过程:
为了消除不同物理量纲对决策结果的影响,对风险决策信息矩阵Y =[yljit]p×m×n×z进行规范化处理(其中yljitU和yljitL分别表示初始决策信息yljit的上、下界),得到规范化矩阵A =[aljit]p×m×n×z,根据属性类型的不同,分为效益型和成本型,具体方法为:
当j为效益型指标时,规范化公式如式(1)所示;当j为成本型指标时,规范化公式如式(2)所示.
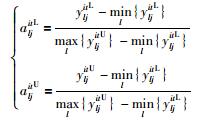
|
(1) |
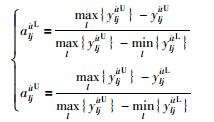
|
(2) |
根据规范化矩阵A计算属性的效用值,由于决策过程中决策成员通常都是风险厌恶的,因此决策成员的效用函数为严格递增的凹函数,这里采用幂函数[24]模拟效用函数:
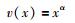
|
(3) |
其中,α表示决策成员的风险厌恶系数,满足0 < α < 1.当α越小时,决策成员对于风险的厌恶程度越高;反之,决策成员对风险的厌恶程度越低.
设属性值在规范化矩阵A的决策区间信息[aljitL,aljitR]上随机取值(其中aljitU和aljitL分别表示规范化决策信息aljit的上、下界),服从均匀分布[25],得属性值aljit的随机概率密度函数fljit(x):
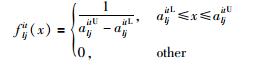
|
(4) |
综合式(3)和式(4),求得决策成员ei针对方案xl在状态st下的属性cj的效用值uljit:
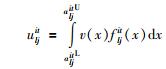
|
(5) |
根据后悔理论,利用式(5)求得的效用值构建后悔—欣喜函数R(Δu):
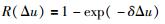
|
(6) |
其中,δ是后悔厌恶系数,δ∈[0,+∞),δ越大,则后悔规避程度也越高;Δu=ul1jit-ul2jit,表示决策成员ei在状态st下针对方案xl1和xl2的属性cj的效用值之差.当R(Δu)>0时,表示决策成员心理是后悔的;当R(Δu) < 0时,表示决策成员心理是欣喜的;当R(Δu)=0时,此时决策成员心理既不后悔也不欣喜,两个方案无差异.
由式(6)得到决策成员ei针对方案xl在状态st下的属性cj相对于最优状态(同一属性下所得到的最大效用值所对应的状态点,表示决策者针对某一属性指标在此状态下所能得到的最大效用值)的后悔—欣喜值公式为
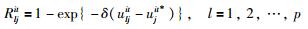
|
(7) |
其中,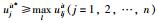
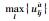
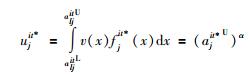
|
(8) |
其中,aljit*U为状态st下属性cj的最优点,即状态st下属性cj的理想点.由于uljit≤ujit*,因此Rljit≤0,故Rljit为后悔值.
综合式(7)和式(8)可求得后悔值Rljit=1-exp{-δ(uljit-ujit*)},再利用式(5)可求得感知效用值bljit=uljit+Rljit和感知效用矩阵B =[bljit]p×m×n×z.
1.3 决策成员权重的确定1) 决策成员感知效用矩阵聚类
利用属性权重wj(通过事先评估或经验已给出)集结不同状态下的属性值bljit,将感知效用矩阵B=[bljit]p×m×n×z集结成矩阵Blit=[blit]p×z,集结公式为
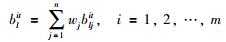
|
(9) |
根据集结矩阵计算两个决策成员ei1和ei2的感知效用矩阵之间的相离度,计算公式为
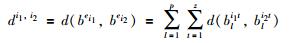
|
(10) |
其中,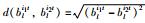
引入阈值γ(0 < γ < 1),利用聚类算法[26]和聚类算法矩阵D=[di1,i2]m×m将集结后的矩阵Blit聚类成偏好大体接近的聚集Ck(1≤k≤K),阈值γ的大小决定决策成员ei能否进入聚集Ck(其中,nk表示聚集Ck中的成员数,满足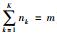
2) 决策成员权重的确定
根据聚类结果确定聚集偏好矩阵和成员的初始权重.由于处于同一聚集内部的成员给出的偏好接近,因此把同一聚集内部成员的权重赋予相同的值.基于多数原则,聚集内部成员数量多则其成员赋予较大的权重值;反之,成员数量少则其成员权重值也相应较小.所以,ωnk与nk成正比,即ωnk=θnk(其中θ为比例系数).又因满足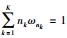
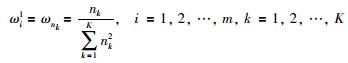
|
(11) |
同时,可以求得聚集偏好矩阵Gk:
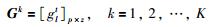
|
(12) |
其中Gk表示聚集Ck内部各成员的平均矩阵,即glt=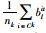
对于风险决策而言,决策成员的权重直接影响到决策的结果,进行方案排序时应尽量反映所有专家的初始意见.由式(11)可以求出各个决策成员的权重,此时假设的是聚集内部各成员权重一致,但在实际中即使处于同一聚集内的成员偏好之间也存在偏差,其意见也不完全一致,同一聚集内部各成员提供的信息也不完全一样,所做的贡献大小也不一样,所以同一聚集内部各成员的权重应进行进一步的调整,这里定义聚集Ck内部成员ei的感知效用矩阵Blit=[blit]p×z与其所在聚集偏好矩阵Gk的距离为
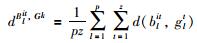
|
(13) |
其中,d(blit,glt)表示决策成员ei的偏好矩阵Blit与其所在聚集偏好矩阵Gk之间的欧氏距离.
对聚集Ck内部各成员权重的偏差度进行集结,得到聚集Ck内成员综合权重偏差度ϑk:
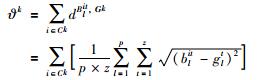
|
(14) |
定义聚集内部成员ei与聚集偏好矩阵Gk的相似度:
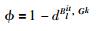
|
(15) |
由式(14)可知0≤dBlit,Gk≤1,则0≤ϕ≤1;又因Gk是聚集Ck内部各成员的平均矩阵,因此聚集内部各偏好矩阵到平均矩阵之间的距离和为1,则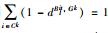
由于同一聚集内部成员偏好具有相似性,因此同一聚集内部成员ei与其聚集偏好矩阵Gk的偏差度越小越好,其赋予的权重也越大,由此得到聚集Ck内部成员ei的权重修正公式:
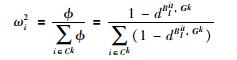
|
(16) |
由式(16)可知满足ωi2∈[0, 1],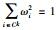
结合式(11)得到最终决策成员权重:
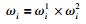
|
(17) |
由于在大群体决策聚类过程中,决策成员偏好与聚集偏好之间会产生冲突,导致决策初始信息的失真,影响决策结果.因此,这里引入熵对由冲突导致的风险进行测度.
定义决策成员ei的感知效用矩阵Blit=[blit]p×z与其所在聚集矩阵Gk=[glt]p×z关于方案xl在状态st下的冲突水平π(Blit):
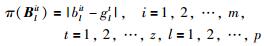
|
(18) |
π(Blit)表示决策成员偏好与其所在聚集偏好之间差异,π(Blit)越大,说明决策成员与其所在聚集之间意见差异越大,决策信息失真度越大.因此,需要对冲突导致信息失真的风险进行测度,以尽量降低由大群体偏好冲突造成的信息失真风险.由式(18)及聚集偏好矩阵Gk的定义可知,0≤π(Blit)≤1且有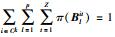
在由应急问题产生的大群体风险决策过程中,由决策成员偏好和聚集偏好之间产生的冲突导致信息失真的风险是无法避免且不可忽略的,并且应急决策的风险也与结果状态的不确定性相关.因此,在同一聚集内,将决策冲突和结果状态的概率考虑到风险决策中更合理.对此,引入冲突系数τlit(考虑到冲突越小越好),其计算公式为
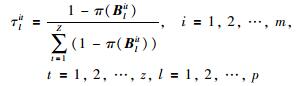
|
(19) |
定义冲突风险系数βlit(表示决策成员ei关于方案xl在状态st下的风险系数):
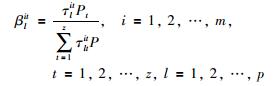
|
(20) |
由式(20)分析可知,0≤βlit≤1且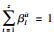
基于风险熵,得到决策成员在状态st下的冲突风险函数Risk(βlit,Pt):
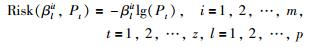
|
(21) |
由式(21)定义的冲突风险函数Risk(βlit,Pt)测度了决策成员在不同阈值下关于不同方案在不同状态下的冲突风险大小,该值越大,表示由冲突产生的风险越高.它不仅定量化了决策成员的初始偏好和其所在聚集偏好之间的冲突风险,同时也测度了决策方案产生不同状态结果的风险.
在式(21)的基础上,定义决策成员ei关于方案xl的冲突风险熵Hli:
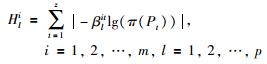
|
(22) |
定义的式(22)为决策成员ei关于方案的xl的冲突风险熵,它是一个确定量,反映的是决策成员ei关于方案xl的感知效用与其所在聚集偏好的不确定性程度.由于最终的决策信息取决于聚集偏好信息,因此决策成员的偏好信息与其所在聚集偏好信息之间的冲突会给最终的决策结果带来不确定性.这里,将冲突风险熵考虑到决策过程中,由式(22)得到决策成员ei关于方案xl的冲突风险权重hli:
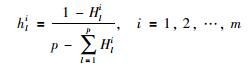
|
(23) |
利用决策成员权重ωi和冲突风险权重hli得到方案排序向量O =[O1,O2,…,Op]T,其中Ol:
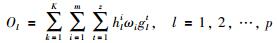
|
(24) |
综上所述,基于冲突风险熵和后悔规避的大群体应急决策过程为:
步骤1 根据式(1)和式(2)将初始风险型决策矩阵规范化,得到规范化矩阵A=[aljit]p×m×n×z.
步骤2 根据式(3)~式(8)求得每个决策成员的感知效用矩阵B=[bljit]p×m×n×z.
步骤3 根据式(9)~式(12)对集结后的感知效用矩阵Blit=[blit]p×z进行聚类,得到聚集偏好矩阵Gk=[glt]n×z和决策成员的初始权重ωi1.
步骤4 根据式(13)~式(17)求得决策成员的修正权重ωi2,从而确定决策成员的最终权重ωi.
步骤5 根据式(18)~式(23)求得同一聚集内部决策成员偏好与其所在聚集偏好之间的冲突风险熵,从而确定决策成员ei关于方案的xl的冲突风险权重hli.
步骤6 根据式(24)对方案进行排序.
2 算例分析本文以传染病疫情防控应急决策问题为例.假设某地区出现了1名类似某传染病的疑似感染者,由于该地区人口密度大,容易造成大面积的感染.为确保居民的身体健康、防止疫情大面积扩散而造成不可挽回的损失,应急部门迅速针对实时掌握的信息制定了5个应急方案.方案x1为对该名疑似感染者及其接触人员进行隔离;方案x2为对该名疑似感染者及其接触人员进行隔离,并对其活动区域进行重点消毒,其它区域也采取相应的消毒防范措施;方案x3为对该名疑似感染者及其接触人员进行隔离,对其活动区域进行重点消毒,其它区域也采取相应的消毒防范措施,并对该传染病进行病原研究;方案x4为对该名疑似感染者及其接触人员进行隔离,并对该传染病进行病原研究;方案x5为对该名疑似感染者及其接触活动区域进行消毒防治.并从相关部门调取12名专家(e1,e2,…,e12)从3个方面对应急方案进行决策:c1为预期挽救人员数目(效益型);c2为预期挽救的经济损失(效益型);c3为预期花费成本(成本型).为了计算方便,这里将所有属性定量化成统一形式(单位为万元),属性权重分别为:ω1=0.3,ω2=0.4,ω3=0.3.受掌握信息的有限性及传染病病毒多变性的影响,方案实施可能产生3种状态集{s1:优,s2:良,s3:差},其发生的概率分别为:0.4、0.4、0.2.各专家给出的各方案决策偏好信息如表 1所示.
| 方案 | s1 | s2 | s3 | ||||||
| c1 | c2 | c3 | c1 | c2 | c3 | c1 | c2 | c3 | |
| e1, x1 | [600, 700] | [550, 600] | [50, 55] | [550, 600] | [500, 600] | [50, 55] | [500, 600] | [450, 550] | [85, 90] |
| x2 | [650, 680] | [600, 650] | [35, 50] | [620, 650] | [580, 620] | [60, 160] | [570, 610] | [550, 580] | [80, 90] |
| x3 | [650, 700] | [600, 680] | [25, 30] | [600, 680] | [550, 650] | [55, 65] | [550, 600] | [500, 570] | [75, 80] |
| x4 | [605, 655] | [580, 640] | [30, 50] | [560, 600] | [520, 580] | [60, 70] | [530, 580] | [510, 550] | [80, 90] |
| x5 | [580, 620] | [570, 610] | [35, 45] | [520, 580] | [510, 540] | [55, 65] | [500, 530] | [470, 520] | [85, 90] |
| e2, x1 | [215, 220] | [190, 210] | [45, 55] | [200, 210] | [185, 190] | [65, 85] | [160, 175] | [70, 105] | [100, 130] |
| x2 | [210, 220] | [180, 190] | [35, 65] | [200, 205] | [180, 185] | [65, 95] | [160, 175] | [60, 90] | [115, 140] |
| x3 | [210, 215] | [175, 190] | [30, 60] | [195, 210] | [170, 185] | [70, 90] | [155, 160] | [75, 110] | [100, 125] |
| x4 | [205, 215] | [175, 180] | [25, 55] | [190, 205] | [170, 185] | [75, 90] | [150, 160] | [90, 115] | [95, 120] |
| x5 | [200, 210] | [165, 180] | [30, 60] | [185, 200] | [160, 175] | [70, 90] | [145, 160] | [60, 80] | [100, 125] |
| e3, x1 | [100, 120] | [50, 80] | [45, 55] | [100, 110] | [70, 85] | [60, 85] | [80, 100] | [50, 70] | [80, 90] |
| x2 | [140, 160] | [100, 120] | [45, 50] | [105, 125] | [90, 105] | [55, 65] | [85, 105] | [55, 65] | [75, 90] |
| x3 | [150, 165] | [140, 150] | [40, 45] | [110, 120] | [100, 110] | [50, 70] | [90, 105] | [70, 85] | [80, 90] |
| x4 | [165, 175] | [150, 155] | [30, 35] | [120, 135] | [115, 125] | [60, 70] | [100, 110] | [75, 90] | [75, 80] |
| x5 | [170, 180] | [150, 160] | [35, 55] | [135, 150] | [105, 120] | [70, 85] | [105, 115] | [100, 110] | [75, 80] |
| e4, x1 | [850, 900] | [700, 800] | [350, 400] | [650, 700] | [600, 700] | [350, 400] | [500, 600] | [400, 500] | [550, 600] |
| x2 | [750, 850] | [700, 800] | [300, 400] | [650, 700] | [600, 650] | [350, 400] | [550, 600] | [500, 600] | [500, 650] |
| x3 | [800, 900] | [750, 850] | [250, 300] | [700, 750] | [600, 700] | [350, 400] | [500, 550] | [500, 550] | [550, 600] |
| x4 | [700, 800] | [650, 700] | [300, 400] | [640, 700] | [550, 600] | [400, 500] | [450, 550] | [400, 420] | [550, 600] |
| x5 | [750, 800] | [700, 750] | [350, 400] | [650, 750] | [600, 650] | [450, 500] | [500, 600] | [400, 550] | [600, 660] |
| | |||||||||
| e9, x1 | [315, 335] | [295, 315] | [70, 90] | [270, 300] | [255, 275] | [90, 100] | [145, 170] | [125, 140] | [120, 145] |
| x2 | [315, 330] | [285, 310] | [80, 100] | [270, 290] | [240, 265] | [95, 115] | [145, 165] | [130, 145] | [115, 130] |
| x3 | [320, 350] | [300, 320] | [70, 90] | [280, 310] | [275, 300] | [80, 95] | [155, 185] | [140, 160] | [100, 115] |
| x4 | [300, 315] | [280, 300] | [115, 125] | [250, 275] | [220, 230] | [95, 155] | [130, 150] | [110, 125] | [130, 160] |
| x5 | [310, 320] | [285, 300] | [90, 110] | [265, 290] | [220, 240] | [99, 120] | [130, 155] | [115, 130] | [125, 145] |
| e10, x1 | [850, 900] | [700, 800] | [350, 400] | [650, 700] | [600, 700] | [350, 400] | [500, 600] | [400, 500] | [550, 700] |
| x2 | [90, 1000] | [800, 900] | [200, 250] | [750, 800] | [650, 700] | [300, 350] | [550, 600] | [500, 600] | [500, 550] |
| x3 | [800, 900] | [750, 850] | [250, 300] | [700, 750] | [600, 700] | [350, 400] | [450, 550] | [450, 500] | [550, 600] |
| x4 | [800, 950] | [700, 850] | [250, 300] | [640, 750] | [550, 600] | [350, 400] | [450, 550] | [450, 500] | [500, 600] |
| x5 | [800, 900] | [700, 850] | [300, 400] | [700, 750] | [600, 650] | [450, 500] | [500, 650] | [400, 550] | [600, 700] |
| e11, x1 | [140, 150] | [110, 120] | [50, 55] | [120, 135] | [50, 55] | [99, 155] | [110, 125] | [90, 110] | [85, 90] |
| x2 | [120, 135] | [75, 95] | [35, 50] | [80, 100] | [40, 50] | [60, 160] | [80, 95] | [70, 85] | [80, 90] |
| x3 | [100, 120] | [50, 70] | [25, 30] | [50, 70] | [30, 40] | [55, 65] | [30, 45] | [20, 50] | [75, 80] |
| x4 | [110, 125] | [65, 85] | [30, 50] | [60, 80] | [40, 45] | [60, 70] | [55, 75] | [50, 70] | [80, 90] |
| x5 | [135, 150] | [95, 110] | [35, 45] | [100, 115] | [45, 55] | [95, 155] | [95, 110] | [85, 105] | [85, 90] |
| e12, x1 | [110, 145] | [100, 135] | [200, 280] | [105, 125] | [95, 115] | [300, 400] | [90, 115] | [80, 105] | [450, 550] |
| x2 | [110, 135] | [105, 120] | [300, 380] | [100, 120] | [95, 105] | [300, 400] | [85, 110] | [80, 100] | [450, 550] |
| x3 | [120, 150] | [100, 120] | [200, 250] | [110, 135] | [95, 115] | [300, 400] | [100, 110] | [85, 100] | [300, 400] |
| x4 | [100, 120] | [90, 110] | [350, 400] | [90, 100] | [80, 95] | [420, 500] | [80, 95] | [80, 90] | [600, 700] |
| x5 | [105, 130] | [95, 120] | [320, 400] | [90, 110] | [85, 100] | [350, 450] | [80, 100] | [80, 90] | [550, 600] |
计算过程为:
利用式(1)和式(2)将各决策成员的初始风险决策矩阵规范化(这里由于篇幅所致,就没有一一列举),对规范化后的矩阵利用式(3)~式(8)计算得到每个决策成员在不同状态下对不同方案的感知效用矩阵B=[bljit]p×m×n×z,如表 2所示,其中效用函数和后悔-欣喜函数中的系数α和δ采用文[27]中经实验验证的数据,分别取α=0.3和δ=1.88.
| 方案 | s1 | s2 | s3 | ||||||
| c1 | c2 | c3 | c1 | c2 | c3 | c1 | c2 | c3 | |
| e1,x1 | 0.536 9 | 0.545 1 | 0.915 5 | 0.646 4 | 0.738 1 | 1.000 0 | 0.898 6 | 0.799 3 | 0.977 1 |
| x2 | 0.557 7 | 0.617 7 | 0.946 4 | 0.742 9 | 0.826 8 | 0.856 7 | 0.979 9 | 0.930 6 | 0.981 7 |
| x3 | 0.571 5 | 0.639 2 | 0.992 4 | 0.750 8 | 0.826 7 | 0.987 1 | 0.949 6 | 0.870 3 | 0.995 4 |
| x4 | 0.509 3 | 0.596 0 | 0.954 1 | 0.654 5 | 0.738 2 | 0.974 2 | 0.909 0 | 0.860 3 | 0.981 7 |
| x5 | 0.467 3 | 0.567 0 | 0.954 1 | 0.605 6 | 0.693 4 | 0.987 1 | 0.827 0 | 0.789 2 | 0.997 1 |
| e2,x1 | -0.117 3 | -0.740 4 | 0.923 3 | -0.002 7 | 0.038 5 | 0.948 4 | 0.047 3 | -0.139 8 | 0.926 3 |
| x2 | -0.121 7 | -0.073 9 | 0.923 2 | -0.007 6 | 0.027 7 | 0.935 4 | 0.047 3 | -0.174 3 | 0.903 1 |
| x3 | -0.126 0 | -0.078 4 | 0.938 6 | -0.007 6 | 0.016 9 | 0.935 4 | 0.022 0 | -0.126 2 | 0.931 0 |
| x4 | -0.130 4 | -0.087 4 | 0.954 0 | -0.017 4 | 0.016 9 | 0.928 9 | 0.015 7 | -0.099 4 | 0.940 2 |
| x5 | -0.139 1 | -0.096 4 | 0.938 6 | -0.027 3 | -0.004 9 | 0.935 4 | 0.009 3 | -0.188 2 | 0.931 0 |
| e3,x1 | -0.323 7 | -0.310 5 | 0.923 6 | -0.209 5 | -0.213 7 | 0.954 8 | -0.157 3 | -0.217 0 | 0.981 7 |
| x2 | -0.240 0 | -0.214 2 | 0.931 0 | -0.187 4 | -0.164 5 | 0.987 1 | -0.143 4 | -0.216 9 | 0.986 3 |
| x3 | -0.225 6 | -0.146 9 | 0.946 4 | -0.187 4 | -0.146 6 | 0.987 1 | -0.136 7 | -0.167 1 | 0.981 7 |
| x4 | -0.202 1 | -0.132 9 | 0.977 1 | -0.160 4 | -0.111 5 | 0.974 2 | -0.155 8 | -0.153 3 | 0.995 4 |
| x5 | -0.192 9 | -0.128 3 | 0.938 7 | -0.128 6 | -0.129 0 | 0.941 9 | -0.102 2 | -0.092 7 | 0.995 4 |
| e4,x1 | 0.839 0 | 0.794 6 | -0.223 5 | 0.806 3 | 0.913 9 | 0.103 1 | 0.898 6 | 0.696 3 | -0.012 7 |
| x2 | 0.740 2 | 0.794 6 | -0.118 0 | 0.806 3 | 0.870 6 | 0.103 1 | 0.949 6 | 0.900 4 | -0.014 7 |
| x3 | 0.806 2 | 0.863 8 | 0.175 6 | 0.884 5 | 0.884 5 | 0.103 1 | 0.847 6 | 0.850 2 | -0.012 7 |
| x4 | 0.673 3 | 0.689 2 | -0.118 0 | 0.798 4 | 0.798 4 | -0.150 2 | 0.795 7 | 0.612 7 | -0.012 7 |
| x5 | 0.706 9 | 0.759 7 | -0.223 5 | 0.845 4 | 0.870 6 | -0.241 1 | 0.898 6 | 0.747 8 | -0.147 2 |
| | |||||||||
| e9,x1 | 0.059 8 | 0.130 1 | 0.829 9 | 0.148 5 | 0.199 7 | 0.896 3 | 0.022 0 | -0.021 4 | 0.898 3 |
| x2 | 0.055 8 | 0.117 8 | 0.798 4 | 0.139 3 | 0.173 4 | 0.870 1 | 0.015 6 | -0.008 7 | 0.912 4 |
| x3 | 0.075 6 | 0.138 2 | 0.829 9 | 0.166 8 | 0.244 9 | 0.919 5 | 0.053 5 | 0.022 7 | 0.940 2 |
| x4 | 0.031 9 | 0.105 5 | 0.702 9 | 0.106 8 | 0.117 6 | 0.777 4 | -0.022 9 | -0.055 9 | 0.870 5 |
| x5 | 0.043 9 | 0.109 6 | 0.766 7 | 0.134 7 | 0.128 0 | 0.856 9 | -0.016 4 | -0.047 0 | 0.889 2 |
| e10,x1 | 0.839 0 | 0.796 4 | -0.223 5 | 0.806 3 | 0.913 9 | 0.103 1 | 0.898 6 | 0.696 3 | -0.138 4 |
| x2 | 0.936 0 | 0.932 3 | 0.353 2 | 0.961 7 | 0.957 1 | 0.256 7 | 0.949 6 | 0.900 4 | 0.102 0 |
| x3 | 0.806 2 | 0.868 3 | 0.175 6 | 0.884 5 | 0.913 9 | 0.103 1 | 0.847 5 | 0.850 2 | -0.012 7 |
| x4 | 0.838 8 | 0.829 2 | 0.175 6 | 0.837 6 | 0.782 7 | 0.103 1 | 0.795 7 | 0.748 2 | 0.044 8 |
| x5 | 0.806 2 | 0.829 2 | -0.118 0 | 0.884 5 | 0.807 6 | -0.241 1 | 0.949 2 | 0.747 8 | -0.201 6 |
| e11,x1 | -0.249 6 | -0.204 3 | 0.915 5 | -0.160 4 | -0.279 1 | 0.770 8 | -0.082 0 | -0.106 0 | 0.977 1 |
| x2 | -0.284 8 | -0.265 4 | 0.946 4 | -0.243 8 | -0.300 4 | 0.856 6 | -0.164 3 | -0.167 1 | 0.981 7 |
| x3 | -0.323 7 | -0.322 3 | 0.992 4 | -0.319 1 | -0.331 4 | 0.987 1 | -0.319 5 | -0.294 8 | 0.995 4 |
| x4 | -0.306 2 | -0.287 1 | 0.954 1 | -0.292 3 | -0.307 7 | 0.974 2 | -0.229 9 | -0.217 0 | 0.981 7 |
| x5 | -0.254 5 | -0.229 1 | 0.954 1 | -0.204 0 | -0.286 1 | 0.770 8 | -0.122 6 | -0.119 3 | 0.977 1 |
| e12,x1 | -0.285 2 | -0.199 5 | 0.300 4 | -0.187 4 | -0.146 7 | 0.180 1 | -0.122 7 | -0.126 1 | 0.157 2 |
| x2 | -0.295 6 | -0.209 2 | -0.074 4 | -0.198 4 | -0.158 5 | 0.180 1 | -0.136 5 | -0.132 8 | 0.157 2 |
| x3 | -0.269 7 | -0.214 2 | 0.353 2 | -0.171 2 | -0.146 7 | 0.180 1 | -0.115 8 | -0.126 0 | 0.472 7 |
| x4 | -0.323 7 | -0.234 2 | -0.223 5 | -0.232 2 | -0.188 8 | -0.185 6 | -0.164 3 | -0.146 4 | -0.201 6 |
| x5 | -0.306 5 | -0.219 2 | -0.159 1 | -0.220 8 | -0.176 6 | 0.021 9 | -0.157 3 | -0.146 4 | -0.012 7 |
在此基础上,对决策成员的感知效用矩阵按属性权重进行集结,采用聚类算法对集结后的各决策成员矩阵进行聚类,取阈值γ=0.9[28],得到聚集数为K=4、聚集矩阵Gk=[glt]n×z和聚集初始权重 wCk=[0.750 0,0.083 3,0.083 3,0.083 3]T,k=1,2,3,4,结果如表 3所示.
| 聚集 | 成员数 | 成员 | 聚集矩阵 | |||
| Ck | nk | ei | c1 | c2 | c3 | |
| C1 | 6 | e2,e3,e6,e7,e9,e11 | x1 | -0.002 6 | -0.040 7 | 0.905 3 |
| x2 | -0.002 4 | -0.052 1 | 0.914 6 | |||
| x3 | -0.005 9 | -0.048 7 | 0.933 1 | |||
| x4 | -0.066 3 | -0.080 7 | 0.906 4 | |||
| x5 | -0.059 4 | -0.110 3 | 0.894 1 | |||
| C2 | 2 | e4,e10 | x1 | 0.837 8 | 0.822 7 | -0.063 2 |
| x2 | 0.878 8 | 0.891 0 | 0.127 7 | |||
| x3 | 0.845 8 | 0.881 1 | 0.109 0 | |||
| x4 | 0.788 8 | 0.752 8 | 0.005 3 | |||
| x5 | 0.833 4 | 0.815 3 | -0.199 6 | |||
| Ck | nk | ei | c1 | c2 | c3 | |
| C3 | 2 | e5,e12 | x1 | -0.226 9 | -0.175 0 | 0.083 1 |
| x2 | -0.224 9 | -0.173 7 | 0.073 7 | |||
| x3 | -0.206 5 | -0.166 6 | 0.265 7 | |||
| x4 | -0.104 6 | -0.098 2 | 0.354 1 | |||
| x5 | -0.248 8 | -0.192 0 | -0.130 7 | |||
| C4 | 2 | e1,e8 | x1 | 0.524 3 | 0.559 2 | 0.961 6 |
| x2 | 0.568 1 | 0.612 0 | 0.952 2 | |||
| x3 | 0.553 4 | 0.601 7 | 0.973 1 | |||
| x4 | 0.511 3 | 0.564 8 | 0.966 2 | |||
| x5 | 0.500 6 | 0.555 5 | 0.978 1 | |||
利用式(11)计算得到决策成员的初始权重ωi1,并利用式(13)~式(17)计算决策成员的修正权重ωi2,从而求得各决策成员修正后的综合权重ωi,如表 4所示.
| 权重 | e1 | e2 | e3 | e4 | e5 | e6 | e7 | e8 | e9 | e10 | e11 | e12 |
| wi1 | 0.083 3 | 0.750 0 | 0.750 0 | 0.083 3 | 0.083 3 | 0.750 0 | 0.750 0 | 0.083 3 | 0.750 0 | 0.083 3 | 0.750 0 | 0.083 3 |
| wi2 | 0.500 0 | 0.180 5 | 0.164 8 | 0.500 0 | 0.500 0 | 0.166 0 | 0.168 8 | 0.500 0 | 0.163 1 | 0.500 0 | 0.156 9 | 0.500 0 |
| wi | 0.041 7 | 0.135 4 | 0.123 6 | 0.041 7 | 0.041 7 | 0.124 5 | 0.126 6 | 0.041 7 | 0.122 3 | 0.041 7 | 0.117 6 | 0.041 7 |
利用式(18)~式(22)计算同一聚集内部决策成员偏好与其所在偏好聚集的冲突风险熵,从而由式(23)得到决策成员ei关于方案xl的冲突风险权重hli,如表 5所示.
| 权重 | e1 | e2 | e3 | e4 | e5 | e6 | e7 | e8 | e9 | e10 | e11 | e12 |
| h1 | 0.200 5 | 0.149 8 | 0.152 8 | 0.098 4 | 0.153 3 | 0.161 6 | 0.150 0 | 0.200 5 | 0.158 1 | 0.098 4 | 0.156 9 | 0.153 3 |
| h2 | 0.196 0 | 0.273 6 | 0.271 2 | 0.192 5 | 0.273 3 | 0.270 9 | 0.273 4 | 0.196 0 | 0.266 6 | 0.192 5 | 0.266 1 | 0.273 3 |
| h3 | 0.202 5 | 0.273 6 | 0.271 2 | 0.327 0 | 0.273 3 | 0.270 9 | 0.273 4 | 0.202 5 | 0.266 6 | 0.327 0 | 0.266 1 | 0.273 3 |
| h4 | 0.199 1 | 0.139 7 | 0.158 8 | 0.185 8 | 0.154 5 | 0.158 7 | 0.159 2 | 0.199 1 | 0.154 7 | 0.185 8 | 0.151 3 | 0.154 5 |
| h5 | 0.201 8 | 0.163 3 | 0.146 0 | 0.196 3 | 0.145 7 | 0.137 8 | 0.144 0 | 0.201 8 | 0.154 1 | 0.196 3 | 0.159 6 | 0.145 7 |
由求得的Gk、ωi和hli利用式(24)计算方案的排序向量O =[0.043 9,0.070 7,0.080 5,0.045 3,0.040 7]T,由此得到5个方案的排序结果x3>x2>x4>x1>x5,即方案3为最优方案.
为了验证参数对决策结果的影响,这里对风险规避系数δ取不同的值计算排序向量,结果如表 6所示.
| δ | 排序结果 |
| δ=0.1 | x3>x1>x2>x4>x5 |
| δ=0.5 | x3>x4>x2>x1>x5 |
| δ=1.0 | x3>x4>x2>x1>x5 |
| δ=1.5 | x3>x2>x4>x1>x5 |
| δ=2.0 | x3>x2>x4>x1>x5 |
由表 6可知,参数δ取值不同,排序结果也发生相应的变化,但最优排序方案都为x3.
为了进一步说明本文所提方法的有效性,这里分别采用不考虑决策成员后悔规避的常规排序方法和基于前景理论的风险型多属性决策方法对本文算例进行排序,运用式(1)~式(2)对初始风险型决策矩阵规范化,然后对规范化矩阵进行聚类,为了不失一般性,3种方法同样得到4个聚类,即K=4和聚集权重wCk=[0.042 6,0.095 7,0.383 0,0.383 0]T,前者取阈值γ=0.7,方案的偏好集结{x1,x2,x3,x4,x5},其中,x1∈[0.087 9,0.168 3],x2∈ [0.160 2,0.239 2],x3∈[0.176 8,0.256 8],x4∈[0.120 4,0.202 0],x5∈[0.066 4,0.135 4].在此基础上,根据区间数计算法则和可能度公式对方案进行排序:x3>x2>x1>x4>x5.后者取阈值γ=0.87,方案的前景排序向量[x3>x2>x4>x1>x5]=[0.405 3,0.688 5,0.785 2,0.670 4,0.648 3],排序结果为x3>x2>x4>x5>x1.
可以看出,依据本文所提出的方法与不考虑决策成员后悔规避的常规排序方法和基于前景理论的决策方法确定的决策最优方案是一致的,但3种方法聚类时的阈值是不同的(分别为0.9、0.7和0.87).这是因为,在贴合实际情况下考虑决策成员对损失及收益的敏感程度不同的心理行为,使得决策成员对各方案的感知效用偏好相近,一致性程度高;从排序结果可以看出,本文所提方法的结果与基于情景理论决策方法的结果更接近,分别考虑后悔规避和损失规避使得方案4的感知效用值和前景值都要高于方案1;且与基于情景理论的决策方法相比,本文所提方法对决策成员权重进行修正和考虑聚集内部成员的冲突风险熵后,使得成员权重更能反映决策成员在决策过程中所做贡献的大小,方案1的冲突风险熵低于方案5,排序结果符合决策成员的初始偏好信息,避免了由冲突风险造成的决策信息失真.
3 结论本文针对决策成员权重未知且决策信息为区间数的风险应急决策问题,提出一种基于冲突风险熵和后悔规避的大群体决策方法.该方法的特点是从决策成员的主观心理感知和决策信息的客观完整性两个方面来降低决策风险.首先在决策过程中考虑决策成员对风险规避的敏感程度,引入后悔理论得到决策成员的综合感知效用值,更加贴近决策实际、更为决策成员所接受.进而计算决策成员的初始权重并从相似度角度对权重进行修正,更能反映决策成员所做的贡献,提高决策的一致性程度.同时从冲突水平和状态结果发生的概率两方面来测度风险的大小,保证决策信息更客观、更科学,降低由不可避免地决策冲突造成的决策信息失真风险.在决策过程中,尽管聚集之间的冲突可以通过冲突消解降低但却无法消除,由聚集冲突带来的风险也一直存在,因此如何测度聚集之间的冲突风险还有待进一步的研究.
| [1] | Yue E, Zhu Y P. Study on emergency decision-making of natural disaster based on collaboration of multi-agent[J]. Applied Mechanics & Materials, 2013, 411(411-414): 2684–2693. |
| [2] |
徐选华, 钟香玉, 陈莹, 等.
基于一致性与共识的工程机械知识产权产品推荐群决策方法[J]. 信息与控制, 2016, 45(2): 235–240.
Xu X H, Zhong X Y, Chen Y, et al. A group decision making method for construction machinery intellectual property products recommendation based on consistency and consensus[J]. Information and Control, 2016, 45(2): 235–240. |
| [3] |
袁媛, 刘洋, 樊治平.
考虑后悔规避的突发事件应急响应的风险决策方法[J]. 系统工程理论与实践, 2015, 35(10): 2630–2636.
Yu an, Liu Y, Fan Z P. Risk decision making method for emergency response considering regret aversion[J]. System Engineering Theory and Practice, 2015, 35(10): 2630–2636. DOI:10.12011/1000-6788(2015)10-2630 |
| [4] |
王亮, 王应明.
基于前景理论的动态参考点应急决策方法研究[J]. 中国管理科学, 2013, 21(S1): 132–140.
Wang L, Wang Y M. Study on the emergency decision method of dynamic reference point based on prospect theory[J]. Chinese Journal of Management Science, 2013, 21(S1): 132–140. |
| [5] | Liu Y, Fan Z P, Zhang Y. Risk decision analysis in emergency response:A method based on cumulative prospect theory[J]. Computers & Operations Research, 2014, 42(2): 75–82. |
| [6] |
程铁军, 吴凤平, 李锦波.
基于累积前景理论的不完全信息下应急风险决策模型[J]. 系统工程, 2014, 32(4): 70–75.
Chen T J, Wu F P, Li J B. Risk decision model for emergency response based on cumulative prospect theory with incomplete information[J]. Systems Engineering, 2014, 32(4): 70–75. |
| [7] |
陈业华, 王浩, 宋之杰.
基于效用风险熵的突发事件应急方案动态调整[J]. 系统工程与电子技术, 2016, 38(9): 2093–2098.
Chen Y H, Wang H, Song Z J. Dynamic adjustment for emergency decision-making based on utility risk entropy[J]. Systems Engineering and Electronics, 2016, 38(9): 2093–2098. DOI:10.3969/j.issn.1001-506X.2016.09.18 |
| [8] | Xu X H, Liang D, Chen X Y H. A risk elimination coordination method for large group decision-making in natural disaster emergencies[J]. Human & Ecological Risk Assessment, 2015, 21(5): 1314–1325. |
| [9] | Liu Y, Fan Z P, Yuan Y, et al. A FTA-based method for risk decision-making in emergency response[J]. Computers & Operations Research, 2011, 42(2): 608–612. |
| [10] | Zhou J L, Shia Y B, Sun Z Y. A hybrid fuzzy FTA-AHP method for risk decision-making in accident emergency response of work system[J]. Journal of Intelligent & Fuzzy Systems, 2015, 29(4): 1381–1393. |
| [11] |
谢非, 杨茜, 黄晓娟.
基于解释结构模型的企业汇率风险应急机制构建研究[J]. 重庆大学学报:社会科学版, 2015, 21(4): 59–64.
Xie F, Yang Q, Huang X J. Study on constructing emergency mechanism system of enterprises exchange rate risk based on interpretative structural model[J]. Journal of Chongqing University:Social Science Edition, 2015, 21(4): 59–64. |
| [12] |
江时雨, 陈建宏, 李涛, 等.
基于Bayes-Monte Carlo的突发事件应急方案风险决策方法研究[J]. 世界科技研究与发展, 2015, 31(1): 5–8.
Jiang S Y, Chen J H, Li T, et al. Researches on risk decision-making method of emergencies contingency plans based on Bayes-Monte Carlo[J]. World Sci-tech R & D, 2015, 31(1): 5–8. |
| [13] | Dillon R L, Liebe R M, Bestafka T. Risk-based decision making for terrorism applications[J]. Risk Analysis, 2009, 29(3): 321–335. DOI:10.1111/risk.2009.29.issue-3 |
| [14] | Sun B, Ma W, Chen X. Fuzzy rough set on probabilistic approximation space over two universes and its application to emergency decision-making[J]. Expert Systems, 2015, 32(4): 507–521. DOI:10.1111/exsy.v32.4 |
| [15] | Xu X H, Du Z J, Chen X H. Consensus model for multi-criteria large-group emergency decision making considering non-cooperative behaviors and minority opinions[J]. Decision Support Systems, 2015, 79(C): 150–160. |
| [16] | Xu X H, Zhong X Y, Chen X H, et al. A dynamical consensus method based on exit-delegation mechanism for large group emergency decision making[J]. Knowledge-Based Systems, 2015, 86(C): 237–249. |
| [17] | Kahneman D, Tversky A. Prospect theory:An analysis of decision under risk[J]. Econometrica, 1797, 47(2): 263–291. |
| [18] | Liu B, Shen Y, Chen Y, et al. A two-layer weight determination method for complex multi-attribute large-group decision-making experts in a linguistic environment[J]. Information Fusion, 2015, 23(C): 156–165. |
| [19] | Xu X H, Chen X H. Research of a kind of method of multi-attributes and multi-schemes large group decision making[J]. Journal of Systems Engineering, 2008, 23(2): 137–141. |
| [20] | Xu X, Wang B, Zhou Y. A method based on trust model for large group decision-making with incomplete preference information[J]. Journal of Intelligent & Fuzzy Systems, 2016, 30(6): 3551–3565. |
| [21] |
姜丹, 钱玉美.
效用风险熵[J]. 中国科学技术大学学报, 1994, 24(4): 461–469.
Jiang D, Qian Y M. Effect risk entropy[J]. Journal of China University of Science and Technology, 1994, 24(4): 461–469. |
| [22] | Bell D E. Regret in decision making under uncertainty[J]. Operations Research, 1982, 30(5): 961–981. DOI:10.1287/opre.30.5.961 |
| [23] | Loomes G, Sugden R. Regret Theory:An alternative theory of rational choice under uncertainty[J]. Economic Journal, 1982, 92(368): 805–824. DOI:10.2307/2232669 |
| [24] | Tversky A, Kahneman D. Advances in prospect theory:Cumulative representation of uncertainty[J]. Journal of Risk & Uncertainty, 1992, 5(4): 297–323. |
| [25] |
张全, 樊治平, 潘德惠.
区间数多属性决策中一种带有可能度的排序方法[J]. 控制与决策, 1999, 14(6): 703–706.
Zhang Q, Fan Z P, Pan D H. A ranking approach with possibilities for multiple attribute decision making problems with intervals[J]. Control and Decision, 1999, 14(6): 703–706. |
| [26] |
徐选华, 陈晓红.
一种多属性多方案大群体决策方法研究[J]. 系统工程学报, 2008, 23(2): 137–141.
Xu X H, Chen X H. Research of a kind of method of multi-attributes and multi-schemes large group decision making[J]. Journal of Systems Engineering, 2008, 23(2): 137–141. |
| [27] |
张晓, 樊治平, 陈发动.
基于后悔理论的风险型多属性决策方法[J]. 系统工程理论与实践, 2013, 33(9): 2313–2320.
Zhang X, Fan Z P, Chen F D. Method for risky multiple attribute decision making based on regret theory[J]. System Engineering Theory and Practice, 2013, 33(9): 2313–2320. DOI:10.12011/1000-6788(2013)9-2313 |
| [28] |
徐选华.
面向特大自然灾害复杂大群体决策模型及应用[M]. 北京: 科学出版社, 2012: 23-29.
Xu X H. Complex large group decision making models and its application oriented outsize nature disasters[M]. Beijing: Science Press, 2012: 23-29. |



