0 引言
随着工业化进程的不断加快,城市污水处理的重要性也越来越高[1].在污水处理过程中,化学需氧量(chemical oxygen demand,COD)是衡量水中有机物质含量的重要指标,五日生物需氧量(five-day biochemical oxygen demand,BOD5)的数值可直接反映水体中可被生物降解的污染物的含量,因此及时测定COD、BOD5对水质污染防治和监测具有十分关键的作用.由于污水处理系统的工艺复杂,影响重要出水参数测量的因素众多,传统的COD、BOD5测量方法往往难以满足精确、环保、经济和实时性等要求,因此建立高质量的污水软测量模型非常必要[2].除此之外,在污水处理现场,随着新数据和新特征的不断出现,根据历史数据离线建立的软测量模型的测量效果会变差,为了保证软测量模型能够跟随新数据及时进行更新,必须研究测量精度高且计算速度快的在线软测量模型.
污水处理系统的关键在出水水质的软测量方面,很多学者进行了研究.在离线软测量建模中,任东红利用改进的粒子群算法对集成神经网络进行训练,建立集成前馈神经网络的污水软测量模型[3].乔俊飞等采用自组织随机权神经网络和基于粒子群优化的回声状态神经网络对污水处理指标BOD5进行软测量建模[4-5].文[6-7]通过利用遗传优化算法和BP神经网络进行建模,实现对5日生物需氧量BOD5的预测.宋贤民等使用SVM进行污水处理的出水水质的参数预测[8],徐方舟利用基于粒子群的LSSVM算法对污水处理系统出水数据进行软测量[9],张杰等将联合支持向量机和神经网络的方法用于SBR污水处理中COD的软测量[10].在线软测量建模方面,张昭昭等利用在线减法聚类算法将实时工况数据样本进行划分,动态集成各子模型的输出,对污水处理过程出水的氨氮含量进行预测[11].丛秋梅等[12-13]提出由简化机理模型和建模误差补偿模型组成的同步聚类出水COD混合在线软测量方法,还将小波神经网络模型与稳定学习算法相结合,提出了一种基于稳定Hammerstein模型(H模型)的COD在线软测量建模方法.
分析上述研究现状,神经网络模型对训练样本依赖性较强,在训练过程中容易陷入局部最优,泛化能力有待提高.与神经网络相比,支持向量机具有全局最优解,泛化能力更强,但它的核函数必须满足Mercer条件且对惩罚参数敏感[14-15],另外由于支持向量机的稀疏性会随着训练样本数量的增加而降低,随着训练集的增大模型计算量会变大,在线建模时快速性难以满足实时性要求.快速相关向量机(FAST relevance vector machine,FASTRVM)是一种在贝叶斯框架下的稀疏概率模型[16],泛化能力强,另外该算法利用快速边际似然法可以提高模型的学习速度.本文作者采用单一高斯核函数的FASTRVM建立了污水出水水质BOD5的在线软测量模型,获得了较好的预测精度,并验证了该方法的有效性[17].但是进一步研究发现,单一高斯核函数缺乏灵活性,对复杂映射关系的描述能力不佳,因此针对污水处理实变过程中在线检测对于准确性与实时性的要求,本文提出了一种多属性核函数快速相关向量机(multi-attributes Gaussian kernel function FAST relevance vector machine,MAG-FASTRVM)的在线污水软测量模型来解决污水处理厂重要参数的测量建模问题.该模型使用多属性核函数构造贝叶斯框架的相关向量机来在线预测输出指标,并利用快速边际似然算法来加快更新模型的速度,实现对污水参数的实时在线测量.与支持向量机、相关向量机、单一核函数快速相关向量机及几种基于不同核函数的多核函数快速相关向量机算法进行对比可知,MAG-FASTRVM模型在保证检测精度的前提下可显著减少建模训练时间.
1 在线污水软测量模型的建立 1.1 MAG-FASTRVM的基本模型给定一组输入数据xn及其输出的目标值tn,有D={xn,tn}n=1N,xn∈RM,假设输出目标值的函数为
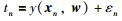
|
(1) |
式中,εn为服从(0,σ2)的高斯分布且相互独立的附加噪声;模型权值w=[w0,w1,…,wN]T为N+1维列向量,由模型权值wi组成;y(xn,w)由核函数k(x,xi)的加权模型表示:
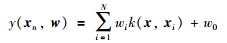
|
(2) |
核函数在一定程度上对RVM的学习性能造成影响.选择的核函数不同,RVM的预测能力也会存在差异.为避免过学习和过适应问题,改善RVM的学习能力,选择多属性高斯核函数作为RVM的核函数:
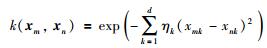
|
(3) |
多属性核函数的参数可表示为η=[η1,η2,…,ηd],其中d是输入向量中属性的个数.实际上它正是高斯核半径平方的倒数.称ηk为第k(k=1,2,…,d)个核参数,xmk、xnk分别表示对应第m、n个样本的第k个输入特征.多属性高斯核函数在各个属性使用不同的核参数.
定义输入数据集的输出t=[t1,t2,…,tN]T为N维列向量且tn服从独立分布,输入数据集的似然估计概率为
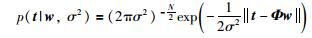
|
(4) |
称Φ为贝叶斯矩阵,有:
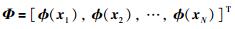
|
(5) |
由于ϕ(xn)=[1,k(xn,x1),k(xn,x2),…,k(xn,xN)]T是(N+1)×1维矩阵,所以Φ是N×(N+1)维矩阵.下文公式中的贝叶斯矩阵Φ即为多属性高斯核函数构成的贝叶斯矩阵.
在参数估计过程中模型的权值参数wi的个数会不断增加,从而导致过度学习现象的发生.在SVM中为了避免模型的过度学习问题,常常会给参数设定一些限制条件.实验证明这种处理方法非常有效[18-20].由于RVM是基于贝叶斯框架的概率模型,因此也可以限制权值服从高斯分布且相互独立的概率函数来简化模型学习的复杂度.权值限制条件形式为
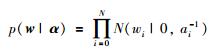
|
(6) |
α=[α0,α1,…,αN]是N+1维的超参数向量,决定了权值w的先验分布并对模型稀疏性有着间接的影响.大部分超参数αi的取值会在模型学习的过程中逐渐趋向于无穷.使趋向于无穷的αi对应的权值参数wi取值为0可以使模型获得可观的稀疏性.
由D给定模型观测数据集输出t,令β=σ-2,通过对超参数α、β和权值w积分得到预测样本t*的分布:
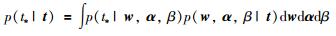
|
(7) |
可推知:
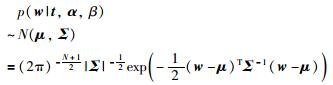
|
(8) |
其协方差有:
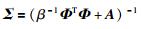
|
(9) |
其中矩阵A是以超参数αi为对角元素的对角矩阵.后验均值矩阵μ有:
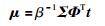
|
(10) |
α、β的边缘似然分布为
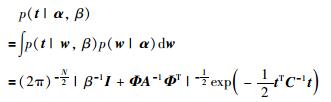
|
(11) |
其中,矩阵C=β-1I+ΦA-1ΦT.对式(11)取对数有:
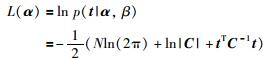
|
(12) |
通过最大化L(α)可以实现对超参数进行估计.为了快速求取超参数,得到稀疏性模型,使用快速边际似然算法.与常规RVM通过稀疏性学习自上而下将M个初始基函数逐渐减少至相关向量的个数来确定贝叶斯矩阵的方法不同,该算法采用自下而上的基函数选择方法对相关向量机模型的超参数进行快速估计.快速边际似然算法[21-22]将L(α)中的矩阵C进行分解成2个部分:一部分为只与αi有关,另一部分是消去基函数ϕi后的边缘似然函数.矩阵C分解形式为
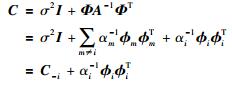
|
(13) |
其中,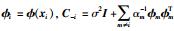
当qi2>si时,L(α)对αi的2阶偏导数是恒小于0的.这时L(α)有唯一最大值点.易求得此时αi= si2 qi2-si;当qi2≤si时,将超参数αi置为无限大,并去除相应的基向量ϕi.
综上所述,MAG-FASTRVM模型的建模步骤为:
1) 初始化核参数及初始噪声方差σ2,建立由多属性高斯核函数组成的贝叶斯矩阵Φ,获得初始基向量ϕi.
2) 设置与初始基向量无关的超参数αm(m≠i)为无穷大,结合ϕi,由式(14)计算与初始基向量对应的超参数αi:
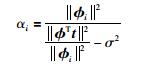
|
(14) |
3) 根据式(9)计算协方差矩阵Σ,并通过式(10)得到后验权值矩阵μ.
4) 初始化所有基函数ϕm对应的稀疏因子sm及质量因子qm,并计算N个候选基向量ϕi对应的θi=qi2-si,θi的值决定了超参数αi是否进行更新.
5) 将θi与0作比较.如θi>0,αi < ∞且候选基向量ϕi在模型中,则更新超参数αi;如θi>0,αi=∞但候选基向量ϕi不在模型中,则将候选基向量ϕi添加到模型中并更新超参数αi;若θi≤0且αi < ∞,则删除基向量ϕi并设置超参数αi=∞.
6) 按式(15)更新噪声方差σ2:
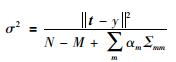
|
(15) |
其中,y是模型输入测试样本后得到的输出值,N为输入样本个数,M为基函数的个数.
7) 更新sm和qm,重新迭代计算协方差矩阵Σ和后验权值矩阵μ.如超参数值收敛或者达到最大迭代次数,则终止迭代,否则转到步骤4).
8) 输出最终权值矩阵μ、噪声方差σ2和相关向量个数.
1.2 MAG-FASTRVM在线软测量模型至此,本文研究的MAG-FASTRVM模型是基于相关向量机的离线模型.这种模型建立后经过学习一般不会再发生变化.但是在实际应用中由于进水水质、水量、操作条件等因素往往会出现变化,如果只采用固定历史数据建模来进行预测,可能使得预测结果与实际情况有偏差,从而难以准确地反映当前的污水状况.针对这一问题改进现有MAG-FASTRVM软测量模型[23],引入滚动时间窗方法对模型进行在线更新以实现对模型的在线校正.滚动时间窗是指数据流的一个子区间,它会随着时间进行变化.在学习过程中,通过子区间两端同时向同一个方向移动相同单位时间或相同数量的新数据,并忽略或删除与当前工况相距较大且相关性较小的旧数据.由于在这个过程中,数据是不断“滚动”变化的,故称这个不断变化的窗口为滚动时间窗.
加入了滚动时间窗的MAG-FASTRVM在线软测量模型步骤为:
1) 称一段连续的用于描述过去某段时间内系统状态的数据为长度为L的数据窗.将最早的一组长度为L的初始训练样本设为初始数据窗,用此数据窗建立初始MAG-FASTRVM模型.
2) 对最新得到的R组数据(xnew,ynew)进行预测,计算其预测偏差.
3) 用最新得到的R组数据(xnew,ynew)取代最早的R组数据,更新训练样本.
4) 利用更新后的训练样本重新建立MAG-FASTRVM模型,对目标参数进行预测.
5) 返回步骤2),直至测试完所有新得数据.
2 仿真实验与结果分析 2.1 实验辅助变量本文采用加州大学数据库(UCI)提供的污水数据进行仿真实验[24].该污水数据为城市污水处理厂用将近2年时间测得,涵盖了全年四季不同的气候情况,采样间隔0~2 d不等.数据集含527组38维样本.对污水数据进行去误差平滑、降维等预处理后,得到20维样本共400组.设BOD5、COD为输出变量,其余18个属性为输入变量.输入变量如表 1所示.
| 变量名 | 变量说明 |
| DBO-E | 输入生物需氧量 |
| DQO-E | 输入化学需氧量 |
| PH-D | 二级沉降器输入pH值 |
| DBO-D | 二级沉降器输入生物需氧量 |
| DQO-D | 二级沉降器输入化学需氧量 |
| SS-D | 输入沉淀物 |
| SED-D | 二级沉降器输入悬浮固体物 |
| PH-S | 输出pH值 |
| SS-S | 输出悬浮固体物 |
| SED-S | 输出沉淀物 |
| RD-DBO-P | 初沉池输入生物需氧量 |
| RD-SS-P | 初沉池输入悬浮固体物 |
| RD-DBO-S | 二沉池输入生物需氧量 |
| RD-DQO-S | 二沉池输入化学需氧量 |
| RD-DBO-G | 整个污水厂生物需氧量 |
| RD-DQO-G | 整个污水厂化学需氧量 |
| RD-SS-G | 整个污水厂悬浮固体浓度 |
| RD-SED-G | 整个污水厂可降解固体浓度 |
为了使污水处理厂能及时处理异常情况并加强对污水处理的运行控制,需要对出水水质进行及时的预测.仿真实验采用的计算机环境为:Intel Core处理器,4 GB内存,1 000 G硬盘.对原始数据集进行预处理后选取其中的400组数据.使用200组来进行模型训练,200组作为测试集来测试模型的精度.首先根据上文介绍的建模步骤建立MAG-FASTRVM的离线模型,分别与支持向量机(SVM)、相关向量机(RVM)及其它混合核函数下的快速相关向量机离线模型进行对比仿真实验.其它基于混合核函数的快速相关向量机包括:高斯核函数快速相关向量机(FASTRVM)多项式核函数相关向量机(MUPL-FASTRVM)及组合核函数快速相关向量机(C-FASTRVM).所有混合核函数下的快速相关向量机离线模型均采用遗传优化方法来进行参数优化.表 2、表 3是污水BOD5、COD在各模型下的预测结果,表中的运行时间等于模型每次在线更新的用时.
| 预测算法 | 均方根误差 | 相关向量个数/个 | 运行时间/s |
| SVM | 0.084 5 | 70 | 41.734 |
| RVM | 0.080 2 | 10 | 1.056 |
| FASTRVM | 0.069 0 | 12 | 0.493 |
| MUPL-FASTRVM | 0.080 5 | 14 | 0.518 |
| C-FASTRVM | 0.067 7 | 15 | 0.516 |
| MAG-FASTRVM | 0.047 3 | 4 | 0.472 |
| 预测算法 | 均方根误差 | 相关向量个数/个 | 运行时间/s |
| SVM | 0.085 6 | 82 | 65.352 |
| RVM | 0.113 6 | 28 | 1.343 |
| FASTRVM | 0.115 2 | 41 | 0.558 |
| MUPL-FASTRVM | 0.105 7 | 34 | 0.614 |
| C-FASTRVM | 0.101 3 | 38 | 0.602 |
| MAG-FASTRVM | 0.078 3 | 19 | 0.506 |
结合表 2、表 3中BOD5、COD的预测情况可见,相较于RVM、MAG-FASTRVM及其它基于混合核函数的FASTRVM,SVM的预测效果偏中等,但其模型的稀疏性、运行时间相对较差.结合模型的预测精度、模型稀疏性、运行时间等因素进行综合考量可判断,通过SVM达到适合的离线预测效果会存在较大的困难.
从稀疏性和运行时间来看,作为单核模型的RVM、FASTRVM及MUPL-FASTRVM与多核模型C-FASTRVM、MAG-FASTRVM表现相近.但C-FASTRVM、MAG-FASTRVM等多核模型的预测效果较其它单核模型相对较好.因此可判断多核模型比单核模型更适合对污水参数BOD5、COD进行离线学习.
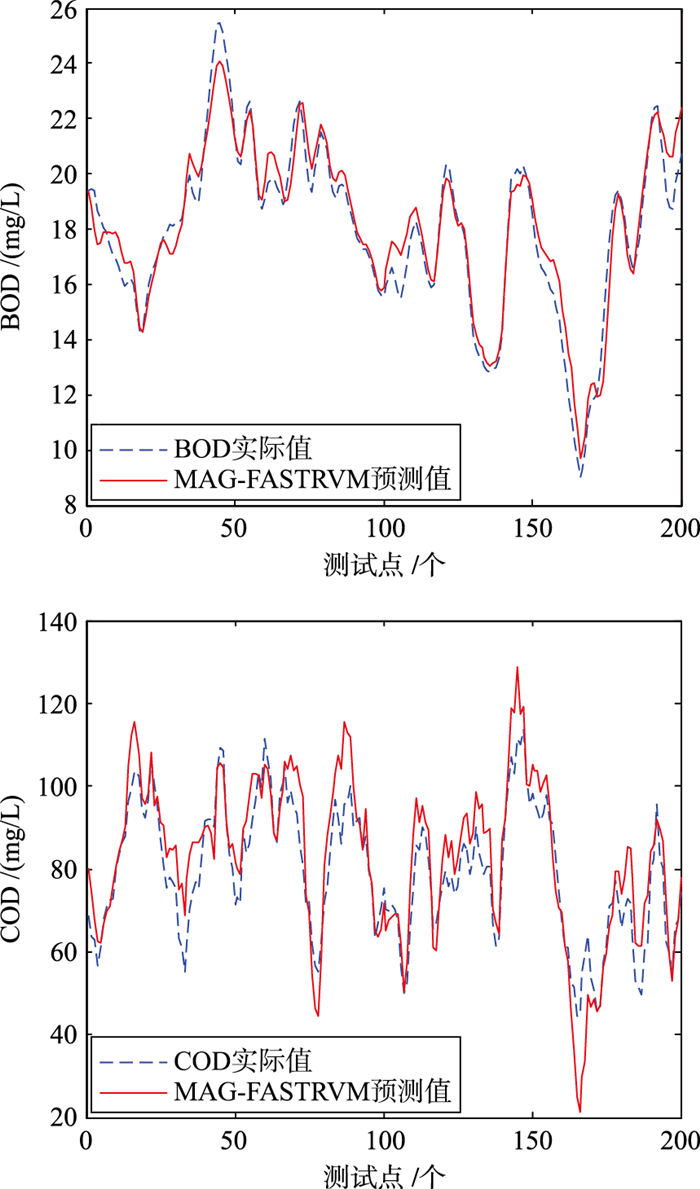
C-FASTRVM、MAG-FASTRVM都取得了较好的污水离线预测效果.通常,越稀疏的模型计算复杂度越低,其学习效率也会越高.而MAG-FASTRVM在模型的稀疏性和预测精度方面比C-FASTRVM表现更优.图 1是MAG-FASTRVM的BOD5、COD离线预测曲线.由图 1也可以看出,两个参数都会随时间的变化而变化,其中BOD5变化较小而COD变化的幅度相对较大.图 2、图 3分别对比了MAG-FASTRVM和其它几种模型进行BOD5、COD预测时在每个测试点处预测误差的绝对值.
|
| 图 1 MAG-FASTRVM模型的BOD5、COD离线预测图 Figure 1 BOD5, COD offline forecast chart of the MAG-FASTRVM model |
|
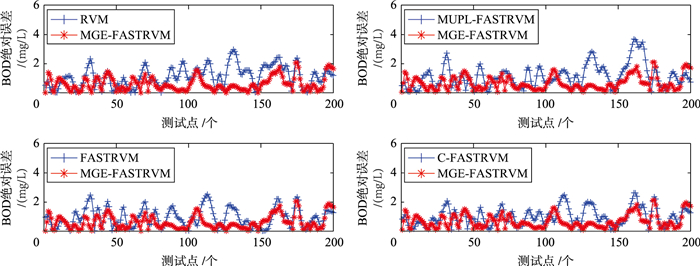
| 图 2 BOD5预测误差绝对值对比曲线 Figure 2 Contrast curves of the absolute values of the BOD5 prediction errors |
|
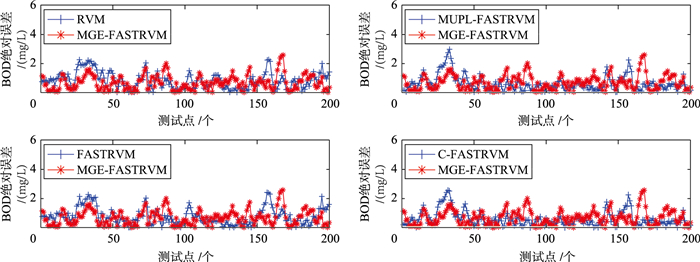
| 图 3 COD预测误差绝对值对比曲线 Figure 3 Contrast curves of the absolute values of the COD prediction errors |
BOD5的工况变化较小,这使得模型容易对BOD5达到令人满意的预测效果.从图 2可以看出,所有模型对BOD5的预测误差都相对较低.整体上MAG-FASTRVM对BOD5的预测效果较其它模型好且在BOD5预测时在大多数工况点的预测误差都要低于其它模型,这表明MAG-FASTRVM对BOD5的工况变化有着良好的适应性.由图 2、图 3可知,与BOD5预测相比所有模型在对COD进行预测时预测效果都稍差,这是因为相较于BOD5,COD自身工况变化较大.由图 3可知,在[20, 40]、[80, 100]及[140, 160]区间的工况点附近模型输出与实际情况偏差较大.这时MAG-FASTRVM对处于测试点的跟踪能力下降,其预测效果还不如其它模型.由此可知,虽然在多数情况下模型的预测都较接近实际值,但仍然存在采样预测效果不甚理想的区间,这说明离线模型并不能一直有效预测并且适应出水的变化.
2.3 MAG-FASTRVM的在线污水仿真实验进行污水处理时,平均间隔1 d采集一个数据.由于更新数据的频率不高,数量也不多,因此可以按照数据的采集频率进行短期学习来更新现有模型.采集得到的污水数据是一种时序序列,设置滚动时间窗的长度为200.这样在线模型与离线模型一样,会选择200组连续数据作为训练数据.但与离线模型直接用剩下的200组数据作为测试集不同,在线校正模型将剩下的200组数据作为新数据依时序加入到模型中.模型进行学习时,每当更新一个新的数据,滚动窗口便向前移动一个单位,使更新数据加入到训练数据中,同时删除一个最早的数据.这样在训练集样本数目不变的情况下可以保证每次的训练数据包含新的信息且避免历史所含数据被新数据包含的信息淹没,从而提高模型对不同工况点的适应性.
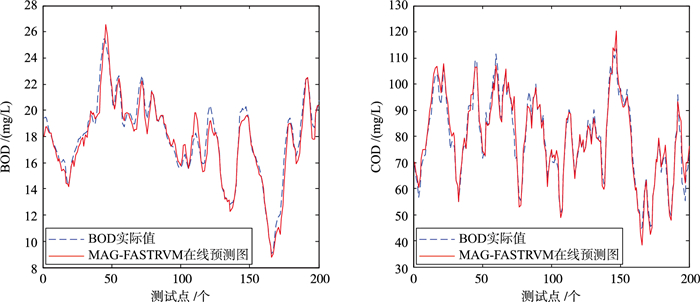
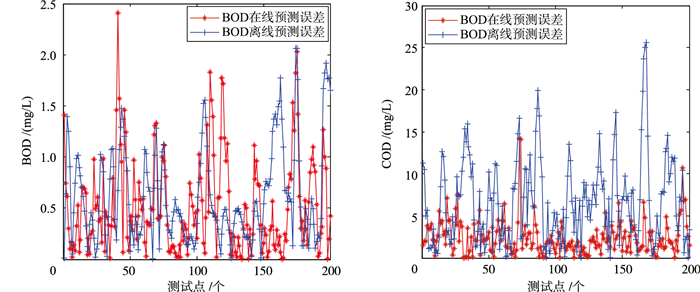
设置时间滚动窗长度L=200,移动长度R=1,使用200组历史数据建立初始模型,剩下200组数据充当更新数据,根据上文介绍的MAG-FASTRVM在线建模方法建立在线软测量模型,并对出水水质BOD5、COD浓度的输出进行实时预测.图 4是MAG-FASTRVM模型的在线预测图,图 5是MAG-FASTRVM离线模型和在线模型预测误差绝对值的对比图.
|
| 图 4 MAG-FASTRVM模型的在线预测图 Figure 4 Online forecast chart of the MAG-FASTRVM model |
|
| 图 5 MAG-FASTRVM离线和在线预测误差绝对值对比 Figure 5 The absolute values′ comparison of the prediction errors between the online model and the offline model based on the MAG-FASTRVM |
通过观察图 5可知,MAG-FASTRVM的在线模型和离线模型进行BOD5检测时在大多数情况下都能达到较满意的预测效果.而对COD进行预测时,在大多数工况点处在线模型的预测误差均明显低于离线模型的误差.这说明在线模型的COD输出精度较离线模型得到了显著的提高.观察图 4也可发现MAG-FASTRVM在线模型对污水参数BOD5、COD表现出良好的跟踪能力,实时性较好.
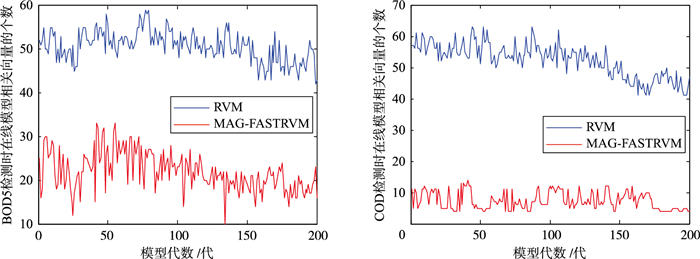
表 4、表 5给出了MAG-FASTRVM及其对比模型的在线实验结果.由表 4、表 5可发现,几种模型的在线预测效果均比离线模型要好,这表明在线模型对污水出水参数BOD5、COD的变化具有更好的适应性.与SVM、RVM及其它混合核函数的相关向量机相比,MAG-FASTRVM的预测精度中等,但是其模型稀疏性和运行时间都比其它对比模型要好.通过对表 4、表 5中RVM与SVM的预测精度、模型稀疏性和运行时间等性能指标进行分析可发现,RVM比SVM更适合作为污水的在线预测模型.图 6是RVM与MAG-FASTRVM的稀疏性对比曲线,其显示了BOD5和COD检测时200代在线更新模型中的相关向量的个数.可以看出,无论是检测BOD5或COD,MAG-FASTRVM模型的相关向量个数都明显较RVM要少.
| 预测算法 | 均方根误差 | 相关向量个数/个 | 运行时间/s |
| SVM | 0.017 4 | 75 | 340.249 1 |
| RVM | 0.021 8 | 60 | 36.057 76 |
| FASTRVM | 0.034 2 | 36 | 25.477 286 |
| MUPL-FASTRVM | 0.043 0 | 25 | 19.545 296 |
| C-FASTRVM | 0.034 5 | 33 | 24.800 076 |
| MAG-FASTRVM | 0.039 6 | 21 | 17.051 350 |
| 预测算法 | 均方根误差 | 相关向量个数/个 | 运行时间/s |
| SVM | 0.037 6 | 80 | 465.433 4 |
| RVM | 0.035 3 | 52 | 47.7401 1 |
| FASTRVM | 0.042 4 | 39 | 39.526 25 |
| MUPL-FASTRVM | 0.050 4 | 31 | 43.176 79 |
| C-FASTRVM | 0.041 8 | 20 | 28.515 41 |
| MAG-FASTRVM | 0.039 4 | 7 | 14.953 07 |
|
| 图 6 两种模型稀疏性对比 Figure 6 Sparseness comparison between the two models |
结合图 6分析可知,MAG-FASTRVM模型在线预测有着精度高、稀疏性好、更新速度快等优点.考虑到实时预测的需要,软测量模型对快速性有着更高的要求.在满足预测精度的前提下,有快速更新功能的模型更适合用于出水参数BOD5、COD的在线预测.因此,MAG-FASTRVM的在线模型比起其它在线模型更能满足实时预测的要求.
3 结论污水参数COD、BOD5的实时测量对水质污染防治和监测具有十分重要的作用.为解决离线测量模型对污水参数进行实时快速预测存在现实困难的问题,本文提出了基于MAG-FASTRVM的在线软测量模型.在线建模实验表明基于MAG-FASTRVM的在线模型输出精度高、稀疏性好、学习时间短且更新速度快.在满足预测精度的前提下,该模型相较于离线测量模型更适合用于对出水参数BOD5、COD的在线预测,具有良好的实用性和有效性.
| [1] |
胡俊刚, 胡雪梅.
城镇污水处理厂运营现状及自动化控制的应用[J]. 武汉理工大学学报, 2002, 11(24): 66–69.
Hu J G, Hu X M. Management and automatically control in water treatment[J]. Journal of Wuhan University of Technology, 2002, 11(24): 66–69. |
| [2] | Chen Z B, Ren Y M. Sewage treatment plant measurement, automatic control and fault diagnosis[M]. Beijing: Chemical Industry Press, 2009: 16-18. |
| [3] |
任东红, 韩红桂, 乔俊飞.
基于IHPSO算法的污水处理过程集成神经网络软测量模型[J]. 信息与控制, 2014, 43(1): 123–128.
Ren D H, Han H G, Qiao J F. Hierarchically neural network soft measurement modeling based on IHPSO algorithm for wastewater treatment process[J]. Information and Control, 2014, 43(1): 123–128. |
| [4] |
乔俊飞, 鞠岩, 韩红桂.
基于自组织随机权神经网络的BOD软测量[J]. 北京工业大学学报, 2016, 42(10): 1451–1460.
Qiao J F, Ju Y, Han H G. BOD soft-sensing based on SONNRW[J]. Journal of Beijing University of Technology, 2016, 42(10): 1451–1460. DOI:10.11936/bjutxb2016040021 |
| [5] | 乔俊飞, 李瑞祥, 柴伟, 等. 基于PSO-ESN神经网络的污水BOD预测[J]. 控制工程, 2016, 23(4): 463-467. |
| [6] |
田奕, 乔後飞.
基于遗传算法的BOD神经网络软测量[J]. 计算机技术与发展, 2009, 19(3): 127–129.
Tian Y, Qiao J F. NN soft-measuring for BOD predict based on GA[J]. Computer Technology and Development, 2009, 19(3): 127–129. |
| [7] | Li G H, Zheng H. Application of artificial neural network in wastewater treatment[C]//Second International Conference on information Science and Engineering. Piscataway, NJ, USA: IEEE, 2010: 4373-4375. |
| [8] |
宋贤民. 基于SVM的污水处理过程软测量建模研究[D]. 江西: 南昌大学, 2007. Song X M. Study on soft sensor model of wastewater measuring based on SVM[D]. Jiangxi: Nanchang University, 2007. |
| [9] |
徐方舟, 潘丰.
基于PSO-LSSVM污水处理系统出水数据的软测量[J]. 江南大学学报:自然科学版, 2010, 9(3): 253–256.
Xu F Z, Pan F. Soft sensing of the parameters in sewage disposal system based on PSO-LSSVM[J]. Journal of Jiangnan University:Natural Science Edition, 2010, 9(3): 253–256. |
| [10] |
张杰, 张建秋, 冯辉.
支持向量机和神经网络联合软测量SBR污水处理中COD的方法[J]. 传感技术学报, 2009, 22(10): 1519–1524.
Zhang J, Zhang J Q, Feng H, et al. SVM and neural networks joint approach to the soft measurement of COD values in SBR wastewater treatment systems[J]. Chinese Journal of Sensors and Actuators, 2009, 22(10): 1519–1524. DOI:10.3969/j.issn.1004-1699.2009.10.029 |
| [11] |
张昭昭.
污水处理过程出水水质多模型在线软测量方法[J]. 控制工程, 2014, 21(1): 88–93.
Zhang S S. An online multi-model softsensing method of water quality in wastewater treatment process[J]. Control Engineering of China, 2014, 21(1): 88–93. |
| [12] |
丛秋梅, 张北伟, 苑明哲.
基于同步聚类的污水水质混合在线软测量方法[J]. 计算机工程与应用, 2015, 51(24): 27–34.
Cong Q M, Zhang B W, Yuan M Z. On-line soft sensor for water quality of wastewater based on synchronous clustering[J]. Computer Engineering and Applications, 2015, 51(24): 27–34. DOI:10.3778/j.issn.1002-8331.1507-0314 |
| [13] |
丛秋梅, 苑明哲, 王宏.
基于稳定Hammerstein模型的在线软测量建模方法及应用[J]. 化工学报, 2015, 66(4): 1380–1386.
Cong Q M, Yuan M Z, WANG H. On-line soft sensor based on stable Hammerstein model and its applications[J]. CIESC Journal, 2015, 66(4): 1380–1386. |
| [14] |
柳长源. 相关向量机多分类算法的研究与应用[D]. 哈尔滨: 哈尔滨工程大学, 2013. Liu C Y. Research and application on the multi-classification of relevance vector machine algorithm[D]. Harbin: Harbin Engineering University, 2013. |
| [15] | Pani A K, Mohanta H K. Soft sensing of particle size in a grinding process:Application of support vector regression, fuzzy inference and adaptive neuro fuzzy inference techniques for online monitoring of cement fineness[J]. Powder Technology, 2014, 264(3): 484–497. |
| [16] | Tipping M E. Sparse Bayesian learning and the relevance vector machine[J]. Journal of Machine Learning Research, 2001, 1(3): 211–244. |
| [17] |
许玉格, 刘莉, 曹涛.
基于Fast-RVM的在线软测量预测模型[J]. 化工学报, 2015, 66(11): 4540–4545.
Xu Y G, Liu L, Cao T. On-line soft measuring model based on Fast-RVM[J]. CIESC Journal, 2015, 66(11): 4540–4545. |
| [18] | Masuda Kazuaki. Global optimization of point search by equilibrium search of gradient dynamical system[J]. Electronic and Communication in Japan, 2008, 91(1): 19–31. DOI:10.1002/ecj.v91:1 |
| [19] | Su J, Wang X, Liang Y, et al. GA-based support vector machine model for the prediction of monthly reservoir storage[J]. Journal of Hydrologic Engineering, 2014, 19(7): 1430–1437. DOI:10.1061/(ASCE)HE.1943-5584.0000915 |
| [20] | Buchgraber T, Shutin D, Poor H V. A sliding-window online fast variational sparse Bayesian learning algorithm[C]//Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing. Piscataway, NJ, USA: IEEE, 2011: 2128-2131. |
| [21] | Faul A, Avenuse J J T. Fast marginal likelihood maximisation for sparse Bayesian models[C]//Proceedings of the Ninth International Workshop on Artificial Intelligence & Statistics. Piscataway, NJ, USA: IEEE, 2003: 3-6. |
| [22] |
杨国鹏, 周欣, 余旭初.
稀疏贝叶斯模型与相关向量机学习研究[J]. 计算机科学, 2010, 37(7): 225–228.
Yang G P, Zhou X, Xu X C. Research on sparse Bayesian model and the relevance vector machine[J]. Computer Science, 2010, 37(7): 225–228. |
| [23] |
许玉格, 曹涛, 罗飞.
基于相关向量机的污水处理出水水质预测模型[J]. 华南理工大学学报:自然科学版, 2014, 42(5): 103–107.
Xu Y G, Cao T, Luo F. The prediction of effluent quality of waste water treatment based on relevance vector machine[J]. Journal of South China University of Technology:Natural Science Edition, 2014, 42(5): 103–107. |
| [24] | Manel P. Water treatment plant data set[DB/OL]. (1993-06-01)[2013-01-01]. http://archive.ics.uci.edu/ml/datasets/Water+Treatment+Plant. |



