2. 江南大学轻工过程先进控制教育部重点实验室, 江苏 无锡 214122
2. Key Laboratory of Advanced Process Control for Light Industry(Ministry of Education), Jiangnan University, Wuxi 214122, China
0 引言
工业生产过程的复杂程度正在日益增加,往往伴随着多工况、非线性和时变等过程特征,其计算机监控系统提取的信息也越来越丰富,推动了基于数据驱动方法的软测量建模理论的发展[1-2].随着实际生产过程中采集数据量的增加,数据信息的维度越来越高[3-4],然而高维数据中往往存在着大量的冗余信息,为传统的软测量建模方法带来了新的挑战.
针对具有多个稳态工作点或者多工况的复杂工业生产过程,多模型建模是一种有效的软测量技术[5-6],将建模数据进行准确分类又是保证多模型建模预测性能的前提之一.对低维数据进行聚类时,传统的聚类方法均可以取得较好的聚类结果;然而对于高维数据,由于数据本身的特点和传统聚类算法自身的局限性,使得聚类很难取得较满意的结果.因此,常用的高维数据聚类算法的主要思想是先对高维数据进行合理的降维或空间划分处理,然后再用传统的聚类方法在低维空间中完成聚类[3, 7].
另一方面,多模型软测量建模方法在预测最终的输出时,需要对各局部模型的预测值进行集成.常用的集成方式主要分为两种:开关切换方式和加权融合方式.其中,开关切换方式只选择可能性最大的局部模型进行预测,很难对全局模型进行准确描述,而加权融合方式可根据新来样本与各局部模型的某些指标,计算得到其隶属于各局部模型的概率[8-9],融合各局部模型的预测值即可得到较准确的预测结果.因此,在软测量建模领域,加权融合集成方式得到了广泛的研究和应用.
针对上述问题,提出一种改进仿射传播聚类的多模型软测量方法.利用主成分分析(principal component analysis,PCA)[3, 7, 10]方法和差分进化算法(differential evolution,DE)[11-12]对传统的仿射传播(affinity propagation,AP)[13-15]聚类算法进行改进,使算法对高维数据进行聚类时,可以取得更好的聚类结果,划分得到全局最优的子数据集,并用高斯过程回归(Gaussian process regression,GPR)[16-18]方法建立各局部预测模型.对于新来的样本,利用各局部模型的预测方差计算得到新来样本隶属于各局部模型的概率,有效地融合各局部模型的预测值得到最终的预测输出,从而实现对一些复杂工业生产过程中关键变量的预测.
1 一种改进的仿射传播聚类算法 1.1 仿射传播聚类算法AP聚类是一种新型的聚类算法,聚类初始时将所有数据点作为潜在的聚类中心,聚类过程中各数据点通过迭代竞争聚类中心,得到的聚类结果与数据的真实特性更加吻合.目前,该方法在图像处理、文本聚类等领域已经得到了广泛的应用.
AP是一种基于样本相似度矩阵S进行聚类的方法.给定训练样本集D={(xi,yi)}(i=1,2,…,n),定义任意两个样本xi和xk之间的相似度为欧氏距离平方的负值,即S(i,k)=-‖xi-xk‖2.相似度矩阵主对角线上的元素S(k,k)称作偏置参数.初始化相似度矩阵时,偏置参数一般取相同值,其值越大,产生的聚类数目越多,可通过改变其值调整聚类的结果.同时,在AP聚类过程中,还引入了两个重要的证据信息:证据R(i,k)描述点k适合作为点i的聚类中心的程度,证据A(i,k)描述点i认可点k作为其聚类中心的程度.对于样本点i,若样本点k对应的两个证据之和为所有样本点中的最大值,则点k就是点i的聚类中心.仿射传播聚类算法通过不断地搜集更新证据R(i,k)和A(i,k),直到迭代产生稳定的聚类中心和类别归属情况,或者迭代达到最大次数.
迭代更新公式分别为
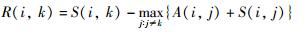
|
(1) |
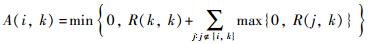
|
(2) |
为避免在迭代过程中发生震荡,引入阻尼系数λ,更新公式为
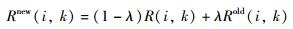
|
(3) |
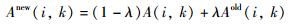
|
(4) |
式中,Rnew(i,k)和Anew(i,k)为当前迭代的值,Rold(i,k)和Aold(i,k)为前一次迭代的值.
1.2 基于PCA改进的AP聚类算法在对高维数据进行聚类的过程中,数据各属性之间不可避免地存在着信息重叠的情况.如果对存在高度共线性的数据不加以处理而直接聚类的话,容易造成信息的重复计算,会放大共线性属性的作用而淹没独立性指标的贡献,使聚类难以取得较满意的结果.因此,应用传统的聚类算法对高维数据进行聚类时,可以先对原始数据进行处理,去除数据空间中冗余的信息,以提高聚类的精度[7].
PCA是一种经典的数据降维方法.给定样本数据集X∈Rn×m,其中n为数据集样本数目,m是样本数据的维度.假设PCA降维后得到q个主成分,则原始数据X可以表示为
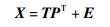
|
(5) |
式中,T∈Rn×q是主成分子空间的得分矩阵,P∈Rm×q是主成分子空间相应的载荷矩阵,E是残差矩阵.
PCA方法可将原有错综复杂的数据通过线性变换转化为少数相互独立的主成分数据,在降低数据维度的同时还能最大限度地保留原始数据中所包含的信息,使高维数据对象的特征更加明显,在数据降维和特征提取领域得到了广泛的应用.利用PCA方法对高维数据进行处理时,一般要求主成分的累计贡献率在85%以上,以保证损失少量信息的前提下,充分达到降维的目的.
基于以上分析,可以利用PCA方法对AP聚类算法进行改进,在对高维数据进行聚类时,先利用PCA方法进行降维处理,然后再利用AP聚类算法对降维后的得分矩阵进行聚类.改进后方法的聚类效果与分析可参考第4.1.1小节.
1.3 基于DE的AP算法参数的优化传统的AP算法中,偏置参数p一般取相似度矩阵元素最小值的倍数,或通过不断调整以达到较好的聚类结果,阻尼系数λ的取值一般介于0.5~0.9之间,往往只通过修改p的取值对聚类的结果进行调整[3],忽略了λ对聚类的影响.由AP算法的聚类原理可知,p和λ的取值都会影响到聚类的结果,而且在没有先验知识的情况下,由于p和λ取值的不确定性,在很大程度上限制了AP算法的应用范围.针对上述问题,可以通过建立聚类结果评价指标与AP算法参数值之间的关系,确定一组较优的参数值,使AP算法产生较好的聚类结果.
Silhouette[3, 7]指标是一种有效的聚类结果评价指标,可对聚类划分所得数据集的类内紧密性和类间可分性进行综合分析与评价,其值介于-1~1之间,指标值越大说明类内紧密程度越高且类间可分性越大,即聚类的效果越好.已知n个数据样本聚类后得到K个子数据集,分别为Ci(i=1,2,…,K),其中样本t属于Ci,则样本t的Silhouette指标计算公式为
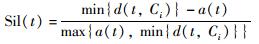
|
(6) |
式中,d(t,Ci)为样本t到另外一个类中所有样本的平均距离,a(t)为样本t到Ci类中其它所有样本的平均距离.可用n个数据Silhouette指标的平均值,即Silhouette=mean(sum(Sil(t))),来评价聚类结果的质量.
DE算法是一种基于群体智能的随机搜索算法,通过模拟自然界生物优胜劣汰的进化规律,不断地进行变异、交叉和选择操作,引导搜索过程向全局最优解逼近.针对AP算法中参数确定缺乏依据的问题,可利用DE算法对AP算法进行改进(简称DEAP方法),以反映聚类结果的Silhouette指标作为目标函数,对偏置参数和阻尼系数进行寻优,从而得到较好的聚类结果.该优化问题可以表述为
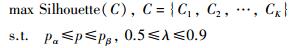
|
(7) |
式中,C1,C2,…,CK为聚类所得的K个子数据集,pα和pβ为偏置参数p大致的取值范围,可根据经验或试凑法得到.
利用DE算法优化AP参数的实现步骤为:
1) 确定DE算法控制参数,如种群大小、最大迭代次数等,然后初始化种群并计算初始种群中个体对应的Silhouette指标;
2) 对种群进行变异、交叉操作,得到实验参数值,代入AP算法对数据集进行聚类,计算对应聚类结果的Silhouette指标,并根据Silhouette指标进行优胜劣汰的选择操作;
3) 若Silhouette指标达到指定精度或进化代数达到最大次数,则算法终止,否则返回步骤2);
4) 根据所得参数值对数据集进行聚类.
在有聚类数目先验知识的情况下,可按照先验知识对差分进化算法的寻优过程进行限制,若寻优过程中种群个体参数值进行计算得到的聚类数目与已知的数目不同,则舍弃该个体;若没有先验知识,可将聚类的数目限制在2~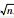
综上所述,本文提出一种基于PCA和DE算法的改进AP聚类方法(简称PCA-DEAP方法),对传统的AP算法进行全面改进.算法的主要原理是先利用PCA方法对原始数据进行降维处理,然后再利用DE改进的AP方法在低维空间中对得分矩阵进行聚类.算法的难点是如何协调好降维后主成分个数和AP算法中偏置参数、阻尼系数之间的关系,使聚类可以取得较好的结果.
由PCA的原理可知,主成分个数较少时,得分矩阵可能会丢失原始数据中的重要信息;主成分个数较多时,得分矩阵维度较高,达不到数据降维的目的,因此主成分的选取直接影响着聚类的结果.本文先根据累计贡献率确定主成分个数,然后得到对应的得分矩阵,并利用DE改进的AP算法对所得得分矩阵进行聚类,再对所得聚类结果进行对比,选取全局最优的聚类结果.算法的主要流程如图 1所示.
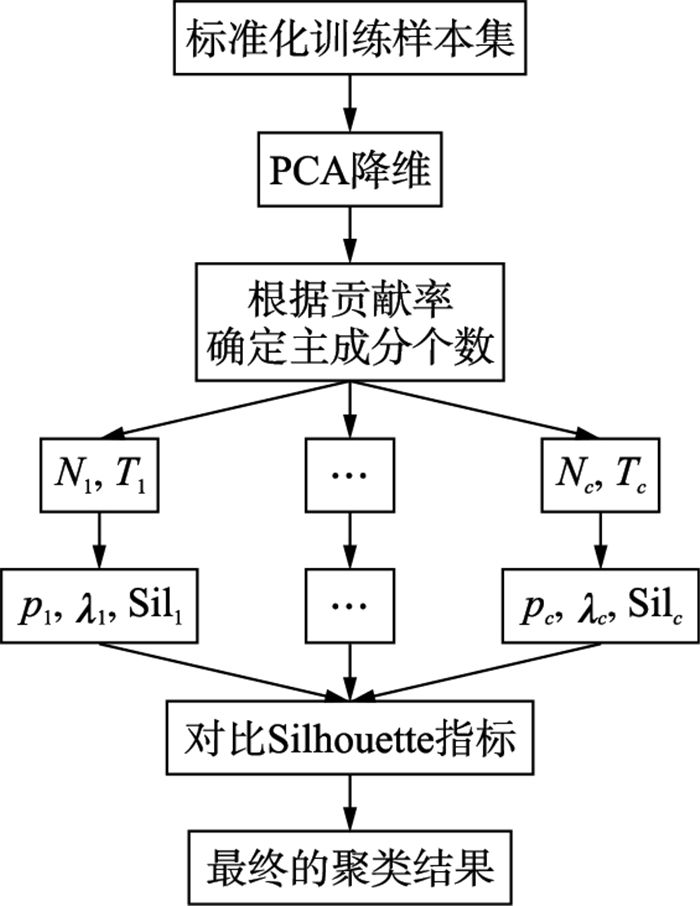
|
| 图 1 改进的AP聚类算法 Figure 1 The improved AP clustering algorithm |
改进的AP算法执行步骤为:
1) 对原始训练样本进行标准化处理,去除样本各属性不同量纲和数量级的影响;
2) 对标准化后的数据进行PCA降维处理,并根据贡献率确定主成分个数Nc和对应的得分矩阵Tc,其中c=1,2,…,C;
3) 利用DE改进的AP算法对不同主成分取值时对应的得分矩阵进行聚类,确定不同主成分取值情况下的较优的偏执参数和阻尼系数取值,以及对应的Silhouette指标;
4) 对比不同主成分个数情况下的Silhouette指标,选取指标最高值对应的聚类结果为最终的聚类结果.
2 多模型建模方法 2.1 高斯过程回归方法给定训练样本集D={(xi,yi)}(i=1,2,…,n),其中xi∈Rd代表d维输入,yi∈R代表 1维输出数据,n为训练样本个数.对于一个新来数据xnew,其对应预测输出的均值和方差,分别由式(8)~式(9)计算得到:
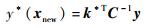
|
(8) |
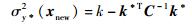
|
(9) |
式中,k*=[k(xnew,x1),…,k(xnew,xn)]T是训练样本和测试输入之间的n×1维协方差矩阵,C= Σ+σn2I是训练样本之间的n×n维协方差矩阵,σn2表示噪声方差,k是测试输入和自身的协方差.
在保证对于任意输入产生的协方差矩阵满足非负正定的条件下,本文采用高斯协方差函数:
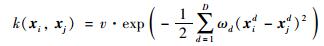
|
(10) |
式中,v表示先验知识的总体度量,ωd代表每个成分xd的相关性程度.
上述协方差函数确定后,需要对未知参数θ=[v,σn2,ω1,…,ωD]进行估计,一般通过极大似然法求解:
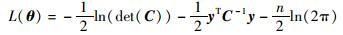
|
(11) |
可先将θ设为一个合理范围内的随机值,然后用共轭梯度法来搜索参数的最优值.求得参数后,对于新来的样本xnew,通过式(8)和式(9)进行计算即可得到相应的输出值.
2.2 基于预测方差的贝叶斯融合为得到多模型最终的预测输出,需要对各个局部模型的预测值进行融合,因此局部模型的权值计算方法对软测量模型的预测精度具有重要影响.传统方法中,新来样本隶属于各局部模型的权值一般通过xnew到各子数据集聚类中心的距离计算得到[19].近几年,基于模型预测能力或者预测值不确定性计算后验概率的方法得到了广泛应用[5, 8].从式(8)和式(9)可以看出,GPR方法建立的软测量模型在对新来样本进行预测时,不仅可以输出该样本的预测值,还能得到预测方差.预测方差越小,说明建立的GPR模型对当前样本的预测值越准确,基于此原理,提出一种基于预测方差计算后验概率的方法.
相关根预测方差(relative-root prediction variance,RPV)[20]可以用于描述软测量模型对训练样本预测的效果,其值越小,说明模型的预测性能越好.定义软测量模型LM对训练样本xi的相关根预测方差为
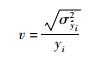
|
(12) |
其中,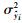
利用改进的AP算法将训练样本划分为K个子数据集,并用GPR方法建立各个局部模型,记作LMk(k=1,…,K).对于新来的样本xnew,基于贝叶斯定理,最终的预测结果可以表示为
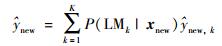
|
(13) |
式中,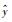
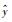
由贝叶斯定理知,后验概率可用式(14)计算:
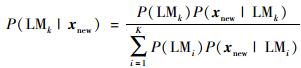
|
(14) |
式中,P(LMk)为第k个局部模型的先验概率,P(xnew|LMk)为xnew隶属于第k个局部模型的条件概率.
若没有先验知识,每个局部模型的先验概率可被简单地定义为
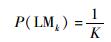
|
(15) |
鉴于GPR方法所建软测量模型输出具有概率意义,将相关根预测方差引入到P(xnew|LMk)的计算过程中:
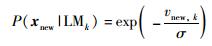
|
(16) |
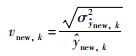
|
(17) |
式中,σ为缩放因子,可根据不同的应用进行调整,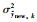
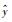
可以看出,如果第k个局部模型对当前样本的相关根预测方差越小,则该模型预测值对应的权值P(LMk|xnew)越大,表明当前样本更适合用该模型进行预测输出.
3 基于改进AP算法的软测量建模步骤综上分析,本文提出的多模型软测量建模的详细步骤为:
1) 利用改进的AP方法对原始训练样本进行聚类,得到M个子数据集;
2) 用GPR方法建立各子数据集的局部预测模型;
3) 当有新样本xnew到来时,计算得到各局部模型对当前样本的预测值和预测方差,并根据预测方差计算得到xnew隶属于各局部模型的概率;
4) 利用式(13)对各局部模型的预测值进行融合,即可得到最终的预测输出.
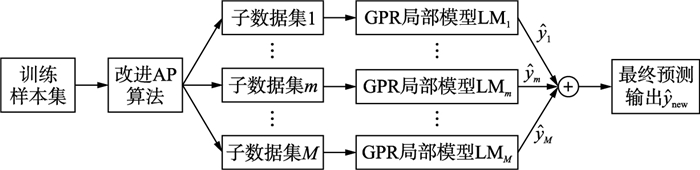
|
| 图 2 基于改进AP聚类的软测量建模 Figure 2 Soft sensor modeling based on improved AP algorithm |
首先为了分析所提改进算法的聚类效果,采用UCI数据库(http://archive.ics.uci.edu/ml/)中的Wine和SPECTF数据集进行仿真实验.其中,Wine数据集共有178个样本数据,每个样本有13个属性,分为3类;SPECTF数据集共有187个样本数据,每个样本有44个属性,分为2类.
4.1.1 PCA-AP和AP方法对比聚类过程中,两种算法的偏置参数均取相似度矩阵最小值的倍数,即p=β·min(S),β取值介于0.5~4之间,取值间隔为0.01,阻尼系数λ取值介于0.5~0.9之间,取值间隔为0.1.在利用PCA-AP方法对Wine数据进行聚类时,取其累计贡献率为89%时的得分矩阵,在对SPECTF数据进行聚类时,取其累计贡献率为85%时的得分矩阵.用Silhouette指标对聚类的结果进行评价,所得结果如图 3和图 4所示.
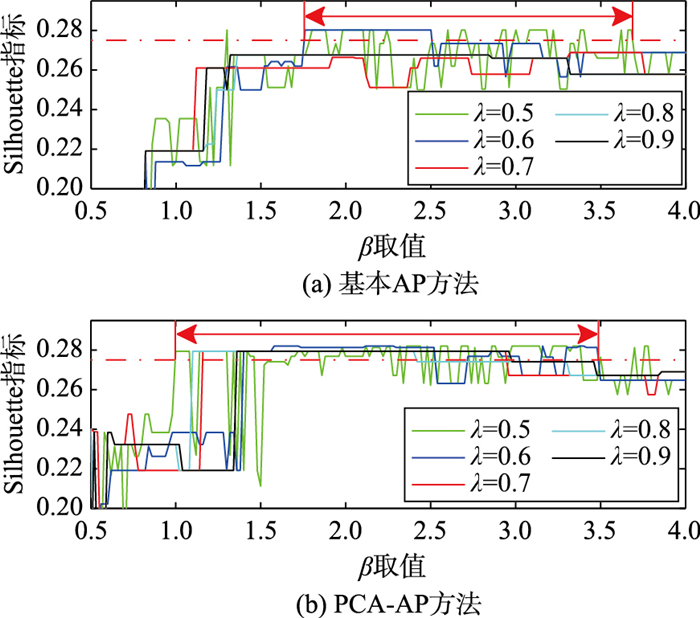
|
| 图 3 Wine数据集聚类结果 Figure 3 Clustering results of Wine dataset |
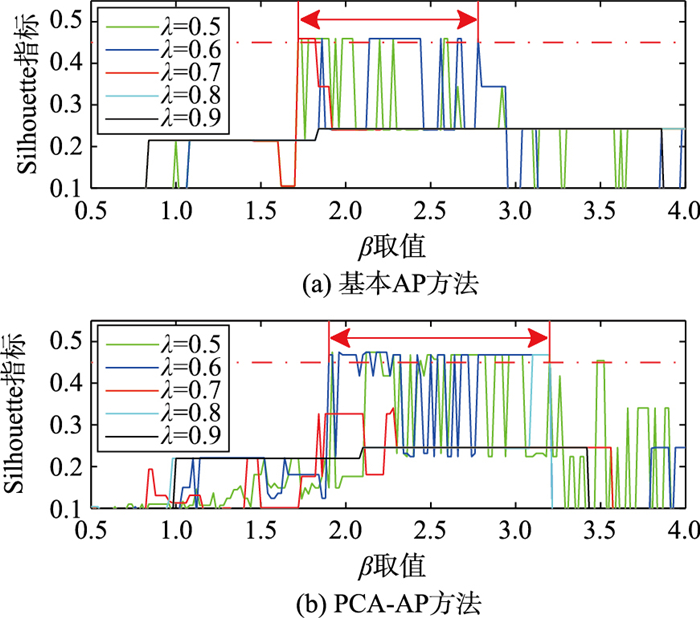
|
| 图 4 SPECTF数据集聚类结果 Figure 4 Clustering results of SPECTF dataset |
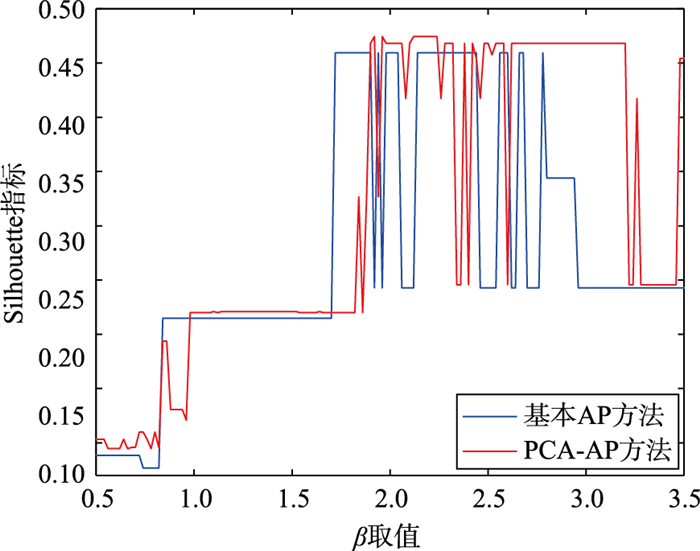
从图中可以看出,λ不同取值情况下,所得的聚类结果不同,因此λ的取值对AP聚类具有重要影响,在λ取值不合理的情况下,很难得到较好的聚类结果.相比于基本AP方法,在参数取值和范围均相同的情况下,PCA-AP方法取得Silhouette指标较高值的范围更广一些,且更为密集,说明使用PCA-AP方法对高维数据进行聚类时,更容易取得较好的聚类结果.
为更好地对比两种算法的聚类结果,取两种算法相同β取值情况下不同λ取值时对应Silhouette指标的最大值进行对比,所得结果如图 5和图 6所示.比较可以看出,相比基本AP方法,PCA-AP方法可以取得更高的Silhouette指标值,说明当对高维数据进行聚类时,使用PCA方法对AP算法进行改进,可以有效地提高聚类的精度.
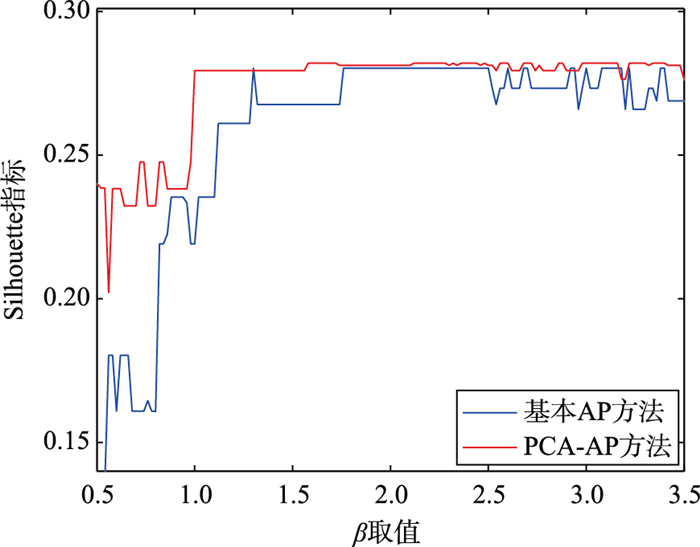
|
| 图 5 Wine数据集聚类结果 Figure 5 Clustering results of Wine dataset |
|
| 图 6 SPECTF数据集聚类结果 Figure 6 Clustering results of SPECTF dataset |
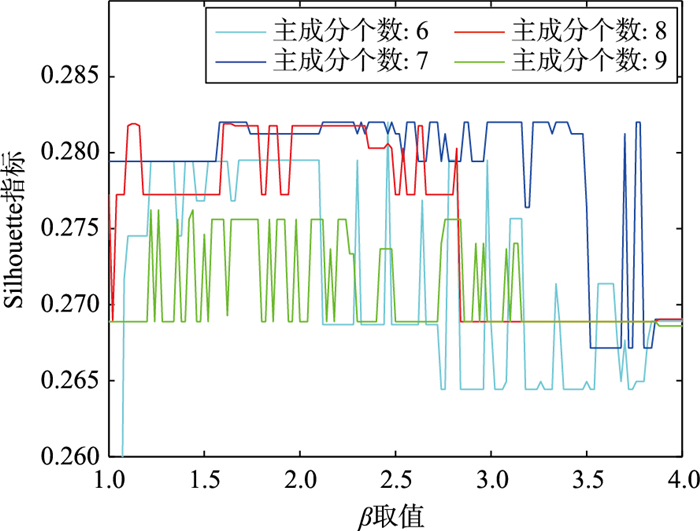
图 7为使用PCA-AP方法对Wine数据集进行聚类时,不同主成分个数情况下所得聚类结果的比较.从图中可以看出,由于降维时选取的主成分个数不同,所得得分矩阵不同,导致聚类结果也不同,即PCA-AP方法的聚类结果受选取主成分个数的影响,而且在主成分个数取值不合理的情况下,使用PCA-AP方法取得的结果可能会适得其反,因此需要对PCA-AP方法进行改进,以保证取得较好的聚类结果.
|
| 图 7 主成分个数不同取值情况下Wine数据集聚类结果 Figure 7 Clustering results of Wine dataset with different principal component number |
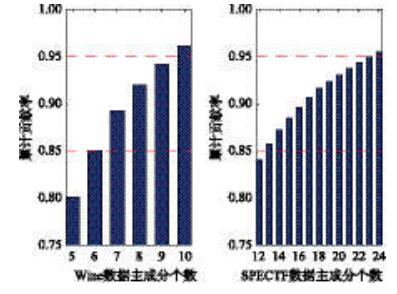
从4.1.1小节的分析可以看出,主成分个数的取值对聚类结果具有重要影响.由PCA的原理可知,累计贡献率取值较低时,得到的主成分个数较少,降维后的数据可能会丢失原有数据中包含的重要信息,累计贡献率取值较高时,得到的主成分个数较多,达不到数据降维的效果.为达到保留主要信息且充分降低数据维度的目的,可将累计贡献率的范围设置为85%~95%.
图 8分别为Wine和SPECTF数据的主成分对应的累计贡献率图.从图中可以看出,针对Wine数据,当主成分个数取值为6~9时,累计贡献率在85%~95%之间,针对SPECTF数据,对应的主成分个数取值为13~23.
|
| 图 8 PCA特征提取 Figure 8 PCA feature extraction |
两种聚类算法对数据集的聚类结果分别如表 1和表 2所示.由于SPECTF数据经PCA方法降维后累计贡献率在85%~95%之间的情况较多,所以只列举了表 2中几种主成分情况下的聚类结果.分析表中的数据可以看出,Silhouette指标值较高时,聚类结果的正确率也相对较高,说明以Silhouette指标为目标函数对AP算法的参数进行寻优是一种有效的方法.当对高维数据进行聚类时,相比直接对数据进行聚类的DEAP方法,PCA-DEAP方法通过对高维数据进行降维处理,去除了部分冗余信息并降低了计算复杂度,有效地提高了算法对高维数据的处理能力.
| 评价指标 | PCA-DEAP方法主成分个数 | DEAP 方法 |
|||
| 6 | 7 | 8 | 9 | ||
| 贡献率 | 85.098 | 89.337 | 92.018 | 94.240 | - |
| Silhouette | 0.280 | 0.282 | 0.281 | 0.276 | 0.280 |
| 正确率 | 95.506 | 96.629 | 96.067 | 94.944 | 94.944 |
| 评价指标 | PCA-DEAP方法主成分个数 | DEAP 方法 |
|||
| 13 | 16 | 19 | 23 | ||
| 贡献率 | 85.748 | 89.679 | 92.406 | 94.99 | - |
| Silhouette | 0.474 | 0.468 | 0.473 | 0.471 | 0.459 |
| 正确率 | 83.422 | 81.818 | 82.353 | 82.888 | 82.888 |
为验证本文所提软测量建模方法的有效性,对某污水厂污水处理过程中出水水质的生化需氧量(BOD)进行软测量建模.BOD是一种水体污染状况的检测指标,与污水处理过程中各反应阶段的悬浮物浓度、可降解固体浓度、生化需氧量和化学需氧量等参数具有密切的关系,因此选取与BOD相关的19个变量作为辅助变量用于软测量建模.共采集了195组数据,取其中2/3共130组数据作为训练样本,剩下的1/3共65组数据作为测试样本.
为进一步对比分析本文所提软测量建模方法的预测性能,将不同的聚类和融合方法进行组合.方法1采用PCA-DEAP算法对原始训练样本集进行聚类,基于新来样本到各子数据集聚类中心的距离计算得到其隶属于各局部模型的概率,融合各局部模型的预测值得到最终的预测输出,简称PCA-DEAP-距离方法;方法2采用DEAP算法对原始训练样本进行聚类,采用本文中基于预测方差的方法计算新来样本隶属于各局部模型的概率,简称DEAP方法;方法3为本文所提的软测量建模方法.仿真结果使用均方根误差(RMSE)、最大误差(MAXE)和跟踪性能指标(TP)作为评价指标:
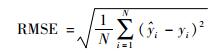
|
(18) |
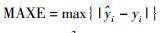
|
(19) |
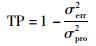
|
(20) |
式中,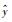
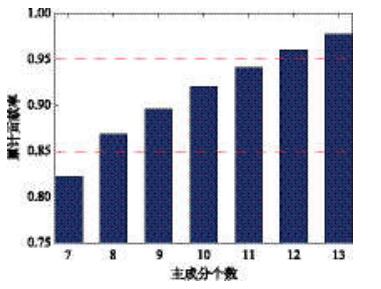
图 9为污水数据集主成分对应的累计贡献率图,从图中可以看出,当主成分个数为8~11时,对应的累计贡献率在85%~95%之间.
|
| 图 9 PCA特征提取 Figure 9 PCA feature extraction |
表 3为两种聚类方法对训练样本进行聚类的结果对比.由于污水处理过程中的数据存在着大量的冗余信息,因此利用PCA-DEAP方法进行聚类所得结果的Silhouette指标明显高于直接聚类的DEAP方法.根据本文所提方法,选取累计贡献率在85%~95%之间最高的Silhouette指标值对应的聚类结果为最终的聚类结果,因此,在以下的仿真中,本文方法选取的主成分个数为8,对应聚类结果的Silhouette指标为0.274,并基于此聚类结果建立软测量模型对出水的BOD浓度进行预测.
| 评价指标 | PCA-DEAP方法主成分个数 | DEAP 方法 |
|||
| 8 | 9 | 10 | 11 | ||
| 贡献率 | 86.851 | 89.59 | 92.077 | 94.154 | - |
| Silhouette | 0.274 | 0.260 | 0.253 | 0.246 | 0.205 |
图 10为3种软测量建模方法对污水处理过程中出水BOD浓度的预测值和真值对比曲线,从图中可以看出,几种建模方法均取得了较好的预测结果,均能对污水处理过程中出水的BOD浓度进行较准确的预测.
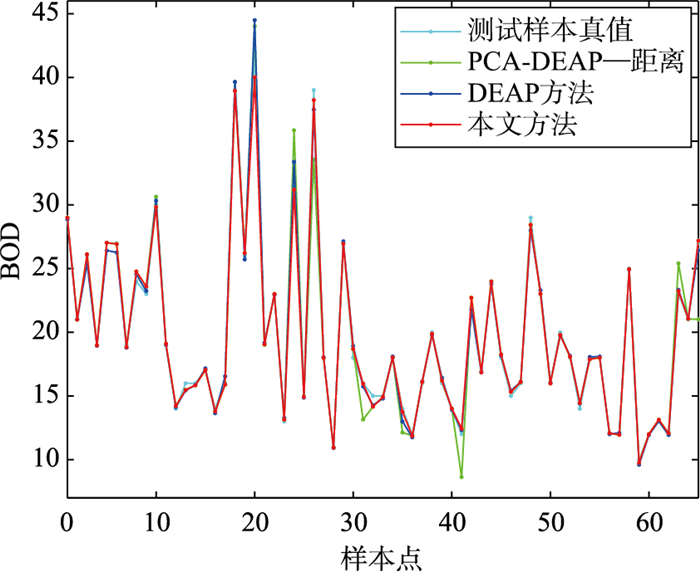
|
| 图 10 BOD预测结果 Figure 10 Prediction results of BOD |
图 11为3种软测量建模方法对污水处理过程中出水BOD浓度预测的绝对误差图,表 4为3种方法预测结果的对比.对比分析可以看出,在数据维度较高且归一化后数据分类不明显的情况下,基于新来样本到各子数据集聚类中心的距离计算其隶属于各局部模型概率的方法,无法有效地计算新来样本的隶属度,因此在预测输出时容易出现较大的预测误差,而基于预测方差的方法可根据各局部模型对当前样本的预测能力对其隶属度进行计算,所建软测量模型具有更高的预测精度.对包含冗余信息的高维数据进行聚类时,直接聚类的方法容易受冗余信息的影响,往往难以取得较好的聚类结果,所以基于此分类结果建立软测量模型的预测性能会受到影响,而本文改进的AP方法可对高维数据进行合理的降维处理,所得结果能较准确地反映数据集的分类情况,所以基于此分类结果建立的软测量模型取得了较好的预测结果.从以上的比较可以看出,本文所提软测量建模方法具有较高的预测精度,能对污水处理过程中出水的BOD浓度进行有效预测.
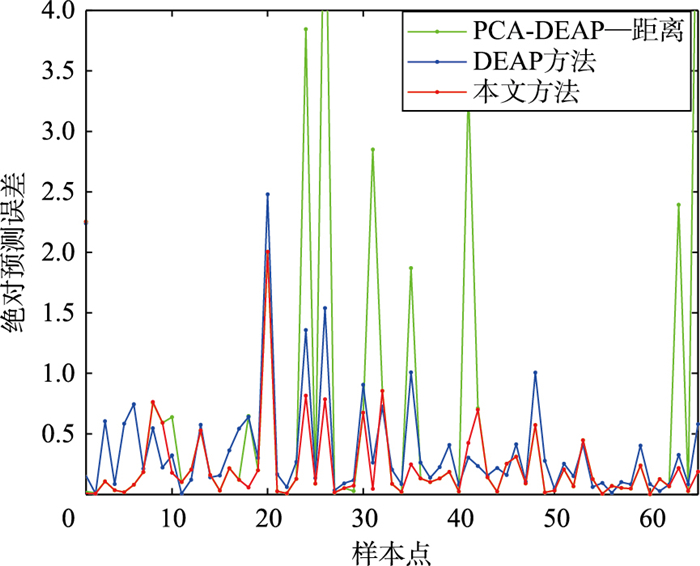
|
| 图 11 绝对预测误差 Figure 11 The absolute prediction error |
| 分类方法 | 组合方式 | RMSE | MAXE | TP |
| PCA-DEAP | 距离 | 1.348 | 5.984 | 0.962 |
| DEAP | 预测方差 | 0.538 | 2.480 | 0.994 |
| PCA-DEAP | 预测方差 | 0.388 | 2.005 | 0.997 |
针对具有高维度、多工况特性的复杂工业生产过程,从数据处理和聚类方法参数优化两个角度,提出一种改进AP聚类的多模型软测量方法.利用PCA和DE算法对传统的AP算法进行改进,使AP算法在对高维数据进行聚类时,可以避免冗余信息的影响,同时解决了AP算法中参数的优化求解问题,有效地提高了聚类的精度;同时,利用基于预测方差的方法计算得到新来样本隶属于各局部模型的概率,融合各局部模型预测值得到较准确的预测结果.仿真结果表明,本文提出的软测量建模方法取得了良好的预测效果,具有一定的工程应用价值.
| [1] | Petr K, Bogdan G, Sibylle S. Data-driven soft sensors in the process industry[J]. Computers and Chemical Engineering, 2009, 33(4): 795–814. DOI:10.1016/j.compchemeng.2008.12.012 |
| [2] | Petr K, Ratko G, Bogdan G. Review of adaptation mechanisms for data-driven soft sensors[J]. Computers and Chemical Engineering, 2011, 35(1): 1–24. DOI:10.1016/j.compchemeng.2010.07.034 |
| [3] |
宋坤, 李丽娟, 赵英凯.
基于PCA的仿射传播聚类算法[J]. 计算机工程与应用, 2011, 47(34): 212–214.
Song K, Li L J, Zhao Y K. Affinity propagation clustering algorithm based on principal components analysis[J]. Computer Engineering and Applications, 2011, 47(34): 212–214. DOI:10.3778/j.issn.1002-8331.2011.34.059 |
| [4] | He Y L, Xu Y, Geng Z Q, et al. Soft sensor of chemical processes with large numbers of input parameters using auto-associative hierarchical neural network[J]. Chinese Journal of Chemical Engineering, 2015, 23(1): 138–145. DOI:10.1016/j.cjche.2014.10.004 |
| [5] | Jin H P, Chen X G, Yang J W, et al. Multi-model adaptive soft sensor modeling method using local learning and online support vector regression for nonlinear time-variant batch processes[J]. Chemical Engineering Science, 2015, 131(1): 282–303. |
| [6] | Xiong W L, Zhang W, Xu B G, et al. JITL based MWGPR soft sensor for multi-mode process with dual-updating strategy[J]. Computers and Chemical Engineering, 2016, 90(1): 260–267. |
| [7] | Wang L, Zhang L, Han X, et al. An improved affinity propagation clustering algorithm based on principal component analysis and variation coefficient[J]. International Journal of Wireless and Mobile Computing, 2014, 7(6): 806–811. |
| [8] | Kaneko H, Funatsu K. Adaptive soft sensor based on online support vector regression and Bayesian ensemble learning for various states in chemical plants[J]. Chemometricsand Intelligent Laboratory Systems, 2014, 137(1): 57–66. |
| [9] | Grbić R, Slišković D, Kadlec P. Adaptive soft sensor for online prediction and process monitoring based on a mixture of Gaussian process models[J]. Computers and Chemical Engineering, 2013, 58(22): 84–97. |
| [10] |
朱群雄, 陈希, 贺彦林, 等.
基于PCA-DEA的乙烯装置能效分析[J]. 化工学报, 2015, 66(1): 278–283.
Zhu Q X, Chen X, He Y L, et al. Energy efficiency analysis for ethylene plant based on PCA-DEA[J]. Journal of Chemical Industry and Engineering, 2015, 66(1): 278–283. DOI:10.11949/j.issn.0438-1157.20141458 |
| [11] |
阮宏镁, 田学民, 王平.
基于联合互信息的动态软测量方法[J]. 化工学报, 2014, 65(11): 4497–4502.
Ruan H M, Tian X M, Wang P. Dynamic soft sensor method based on joint mutual information[J]. Journal of Chemical Industry and Engineering, 2014, 65(11): 4497–4502. DOI:10.3969/j.issn.0438-1157.2014.11.040 |
| [12] |
钱晓山, 阳春华, 徐丽莎.
基于改进差分进化和最小二乘支持向量机的铝酸钠溶液浓度软测量[J]. 化工学报, 2013, 64(5): 1704–1709.
Qian X S, Yang C H, Xu L S. Soft sensor of sodium aluminate solution concentration based on improved differential evolution algorithm and LSSVM[J]. Journal of Chemical Industry and Engineering, 2013, 64(5): 1704–1709. |
| [13] | Frey B J, Dueck D. Clustering by passing messages between data points[J]. Science, 2007, 315(5814): 972–976. DOI:10.1126/science.1136800 |
| [14] | Li X L, Su H Y, Chu J. Multiple model soft sensor based on affinity propagation, Gaussian process and Bayesian committee machine[J]. Chinese Journal of Chemical Engineering, 2009, 17(1): 95–99. DOI:10.1016/S1004-9541(09)60039-2 |
| [15] | Yang C, Bruzzone L, Guan R, et al. Incremental anddecremental affinity propagation for semisupervised clustering in multispectral images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(3): 1666–1679. DOI:10.1109/TGRS.2012.2206818 |
| [16] | Jin H P, Chen X G, Wang L, et al. Adaptive soft sensor development based on onlineensemble Gaussian process regression for nonlinear time-varying batch processes[J]. Industrial and Engineering Chemistry Research, 2015, 54(30): 7320–7345. DOI:10.1021/acs.iecr.5b01495 |
| [17] |
张伟, 熊伟丽, 徐保国.
基于实时学习的高斯过程回归多模型融合建模[J]. 信息与控制, 2015, 44(4): 487–492.
Zhang W, Xiong W L, Xu B G. Multi-model combination modeling based on just-in-time learning using Gaussian process regression[J]. Information and Control, 2015, 44(4): 487–492. |
| [18] |
何志昆, 刘光斌, 赵曦晶, 等.
高斯过程回归方法综述[J]. 控制与决策, 2013, 28(8): 1121–1137.
He Z K, Liu G B, Zhao X J, et al. Overview of Gaussian process regression[J]. Control and Decision, 2013, 28(8): 1121–1137. |
| [19] | Nguyen-Tuong D, Seeger M, Peters J. Model learning with local Gaussian process regression[J]. Advanced Robotics, 2009, 23(15): 2015–2034. DOI:10.1163/016918609X12529286896877 |
| [20] | Liu Y, Chen T, Chen J H. Auto-switch Gaussian process regression-based probabilistic soft sensors for industrial multigrade processes with transitions[J]. Industrial and Engineering Chemistry Research, 2015, 54(18): 5037–5047. DOI:10.1021/ie504185j |



