0 引言
区域物流系统作为物流业的基础设施,其建设已成为影响物流行业发展的重要因素,而区域物流系统的建设前提是精确的物流需求预测.对区域物流量进行研究与预测有助于把握区域物流的需求,实现区域物流供需相对平衡,对提高区域物流规划质量和运行效率具有重要的理论和实践意义.
目前区域物流需求预测已有较为丰富的研究成果.常用的方法可大致划分为两类:单一预测模型与组合预测模型.单一模型中比较有代表性的有:灰色预测模型[1]、线性回归预测模型[2-3]、时间序列预测模型[4-6]、神经网络预测模型[7-8]及支持向量机[2, 5, 9-10]等.灰色预测模型(GM(1,1))虽然可以通过累加生成新的数据序列,弱化原始数据的随机性,但其微分拟合过程相对比较粗糙,过程中容易遗失重要的信息,造成预测不够精确.线性回归操作简单,能快速找出各个影响因素之间的关联,但其对于数据的数量及质量均有较高的要求,在实际建模过程中存在一定困难.时间序列预测模型突出了时间因素在预测中的作用,当外界环境变化较大时,预测精度会受到严重的影响.神经网络存在收敛速度慢,计算复杂度髙,易陷于局部极小值等缺陷.
支持向量机(support vector machine,SVM)是基于VC维理论中的结构风险最小化原则,以统计学习理论为基础的一种新型机器学习算法.由于其在处理小样本、非线性和高维度的问题时具有较强优势,不少国内外学者将其应用到预测问题中[11-16].支持向量机模型的参数寻优问题是一个普遍性的难题,现阶段尚未有统一的方法可以很好地解决这一难题.目前常用的参数寻优方法包括遗传算法[11]和粒子群算法[12-14, 17-18].
组合预测通过对单一模型的组合,使每个模型在预测中发挥其各自的优势,从而提高预测精度.自组合预测理论提出以来已被广泛应用到各个领域[5-6, 19].随着现实问题的不断复杂化,要求模型解释问题的能力不断增强,多阶段模型被运用在很多预测问题中[20-21].综合考虑单阶段单一预测模型在预测时可能产生的过学习及算法收敛性问题,本文将基于支持向量机、遗传算法和粒子群算法分别建立GA-SVM预测模型和PSO-SVM预测模型,并借助BP神经网络监督式学习及强大的泛化映射能力,构建出两阶段组合预测模型GSPS-BPNN.通过成都市和天津市物流需求预测实例,证明了本文提出的两阶段组合预测模型GSPS-BPNN与其它单阶段单一预测模型相比在预测精度上具有较大优势.
1 GSPS-BPNN模型的构建 1.1 支持向量机回归原理支持向量机解决回归问题的思想[22]:假设训练样本集T={(xi,yi),i=1,2,…,Z},xi∈Rn,yi∈R,其中Z为训练的样本数,SVM期望寻找到一个从输入到输出的非线性映射,将数据映射到高维特征空间中,并在此特征空间用回归方程f(x)进行回归处理,f(x)可以定义如下:
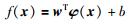
|
(1) |
式中,w表示权向量,b表示偏置量.目标为寻求w*和b*,在满足ε不敏感损失函数前提下最小化结构风险,同时引入松弛变量ξi、ξi*,则SVM待求解的优化问题为
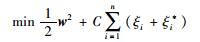
|
(2) |
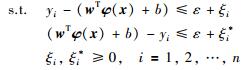
|
式中,C为惩罚参数,ξi、ξi*为非负松弛变量.根据KKT条件,引入拉格朗日乘子,将式(2)变为其对偶形式:
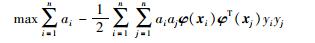
|
(3) |
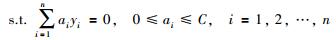
|
根据二次规划原问题与对偶问题解相同的性质,可得式(2)的最优解为a*=(a1*,a2*,…,an*)T,进而计算出w*和b*.最终得到回归表达式:
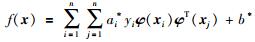
|
(4) |
式中,用核函数K(xi,xj)替代φ(xi) φT(xj),可以很好地避免数据的维数灾难.由于高斯核函数拥有更好的性能,后续实验选取高斯核函数作为预测模型的核函数,如式(5):
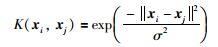
|
(5) |
遗传算法在解空间中搜索最优解时遵循优胜劣汰的自然法则,并且通过遗传操作可以保证解空间的多样性,使模型不易陷入局部最优解.GA-SVM模型的参数编码、适应度函数和遗传操作的设计为:
1) 参数编码设计
本文采用二进制方式对待优化参数(惩罚参数C、核函数参数σ)进行编码.考虑到区域物流需求预测问题中不同待优化参数的寻优范围不同,本文通过式(6)、式(7)计算得到相应的编码长度.
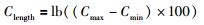
|
(6) |

|
(7) |
其中,Clength表示C的染色体编码长度,σlength表示σ的染色体编码长度.C及σ的染色体结构如图 1所示,其中各基因位为随机产生的二进制数.

|
| 图 1 编码方式 Figure 1 Coding mode |
2) 适应度函数设计
遗传算法在迭代寻优过程中不需要加入额外的先验知识,唯一引导求解方向的就是适应度函数.解的适应度越高,说明相应的区域物流需求真实值与预测值越接近.本文借助5折交叉验证的方法,通过样本均方误差(mean squared error,MSE)来评估区域物流需求真实值与模型预测值的差距.适应度函数如式(8)所示.
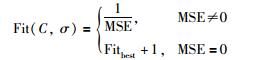
|
(8) |
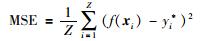
|
(9) |
其中,Fitbest为当前最优适应度,Z为样本数,f(xi)为预测值,yi*为真实值.
3) 遗传操作的设计
(1) 选择算子
选择过程主要是将优质的(C,σ)组合复制到下一代.本文采用轮盘赌法选择优质参数组合,即按照个体适应度在整个群体适应度中所占的比例,来确定该个体的被选择概率.
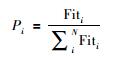
|
(10) |
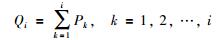
|
(11) |
其中,N为种群容量;Fiti为个体i的适应度;Pi为个体i被选择的概率;Qi为个体i的累计概率.累计概率和交叉率R∈(0,1)比较决定参与交叉的个体,如果R < Q1,就选第一个个体;否则选第i个个体,第i个个体满足Qi-1 < R < Qi.
(2) 交叉算子
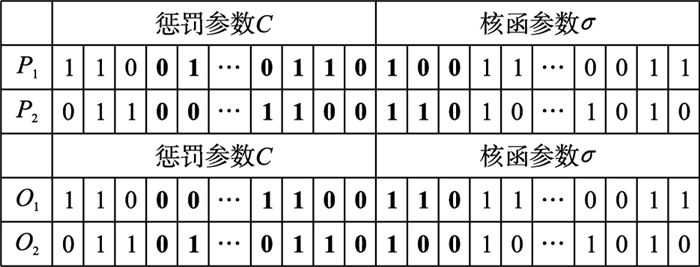
本文采用两点交叉作为模型的交叉算子,即随机选取个体上两个交叉点位,并将两个个体的两个交叉点位之间的部分进行交换,产生新的个体.具体操作如图 2,P1、P2表示亲代,O1、O2表示子代.
|
| 图 2 遗传算法交叉过程 Figure 2 Crossover process of the genetic algorithm |
(3) 变异算子
本文采用单点变异作为模型的变异算子,即在个体中随机指定变异位,然后将该变异位原始二进制数据进行取反处理.具体操作如图 3所示.

|
| 图 3 遗传算法变异过程 Figure 3 Variation process of the genetic algorithm |
第1阶段GA-SVM预测模型具体步骤如下:
① 确定遗传算法运行参数的大小,给出待优化参数(惩罚参数C、核函数参数σ)的取值范围[Cmin,Cmax]和[σmin,σmax];
② 建立20×(Clength+σlength)的矩阵作为种群,并随机生成二进制数,初始化种群;
③ 根据适应度函数式(8),计算出每组(C,σ)组合的适应度大小Fiti;
④ 根据式(10)、式(11)计算出每组(C,σ)组合的被选择的概率Pi及累计概率Qi.按照轮盘赌规则选择进行交叉变异的个体,并依据交叉率及变异率对其进行两点交叉及单点变异,从而获得新种群;
⑤ 当满足终止条件时(达到最大进化次数),停止计算;否则转到步骤c,直到结果满足终止条件;
⑥ 满足终止条件获得的输出就是最优参数组合(CGbest、σGbest),用最优SVM模型对数据样本进行预测,得出第一阶段预测的区域物流需求量R11={a1,a2,…,al}.
1.3 第1阶段PSO-SVM模型的构建粒子群算法参数寻优,将待优化参数(惩罚参数C、核函数参数σ)看作粒子,粒子的速度决定其运动的方向和距离,速度随自身及其它粒子的移动经验进行动态调整,从而实现惩罚参数C及核函数参数σ在解空间的寻优.在有N个粒子的种群中,假设k=1表示惩罚参数C,k=2表示核函数参数σ,用x(k)i=(x(k)i1,x(k)i2,…,x(k)iM)来表示粒子的当前位置,用v(k)i=(v(k)i1,v(k)i2,…,v(k)iM)表示粒子的飞行速度,用p(k)i=(p(k)i1,p(k)i2,…,p(k)iM)来表示当前粒子所搜寻到的最优位置,用g(k)i=(g(k)i1,g(k)i2,…,g(k)iM)表示整个粒子群所搜寻到的最优位置,即最优参数(C,σ)组合.粒子的位置和速度更新方程为
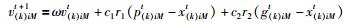
|
(12) |
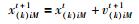
|
(13) |
其中,N表示粒子的数量,M表示搜索空间的维数,ω表示惯性因子,c1和c2分别表示局部学习因子和全局学习因子,r1和r2是[0, 1]的随机数,t为迭代次数.PSO算法的适应度函数设计与前文GA算法的适应度函数相似,但相对于GA算法的复杂遗传操作,PSO算法的操作步骤更加简便.第1阶段PSO-SVM预测模型具体实现步骤为:
1) 设置粒子群算法的运行参数,给出待优化参数(惩罚参数C、核函数参数σ)的取值范围,用[v(k)min,v(k)max]和[x(k)min,x(k)max]表示;
2) 初始化粒子种群中各个粒子的初始位置x(k)i及初始速度v(k)i;
3) 利用适应度函数式(8)计算出每个粒子的适应度,将每个粒子的最优位置p(k)i设置成该粒子的初始位置,从全部粒子中寻找最优位置设置成粒子群最优位置g(k)i;
4) 通过粒子速度及位置更新公式(式(12)、式(13))得到更新后的粒子群,利用式(8)计算更新后粒子的适应度,比较新粒子最优位置p(k)i及全局最优位置g(k)i,如果该粒子适应度优于之前计算得出的适应度,则更新p(k)i及g(k)i;否则保持原状;
5) 若满足终止条件(达到最大进化次数),停止计算;否则转到步骤4),直到结果满足终止条件;
6) 满足终止条件获得的输出就是最优参数组合(CPbest、σPbest),用最优SVM模型对数据样本进行预测,得出第1阶段预测的另一组区域物流需求量R12={b1,b2,…,bl}.
1.4 两阶段组合预测模型GSPS-BPNN的构建GSPS-BPNN模型的主要思想:通过两阶段组合预测弱化第1阶段预测模型(GA-SVM、PSO-SVM)可能产生的过学习的影响,并通过第1阶段预测捕捉到原始数据的数据特征,使第2阶段BPNN模型的输入数据维度大幅下降,进而解决了BPNN模型难于收敛的问题.
综合考虑神经网络的复杂度及计算成本,设置隐含层数为1层,隐含节点数为10个,则BPNN模型的输入层神经元、隐含层神经元和输出层神经元可以分别用式(14)~式(16)来表示:
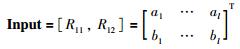
|
(14) |
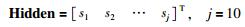
|
(15) |
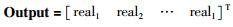
|
(16) |
BPNN模型完成由输入到输出的映射f : Rl→R,其隐含层各节点的输入为
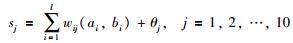
|
(17) |
式中,wij表示输入层到隐含层的连接权重,θj表示隐含层节点的阈值.BPNN模型的转移函数采用Sigmoid函数,则隐含层节点的输出为
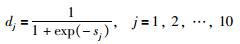
|
(18) |
同理,输出层的输入、输出为
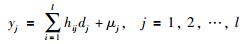
|
(19) |
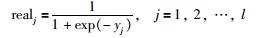
|
(20) |
式中,hij表示隐含层到输出层的连接权重;μj表示输出层节点的阈值.根据前文BPNN模型设计思路,构建第2阶段BPNN预测模型,具体实现步骤为:
1) 设置BPNN模型的运行参数;
2) 初始化各层连接权重(wij,hij)及阈值(θj,1);
3) 将第1阶段预测的两组区域物流需求量R11={a1,a2,…,al}及R12={b1,b2,…,bl}作为BPNN的输入神经元,实际区域物流需求量作为输出神经元,根据式(17)~式(20)进行模型训练;
4) 满足训练目标误差后,停止计算;获得各层连接权(wij*,hij*)及阈值(θj*,μj*),完成BPNN预测模型训练;
5) 使用训练好的BPNN预测模型对数据样本进行第2阶段预测,最终得到区域物流需求量.
综合前文的建模过程,构建出本文所提出的两阶段组合预测模型GSPS-BPNN的算法流程,如图 4所示.
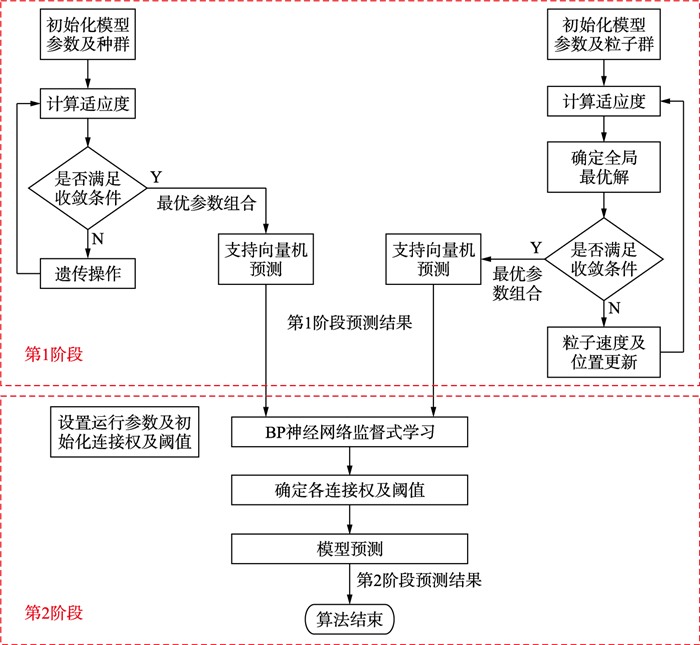
|
| 图 4 两阶段组合预测模型GSPS-BPNN流程图 Figure 4 The flow chart of two stage combination forecasting model GSPS-BPNN |
为验证所提出的GSPS-BPNN模型的有效性,本文以成都市和天津市1996年~2013年的数据作为预测的原始样本集(2015年数据尚未公布,2014年数据在年鉴中前后有差异).由于在实际应用中区域物流需求数据无法直接获得,通过对区域物流需求的影响因素分析,结果显示货运量可有效地反映出区域物流需求的变化趋势.因此本文以货运量作为本预测模型的决策变量.通过分析得出相应的影响指标体系,其具体统计数据如表 1和表 2所示(数据来源于成都市和天津市1996年~2013年统计年鉴).
| 年份 | 第一产业值/亿元 | 第二产业值/亿元 | 第三产业值/亿元 | 社会消费品零售总额/亿元 | 进出口贸易总额/亿美元 | 城市居民可支配收入/百元 | 农村居民可支配收入/百元 | 货运量/千万吨 |
| 1996 | 105.12 | 291.31 | 375.84 | 347.08 | 16.34 | 56.69 | 20.51 | 13.07 |
| 1997 | 108.94 | 324.86 | 441.69 | 409.99 | 12.32 | 60.19 | 24.27 | 14.34 |
| 1998 | 111.81 | 354.91 | 495.17 | 451.19 | 14.89 | 64.46 | 26.31 | 18.6 |
| 1999 | 112.15 | 383.79 | 548.96 | 500.08 | 16.13 | 70.98 | 27.83 | 19.63 |
| 2000 | 116.37 | 422.13 | 618.3 | 554.21 | 14.81 | 76.49 | 29.26 | 21.49 |
| 2001 | 118.49 | 490.3 | 713.27 | 627.52 | 18.95 | 81.28 | 31.78 | 23.72 |
| 2002 | 125.5 | 558.59 | 804.67 | 709.51 | 20.77 | 89.72 | 33.77 | 25.94 |
| 2003 | 137.05 | 652.45 | 915.77 | 776 | 25.17 | 96.41 | 36.55 | 28.8 |
| 2004 | 168.25 | 805.59 | 1 057.23 | 880.76 | 33.65 | 103.94 | 40.72 | 25.69 |
| 2005 | 177.15 | 984.19 | 1 214.65 | 1 005.88 | 45.36 | 113.59 | 44.85 | 26.7 |
| 2006 | 195.13 | 1 170.97 | 1 406.08 | 1 155.26 | 69.53 | 127.89 | 49.05 | 28.14 |
| 2007 | 235.1 | 1 444.08 | 1 685.61 | 1 357.2 | 95.16 | 148.49 | 56.42 | 30.03 |
| 2008 | 262.89 | 1 734.95 | 1 947.08 | 1 621.85 | 153.36 | 169.43 | 64.81 | 35.46 |
| 2009 | 267.77 | 2 001.8 | 2 233.04 | 2 047.21 | 178.63 | 186.59 | 71.29 | 39.54 |
| 2010 | 285.09 | 2 480.9 | 2 785.34 | 2 417.57 | 246.25 | 208.35 | 82.05 | 44.09 |
| 2011 | 327.34 | 3 143.82 | 3 479.42 | 2 861.28 | 379.06 | 239.32 | 98.95 | 34.37 |
| 2012 | 348.1 | 3 765.62 | 4 025.22 | 3 317.67 | 475.57 | 271.94 | 110.51 | 39.57 |
| 2013 | 353.17 | 4 181.49 | 4 574.23 | 3 991.18 | 505.85 | 299.68 | 129.85 | 43.33 |
| 年份 | 第一产业值/亿元 | 第二产业值/亿元 | 第三产业值/亿元 | 社会消费品零售总额/亿元 | 进出口贸易总额/亿美元 | 城市居民可支配收入/百元 | 农村居民可支配收入/百元 | 货运量/千万吨 |
| 1996 | 67.60 | 584.43 | 447.44 | 470.04 | 82.97 | 59.68 | 31.42 | 24.13 |
| 1997 | 69.43 | 643.88 | 521.97 | 535.02 | 100.23 | 66.09 | 35.48 | 25.09 |
| 1998 | 74.03 | 660.00 | 602.35 | 587.12 | 106.16 | 71.11 | 38.90 | 24.51 |
| 1999 | 71.01 | 711.93 | 667.12 | 657.28 | 126.05 | 76.50 | 40.55 | 27.05 |
| 2000 | 73.54 | 820.17 | 745.65 | 736.63 | 171.57 | 81.41 | 43.70 | 26.52 |
| 2001 | 78.55 | 904.64 | 856.91 | 832.70 | 181.86 | 89.59 | 48.25 | 28.23 |
| 2002 | 83.85 | 978.75 | 885.52 | 941.36 | 228.27 | 93.38 | 53.15 | 31.02 |
| 2003 | 89.70 | 1 212.34 | 1 084.90 | 922.27 | 293.71 | 103.13 | 58.61 | 35.25 |
| 2004 | 102.29 | 1 560.16 | 1 269.43 | 1 052.70 | 420.19 | 114.67 | 65.25 | 37.93 |
| 2005 | 109.42 | 2 050.34 | 1 504.10 | 1 190.06 | 533.87 | 126.39 | 72.02 | 40.26 |
| 2006 | 118.97 | 2 485.83 | 1 732.93 | 1 356.79 | 645.73 | 142.83 | 79.42 | 42.86 |
| 2007 | 102.86 | 2 891.33 | 2 024.09 | 1 603.74 | 715.50 | 163.57 | 87.52 | 51.34 |
| 2008 | 122.58 | 3 821.07 | 2 410.73 | 2 078.70 | 805.39 | 194.23 | 96.70 | 55.07 |
| 2009 | 131.01 | 4 110.54 | 3 259.25 | 2 430.83 | 639.44 | 214.02 | 106.75 | 43.55 |
| 2010 | 149.48 | 4 837.57 | 4 121.78 | 2 902.55 | 822.01 | 242.93 | 118.01 | 41.61 |
| 2011 | 159.09 | 5 878.02 | 5 153.88 | 3 395.06 | 1 033.91 | 269.21 | 118.91 | 44.65 |
| 2012 | 171.60 | 6 663.82 | 6 058.46 | 3 921.43 | 1 156.23 | 296.26 | 135.71 | 47.70 |
| 2013 | 188.45 | 7 276.68 | 6 905.03 | 4 470.43 | 1 285.28 | 326.58 | 154.05 | 51.60 |
本文所有实验均在操作系统为Windows 8,处理器为Core i5,主频为2.20 GHz,内存为8 G的PC上进行,主要编码实现工具为Matlab R2013a平台.
在第一阶段的预测中以1996年~2005年的数据作为训练集,2006年~2013年的数据作为测试集.经过多次重复实验,权衡预测精度和计算成本后,确定待优化参数(C,σ)的取值范围C∈[0.1,100],σ∈[0.01,1 000].GA-SVM的运行参数:种群容量为20,交叉率为0.5,变异率为0.05,最大迭代次数为100;PSO-SVM的运行参数:粒子群容量为20,最大迭代次数为100,局部学习因子为1.5,全局学习因子为2.为了减少随机搜索对解的稳定性的干扰,两种预测模型均取10次试验的平均预测结果.
第2阶段预测基于第1阶段所获得预测结果,以2006年~ 2010年预测数据作为训练集,2011年~2013年预测数据作为测试集.GSPS-BPNN的运行参数:最大迭代次数为20 000,训练目标误差0.001.与第1阶段预测类似,第2阶段预测结果取10次实验的平均结果.GSPS-BPNN预测模型的预测结果如下表 3和表 4所示.
| 年份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 平均值 | 相对误差/(%) |
| 2011 | 33.64 | 29.72 | 33.47 | 36.41 | 34.05 | 33.96 | 31.10 | 33.66 | 34.61 | 31.87 | 33.25 | -3.25 |
| 2012 | 46.58 | 42.28 | 44.66 | 44.96 | 35.08 | 46.65 | 41.75 | 40.98 | 35.74 | 29.89 | 40.86 | 3.26 |
| 2013 | 45.31 | 40.31 | 45.11 | 44.23 | 41.50 | 45.61 | 40.66 | 42.85 | 37.79 | 38.38 | 42.17 | -2.67 |
| 运算时间/s | 3.64 | 3.53 | 3.75 | 3.54 | 3.80 | 3.40 | 3.88 | 3.62 | 3.55 | 3.43 | 3.61 |
| 年份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 平均值 | 相对误差/(%) |
| 2011 | 44.54 | 50.45 | 40.06 | 48.00 | 42.14 | 33.07 | 34.03 | 43.78 | 48.27 | 49.87 | 43.42 | 2.75 |
| 2012 | 45.95 | 53.07 | 44.55 | 49.29 | 42.24 | 37.46 | 46.47 | 46.97 | 46.71 | 50.07 | 46.28 | 2.98 |
| 2013 | 46.11 | 56.46 | 45.16 | 49.29 | 43.77 | 48.92 | 50.31 | 47.58 | 46.10 | 52.84 | 48.65 | 5.71 |
| 运算时间/s | 4.18 | 5.82 | 3.63 | 4.23 | 3.72 | 3.81 | 3.78 | 4.29 | 4.15 | 3.96 | 4.16 |
从表 3和表 4可以看出,两阶段组合预测模型GSPS-BNPP对成都市及天津市2011年~2013年物流需求预测结果与真实值的相对误差分别在2%~4%和2%~6%之间且预测结果具有一定的稳定性.在实验过程当中,两阶段组合预测模型GSPS-BNPP的所有实验均在20 000次迭代内达到收敛要求(训练目标误差小于0.001),模型平均运算时间分别为3.61 s和4.16 s.为了突出两阶段组合预测模型的优势,本文采用单阶段GA-SVM预测模型、单阶段PSO-SVM预测模型和单阶段BPNN预测模型分别对该组数据进行了单独预测,形成对比实验,各个单阶段预测模型的预测结果见表 5~表 10.
| 年份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 平均值 | 相对误差/(%) |
| 2011 | 41.54 | 41.06 | 42.63 | 43.01 | 41.28 | 41.67 | 44.21 | 44.32 | 43.55 | 40.82 | 42.41 | 23.39 |
| 2012 | 42.29 | 42.82 | 44.93 | 45.48 | 42.06 | 44.01 | 44.61 | 44.81 | 46.11 | 41.39 | 43.85 | 10.82 |
| 2013 | 45.29 | 44.52 | 46.36 | 46.81 | 44.94 | 45.54 | 48.83 | 48.94 | 47.42 | 44.41 | 46.31 | 6.87 |
| 运算时间/s | 3.31 | 3.17 | 3.18 | 3.17 | 3.22 | 3.44 | 3.36 | 3.30 | 3.22 | 3.20 | 3.26 |
| 年份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 平均值 | 相对误差/(%) |
| 2011 | 42.75 | 40.70 | 42.81 | 40.51 | 41.27 | 42.81 | 40.68 | 40.80 | 40.72 | 40.98 | 41.40 | 7.27 |
| 2012 | 42.67 | 40.05 | 42.72 | 39.55 | 40.61 | 42.72 | 39.98 | 40.39 | 40.11 | 41.17 | 41.00 | 14.05 |
| 2013 | 42.06 | 38.97 | 42.09 | 38.21 | 39.74 | 42.09 | 38.85 | 39.55 | 39.07 | 40.09 | 40.07 | 22.34 |
| 运算时间/s | 2.96 | 3.00 | 2.88 | 2.99 | 2.96 | 3.18 | 2.89 | 2.97 | 2.99 | 2.90 | 2.97 |
| 年份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 平均值 | 相对误差/(%) |
| 2011 | 42.69 | 43.16 | 42.89 | 42.54 | 42.64 | 43.15 | 42.00 | 43.28 | 42.16 | 42.97 | 42.75 | 24.38 |
| 2012 | 45.21 | 45.68 | 45.30 | 44.54 | 45.16 | 45.73 | 44.38 | 45.80 | 44.53 | 45.52 | 45.18 | 14.19 |
| 2013 | 46.63 | 46.98 | 46.67 | 46.27 | 46.58 | 47.03 | 45.88 | 47.11 | 46.04 | 46.88 | 46.61 | 7.56 |
| 运算时间/s | 3.60 | 2.43 | 2.69 | 2.37 | 2.26 | 2.50 | 2.40 | 2.45 | 2.56 | 2.67 | 2.59 |
| 年份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 平均值 | 相对误差/(%) |
| 2011 | 40.52 | 40.68 | 40.71 | 40.73 | 42.82 | 40.73 | 40.72 | 40.85 | 40.86 | 40.70 | 40.93 | 8.33 |
| 2012 | 41.27 | 39.95 | 40.05 | 40.11 | 42.77 | 40.09 | 40.10 | 41.55 | 40.54 | 40.00 | 40.64 | 14.79 |
| 2013 | 42.66 | 38.77 | 38.93 | 39.02 | 42.20 | 38.98 | 39.01 | 42.66 | 39.80 | 38.84 | 40.09 | 22.31 |
| 运算时间/s | 1.93 | 2.16 | 1.84 | 1.87 | 1.92 | 1.96 | 1.87 | 1.86 | 1.90 | 1.94 | 1.93 |
| 年份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 平均值 | 相对误差/(%) |
| 2011 | 45.47 | 46.12 | 44.58 | 46.69 | 39.50 | 43.18 | 43.57 | 46.34 | 45.97 | 41.26 | 44.27 | 28.80 |
| 2012 | 45.23 | 46.11 | 46.00 | 46.96 | 37.98 | 42.70 | 47.59 | 46.46 | 47.55 | 42.70 | 44.93 | 13.54 |
| 2013 | 45.10 | 45.27 | 53.20 | 46.94 | 40.30 | 42.99 | 48.27 | 47.16 | 44.56 | 44.85 | 45.86 | 5.85 |
| 运算时间/s | 20.94 | 23.83 | 23.77 | 23.74 | 23.92 | 23.82 | 22.58 | 23.72 | 20.86 | 23.58 | 23.08 |
| 年份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 平均值 | 相对误差/(%) |
| 2011 | 42.62 | 41.68 | 43.83 | 40.24 | 44.75 | 40.31 | 42.28 | 36.26 | 35.12 | 35.59 | 40.27 | 9.81 |
| 2012 | 43.27 | 41.56 | 43.41 | 39.20 | 43.77 | 39.76 | 43.60 | 32.75 | 32.03 | 35.29 | 39.46 | 17.26 |
| 2013 | 43.83 | 41.58 | 42.69 | 38.96 | 42.09 | 40.00 | 44.05 | 31.10 | 31.29 | 35.95 | 39.15 | 24.12 |
| 运算时间/s | 22.71 | 22.37 | 22.45 | 22.47 | 22.51 | 22.11 | 22.63 | 22.43 | 23.42 | 22.50 | 22.56 |
根据表 5和表 6所示,单阶段GA-SVM预测模型的预测精度较低,且稳定性相对较差.成都实例中,预测结果最高相对误差达到23.39%,最低相对误差为6.87%,模型平均运算时间为3.26 s;天津实例中,最高相对误差为22.34%,最低相对误差7.27%,平均计算时间为2.97 s.
根据表 7和表 8所示,在成都实例及天津实例中,单阶段PSO-SVM预测模型的预测结果最大相对误差分别为24.38%和22.31%,最低相对误差分别为7.56%和8.33%,相对误差的跨度很大说明模型预测效果的稳定性有待提升.模型中粒子的并行操作,使模型的平均运算时间低至2.59 s和1.93 s.
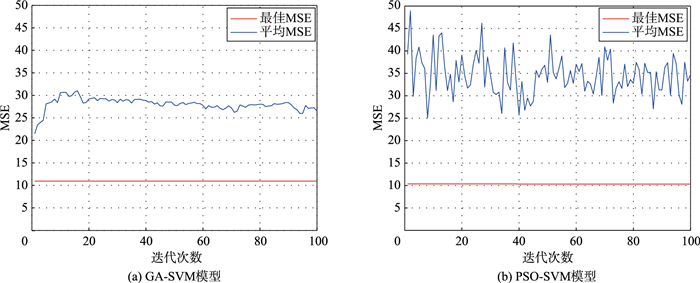
在第1阶段预测中,单阶段GA-SVM预测模型与单阶段PSO-SVM预测模型的相对误差及运算速度差异不大.两种进化算法在搜索最优解时寻优机制的不同,可以体现在模型的MSE分布中,如图 5和图 6所示.从平均MSE来看,两组实例中,GA算法在搜索解的过程中,解质量的变化差异不大,表现出比较平稳的趋势,但PSO算法在搜索解的过程中,解质量会出现相对更剧烈的波动,说明GA算法在一代解与另一代解之间的关联性要强于PSO算法.从最优MSE来看,两种算法均能较快地搜索到优质解,但GA算法能更快地搜索到最优解.成都实例中最优MSE在5以下,而天津实例中最优MSE在10左右,说明训练过程中成都实例中的最优解要优于天津实例中寻找到的最优解,但从预测结果来看,成都实例预测结果并没有优于天津实例,说明在训练过程中获得的最优解,不一定是测试集中的最优解.
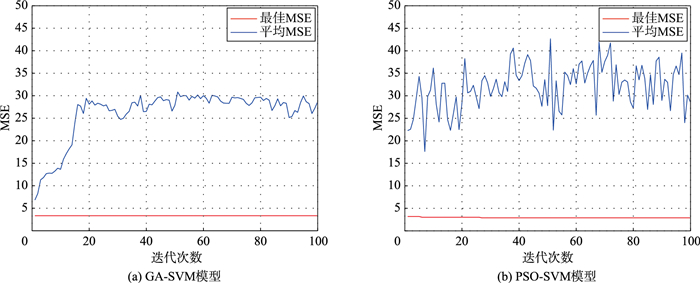
|
| 图 5 GA-SVM模型与PSO-SVM模型的MSE分布对比(成都) Figure 5 Comparison of MSE distribution between GA-SVM model and PSO-SVM model(Chengdu) |
|
| 图 6 GA-SVM模型与PSO-SVM模型的MSE分布对比(天津) Figure 6 Comparison of MSE distribution between GA-SVM model and PSO-SVM model(Tianjin) |
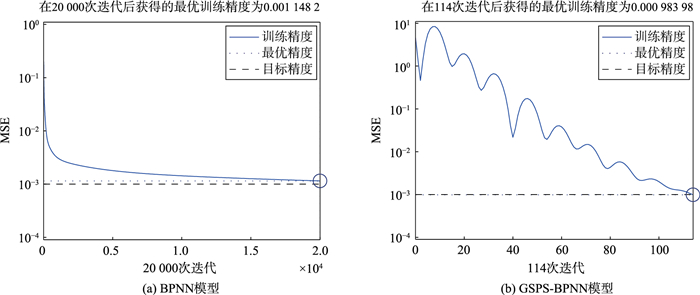
根据表 5所示,BPNN预测模型的预测稳定性是上述4种预测模型中最低的.成都实例中,最大相对误差高达28.80%,最低相对误差为5.85%;天津实例中,最大相对误差高达24.12%,最低相对误差为9.81%.在实验当中,BPNN模型在20 000次迭代中并没有达到算法的收敛要求(训练目标误差小于0.001),导致算法的运行时间高达23.08 s和22.56 s,说明了多维输入的神经网络模型会影响算法收敛性,从而增加模型的计算成本.图 6对比了BPNN模型(a)与GSPS-BPNN模型(b)的收敛效果,结果显示GSPS-BPNN模型能更快地达到算法收敛,有效地降低了计算成本.
|
| 图 7 GSPS-BPNN模型与BPNN模型的算法收敛对比 Figure 7 Comparison of algorithm convergence between GSPS-BPNN model and BPNN model |
为了更加全面地分析预测结果,引入绝对误差均值(mean absolute error,MAE),绝对百分比误差均值(mean absolute percentage error,MAPE)两项衡量指标,MAE和MAPE值越小,说明模型预测效果越优秀.
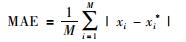
|
(21) |
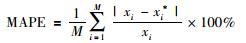
|
(22) |
其中,M为测试集样本数,xi为真实值,xi*为预测值.
从表 11可以看出,在两组实例中,两阶段GSPS-BPNN模型的两项衡量指标MAE及MAPE都处于同组最低,说明两阶段GSPS-BPNN模型的预测效果优于其它3种单阶段的预测模型.
| 算法 | 成都实例 | 天津实例 | ||
| MAE | MAPE | MAE | MAPE | |
| GA-SVM | 5.10 | 13.69% | 7.16 | 14.55% |
| PSO-SVM | 5.76 | 15.38% | 7.43 | 15.14% |
| BPNN | 5.93 | 16.06% | 8.35 | 17.07% |
| GSPS-BPNN | 1.19 | 3.06% | 1.87 | 3.81% |
综上所述,4种模型的预测结果在一定程度上存在着差异.从预测精度的角度看,两阶段GSPS-BPNN模型的预测结果相对误差在2%~6%之间,要优于单阶段GA-SVM、单阶段PSO-SVM及单阶段BPNN模型;从运算时间来看,两阶段GSPS-BPNN模型,单阶段GA-SVM模型及单阶段PSO-SVM模型的运算时间较为接近,而单阶段BPNN预测模型计算成本较高;从预测结果的稳定性来看,两阶段GSPS-BPNN模型要优于其它3种单阶段预测模型.图 8和图 9能更加直观地反映出4种预测方法在两组实例中的预测精度.
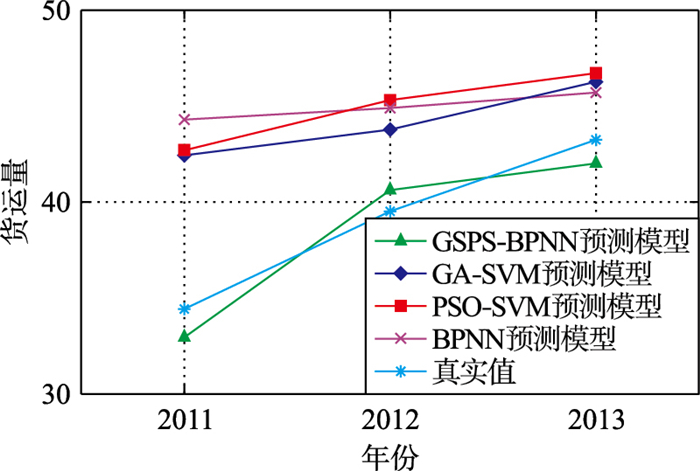
|
| 图 8 4种预测模型预测结果与真实值对比(成都) Figure 8 Comparison among four kinds of prediction model and real value (Chengu) |
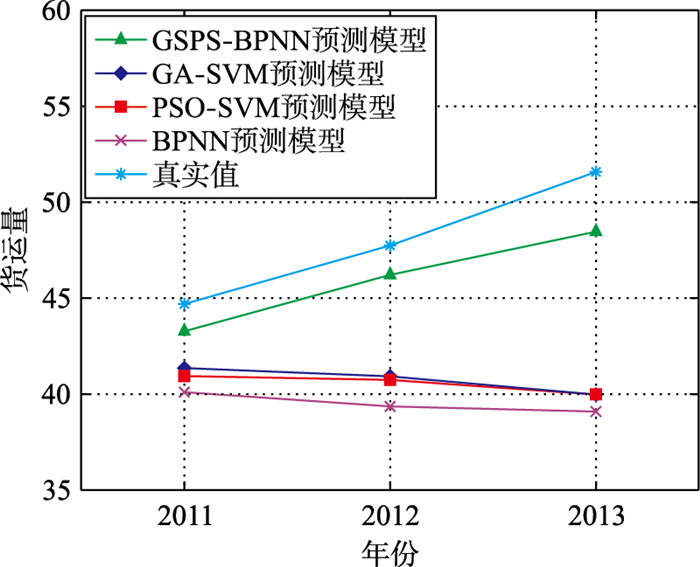
|
| 图 9 4种预测模型预测结果与真实值对比(天津) Figure 9 Comparison among four kinds of prediction model and real value (Tianjin) |
本文基于GA、PSO及BPNN构建了两阶段区域物流需求组合预测模型GSPS-BPNN,分别在预测精度、预测稳定性及计算成本三个方面与单一的单阶段预测模型进行了对比,研究结果表明GSPS-BPNN模型具有较明显的优势,预测精度均超过94%且具有一定的稳定性,计算成本相对较低.
GSPS-BPNN作为一种两阶段预测模型,与单阶段预测模型(GA-SVM模型、PSO-SVM模型及BPNN模型)的本质区别在于两阶段预测模型是在预测结果上再次进行预测,是一种二次加工,而单阶段预测模型仅仅基于条件属性直接进行预测.实验结果表明在特定问题中两阶段预测具有一定优势,原因在于两阶段预测模型中的第1阶段预测能够减弱原始样本数据中的噪声信息,获取更多反映数据内在关联及变化趋势的数据特征信息,并将这些特征信息映射到第1阶段预测结果中,使第2阶段的预测建立在具有更多有效特征信息数据集的基础之上.并且GSPS-BPNN模型避免了算法过学习现象及收敛性问题.寻找最佳模型搭配组合,及如何获得数据训练集与测试集最佳分界点将成为下一阶段的研究重点.
| [1] |
邹欣, 张梦芩.
基于灰色GM(1, 1)模型的四川省物流需求预测[J]. 物流技术, 2015(9): 166–169.
Zou X, Zhang M C. Forecasting of logistics demand of sichuan based on GM(1, 1)[J]. Logistics Technology, 2015(9): 166–169. |
| [2] |
张奇, 胡蓝艺, 王珏.
基于Logit与SVM的银行业信用风险预警模型研究[J]. 系统工程理论与实践, 2015(7): 1784–1790.
Zhang Q, Hu L Y, Wang J. Study on credit risk early warning based on logit and SVM[J]. System Engineering-Theory and Practice, 2015(7): 1784–1790. DOI:10.12011/1000-6788(2015)7-1784 |
| [3] |
刘宇, 吴迎学, 党文峰.
基于多元线性回归的区域物流需求预测研究[J]. 物流工程与管理, 2014(3): 52–54.
Liu Y, Wu Y X, Dang W F. Regional logistics demand forecasting based on multiple linear regression[J]. Logistics Engineering and Management, 2014(3): 52–54. |
| [4] |
曾鸣, 程文明, 林磊.
状态空间时间序列的区域物流需求预测研究[J]. 计算机工程与应用, 2014, 50(15): 7–12.
Zeng M, Cheng W M, Lin L. Research of regional logistics demand forecasting using state space timeseries[J]. Computer Engineering and Applications, 2014, 50(15): 7–12. DOI:10.3778/j.issn.1002-8331.1311-0075 |
| [5] |
李琨, 韩莹, 黄海礁.
基于IBH-LSSVM的混沌时间序列预测及其在抽油井动液面短期预测中的应用[J]. 信息与控制, 2016, 45(2): 241–247.
Li K, Han Y, Huang H J. Chaotic time series prediction based on IBH-LSSVM and its application to short-term prediction of dynamic fluid level in oil wells[J]. Information and Control, 2016, 45(2): 241–247. |
| [6] |
田中大, 李树江, 王艳红, 等.
基于ARIMA补偿ELM的网络流量预测方法[J]. 信息与控制, 2014, 43(6): 705–710.
Tian Z D, Li S J, Wang Y H, et al. Network traffic prediction method based on extreme learning machinewith ARIMAcompensation[J]. Information and Control, 2014, 43(6): 705–710. |
| [7] |
李哲敏, 许世卫, 崔利国, 等.
基于动态混沌神经网络的预测研究——以马铃薯时间序列价格为例[J]. 系统工程理论与实践, 2015, 35(8): 2083–2091.
Li Z M, Xu S W, Cui L G, et al. Prediction study based on dynamic chaotic neural network-Taking potato time-series prices as an example[J]. System Engineering Theory and Practice, 2015, 35(8): 2083–2091. DOI:10.12011/1000-6788(2015)8-2083 |
| [8] |
李军, 黄杰.
基于自组织映射神经网络的局部自回归方法在网络流量预测中的应用[J]. 信息与控制, 2016, 45(1): 120–128.
Li J, Huang J. Prediction of network traffic using local auto-regression methods based on self-organizing map neural network[J]. Information and Control, 2016, 45(1): 120–128. |
| [9] | Ahn J J, Oh K J, Kim T Y, et al. Usefulness of support vector machine to develop an early warning system for financial crisis[J]. Expert Systems with Applications, 2011, 38(4): 2966–2973. DOI:10.1016/j.eswa.2010.08.085 |
| [10] | Yu L, Yue W, Wang S, et al. Support vector machine based multiagent ensemble learning for credit risk evaluation[J]. Expert Systems with Applications, 2010, 37(2): 1351–1360. DOI:10.1016/j.eswa.2009.06.083 |
| [11] | Guo X, Li D C, Zhang A. Improved support vector machine oil price forecast model based on genetic algorithm optimization parameters[J]. Aasri Procedia, 2012, 1(4): 525–530. |
| [12] |
陈荣, 梁昌勇, 陆文星, 等.
基于季节SVR-PSO的旅游客流量预测模型研究[J]. 系统工程理论与实践, 2014(5): 1290–1296.
Chen R, Liang C Y, Lu W X, et al. Forecasting tourism flow based on seasonal PSO-SVR model[J]. System Engineering Theory and Practice, 2014(5): 1290–1296. DOI:10.12011/1000-6788(2014)5-1290 |
| [13] | Wang X, Wen J, Zhang Y, et al. Real estate price forecasting based on SVM optimized by PSO[J]. Optik-International Journal for Light and Electron Optics, 2014, 125(125): 1439–1443. |
| [14] | Selakov A, Cvijetinović D, Milović L, et al. Hybrid PSO-SVM method for short-term load forecasting during periods with significant temperature variations in city of Burbank[J]. Applied Soft Computing, 2014, 16(3): 80–88. |
| [15] | Kisi O, Parmar K S. Application of least square support vector machine and multivariate adaptive regression spline models in long term prediction of river water pollution[J]. Journal of Hydrology, 2016, 534: 104–112. DOI:10.1016/j.jhydrol.2015.12.014 |
| [16] |
张贵生, 张信东.
基于近邻互信息的SVM-GARCH股票价格预测模型研究[J]. 中国管理科学, 2016, 24(9): 11–20.
Zhang G S, Zhang X D. Research on SVM-GARCH stock price forecasting model based on nearest neighbor mutual information[J]. Chinese Journal of Management Science, 2016, 24(9): 11–20. |
| [17] | Yang Q, Zou H Y, Zhang Y, et al. Multiplex protein pattern unmixing using a non-linear variable-weighted support vector machine as optimized by a particle swarm optimization algorithm[J]. Talanta, 2016, 147: 609–614. DOI:10.1016/j.talanta.2015.10.047 |
| [18] |
王通, 高宪文, 翟瑀佳, 等.
基于PSO-LSSVM预测的改进传感器故障检测和隔离[J]. 信息与控制, 2014, 43(2): 146–151.
Wang T, Gao X W, Zhai Y J, et al. Improved detection and isolation of sensor fault based on PSO-LSSVM prediction[J]. Information and Control, 2014, 43(2): 146–151. |
| [19] | Buhan S, Cadirci I. Multistage wind-electric power forecast by using a combination of advanced statistical methods[J]. IEEE Transactions on Industrial Informatics, 2015, 11(5): 1–1. DOI:10.1109/TII.2015.2475695 |
| [20] | Zou H F, Xia G P, Yang F T, et al. A neural network model based on the multi-stage optimization approach for short-term food price forecasting in China[J]. Expert Systems with Applications, 2007, 33(2): 347–356. DOI:10.1016/j.eswa.2006.05.021 |
| [21] | Huang C J, Chen P W, Pan W T. Using multi-stage data mining technique to build forecast model for Taiwan stocks[J]. Neural Computing and Applications, 2012, 21(8): 2057–2063. DOI:10.1007/s00521-011-0628-0 |
| [22] | Vapnik V N. The nature of statistical learning theory[J]. IEEE Transactions on Neural Networks, 1995, 10(5): 988–999. |



