2. 空军航空大学, 吉林 长春 130022
2. Aviation University of Air Force, Changchun 130022, China
0 引言
随着人工智能的发展,群系统的编队控制问题受到了国内外研究者的大量关注,并在很多领域得到了广泛的应用[1-2],例如多机器人编队控制、多无人机编队控制、以及多卫星的编队控制等.传统编队控制方法主要有:领导者—跟随者方法、基于虚拟结构的方法以及基于行为的方法.
尽管上述3种方法可以用来解决群系统的编队控制问题,但也存在着一些不足之处,例如:鲁棒性较差,不适用于分布式结构,通信代价较大等.近年来,随着多智能体一致性理论的发展,越来越多的学者发现,可以用一致性理论来解决群系统的编队控制问题.文[3]关注大规模群系统,利用一致性理论,提出了一种有限时间编队控制方法.文[4]中传统的一致性方法扩展后被应用于二阶动态系统的编队控制中;文[5]将该方法应用于多机器人平台的编队控制中,并对实验结果进行了分析和讨论. Seo在文[6]中提出了一种基于一致性的输出反馈方法,解决了时变参考编队下多无人机群系统的队形控制问题.文[7]研究了基于一致性策略的二阶无人机群系统时变编队控制方法,给出了编队形成的充要条件,并进行了室外飞行试验.文[8]提出了一种自适应增益调节技术,研究群系统的时变编队控制问题.文[9]根据船舶的通信需求和作业模式,提出了一种船舶协同编队控制方法,实现了任务驱动的船舶协同编队控制.
文[3-9]的研究均是针对通信条件无约束的理想情况,但在实际的编队控制中,群系统中各主体之间的通信可能会受到限制,因此需要考虑如时间延迟、通信拓扑切换等复杂通信条件对编队产生的影响.文[10]对二阶群系统进行了研究,并通过引入自身时延,提出了时延条件下的编队控制方法.文[11]研究了二阶群系统在位置时延和速度时延条件下的编队控制问题.上述文献中,只是讨论了时延对编队形成产生的影响,并没有给出群系统允许的时延上界. Qin在文[12]中研究了常数时延条件下的二阶群系统编队控制问题. Abdelkader考虑时变时延问题,通过构造Lyapunov-Krasovskii泛函,研究定常/时变时延下的多无人机群系统的编队问题[13].文[14]给出了高阶群系统在时延情况下形成编队的充要条件.文[15]研究时变时延下的高阶线性群系统编队控制问题,并给出了保守性较小的时延上界.
在切换通信拓扑方面,文[16]研究了二阶无人机群系统在无向切换拓扑条件下的编队控制问题,并进行了数值仿真及实际飞行实验.文[17]针对有向切换拓扑约束条件,研究了多无人机编队控制问题,通过引入平均驻留时间来解决切换拓扑对编队产生的影响. Dong在文[18]中对高阶群系统在无向切换拓扑条件下的编队控制问题进行了研究.文[19]利用自适应输出反馈方法,研究了切换拓扑条件下的群系统编队控制问题.文[20]研究了无向切换拓扑和固定时延条件下的多飞行器编队控制问题.
从现有的研究成果来看,已有一些文献针对复杂通信条件下的群系统编队问题进行研究,但多数只是针对通信时延和切换通信拓扑其中的一个条件进行讨论[10-19],考虑这两个复杂通信条件同时存在的文献较少[20].对于通信时延,文[10-12, 20]都假设时延是固定的;而切换通信拓扑方面,文[16, 18, 20]均假设主体之间的通信是双向的,即无向通信拓扑.
本文主要研究了基于自由权矩阵方法的线性群系统编队控制问题.与已有的研究成果相比,本文的主要贡献有:1)针对时变时延和有向切换拓扑两个复杂通信条件同时存在的情况,研究线性群系统的编队控制问题.本文考虑的通信条件与现有文献相比更加复杂;2)适用于大规模群系统.文[15-16]中给出的LMI判据中都存在Kronecker乘积项,当群系统规模增大时,其计算复杂度也会随之增加.而在本文中,最多只需要考虑4个维数较低的LMI判据,因此更适用于大规模群系统的编队控制;3)得到了理论的时延上界.为了降低计算时延上界时的保守性,采用自由权矩阵方法,分析群系统的编队控制问题,得到了系统允许的时延上界.在之前的工作中,文[21-22]研究了时变时延群系统平均一致性问题,通过引入自由权矩阵,得到了保守性较低的时延稳定性判据.
文中R>(<)0表示矩阵R是正定(负定)的,符号ⓧ为笛卡尔乘积.矩阵中*表示对称项.对于任意的复数向量x、实数矩阵X和任意的λ∈C,定义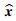
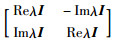
引理1[23] 图G的拉普拉斯矩阵L至少有一个0特征值且1是0特征值所对应的右特征向量,即L1=0.如果图G是一个有向图且含有一个有向生成树(至少存在一个节点到其它所有节点都有一条有向路径),则0是L的单特征值,其余的非零特征值均具有正实部.
引理2[24] 如果矩阵Y∈RN×N的各行和均为零,则存在矩阵Z∈RN×(N-1)和矩阵E∈R(N-1)×N使得Y=ZE,E的定义如下:
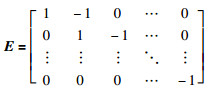
|
如果0是矩阵Y的单特征值,那么矩阵Z是列满秩的.
引理3(Schur补引理)[25] 对给定的对称矩阵S=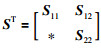
1) S<0;
2) S11<0,S22-S12TS11-1S12<0;
3) S22<0,S11-S12S22-1S12T<0.
引理4[26] 存在对称矩阵X,使得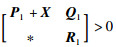
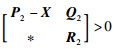
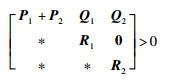
|
引理5[27] 对矩阵A∈Rm×n和矩阵B∈Rn×m(n≥m),二者乘积满足如下性质:
1) 若λ是矩阵AB的特征值,则λ也是矩阵BA的特征值.
2) 若λ≠0是矩阵BA的特征值,则λ也是矩阵AB的特征值.
3) 若λ1,λ2,…,λm是矩阵AB的特征值,则矩阵BA的n个特征值为λ1,λ2,…,λm,0,…,0.
2 问题描述及编队控制协议 2.1 问题描述考虑由N个主体组成的线性群系统:
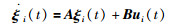
|
(1) |
其中,i=1,2,…,N,A为系统矩阵. ξi(t)∈Rn是第i个主体的状态,ui(t)∈Rm是第i个主体的控制输入.假设输入矩阵B是列满秩矩阵,各主体之间的通信用有向图G表示且图G具有一个生成树. B是列满秩矩阵,由矩阵知识可知,存在一个非奇异矩阵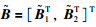
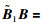
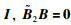
用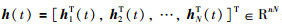
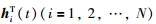
定义1 对于群系统(1),如果存在一个向量函数r(t)∈Rn使得
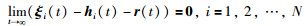
|
(2) |
则称群系统(1)能够形成时变编队h(t),其中r(t)为编队参考函数,可以用来表示编队中心的运动模态.
2.2 编队控制协议基于一致性理论,考虑存在时延的状态编队控制协议:
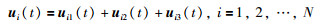
|
(3) |
其中,
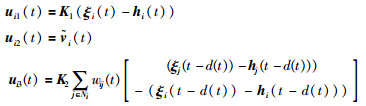
|
Ni表示第i个主体的邻居集合,控制器增益K1和K2,分别是具有匹配维数的常数矩阵. 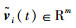
考虑存在通信拓扑切换约束,令M={G1,G2,…,Gs},s≥1表示所有可能的通信拓扑组成的集合. σ(t):[0,+∞)→S={1,2,…,s}表示通信拓扑的切换信号,其在时刻t的取值表示通信拓扑图Gσ(t)对应M中元素的下标.与Gσ(t)对应的拉普拉斯矩阵为Lσ(t).
3 编队控制协议设计 3.1 充分必要条件根据定义1,下面的定理1给出了群系统(1)实现编队的充要条件.
定理1 对于任意给定的有界初始条件,群系统(1)在时变时延和切换拓扑条件下,通过ui(t)的控制可以形成时变编队h(t)的充要条件是:
Ⅰ)对于矩阵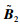
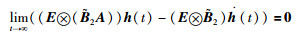
|
(4) |
Ⅱ)对于矩阵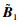
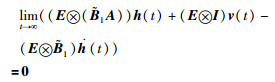
|
(5) |
Ⅲ)对于所有的切换信号σ(t),N-1个子系统是渐近稳定的:
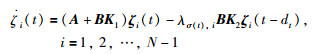
|
(6) |
证明 将式(3)代入式(1),并令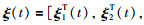
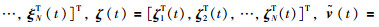
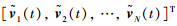
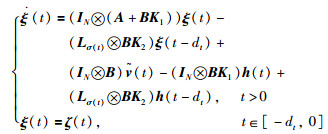
|
(7) |
其中,Lσ(t)为拓扑连通图的拉普拉斯矩阵.
令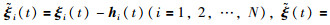
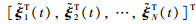
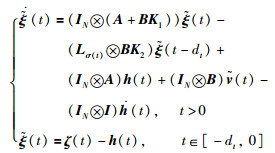
|
(8) |
根据定义1,如果式(8)中各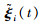
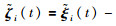
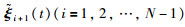
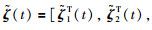
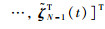
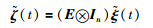
|
(9) |
其中,E由引理2给出.
由引理1和引理2可知,存在列满秩矩阵Zσ(t)∈RN×(N-1),使得Lσ(t)=Zσ(t)E,对式(9)求导可得
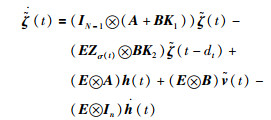
|
(10) |
其中,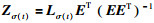
对于矩阵EZσ(t),存在非奇异矩阵Uσ(t)=[u1σ(t),u2σ(t),…,uN-1σ(t)],使得Uσ(t)-1EZσ(t)Uσ(t)=Jσ(t),其中Jσ(t)是矩阵EZσ(t)的Jordan标准型.对于所有的σ(t),令ζ(t)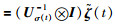
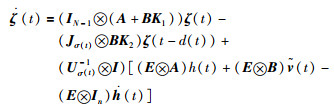
|
(11) |
如果变量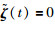
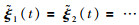
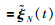
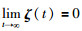
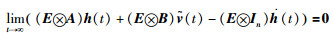
|
(12) |
且条件(Ⅲ)成立时,群系统(1)在时变时延和切换拓扑约束下可以形成编队h(t).
对式(12)两端同时乘以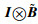
注1 式(6)中的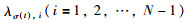
注2 控制协议中的ui1(t)不包含dt,可参照文[13]中的方法对ui1(t)进行设计,即通过配置状态编队参考r(t)的运动模态,设计控制器增益K1.
注3 对于条件(Ⅰ),其中不包含控制协议(3)中的控制量,即群系统若要形成编队h(t),自身动态特性需要满足式(4).对于ui2(t)中的辅助函数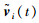
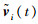
下面主要讨论控制器增益K2和时延dt上界的求解方法.
3.2 时延系统镇定分析控制器增益K1的求解方法由注2给出,因此需要考虑如何选取控制器增益K2使系统镇定.令A0K=A+BK1,时延dt满足0≤dt≤h且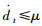
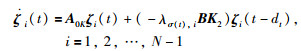
|
(13) |
下面的定理2给出了时延系统(13)镇定的条件.
定理2 对于所有的σ(t),若存在适当维数的实矩阵P>0,Q>0,R>0,Vk以及常数a和b(b≠0),使得:
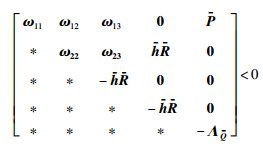
|
(14) |
其中,
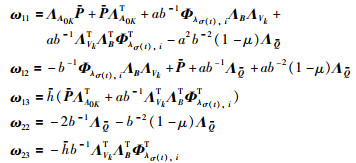
|
则闭环时延系统(13)渐近稳定且控制器增益为K2=VkQ-1.
证明 考虑通信拓扑图为有向图,其对应的拉普拉斯矩阵的特征值存在实部和虚部.因此,利用实部、虚部分解的方法,式(13)等价于系统:
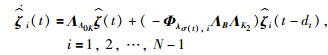
|
(15) |
利用牛顿—莱布尼茨公式,对于矩阵M1和M2,有:
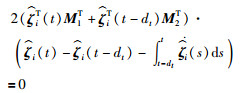
|
(16) |
另一方面,对于任意合适维数的矩阵Xmn(m=1,2;m≤n≤2),有:
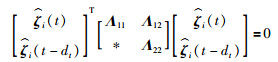
|
(17) |
其中,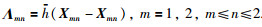
构造公共Lyapunov-Krasovskii泛函:
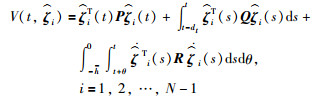
|
(18) |
式中,P=PT>0,Q=QT≥0,R=RT>0.
对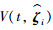
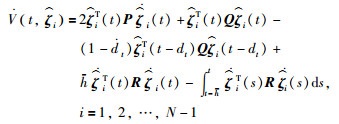
|
(19) |
将式(16)和式(17)加到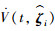
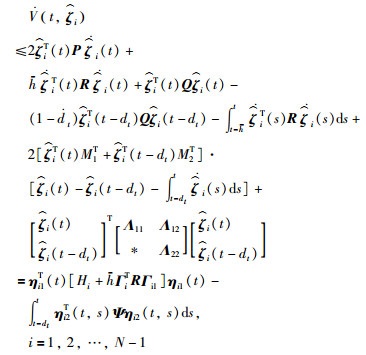
|
(20) |
其中,
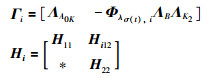
|
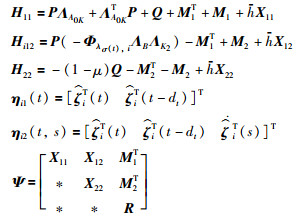
|
由Lyapunov-Krasovskii稳定性定理可知,在式(20)中,对于所有的σ(t),如果:
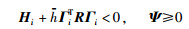
|
(21) |
成立,则闭环系统(13)是渐近稳定的.
由引理3:
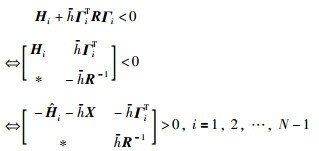
|
(22) |
式中,
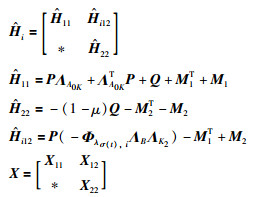
|
如果式(21)对严格不等号成立,则:
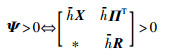
|
(23) |
式中,Π=[M1 M2].
由引理4,式(22)与式(23)同时成立,当且仅当:
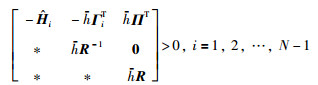
|
(24) |
而式(24)等价于式(25):
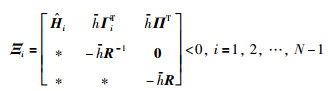
|
(25) |
则可知若式(25)成立,则式(21)一定成立.由Lyapunov-Krasovskii稳定性定理,若式(25)成立,则闭环系统(13)是渐近稳定的.
由于式(25)中存在非线性项,为求解控制器增益K2,需要对式(25)做进一步处理.为此,定义:
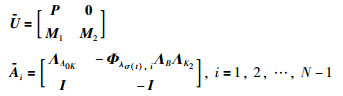
|
那么,就有:
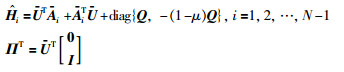
|
令M1=aP,M2=bQ,其中b≠0.此时U是可逆的,且:
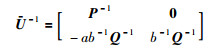
|
(26) |
定义矩阵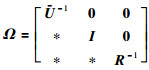
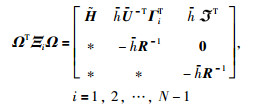
|
(27) |
式中,
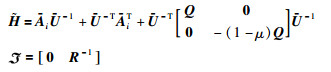
|
将式(26)代入式(27),并令P=P-1,R=R-1,ΛQ=Q-1以及Vk=K2Q,经过运算之后可以得到:
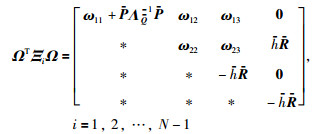
|
(28) |
其中ωij定义于式(14).如果LMI(14)成立,则由引理3就有ΩTΞiΩ<0也成立,于是Ξi<0,从而,若存在适当维数的实矩阵P>0,Q>0,R>0以及Vk,闭环系统(13)在控制器增益K2=VkQ-1的作用下是渐近稳定的.证毕.
注4 根据定理2,借助Matlab工具箱中的优化算法和LMI的feasp求解器进行迭代计算,可以得到系统允许的最大时延上界h和参数a、b.
注5 若定理2中的σ(t)为一个固定值,则群系统中,各主体之间的拓扑图变为非切换的固定拓扑,因此定理2同样适用于固定拓扑下的群系统编队控制.
注6 对于控制器增益K2和时延上界h,可以通过求解式(14)得到.实际上,对于定理2中的矩阵Φλσ(t),i(i=1,2,…,N-1),并不需要针对所有的σ(t)都进行计算.对于有向图而言,只需要考虑Φλi(i=1,2,3,4)四个矩阵即可,其中λi(i=1,2,3,4)定义为:
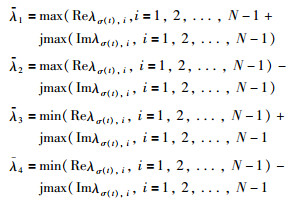
|
当群系统规模较大时,这种处理方法可以在很大程度上减少计算量[28].而在文[15-16]中,得到的LMI判据维数,会随着群系统中主体数量的增加而增大,从而增加了计算的复杂度.因此,本文的方法更适合于大规模群系统的编队控制.
4 数值仿真与分析为了验证群系统编队控制方法的有效性,采用二阶积分器表述的无人机运动模型[14, 20-21].由注6可知,即使群系统中主体个数很多,本文方法也只需考虑4个LMI判据.因此,考虑包含8架无人机的编队控制问题.编队在二维平面上运动,图 1给出了各无人机之间可能的3种通信拓扑图.

|
| 图 1 通信拓扑图 Figure 1 Interaction topology G |
每架无人机可以利用式(1)描述,其中,
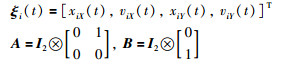
|
ξi(t)中的4个变量,分别表示X和Y方向的位置和速度.定义编队为
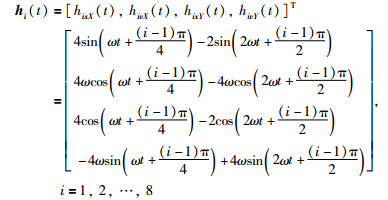
|
其中,ω=0.35 rad/s. 8架无人机实现编队h(t)后,会在二维平面内沿着一个心形线轨迹以0.35 rad/s的速度运动.由注3可以得到辅助函数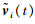
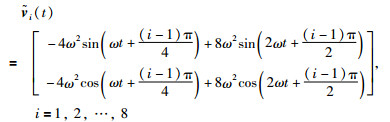
|
由注2可知,K1可以配置编队中心r(t)的运动模态.选取K1=I2ⓧ[-2.5,-1.5],将A+BK1的极点配置在-0.75+1.3919j和-0.75-1.3919j(其中j2=-1),此时编队中心r(t)是静止不动的.根据定理2,可以得到系统允许的时延上界为2.40 s,利用求得的参数a、b,还可以求解出不同时延下的控制器增益K2.当时变时延为1.6+0.8sint·s时,得到的控制器增益K2=I2ⓧ[-0.005 3,0.016 6].
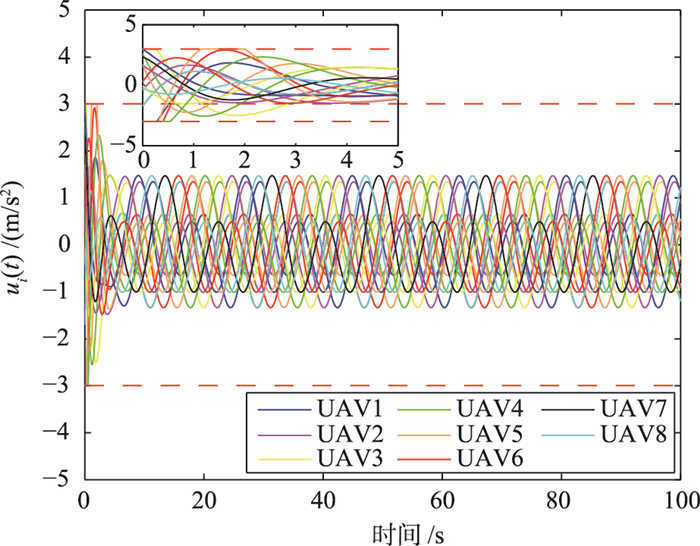
对于二阶积分器表述的无人机模型,其编队控制输入即为无人机的加速度输入.考虑到无人机自身的限制,将编队控制输入限制在±3 m/s2之间,图 2给出了每架无人机的编队控制输入曲线及其局部放大图.从图中可以看出,在初始的调整阶段,会发生输入值超过限制值的情况.进行输入限幅之后,在起始阶段,超过±3 m/s2范围的输入被限制在±3 m/s2之间.经过一段时间之后,无人机编队形成且趋于稳定,编队控制输入保持在一定的范围内变化.
|
| 图 2 编队控制输入 Figure 2 Inputs of the formation control |
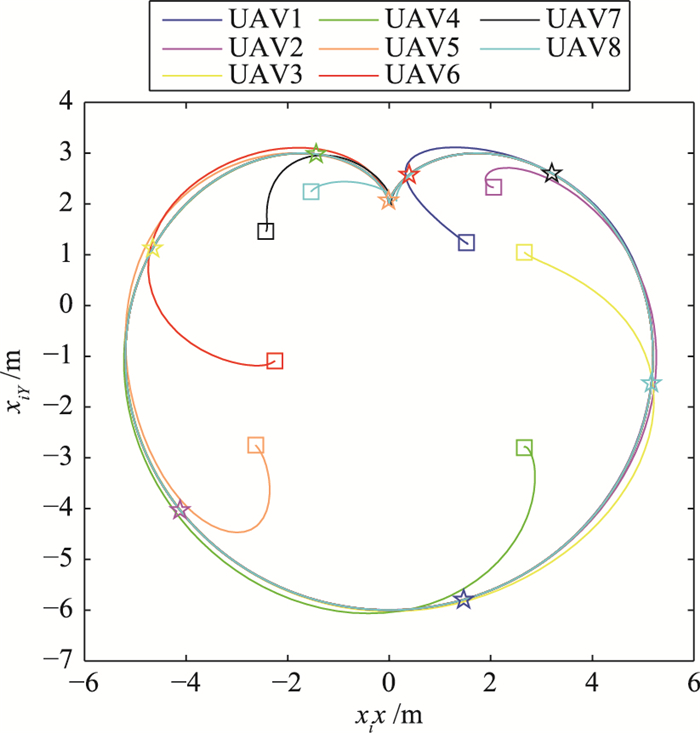
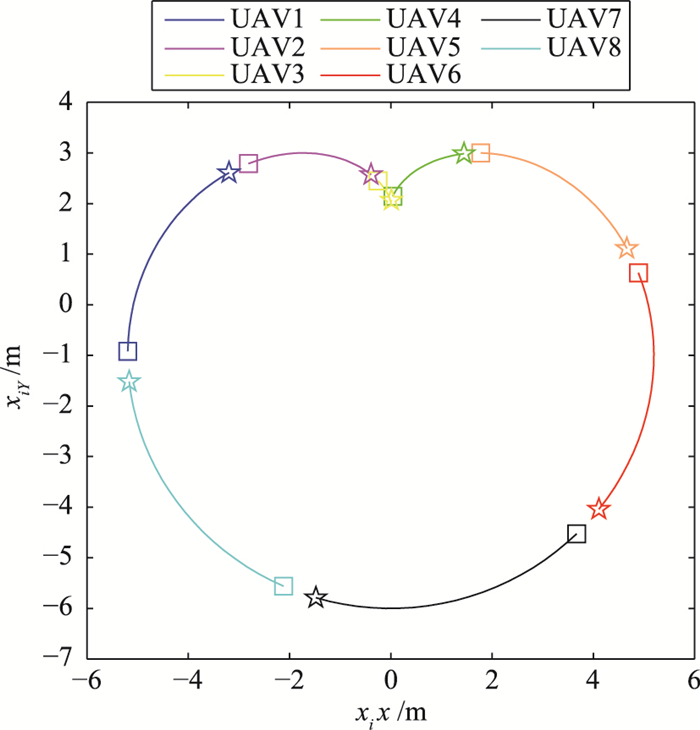
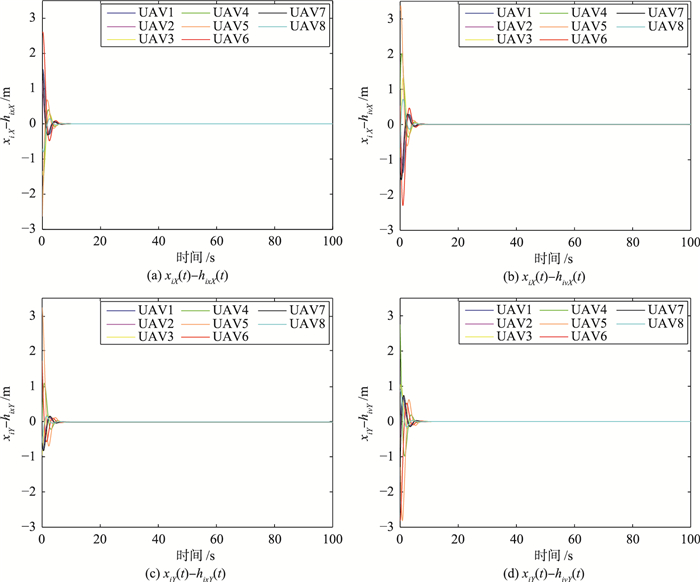
图 3给出了100 s内,每架无人机在二维水平面上的运动轨迹. 图 4为仿真时间在50 s~52 s之间,每架无人机的轨迹截图.其中,方框代表相应仿真时间的起点,五角星代表终点.从图 3和图 4可以看出,在时变时延和切换拓扑的通信约束下,8架无人机飞行一段时间后,形成了指定的编队,并且可以保持稳定. 图 5(a)~图 5(d)分别给出了每架无人机的4个状态与编队相应状态的差值曲线,可以看出,各无人机的状态与编队状态的差值随时间变化逐渐减小并逐渐趋于0.综上表明,无人机群系统在时变时延和切换通信拓扑的约束下形成了指定的编队.
|
| 图 3 无人机的运动轨迹 Figure 3 Motion trajectories of UAVs |
|
| 图 4 50 s~52 s轨迹截图 Figure 4 Snapshot of motion trajectories for t∈[50 s, 52 s] |
|
| 图 5 无人机状态与编队状态差值曲线 Figure 5 State curves of the difference between UAVs and formation |
文[28]将多主体支撑系统简化为一个二阶积分器模型,研究了固定拓扑条件下系统的协同控制问题,通过变量代换方法得到了LMI稳定判据.由注5可知,本文方法也同样适用于固定拓扑.为比较算法的保守性,在固定拓扑条件下,将本文方法得到的时延上界与文[28]方法进行比较. 表 1给出了3种不同拓扑情况下,两种方法分别得到的时延上界.
从表 1中可以看出,在三种拓扑条件下,利用本文方法得到的时延上界均大于文[28]方法.这说明本文的编队控制方法具有更小的保守性.本文在分析时延系统的镇定问题时,引入了自由权矩阵,得到了编队形成的LMI判据,并在求解过程中,对自由权矩阵的参数a和b进行了优化选取,因此得到了保守性更小的时延上界求解方法.
5 结论本文基于自由权矩阵方法,研究了线性群系统在具有时变时延和有向切换拓扑两个复杂通信条件下的编队控制问题.通过变量代换,将两个复杂通信条件下的群系统编队控制问题,转化为多个时延系统的镇定问题.利用自由权矩阵方法,对系统的镇定问题进行分析,得到了编队形成的LMI判据,以及时延上界和控制器增益的求解方法.与已有文献相比,本文考虑的通信条件更加复杂,得到的LMI判据保守性较小,且适用于大规模群系统.仿真实验证明了所提方法的有效性.
| [1] | Nigam N, Bieniawski S, Kroo I, et al. Control of multiple UAVs for persistent surveillance:Algorithm and flight test results[J]. IEEE Transactions Control Systems Technology, 2012, 20(5): 1236–1251. DOI:10.1109/TCST.2011.2167331 |
| [2] |
杨波, 方华京.
大规模群体系统的现状研究[J]. 武汉理工大学学报(信息与管理工程版), 2007, 29(1): 1–6.
Yang B, Fang H J. Study of large-scale swarm systems:State of art[J]. Journal of Wuhan University of Technology(Information & Management Engineering), 2007, 29(1): 1–6. |
| [3] | Feng X, Long W, Jie C, et al. Finite-time formation control for multi-agent systems[J]. Automatic, 2009, 45: 2605–2611. DOI:10.1016/j.automatica.2009.07.012 |
| [4] | Ren W. Consensus strategies for cooperative control of vehicle formation[J]. IET Control Theory and Application, 2007, 1(2): 505–512. DOI:10.1049/iet-cta:20050401 |
| [5] | Ren W, Sorensen N. Distributed coordination architecture for multi-robot formation control[J]. Robotics and Autonomous Systems, 2008, 56(4): 324–333. DOI:10.1016/j.robot.2007.08.005 |
| [6] | Seo J, Ahn C, Kim Y. Controller design for UAV formation flight using consensus based decentralized approach[C]//Proceedings of AIAA Infotech@Aerospace Conference. Reston, VA, US: AIAA, 2009: 1-11. |
| [7] | Dong X W, Yu B C, Shi Z Y, et al. Time-varying formation control for unmanned aerial vehicles:Theories and applications[J]. IEEE Transactions on Control Systems Technology, 2015, 23(1): 340–348. DOI:10.1109/TCST.2014.2314460 |
| [8] | Wang R, Dong X W, Li Q D, et al. Distributed adaptive control for time-varying formation of general linear multi-agent systems[J]. International Journal of Systems Science, 2017, 48(16): 3491–3503. DOI:10.1080/00207721.2017.1382602 |
| [9] |
焦建芳, 王光.
有向通信下的任务驱动船舶协同编队控制方法[J]. 信息与控制, 2017, 46(5): 606–613.
Jiao J F, Wang G. Task-driven cooperative formation control algorithm for vessels under directed communication topology[J]. Information and Control, 2017, 46(5): 606–613. |
| [10] | Liu C L, Tian Y P. Formation control of multi-agent systems with heterogeneous communication delays[J]. International Journal of Systems Science, 2009, 40(6): 627–636. DOI:10.1080/00207720902755762 |
| [11] | Rudy C G, Nejat O. Stability of formation control using a consensus protocol under directed communications with two time delays and delay scheduling[J]. International Journal of Systems Science, 2015, 47(2): 433–449. |
| [12] | Qin L G, He X, Zhou D H. Distributed proportion-integration-derivation formation control for second-order multi-agent systems with communication time delays[J]. Neurocomputing, 2017, 267: 271–282. DOI:10.1016/j.neucom.2017.05.088 |
| [13] | Abdelkader A, Abdelhamid T. Formation control of VTOL unmanned aerial vehicles with communication delays[J]. Automatica, 2011, 47(11): 2383–2394. DOI:10.1016/j.automatica.2011.08.042 |
| [14] | Dong X W, Xi J X, Lu G, et al. Formation control for high-order linear time-invariant multi-agent systems with time delays[J]. IEEE Transactions on Control of Network Systems, 2014, 1(3): 232–240. DOI:10.1109/TCNS.2014.2337972 |
| [15] |
石晓航, 张庆杰, 吕俊伟.
基于自由权矩阵的时变时延线性群系统编队控制[J]. 航空学报, 2017, 39(3): 204–214.
Shi X H, Zhang Q J, Lv J W. Formation control for linear swarm systems with time-varying delays based on free-weighting matrices[J]. Acta Aeronautica et Astronautica Sinica, 2017, 39(3): 204–214. |
| [16] | Dong X W, Zhou Y, Ren Z, et al. Time-varying formation control for unmanned aerial vehicles with switching interaction topologies[J]. Control Engineering Practice, 2016, 46: 26–36. DOI:10.1016/j.conengprac.2015.10.001 |
| [17] | Liu W, Zhou S L, Qi Y H, et al. Distributed formation control for multiple unmanned aerial vehicles with directed switching communication topologies[J]. Control Theory & Applications, 2015(10): 1422–1427. |
| [18] | Dong X W, Shi Z Y, Lu G, et al. Time-varying formation control for high-order linear swarm systems with switching interaction topologies[J]. IET Control Theory and Applications, 2014, 18(8): 2162–2170. |
| [19] | Wang R, Dong X W, Li Q D, et al. Distributed time-varying formation control for linear swarm systems with switching topologies using an adaptive output-feedback approach[J]. IEEE Transactions on Systems, Man, and Cybernetics:Systems, 2017. |
| [20] |
薛瑞彬, 宋建梅, 张民强.
具有时延及联合连通拓扑的多飞行器分布式协同编队飞行控制研究[J]. 兵工学报, 2015, 36(3): 492–502.
Xue R B, Song J M, Zhang M Q. Research on distributed multi-vehicle coordinated formation flight control with coupling time-delay and jointly-connected topologies[J]. Acta Armamentarii, 2015, 36(3): 492–502. |
| [21] |
张庆杰, 沈林成, 朱华勇.
具有多个通信时延的一类二阶多智能体系统平均一致性[J]. 控制与决策, 2011, 26(10): 1485–1492.
Zhang Q J, Shen L C, Zhu H Y. Average consensus of a class of second order multi-agent systems with multiple communication delays[J]. Control and Decision, 2011, 26(10): 1485–1492. |
| [22] | Zhang Q J, Niu Y F, Wang L, et al. Average consensus seeking of high-order continuous-time multi-agent systems with multiple time-varying communication delays[J]. International Journal of Control, Automation and Systems, 2011, 9(6): 1209–1218. DOI:10.1007/s12555-011-0623-3 |
| [23] | Ren W, Beard R W. Consensus seeking in multiagent Systems under dynamically changing interaction topologies[J]. IEEE Transactions on Automatic Control, 2005, 50(5): 655–661. DOI:10.1109/TAC.2005.846556 |
| [24] | Zhou S L, Liu W, Wu Q, et al. Leaderless consensus of linear multi-agent systems: Matrix decomposition approach[C]//Proceeding of the 7th International Conference on Intelligent Human-Machine Systems and Cybernetics. Piscataway, NJ, USA: IEEE, 2015: 327-331. |
| [25] | Boyd S, Ghaoui L E, Feron E, et al. Linear matrix inequalities in system and control theory[M]. Philadelphia, PA: SIAM, 1994. |
| [26] | Gu K. A further refinement of discretized Lyapunov functional method for the stability of time-delay systems[J]. International Journal of Control, 2001, 74(10): 967–976. DOI:10.1080/00207170110047190 |
| [27] | Bee O C E O. Matrix analysis[M]. New York, NJ, USA: Cambridge University Press, 1985. |
| [28] | Xi J X, Shi Z Y, Zhong Y S. Consensus analysis and design for high-order linear swarm systems with time-varying delays[J]. Physica A, 2011, 390(23/24): 4114–4123. |



