2. 江南大学轻工过程先进控制教育部重点实验室, 江苏 无锡 214122
2. Key Laboratory of Advanced Process Control for Light Industry(Ministry of Education), Jiangnan University, Wuxi 214122, China
0 引言
随着对生物群集行为及其一致性机制的不断研究,越来越多的科学家开始对其中潜在的相互作用或通信机制感兴趣.早在1959年,Woods[1]就提供了实验证据证明在蜜蜂群集形成过程中某种预测机制的存在.其他的研究者研究了生物群个体视觉和听觉组织上的预测功能,特别是在视网膜和皮质上进行的广泛的生物视觉实验发现,当个体观察者准备跟随一个视觉刺激的变化时,视觉适应是从当前位置转移到未来凝视的位置.这些研究支持了预测机制存在于许多生物体行为的猜想,比如蜥蜴捕食苍蝇,小狗叼飞盘,足球运动员争抢第一落点[2].这种预测机制减弱了系统集中传输时延的不利影响,促进了组目标或决策信息在组内个体间的传播,在许多生物群集的形成和演化中扮演着重要角色.受自然界生物具有“预测智能”的启发,将预测机制引入多自主体系统一致性的研究中是自然合理的选择.具有“预测智能”的每个自主体下一步行为的决策不仅取决于当前可利用的状态,也和未来状态的预测有关,这不仅更有利于一致性行为的产生,而且可以降低自主体相互通信的频率,节约系统能量,因此基于预测机制的多自主体系统的一致性研究受到控制理论学者越来越多的关注.
2008年,Zhang等[3]基于自然界生物“预测智能”的启发,融合预测控制里模型预测和滚动优化的思想,提出一种基于预测机制的一致性协议,即自主体不仅获取当前时刻自身及邻居的位置信息,同时也利用未来一段时间内自身及邻居的位置信息.仿真结果表明,该协议可以扩展系统采样周期和提高一致性收敛速度、同时对噪声有很好的鲁棒性. Ferrari-Trecate等[4]完全从预测控制的角度出发,针对带输入约束的1阶、2阶多自主体系统,利用最优路径的几何性质,在一些假设条件下证明多自主体能够渐近达到一致,但是没有得出解析解,在一定程度上不能满足实际应用中的实时性要求.席裕庚等[5]针对1阶连续多自主体系统,在Olfati-Saber等[6]提出的基本一致性协议的基础上引入状态预测器预测状态的变化趋势,即自主体在当前时刻可获取自身及邻居的速度信息,以增加一次通信的代价增大了多自主体系统的最小非零特征值,从而提高了一致性收敛速度. Zhan等[7]针对1阶离散多自主体系统,分别在固定和切换拓扑下设计了分布式MPC加权平均一致性协议,此协议中假定每个自主体及其邻居构成一个子系统,每个子系统的MPC最优解的加权平均值作为原系统的控制解,在提高系统收敛速度的同时可以平缓控制量变化,减少稳态误差. Cheng等[8]针对1阶离散系统自主体系统,在切换拓扑结构下设计了基于MPC的一致性协议,利用随机矩阵理论给出了采样周期范围和一致性收敛的充分条件,并证明:与增加闭环系统自由度相比,基于预测机制的一致性协议能扩展控制时域. Wu等[9]针对2阶连续自主体系统,在文[10]所提协议基础上增加状态预测项,利用特征值分析给出了预测项参数的范围,仿真表明通过选取合适的预测项参数可以提高自主体的收敛速度. Zhou等[11]针对2阶离散自主体系统,提出分布式模型预测控制(DMPC)策略并给出其反向迭代解,利用李亚普诺夫稳定性定理证明系统在其控制解下的稳定性. Gao等[12]考察了2阶连续非线性多自主体系统,提出了分布式MPC算法,为每个自主体分别设计正不变终端域和辅助控制器,给出时变兼容性约束以保证系统的稳定性.季虹菲等[13]在文[14]提出的一致性协议的基础上,把预测项改进为具有拓扑结构约束的形式,通过预测和优化得到反馈系数,但是其解不具有显式解析形式,故用大量数值仿真分析预测参数对系统性能的影响. Liu[15]考虑了基于网络连接的多自主系统,设计传输策略处理数据丢包,用预测方法来补偿因网络通信产生的延时,得到了一致性和稳定性相结合的充要条件.
以上工作都将预测机制引入到多自主体一致性协调控制问题上,通过付出给予自主体存储过去状态和预测能力而产生的代价,自主体可以有效减少通信能量和成本,提高一致性性能(收敛速度、收敛步长、采样周期范围等),同时预测控制(如MPC)有着高度的机动性和灵活性,可以通过调节相应参数更好地满足多自主体系统的控制需求.
在1阶多自主系统的一致性问题研究中,自主体的位置是唯一需要通过控制作用达到一致的量,一致性协议常常是通过自主体邻居间位置信息来间接获得自主体的速度,从而实现对自主体位置的控制.在现实物理世界中,物体的速度变化是通过加速度即力的作用来实现的,而多自主体的速度又影响着其位置的变化,因此2阶多自主体系统的一致性问题更加具有实际意义[9-11, 16-18]. 2阶多自主体系统中的位置和速度都是需要到达一致的量,一致性协议常常是通过控制自主体的加速度来实现对自主体速度和位置的控制,根据速度是否收敛到0,可以分为静态一致性协议[9-10, 16, 19]和动态一致性协议[17-18].与1阶多自主体系统相比,2阶多自主体系统的一致性不仅依赖于系统的拓扑结构,同时一致性协议参数更多,而且其计算量和收敛性分析更加复杂.
本文研究对象是2阶离散多自主体系统,假设自主体具有某些“生物智能”,设计了基于预测项的2阶一致性协议,通过梯度下降法求解性能指标函数给出基于MPC的最优控制解,继而根据代数理论得到其等价控制解,给出了多自主体系统达到一致性的充分必要条件,并分析了协议参数对系统收敛性的影响,最后数值仿真验证了理论的正确性.
1 问题描述 1.1 图论及符号对于由N个自主体组成的多自主体系统,用G=(V,E,A)来描述其信息交互结构,其中节点集V={v1, v2, …, vN}对应N个自主体,边集E⊆{(vi, vj):vi, vj∈V, vi≠vj}对应自主体之间的信息传递,边的权重表示为: aij≥0,aii=0,其对应的邻接矩阵为A=[aij]N×N.每个节点vi的输出度定义为: 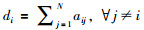
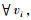
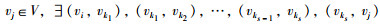
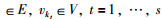
在本文中,Rm、Rmn、Rm×n分别表示m维、mn维和m×n维向量(矩阵). 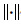
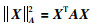
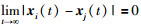
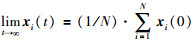
2阶多自主体动态模型描述为
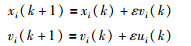
|
(1) |
其中,xi∈R代表每个自主体的位置,vi∈R代表每个自主体的速度,ui∈R代表每个自主体的输入,ε>0是采样周期.研究目标是设计合理的一致性协议ui(k),使所有自主体的位置、速度都达到渐近一致,即:
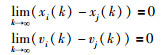
|
目前,有关系统(1)的一致性协议大都以Ren等[19]提出的基于状态反馈的协议为基础,其离散形式的一般表达式为
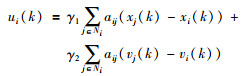
|
(2) |
其中,aij>0是自主体间的连接权重,γ1, γ2>0是控制增益. Ren提出的协议是式(2)的特例,即γ1=0.
若系统(1)包含一棵有向生成树,则通过调节γ1、γ2使之满足一定条件时,协议(2)可以使系统达到动态一致.但是协议(2)仅依靠内部作用调整自主体状态,信息交流完全依赖系统拓扑,系统的收敛速度完全取决于参数的调节,没有充分挖掘其它有用信息,如自主体的历史信息、二层邻居信息、网络拓扑的连接属性等.尽管系统的收敛速度和γ1、γ2有关,但是当γ1、γ2确定下来时收敛速度也就确定了.如果自主体的速度收敛到0,即系统中的自主体最终都达到同一位置,就认为协议(2)实现了静态一致性.可以看出,静态一致性是动态一致性的特例,Ren等[20]提出一个静态一致性协议,其相应的离散形式为
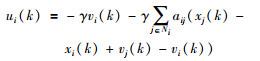
|
(3) |
假设所有自主体具有某种程度的“预测智能”,提出一致性协议:
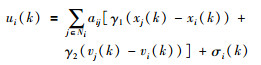
|
(4) |
其中,σi(k)∈R为预测项,通过求解性能指标得到.
令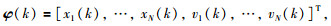
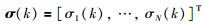
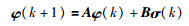
|
(5) |
其中,
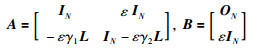
|
由式(5)可以预测未来Hp步内的自主体信息:
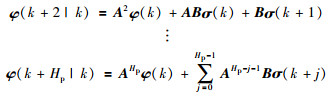
|
(6) |
其中Hp是预测时域,式(6)可以简化为
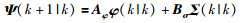
|
(7) |
其中,
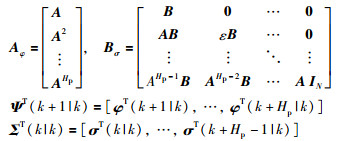
|
为了实现多自主体一致性的控制目标,定义式(8)的参考轨迹,即对自主体本身和其邻居当前时刻的位置和速度求平均值:
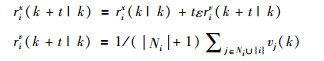
|
(8) |
其中,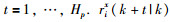
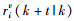
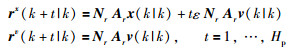
|
其中,
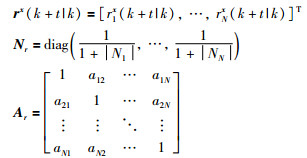
|
令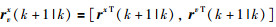
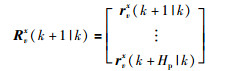
|
因此参考轨迹可以简化为
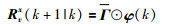
|
(9) |
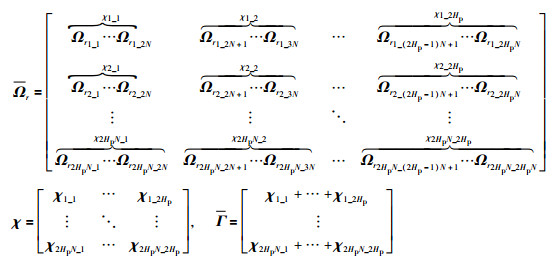
其中,φ(k|k)=φ(k),hi_j表示矩阵H中的第i行第j列元素.
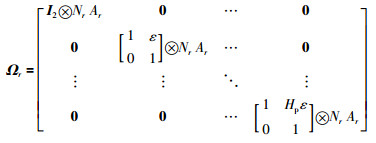
|
|
建立二次型性能指标:
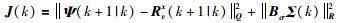
|
(10) |
为了区分状态和速度对性能指标的影响,定义控制权矩阵:
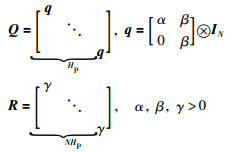
|
式(10)中的第1项是对自主体状态偏离期望值的惩罚,第2项是对绝对控制量的惩罚.
由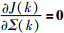
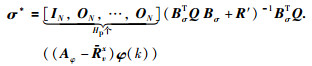
|
(11) |
其中,
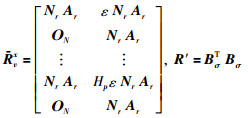
|
式(11)是直接用MPC方法得到的,在MPC中,求解性能函数常常使用下降梯度、内点法、可行域内枚举、地毯式搜索等方法,在自主体数量较小时比较方便、快速,但实际自主体系统的规模都很大(比如由几十个甚至几百个自主体构成),用上述方法求解性能函数时会给计算机造成计算和存储压力,影响在线计算的速度,不能满足实时性的要求.式(11)虽然可以一次性离线计算出,但是含有逆矩阵,不仅会产生计算量大的问题,而且给分布式多自主体系统的稳定性分析带来一定挑战.在下一节中将利用相应的代数理论,给出性能函数(10)另一种形式的解析解,也是式(11)的控制等价解,它是准确解而不是渐近最优解.
2.2 MPC最优解的等价形式定理1 关于向量x∈Rn,v∈Rn的二次多项式为
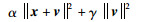
|
其中,α, γ>0,存在a=α+γ,c=α/(α+γ),d=αγ/(α+γ),使得上面的二次多项式可以改写为
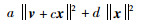
|
证明 代入即可.
如果α=β,式(10)可以写成:
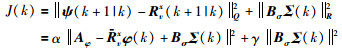
|
根据定理1,式(10)可以写成:
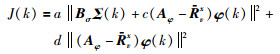
|
(12) |
当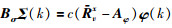
根据滚动优化原理,取第1项为实际控制作用,此时: 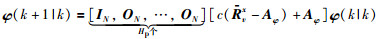
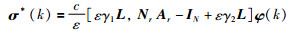
|
(13) |
可以看出,等价解(13)是简单的线性反馈形式,参数和自主体系统的拓扑结构和采样周期有关.和式(11)相比,不含有逆矩阵,计算需求量小(特别在N很大情况下),参数选取较方便,有利于系统的稳定性分析.
系统(1)在等价解(13)作用下可以表述为
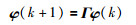
|
(14) |
其中,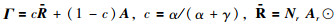
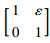
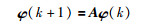
|
(15) |
当ε=1,多自主体系统(1)在协议(2)下渐近达到一致,当且仅当系统拓扑图含有有向生成树且参数γ1和γ2满足文[18]中定理3-2:
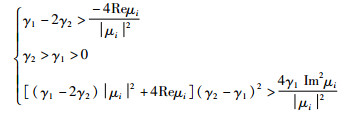
|
其中,μi是拉普拉斯矩阵L的非零特征值.
3 一致性证明引理1[21] 如果无向图G是连通的,其对应的拉普拉斯矩阵L是对称的且是半正定的,有且只有一个零特征值且其余特征值都是正实数.
引理2[21] 如果有向图G包含向生成树,其对应的拉普拉斯矩阵L有且只有一个零特征值且其余特征值都具有正实部.
引理3 如果方阵A和单位阵I是同阶的,则有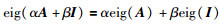
证明 特征值定义代入即可.
定理2 如果多自主体系统(1)的拓扑结构是无向连通的或者是有向连通且包含有向生成树,那么Γ有且仅有两个不依赖于c的1特征值.
证明 如果无向图G连通或有向图G包含有向生成树,由引理1或引理2可知,图G对应的拉普拉斯矩阵L的0特征值的代数重数为1.假设λ是A的一个特征值, μi是L的特征值,根据引理3,有:
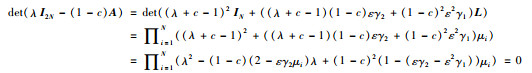
|
于是:
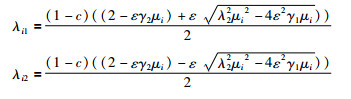
|
由上式可知,若μi=0时,λi1=λi2=1-c,则(1-c)A的1-c特征值的代数重数为2.同理可得cR的c特征值的代数重数也为2,所以Γ必然有两个不依赖于c的1特征值.
定理3 如果Γ的1特征值的代数重数为2且其余特征值都在单位圆内,则多自主体系统(1)能达到动态一致:
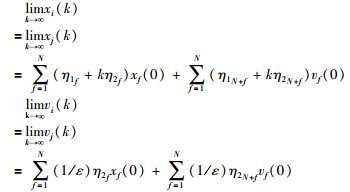
|
其中,
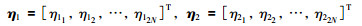
|
分别是Γ关于1特征值的广义左特征向量和左特征向量.
证明 先证明充分性.注意到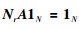
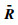
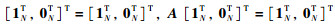
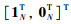
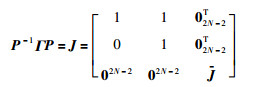
|
其中,P2N×2N是非奇异矩阵,J由Γ的非1特征值组成的约当块矩阵.于是可得:
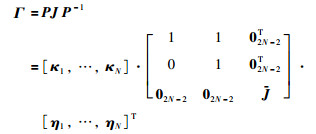
|
(16) |
其中,κi和ηi(i=1, 2, …, N)分别是Γ的右特征向量(广义右特征向量)和左特征向量(广义左特征向量).
因为Γ的1特征值的几何重数为1,所以κ1=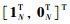
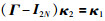
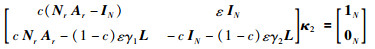
|
可得Γ关于1特征值的另一广义右特征向量κ2=(1/ε).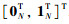
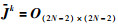
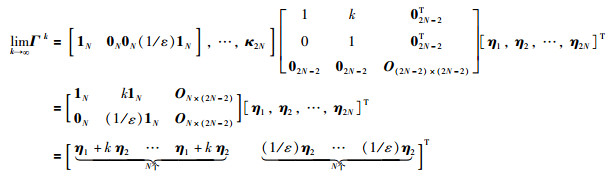
|
(17) |
由式(14)有: 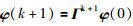
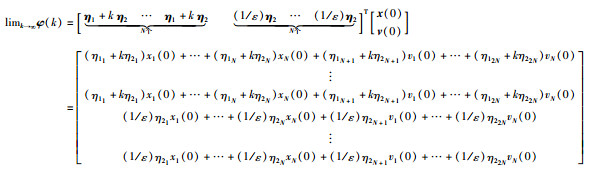
|
(18) |
其中,η1和η2如定理3中所述.由此可见,多自主体系统到达渐近动态一致,自主体状态和速度满足定理3中的等式.
必要性采用反证法证明.
如果定理3中的条件“Γ的1特征值的代数重数为2且其余特征值都在单位圆内”不成立的话,由定理2可知,Γ至少有两个1特征值.因此有3种情况:
1) Γ有且仅有两个1特征值且至少有一个特征值不在单位圆内;
2) Γ有大于两个的1特征值且其它所有特征值都在单位圆内;
3) Γ有大于两个的1特征值且至少有一个特征值不在单位圆内.
对于情况1)和情况3),由线性离散系统稳定性定理可知系统是不稳定的,因此系统不能达到渐近一致; 对于情况2),Γ依赖于c的1特征值对应的特征向量κi和ηi(i=3, 4,…)不能使式(17)成立,即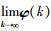
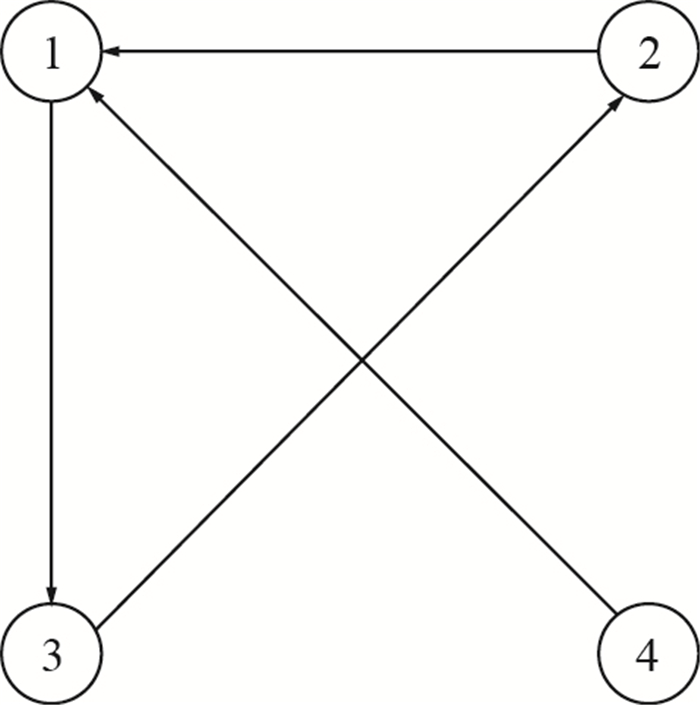
为了验证本文定理的有效性和预测机制的引入对多自主体一致性性能的改善,分别将协议(2)和协议(4)作用于具有动态特性式(1)的4自主体系统,其通信拓扑结构是有向固定的,含有有向生成树,有向边的权重为1,不存在自连接(如图 1).自主体的初始位置和速度分别为x(0)=[-10 20 30 -40]T, v(0)=[3 -4 5 -6]T.
|
| 图 1 4自主体拓扑图 Figure 1 Four agents′ communication topology |
可以看出图 1所示拓扑图含有有向生成树,其拉普拉斯矩阵为

|
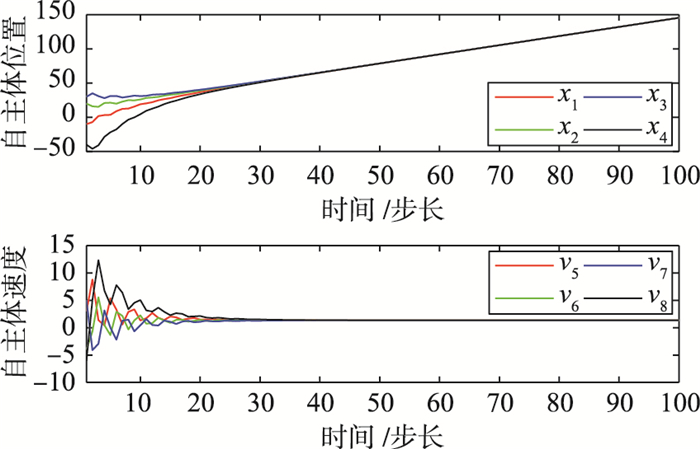
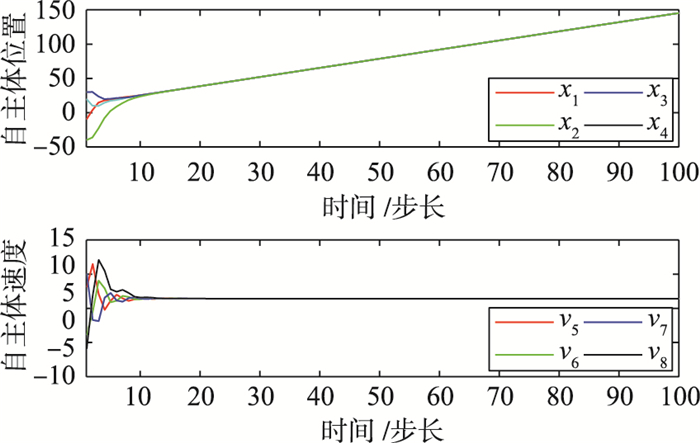
其特征值分别为: λ1=0, λ2=1, λ3=1.5+0.866i,λ4=1.5-0.866i,对于协议(2),取参数γ1=0.1, ε=1,γ1=0.1, γ2=0.9,满足文[18]中定理3-2,矩阵A的特征值为: -0.231 5±0.7846i, 0.2298, 0.8702, 0.8815±0.0052i, 1(二重),自主体的位置和速度信息演化过程如图 2所示,经过约50步所有自主体的位置和速度渐近趋于一致; 对于协议(4),取参数ε=1, γ1=0.1, γ1=0.9, α=1, γ=1,矩阵Γ的特征值0.021 1±0.637 9i, 0.410 44, 0.553 9±0.184 9i, 0.639 6(二重),满足定理3中的条件,自主体的位置和速度信息演化过程如图 3所示,经过约25步所有自主体的位置和速度渐近趋于一致.可见,在参数条件相同下,引入预测机制的协议提高了自主体的收敛速度.
|
| 图 2 ε=1, γ1=0.1, γ2=0.9时自主体的位置和速度(协议(2)) Figure 2 Agents′ positions and velocities (protocol (2)) when ε=1, γ1=0.1, γ2=0.9 |
|
| 图 3 ε=1, γ1=0.1, γ2=0.9时自主体的位置和速度(协议(4)) Figure 3 Agents′ positions and velocities (protocol (4)) when ε=1, γ1=0.1, γ2=0.9 |
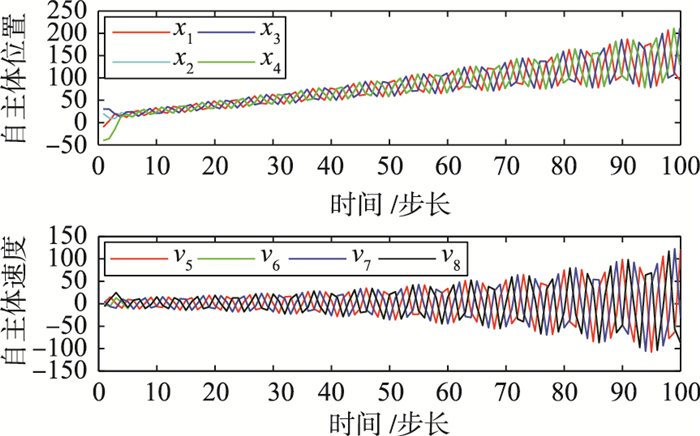
当协议(4)中的参数为ε=1, γ1=0.5, γ2=1.5,α=1, γ=1时, 矩阵Γ的特征值为:0.415 2±0.1i, 0.375±0.216 5i, -0.290 2±0.982 5i, 1(二重),有两个特征值在单位圆外,不满足定理3中的条件,自主体的位置和速度信息演化过程如图 4所示,显然,自主体的位置和速度不能渐近趋于一致.
|
| 图 4 ε=1, γ1=0.5, γ2=1.5时自主体的位置和速度(协议(4)) Figure 4 Agents′ positions and velocities (protocol (4)) when ε=1, γ1=0.5, γ2=1.5 |
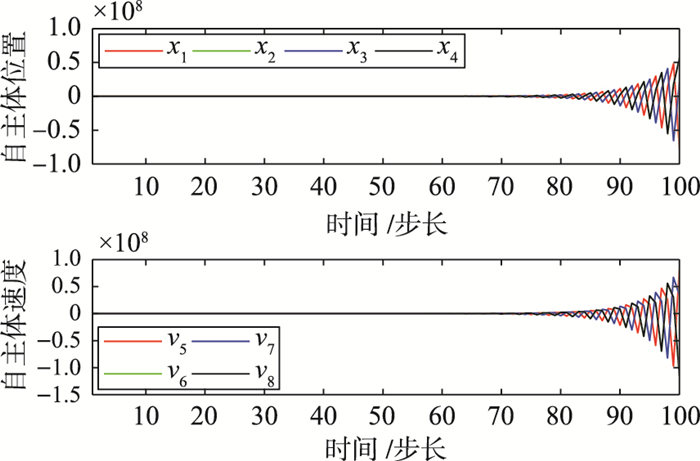
当协议(2)中的参数为ε=1.3, γ1=0.1, γ2=0.9时,自主体的位置和速度不能渐近趋于一致(如图 5所示); 当协议(4)中的参数为ε=2.5, γ1=0.1, γ2=0.9,α=0.8, γ=0.2时,自主体的位置和速度仍可以渐近趋于一致(如图 6).可见,在参数条件相同的情况下,引入预测机制的协议扩展了自主体系统的采样周期.
|
| 图 5 ε=1.3, γ1=0.1, γ2=0.9时自主体的位置和速度(协议(2)) Figure 5 Agents′ positions and velocities (protocol (2)) when ε=1.3, γ1=0.1, γ2=0.9 |
|
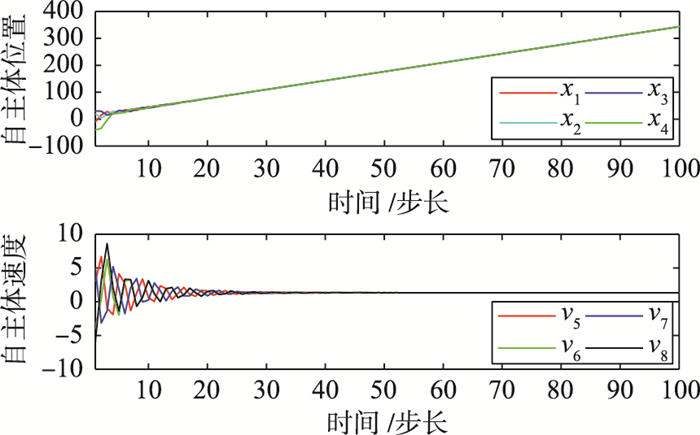
| 图 6 ε=2.5, γ1=0.1, γ2=0.9时自主体的位置和速度(协议(4)) Figure 6 Agents′ positions and velocities (protocol (4)) when ε=2.5, γ1=0.1, γ2=0.9 |
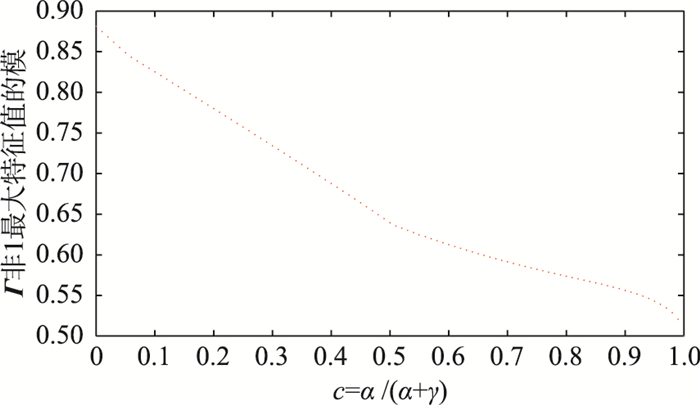
由式(14)可知,多自主体系统(1)在协议(4)的MPC等价解(式(13))的作用下的收敛速度和Γ的特征值模的大小有关,如果Γ满足定理3,Γ的非1特征值越接近原点,系统达到一致的速度就越快,引入预测机制能提高系统收敛速度的根本原因在于把Γ的非1特征值拉向原点.把权参数0 < c=α/(α+γ) < 1等间距取100个值,其余参数为ε=1, γ1=0.1, γ2=0.9,仿真100次,可以发现: Γ的非1最大特征值模是权参数0 < c < 1的减函数(图 8).特别地,当c=0时,式(14)退化成式(15),即没有引入预测机制,Γ的非1最大特征值模取得最大值,所以在相同增益γ1、γ2下,引入预测机制总能提高自主体系统的收敛速度.
|
| 图 8 Γ特征值和权参数的关系 Figure 8 Relationship between Γ′s eigenvalues and weight parameters |
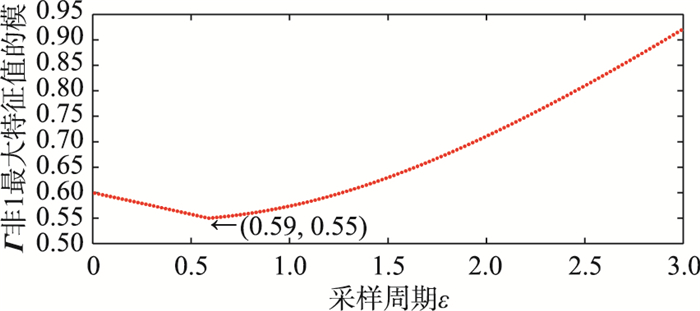
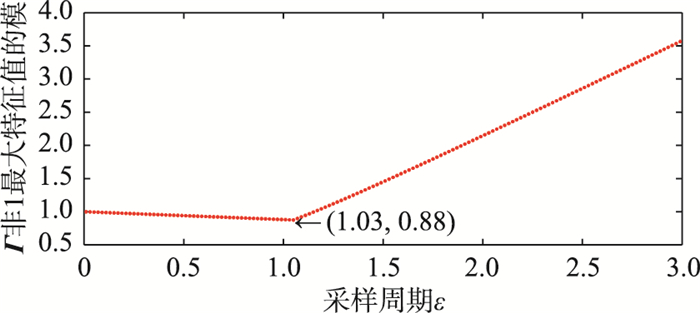
同样地,把采用周期ε在[0.01 3.01]等间距取100个值,其余参数为c=0.8, γ1=0.1, γ2=0.9,仿真100次,可以发现: Γ的非1最大特征值模随着采用周期ε的增大先减小后增大,总存在使Γ的非1最大特征值模取得最小值的采样周期ε(图 9,ε=0.59,Γ的非1最大特征值为0.55).特别地,当c=0时,式(14)退化成式(15),即没有引入预测机制,Γ的非1最大特征值模也随着采用周期ε的增大先减小后增大,也总存在使Γ的非1最大特征值模取得最小值的采样周期ε(图 10,ε=1.03,Γ的非1最大特征值为0.88).但是,在相同增益γ1、γ2和采样周期ε下,引入预测机制的情形下Γ的非1最大特征值更接近原点,使得可允许的采样周期范围更大,因此引入预测机制总可以扩展多自主体系统的采样周期.
|
| 图 9 Γ特征值和采样周期的关系(协议(4)) Figure 9 Relationship between Γ′s eigenvalues and sampling intervals (protocol (4)) |
|
| 图 10 Γ特征值和采样周期的关系(协议(2)) Figure 10 Relationship between Γ′s eigenvalues and sampling intervals (protocol 2) |
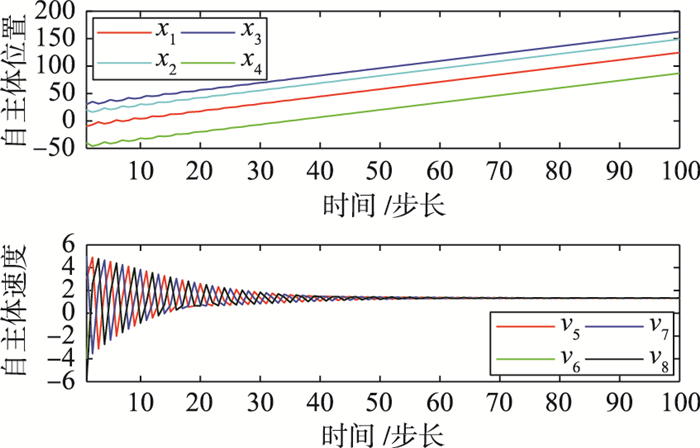
通过仿真可以发现: 1)调节权矩阵Q和R中的参数α、β、γ,可以提高自主体状态的收敛速度,即c(受α、β、γ影响)越大,收敛速度越快; 在相同的控制增益γ1、γ2下,引入预测机制的协议(4)总是比未引入预测机制的协议(2)更有利于自主体的一致性行为. 2)调节权矩阵Q和R中的参数α、β、γ,可以扩展自主体系统的采样周期,ε和c没有具体的解析关系; 在相同的控制增益γ1、γ2下,引入预测机制的协议(4)总是比未引入预测机制的协议(2)更有利于节约自主体系统的通信能量. 3)基于预测机制的等价解(12)中参数若满足定理3中的条件,总能使多自主体状态收敛到动态一致(不为0),而最优解(11)可能不能使自主体位置收敛的一致(图 7),因为用数值方法得到的最优解(11)是一个渐近解,而不是准确解.
|
| 图 7 ε=1, γ1=0.1, γ2=0.9, Hp=3时自主体的位置和速度(最优解11) Figure 7 Agents′ positions and velocities (optimal solution (11)) when ε=1, γ1=0.1, γ2=0.9, Hp=3 |
多自主体状态的收敛速度是多自主体系统一致性研究中重点讨论对象,如何提高收敛速度是值得研究的问题.不同于1阶积分器多自主体系统,2阶积分器多自主体系统的一致性实现不仅依赖于系统的通信拓扑结构,还与协议中的参数密切相关.设计合理高效的2阶一致性协议(调节较少的参数,快速达到一致性目标)是本文主要探讨的问题.通过赋予自主体“预测智能”,假设自主体可以预测未来有限时间内的局部状态,利用更多自主体可以感知的信息,设计了基于预测项的2阶动态一致性协议,得到基于MPC的最优解和等价解. 2阶多自主体系统在该协议等价解的作用下,可以提高收敛速度和扩展采样周期,能避免最优解含逆矩阵、非准确解、参数调节不易等问题,同时给出系统达到动态一致的充分必要条件.一个仿真实例说明了理论的有效性,对于本文的研究内容还可以作更深刻的探讨.
| [1] | Woods E F. Electronic prediction of swarming in bees[J]. Nature, 1959, 184: 842–844. DOI:10.1038/184842a0 |
| [2] |
詹璟原. 多智能体系统预测协同控制研究[D]. 上海: 复旦大学, 2013. Zhan J Y. Study on predictive and cooperative control for multi-agent system[D]. Shanghai: Fudan University, 2013. |
| [3] | Zhang H T, Chen M Z Q, Stan G B. Collective behavior coordination with predictive mechanisms[J]. IEEE Circuits & Systems Magazine, 2008, 8(3): 67–85. |
| [4] | Ferrari-Trecate G, Galbusera L, Marciandi M P E. Model predictive control schemes for consensus in multi-agent systems with single-and double-integrator dynamics[J]. IEEE Transactions on Automatic Control, 2009, 54(11): 2560–2572. DOI:10.1109/TAC.2009.2031208 |
| [5] |
席裕庚, 黄维, 李晓丽.
具有状态预测器的多智能体系统一致性研究[J]. 控制与决策, 2010, 25(5): 769–772.
Xi Y G, Huang W, Li X L. Consensus of multi-agent system with state predictor[J]. Control and Decision, 2010, 25(5): 769–772. |
| [6] | Olfati-Saber R, Fax J A, Murray R M. Consensus and cooperation in networked multi-agent systems[J]. Proceedings of the IEEE, 2007, 95(1): 215–233. DOI:10.1109/JPROC.2006.887293 |
| [7] | Zhan J Y, Li X. Consensus of sampled-data multi-agent networking systems via model predictive control[J]. Automatic, 2013, 49(8): 2502–2507. DOI:10.1016/j.automatica.2013.04.037 |
| [8] | Cheng Z M, Fan M C, Zhang H T. Distributed MPC based consensus for single-integrator multi-agent systems[J]. ISA Transactions, 2015, 58: 112–120. DOI:10.1016/j.isatra.2015.03.011 |
| [9] | Wu J, Zhang L Y, Bai Y. Fast second-order consensus via predictive mechanisms[J]. Epl, 2015, 109(1): 10–19. |
| [10] | Qin J, Gao H, Zheng W X. Second-order consensus for multi-agent systems with switching topology and communication delay[J]. Systems & Control Letters, 2011, 60(6): 390–397. |
| [11] | Zhou L, Li S Y. Distributed model predictive control for consensus of sampled-data multi-agent systems with double-integrator dynamics[J]. IET Control Theory & Applications, 2015, 9(12): 1774–1780. |
| [12] | Gao Y, Dai L, Xia Y. Distributed model predictive control for consensus of nonlinear second-order multi-agent systems[J]. International Journal of Robust & Nonlinear Control, 2017, 27(5): 830–842. |
| [13] |
季虹菲, 席裕庚, 李晓丽.
多智能体一致性预测控协议及其仿真研究[J]. 计算机仿真, 2010, 27(12): 186–190.
Ji H F, Xi Y G, Li X L. Simulation study on multi-agent system under MPC[J]. Computer Simulation, 2010, 27(12): 186–190. DOI:10.3969/j.issn.1006-9348.2010.12.046 |
| [14] | Zhang H T, Chen M Z Q, Zhou T. Ultrafast consensus via predictive mechanisms[J]. Epl, 2009, 83(4): 4003p1–4003p6. |
| [15] | Liu G P. Consensus and stability analysis of networked multiagent predictive control systems[J]. IEEE Transactions on Cybernetics, 2017, 47(4): 1114–1119. DOI:10.1109/TCYB.2016.2535126 |
| [16] | Xie D, Liang T. Second-order group consensus for multi-agent systems with time delays[J]. Neurocomputing, 2015, 153: 133–139. DOI:10.1016/j.neucom.2014.11.044 |
| [17] |
黄红伟, 黄天民, 吴胜.
基于事件触发的二阶多智能体系统平均一致性[J]. 信息与控制, 2016, 45(6): 729–734.
Huang H W, Huang T M, Wu S. Event-triggerd average consensus of second-order multi-agent systems[J]. Information and Control, 2016, 45(6): 729–734. |
| [18] | Xie D, Wang S. Consensus of second-order discrete-time multi-agent systems with fixed topology[J]. Journal of Mathematical Analysis & Applications, 2012, 387(1): 8–16. |
| [19] | Ren W, Beard R W. Consensus seeking in multiagent systems under dynamically changing interaction topologies[J]. IEEE Transactions on Automatic Control, 2005, 50(5): 655–661. DOI:10.1109/TAC.2005.846556 |
| [20] | Ren W, Atkins E. Distributed multi-vehicle coordinated control via local information exchange[J]. International Journal of Robust & Nonlinear Control, 2007, 17(10/11): 1002–1033. |



