0 引言
相较于传统的控制系统,网络化控制系统(networked control systems,NCS)以数字网络作为反馈通道,能够有效降低系统维护成本、增强系统可扩展性、便于实现远距离控制.近些年已有许多关于NCS的研究成果[1-2].但是由于数字网络的加入,当NCS中的传感器需要将一个测量到的物理量发送到控制器时,需先将物理量进行量化编码,再通过网络信道传输.量化过程不可避免地会带来量化误差、导致反馈信号精度损失,从而会损害控制性能、甚至破坏系统稳定性.量化器根据量化的方式分为均匀量化器、对数量化器等,根据量化区间是否动态变化分为动态量化器和静态量化器.文[3-4]研究了采用静态对数量化器系统的稳定条件.文[5-7]研究了动态量化策略,指出系统的渐近稳定性能够在有限反馈比特率下实现,其中文[5]给出了保证系统稳定性的充分必要比特率条件.
尽管单个NCS占用的网络资源可能不多,但随着NCS应用数量的快速增长网络资源的占用压力越来越大,如何提高网络资源的利用效率成为亟需解决的问题.事件触发采样策略是近些年涌现出的一种有效节省网络资源的方法.与传统周期性采样策略相比,事件触发仅在某一预设条件满足后触发采样,能够减少采样的次数[8-10].文[8-9]研究了针对L2稳定性和ISS(input-to-state stability)的事件触发条件设计方法.文[10]将事件触发与周期采样进行对比,展示了在控制性能相同的情况下,事件触发的平均采样周期更长.文[11-12]在经典事件触发的基础上研究了自触发采样控制.文[13]将事件触发应用到了分布式系统中,用于减少大型NCS中信息拥塞问题,并考虑了丢包和信道时延.
许多事件触发研究是建立在反馈信号能够精确传输条件下的,该条件要求反馈网络带宽为无穷大,但实际网络带宽通常是有限的.文[14]指出文[5]中的反馈比特率在事件触发下仍能确保系统稳定性.文[15-16]以状态误差作为触发条件,因此当事件触发时,只需量化误差区间的表面;这种量化方式充分利用了事件触发控制的性质,在节省量化比特数的同时提高了量化精度.
为了延长系统的触发间隔、减少对反馈网络资源的占用,可以采用基于模型的控制方法,在控制器中引入系统模型,对系统实时状态进行估计并计算控制量[17].但在实际应用中,不易得到精确系统参数,模型参数与系统参数之间有误差,即存在模型不确定性.文[18-19]研究了模型不确定性给系统带来的影响,并给出使系统稳定的模型误差限定条件.文[20]研究了考虑模型不确定性的事件触发控制系统,给出了模型误差限定条件和事件触发条件,同时还研究了引入静态对数量化器后控制策略的设计方法.但这种静态量化方法只有在量化比特数无限多时系统才能渐近稳定,因此不能应用在实际系统中.
在以上文献的基础上,本文研究具有模型不确定性的事件触发系统,采用动态均匀量化器,在有限比特率下保证了系统的渐近稳定性.相较于文[20],本文在实际工程中更易实现.
1 系统描述本节首先介绍一些基本定义、符号和系统模型,并对所研究问题进行了数学上的描述.
定义 Rn为n维欧几里得空间;状态量x是一个在时间上的映射,定义为x:R→R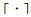
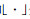
在本文研究的事件触发系统中,假设不存在计算时延和网络传输时延,并且网络无丢包,因此系统触发采样后,控制器可以立即收到量化后的采样信息,并用于更新模型状态和控制量.定义sk(k∈Z0+)为第k次事件触发时刻,定义sk-和sk+分别表示触发时刻的前一瞬间和后一瞬间.
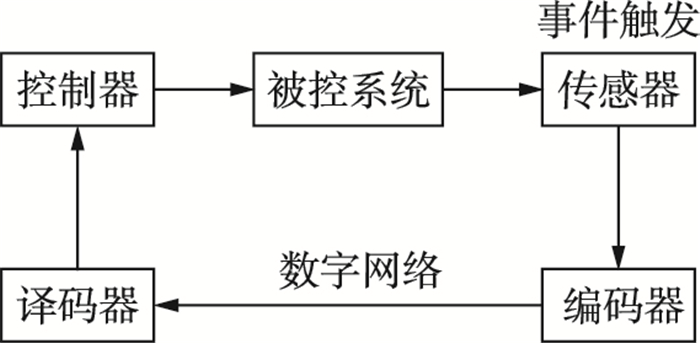
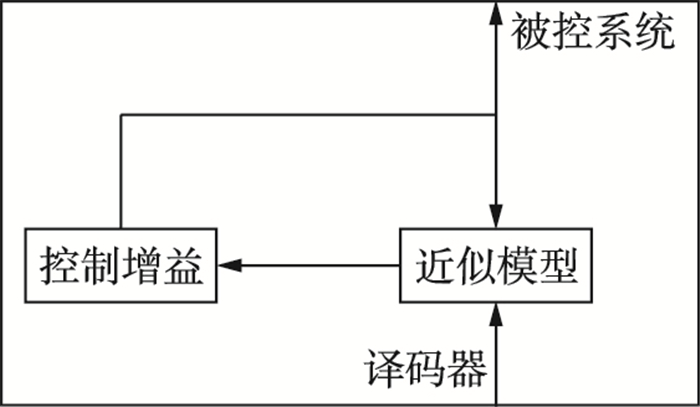
1.1 基于模型的事件触发控制系统本文所研究的系统结构如图 1所示.在该系统中,采样后控制器才能得到关于系统状态的信号.为了尽量延长两次触发之间的间隔,在控制器中运行一个近似模型用于估计系统的实时状态.由于系统精确参数不易得到,因此本文中基于模型的网络化控制系统考虑了模型与实际系统之间的模型不确定性.因为事件触发需要实时监测模型状态和系统状态之差,故传感器中也包含了一个与控制器中相同的近似模型且每次触发采样更新时也采用量化后的信息更新,以保证传感器与控制器中的模型状态相同.因此,后面不再区分这两个模型状态,都用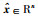
|
| 图 1 系统结构 Figure 1 The system structure |
|
| 图 2 基于模型的控制器节点 Figure 2 The model-based controller node |
系统与模型的状态方程为
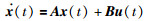
|
(1) |
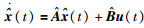
|
(2) |
其中,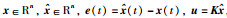
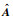
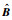
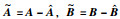
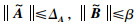
|
类似文[20],可得如下引理:
引理1 对于n维系统(1)和模型(2),控制量为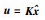
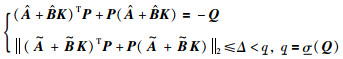
|
(3) |
其中,Δ为模型误差的上界.若采用式(4)的触发条件,则系统渐近稳定:
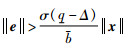
|
(4) |
其中,0 < σ(·) < 1,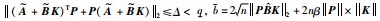
证明 定义李亚普诺夫函数为V=xTPx,求导可得
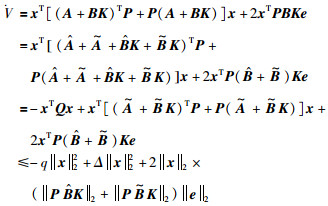
|
(5) |
可知:
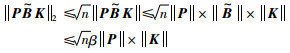
|
式中应用了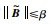
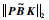
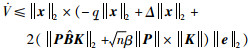
|
(6) |
当采用式(4)作为系统的触发条件时,总满足:
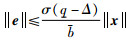
|
(7) |
根据式(7)可得‖e‖2的上界:
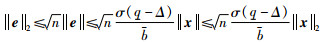
|
(8) |
将式(8)代入式(6),可得:
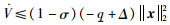
|
(9) |
因此系统渐近稳定.
这个引理提供了在模型不确定性情况下,保证系统渐近稳定性的事件触发条件及模型误差限定条件.
1.2 表面量化的均匀量化器相对于传统的周期采样系统,事件触发控制系统每当模型误差满足预设条件时才进行采样,并且在连续两次触发之间,系统和模型状态是连续变化的.假设系统的触发条件形式为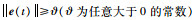
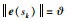
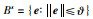
对式(1)中的n维系统,用xi表示状态向量x∈Rn中的第i项(i=1,2,…,n).定义碰撞维I表示满足|ei|=ϑ的最小系数i.量化器在每一维上的量化区间个数为l,l∈Z+,l>1.定义符号集合S={′p′,′n′,0,1,…,l-1},其中′p′,′n′分别表示正和负;量化器Q:Rn→Sn.量化时,首先从n维向量中找出碰撞维,状态误差在碰撞维上的可能取值为±ϑ,则有当i=I时:
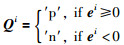
|
(10) |
可以用1比特表示.量化其余的n-1维时,量化器分别将各维均匀地划分成l个等长子区间并编号,将状态误差用其所在的子区间编号表示,即当i≠I时:
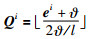
|
(11) |
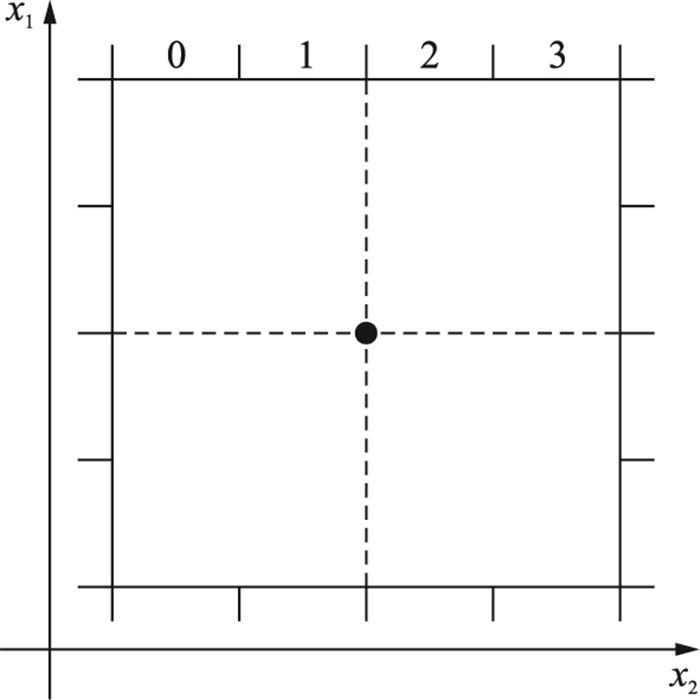
二维表面量化如图 3所示.
当控制器接收到量化结果Q时,控制器可以根据触发条件ϑ和量化区间个数l更新控制器中的模型状态.
当i=I时:
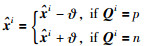
|
(12) |
当i≠I时:
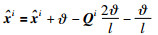
|
(13) |
|
| 图 3 l=4,n=2时表面量化示意图 Figure 3 The surface quantization illustration for l=4, n=2 |
由上文可知,量化器使用的比特数为
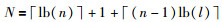
|
(14) |
在N个比特中,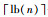
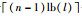
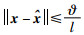
|
(15) |
本节将基于引理1,定量研究动态量化对所考虑的基于模型的事件触发控制系统的影响.首先,针对动态量化器带来的编解码问题,给出了一个基于模型状态的触发条件,其类似于式(4)中的触发条件能够确保系统渐近稳定.其次,将给出系统量化使用的最小比特数,以确保不会在模型状态更新后立刻触发下一次事件,即避免Zeno现象(事件触发间隔无限小)发生.最后,给出事件触发间隔的一个下界.
2.1 基于模型状态的事件触发条件由引理1可知,当系统的触发条件为式(4)时,系统渐近稳定,这里采用的触发条件是关于系统状态x(t)的触发条件.从系统的原理框图 1看到,传感器可以得到完整的系统状态,但控制器不能,所以如果采用基于系统状态的触发条件(4),控制器不能正确译码得到状态误差.由于传感器中也运行一个模型,因此可以用一个关于模型状态的事件触发条件代替式(4)作为事件触发条件,其基于引理2:
引理2 如果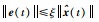
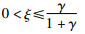
|
(16) |
则有‖e(t)‖≤γ‖x(t)‖.
证明 由范数三角不等式可得:
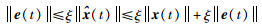
|
(17) |
通过移项可得:
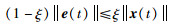
|
(18) |
由式(18)可以推出:
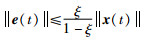
|
(19) |
易知,当ξ满足式(16)时,‖e(t)‖≤γ‖x(t)‖.
由引理2可知,当状态误差满足一个关于模型状态的约束条件时,这个状态误差也满足一个关于系统状态的约束条件.因此,可以将引理1中基于系统状态的触发条件替换为基于模型状态的触发条件.定义:
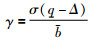
|
(20) |
选择系统的触发条件为
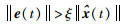
|
(21) |
其中,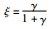
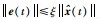
由于每次事件触发后模型状态会更新,式(21)中的触发条件也许会在模型状态更新后马上被满足,这就导致两次触发的时间间隔为0,出现了Zeno现象,这是不可接受的.为避免Zeno现象,下面给出一个量化比特数条件.
引理3 假设均匀量化器将量化区间上每一维划分成l个子区间,当系统触发条件为式(21)时,若满足:
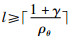
|
(22) |
其中,ρθ∈(0,1),l∈Z+,l>1.则模型状态更新后:
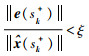
|
(23) |
不会在t=sk+时刻触发式(21)中的事件.
证明 已知式(21)为触发条件.当t=sk-时:
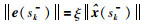
|
(24) |
模型状态的更新方程为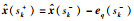
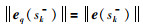
|
(25) |
由范数的三角不等式可以得到:
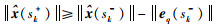
|
(26) |
由式(15)可知,更新后状态误差为
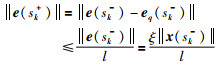
|
(27) |
将式(24)和式(25)代入式(26):
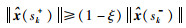
|
(28) |
由式(27)和式(28)得到:
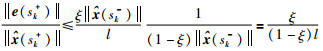
|
(29) |
当l满足式(22)时:
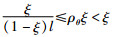
|
(30) |
故式(23)成立.
注1 从式(28)可知,当初始状态不在原点时,在系统收敛过程中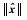
注2 引理3中并没有直接给出量化器使用的比特数下界,但给出了量化器在每一维上量化区间数的下界.根据式(14)可以计算出对应的比特数下界.
2.3 确保系统稳定性的事件触发间隔下界引理3表明事件触发间隔不为0.本节再进一步,给出事件触发间隔的一个下界.
引理4 如果对系统(1)及模型(2),采用式(21)中的触发条件且l满足式(22),那么系统存在一个不为0的最小触发间隔T,即:
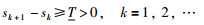
|
(31) |
证明 通过分析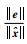
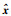
由系统状态方程(1)和模型状态方程(2)可以得到:
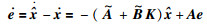
|
(32) |
根据模型误差的上界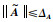
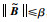
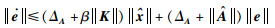
|
(33) |
由模型动态方程(2)可得:
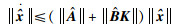
|
(34) |
下面研究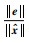
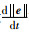
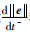
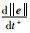
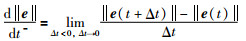
|
(35) |
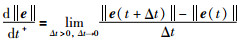
|
(36) |
同理,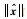
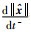
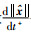
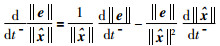
|
(37) |
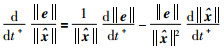
|
(38) |
易知对任意非0的Δt,一定有:
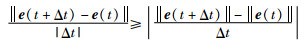
|
(39) |
可以得到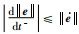
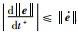
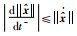
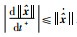
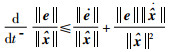
|
(40) |
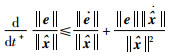
|
(41) |
将式(33)和式(34)代入式(40)、式(41)中:
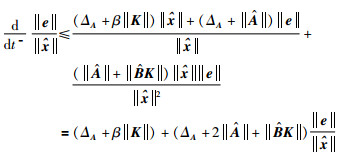
|
(42) |
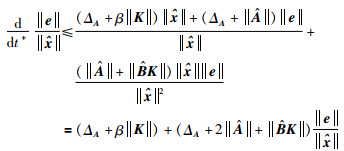
|
(43) |
当t∈[sk,sk+1)时,e和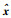
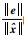
令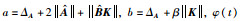
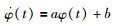
|
(44) |
其初始值为φ(sk)=ρθξ,可得:
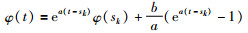
|
(45) |
定义T为φ(T+sk)=ξ的解,可求解得到:
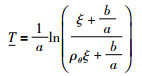
|
(46) |
已知ρθ∈(0,1),所以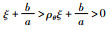
由式(30)可知,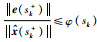
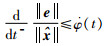
|
(47) |
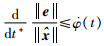
|
(48) |
因此在该时间段,必有:
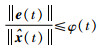
|
(49) |
可以看到函数φ(t)是单调递增函数,因此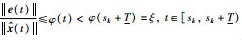
注3 由式(46)可以看到,最小触发间隔与模型和模型误差都相关,同时也与参数ρθ的选取有关,ρθ越小,T越大.由式(15)可知,当ρθ趋近于0时,量化器使用的比特数趋近于无穷,此时该系统接近于不使用量化器时的系统,并且T趋近于一个恒定的值:
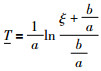
|
(50) |
这个值是不考虑量化时,系统的最小触发间隔的下界.可以看到这个最小触发间隔由模型参数及模型误差决定.当模型误差不存在时,T为无穷,系统只需采样一次.
根据上述引理,最终可以得到一个基于模型的事件触发动态量化控制系统的稳定结论.
定理1 若系统(1)和模型(2)满足引理1中的条件且触发条件为(21),量化器满足式(22),则系统渐近稳定且存在一个大于0的最小触发间隔.
证明 由引理1和引理2可得,当系统触发条件为式(21)时,系统渐近稳定.如果量化器满足引理3的条件,由引理4可以得出系统存在一个大于0的最小触发间隔T.
定理1 总结了上述4个引理,给出了引入动态量化器后的事件触发控制条件及量化比特数下界和系统的最小触发间隔.值得一提的是本文中给出的结果只与近似模型及模型误差上界有关,因此无需得到系统的精确模型,在实际工程中更易实现.
3 仿真结果本文在一个二阶线性系统上进行仿真实验,对定理1进行了验证.所考虑系统的状态方程为
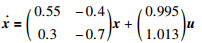
|
(51) |
模型状态方程为
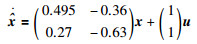
|
(52) |
其中,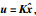
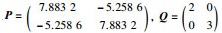
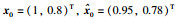
|
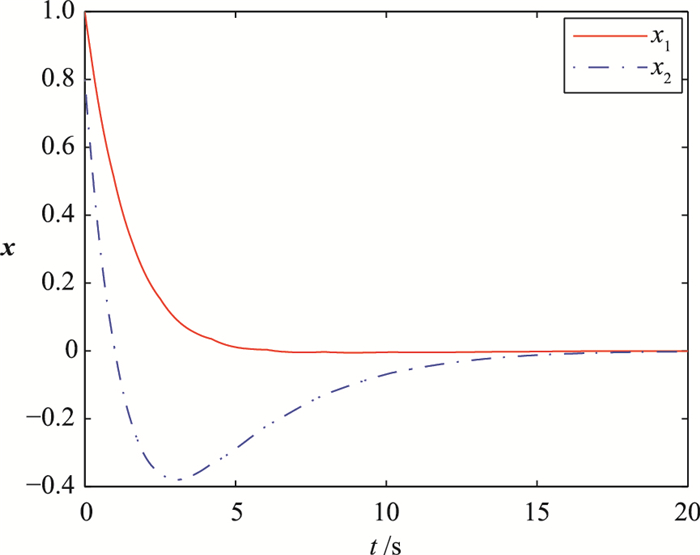
| 图 4 系统状态 Figure 4 The states of the system |
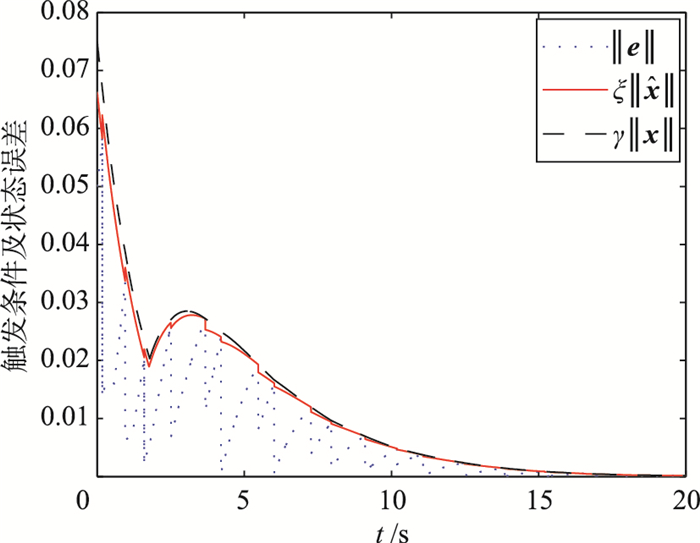
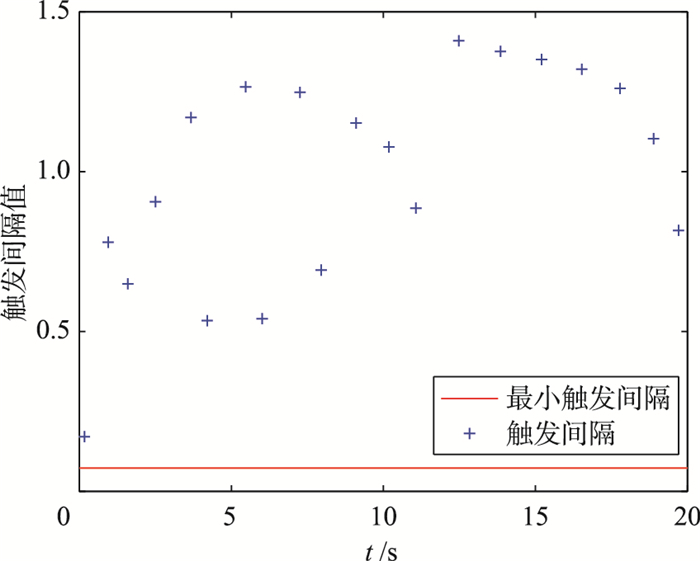
由图 4可见,系统的确渐近稳定.相对于文[20]需要使用无限个比特来量化,本文量化使用的比特数为N=3.图 5中包含了状态误差、事件触发条件的变化情况.可以看到根据引理2给出的基于模型状态条件触发的事件一直小于或等于基于系统状态的事件触发条件,模型状态误差每当等于这个新的触发条件时系统触发采样并更新模型状态.而且,新的触发条件在更新前后存在跳变现象,虽然由于量化误差的存在,更新后状态误差不为0,但采用引理3计算的最小量化比特数可以保证采样后状态误差不会马上触发新的事件.图 6记录了系统的触发间隔,系统一共触发20次,并且所有的触发间隔均大于引理4计算出的最小触发间隔.综上,本文所设计的事件触发动态量化反馈控制策略使用有限比特进行量化并能够保证系统渐近稳定,同时能够避免Zeno现象.
|
| 图 5 触发条件及状态误差 Figure 5 The triggering threshold and the state errors |
|
| 图 6 触发间隔 Figure 6 The inter-sampling time |
本文在原有的基于模型的事件触发控制系统中考虑实际网络带宽的有限性,根据事件触发控制的特性引入了表面量化的均匀量化器,同时对应地设计了新的触发条件使系统具有渐近稳定性;给出了量化器比特数的约束条件,保证了系统存在大于0的最小触发间隔.在文[20]中,使用对数量化器的事件触发控制系统,每次采样时系统需要使用无限比特表示模型误差;而本文通过每次传输有限个比特,最终实现了与其相同的渐近稳定性,在实际工程中更易实现.在今后的研究中,可以在多智能体系统中研究事件触发量化反馈控制策略.
| [1] | Gupta R A, Chow M Y. Networked control system:Overview and research trends[J]. IEEE Transactions on Industrial Electronics, 2010, 57(12): 2527–2535. |
| [2] |
邢江, 关治洪.
网络化控制系统的研究现状与展望[J]. 控制工程, 2006, 13(4): 294–297.
Xing J, Guan Z H. Research progress and prospects of the networked control systems[J]. Control Engineering of China, 2006, 13(4): 294–297. DOI:10.3969/j.issn.1671-7848.2006.04.002 |
| [3] | Yu H, Antsaklis P J. Event-triggered output feedback control for networked control systems using passivity:Achieving L2 stability in the presence of communication delays and signal quantization[J]. Automatica, 2013, 49(1): 30–38. DOI:10.1016/j.automatica.2012.09.005 |
| [4] | Guan Y, Han Q L, Peng C. Event-triggered quantized-data feedback control for linear systems[C]//2013 IEEE International Symposium on Industrial Electronics (ISIE). Piscataway, NJ, USA: IEEE, 2013: 1-6. |
| [5] | Tatikonda S, Mitter S. Control under communication constraints[J]. IEEE Transactions on Automatic Control, 2004, 49(12): 1056–1068. |
| [6] | Fu M, Xie L. Finite-level quantized feedback control for linear systems[J]. IEEE Transactions on Automatic Control, 2009, 54(10): 1165–1170. |
| [7] | Brockett R W, Liberzon D. Quantized feedback stabilization of linear systems[J]. IEEE transactions on Automatic Control, 2000, 45(12): 1279–1289. |
| [8] | Lemmon M. Event-triggered feedback in control, estimation, and optimization[M]. London, UK: Springer Networked Control Systems, 2010: 293-358. |
| [9] | Borgers D P N, Heemels W M. Event-separation properties of event-triggered control systems[J]. IEEE Transactions on Automatic Control, 2014, 59(15): 2644–2656. |
| [10] | Astrom K J, Bernhardsson B M. Comparison of riemann and lebesgue sampling for first order stochastic systems[C]//the 41st IEEE Conference on Decision and Control. Piscataway, NJ, USA: IEEE, 2002: 2011-2016. |
| [11] | Mazo M, Anta A, Tabuada P. An ISS self-triggered implementation of linear controllers[J]. Automatica, 2010, 46(13): 1310–1314. |
| [12] | Mazo M, Tabuada P. Input-to-state stability of self-triggered control systems[C]//the 28th Chinese Control Conference on Decision and Control. Piscataway, NJ, USA: IEEE, 2009: 928-933. |
| [13] | Wang X, Lemmon M D. Event-triggering in distributed networked control systems[J]. IEEE Transactions on Automatic Control, 2011, 56(3): 586–601. DOI:10.1109/TAC.2010.2057951 |
| [14] | Tallapragada P, Cortés J. Event-triggered stabilization of linear systems under bounded bit rates[J]. IEEE Transactions on Automatic Control, 2016, 61(11): 1575–1589. |
| [15] | Lehmann D, Lunze J. Event-based control using quantized state information[J]. IFAC Proceedings Volumes, 2010, 43(26): 1–6. DOI:10.3182/20101206-3-JP-3009.00003 |
| [16] | Li L, Wang X, Lemmon M D. Efficiently attentive event-triggered control systems with limited bandwidth[J]. IEEE Transactions on Automatic Control, 2016, 62(3): 1491–1497. |
| [17] | Garcia E, Antsaklis P J, Montestruque L A. Model-based control of networked systems[M]. Boston, USA: Birkhǎuser, 2014: 135-157. |
| [18] | Tripathy N S, Kar I N, Paul K. Model based robust control law for linear event-triggered system[J]. Asian Journal of Control, 2016, 18(5): 1765–1780. DOI:10.1002/asjc.1276 |
| [19] | Montestruque L A, Antsaklis P J. Static and dynamic quantization in model-based networked control systems[J]. International Journal of Control, 2007, 80(1): 87–101. DOI:10.1080/00207170600931663 |
| [20] | Garcia E, Antsaklis P J. Model-based event-triggered control for systems with quantization and time-varying network delays[J]. IEEE Transactions on Automatic Control, 2013, 58(2): 422–434. DOI:10.1109/TAC.2012.2211411 |



