0 引言
生产实际中,常常需要考察系统在特定频段的性能指标,有时甚至需要在不同频段满足不同的性能指标.因此有限频段问题的研究应运而生[1-2].为解决该问题,学者们提出了频率加权法[3-4],然而由于频率加权函数的复杂度与系统设计指标描述的精确性之间难以平衡,导致该方法的适用范围受限. 2005年,Iwasaki等人基于S-procedure的方法提出了广义KYP引理,真正打开了有限频段问题研究的大门[5-7].基于广义KYP引理的有限频段理论研究已经日益体现出巨大优越性和应用潜力,成为了有限频段问题研究的主流方法.
近年来,对于广义KYP引理的有限频段问题研究拓展到了各个领域,包括开环回路成形[8],滤波器设计[9-10],车辆悬架系统[11-13]等方面.但大多数已有研究都是针对单一模态系统,对于在电力系统、经济系统以及化工系统中广泛存在的多模态混杂系统[14-16]却鲜有研究.虽然文[17]和文[18]考虑了切换系统和马尔可夫跳变系统的有限频段问题,然而由于仅考虑了各个子系统满足有限频段性能指标,而忽略了子系统间产生的切换或跳变对于系统整体性能指标的影响.
因此本文针对这一问题,借鉴文[19]中利用算子理论构造高维空间的思想,将原跳变系统各模态参数进行增广,转换为带有跳变率信息的确定系统,并证明了增广确定系统的李亚普诺夫稳定性以及有限频段性能指标问题等价于原跳变系统,进一步利用广义KYP引理实现原随机跳变系统的多频段多指标控制.与已有方法相比[20],本文所得结果由于考虑了系统跳变瞬间有限频段性能,而不仅仅是各子系统的有限频段性能,因此具有更小的保守性.仿真实例验证了结果的有效性与优越性.
本文中使用了如下标识:NΤ和N*代表了矩阵N的转置和复共轭转置;N=diag{N1,N2,…,Ns}表示了矩阵N是对角线元素为N1,N2,…,Ns、其余位置元素为0的矩阵;为简化书写,使用He{N}来代替N+N*;⊗表示的是Kronecker积.
1 问题描述在给定完备概率空间,考虑连续时间马尔可夫跳变系统:
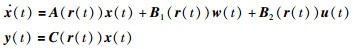
|
(1) |
其中,A(r(t))、B1(r(t))、B2(r(t))、C(r(t))是与模态相关的系数矩阵,x(t)是系统的状态向量,u(t)是控制向量,w(t)是干扰输入,y(t)为被控输出,x0、r0分别代表了系统的初始状态与初始模态.其中,r(t)表征了t时刻系统所处模态i,i∈S,S={1,2,…,s}.为简化书写,系统系数矩阵可简写为:Ai、B1i、B2i、Ci.系统各模态间的转移概率可表示为
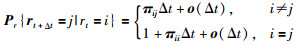
|
其中,Δt>0,o(Δ(t))为Δt的无穷小量,且对于跳变系统的跳变率有:
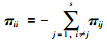
|
(2) |
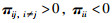
|
(3) |
本文主要针对系统(1),设计如下状态反馈控制器:
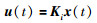
|
使得如下闭环系统:
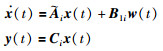
|
(4) |
随机稳定,同时满足以下有限频段性能指标:
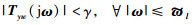
|
(5) |
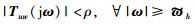
|
(6) |
其中,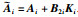
在实现设计目标的过程中,需要使用如下引理:
引理1(广义KYP引理[6]) 对于传递函数为G(λ)=C(λI-A)-1B+D的线性系统,给定对称矩阵Π和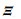
1) 有限频段不等式:
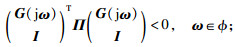
|
2) 存在对称矩阵P,Q>0,且
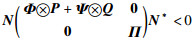
|
其中,ϕ为ω所属频段,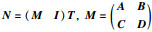
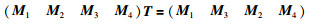
|
注1 在广义KYP引理中,矩阵Φ代表了系统的连续性与离散性,Ψ表征了频段信息,Π刻画了系统需要满足的有限频段性能指标[5].
引理2(Finsler′s Lemma[21]) 对于m∈Rn,对称矩阵
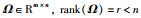
1) 对于任意m≠0且Ωm=0,有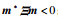
2) 存在Δ∈Rn×m,使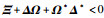
由于跳变系统(4)具有多模态随机马尔可夫跳变特性,其传递函数难以通过系统(4)进行直接描述,故不能直接利用广义KYP引理进行时频域转换.因此,首先借鉴文[19]的思想,将目标闭环系统的随机稳定以及有限频段性能指标充分条件转化为重构确定系统的相应条件,具体见如下定理:
定理1 当确定系统(7)李亚普诺夫渐近稳定,且满足指标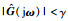
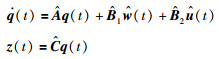
|
(7) |
其中:
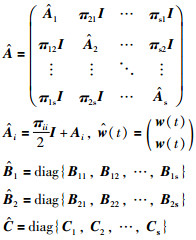
|
证明 针对确定系统(7),考虑状态反馈控制输入:
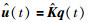
|
其中,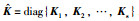
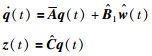
|
(8) |
其中:
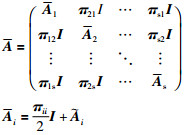
|
对系统(8)取李亚普诺夫函数: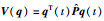
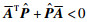
|
(9) |
则式(9)等价于:
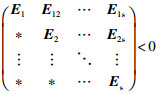
|
(10) |
其中,对角线元素为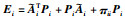
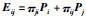
对式(10)右乘
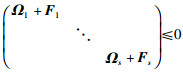
|
(11) |
为节约空间,式(11)中非对角线元素省去,其中:
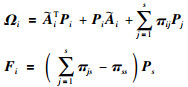
|
可得式(11)中对角线元素满足:
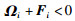
|
(12) |
结合式(3)可得:
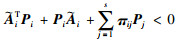
|
(13) |
由文[22]中推论3可知,式(13)意味着原随机跳变系统(4)渐近稳定.
另外,由文[23]可得,系统(7)满足性能指标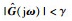
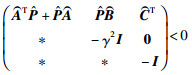
|
(14) |
则利用前文已证部分可得:
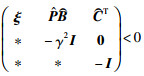
|
(15) |
其中,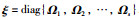
利用Schur补定理,对式(15)进行等价变形得:
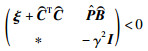
|
以上不等式等价于:

|
(16) |
其中,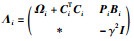
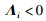
|
(17) |
对于原跳变系统(4)定义:
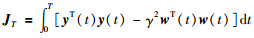
|
则:
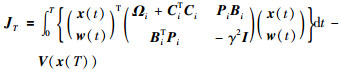
|
则由式(17)可得:
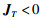
|
(18) |
由此可得|G(jω)| < γ.
因此,通过定理1,本文所考察的有限频段性能指标(5)和(6)转为考察系统(8)的如下性能指标:
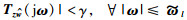
|
(19) |
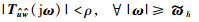
|
(20) |
同时系统(8)还须满足李亚普诺夫渐近稳定性条件,因此得到了如下定理.
定理2 考虑闭环系统(8),给定Ψ、Φ,常矩阵Rl、Rh,性能指标参数γ、ρ以及频率ωl和ωh,若存在Pl=Pl*,Ph=Ph*,Ql=Ql*>0,Qh=Qh*>0,Vl,Vh,W和K等矩阵变量,使以下不等式成立:
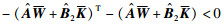
|
(21) |
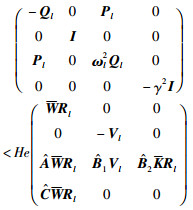
|
(22) |
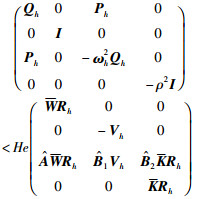
|
(23) |
则系统(8)李亚普诺夫稳定,且满足多频段性能指标(19)和(20),其控制器参数可由下式得到:
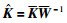
|
其中:
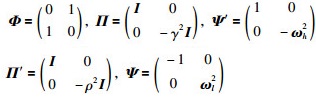
|
证明 根据引理1,式(19)等价于:
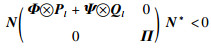
|
(24) |
其中:
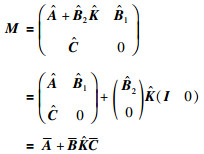
|
利用引理2,上式可转化为
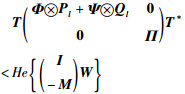
|
(25) |
使问题可解,将乘子W进行如下限制:
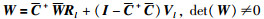
|
(26) |
式(25)可以改写为
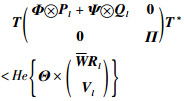
|
(27) |
其中:
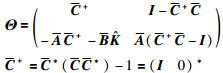
|
则式(27)转化为
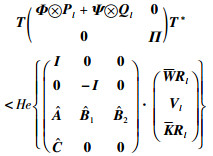
|
(28) |
即条件(22).
同理可证,条件(23)可推得闭环系统(8)满足性能指标(20).
令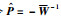
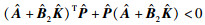
|
(29) |
因此,闭环系统(8)李亚普诺夫渐近稳定,即原跳变系统(4)渐近稳定.
注2 由于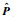
进一步,根据定理2的结果,可以对不同频段下的性能指标进行如下优化:
定理3 已知Ψ,Φ,常矩阵Rl、Rh,性能指标参数γ以及频率ωl和ωh,若存在Pl=Pl*,Ph=Ph*,Ql=Ql*>0,Qh=Qh*>0,Vl,Vh和W等矩阵变量,可以通过以下算法求解得到系统的多频段状态反馈控制器参数Ki以及最优性能指标ρ:
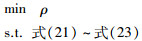
|
考虑文[5]中所用的弹簧系统,其弹性常量并非固定不变,而是在一定范围内随机变化,呈现出马尔可夫跳变特性,因此可将其建立为具有如下系统参数的两模态跳变系统模型:
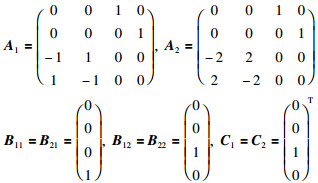
|
其跳变率矩阵为
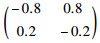
|
利用定理1,可得增广线性系统的系数矩阵为

|
取Rl=(0 0 I 0),Rh=(I 0 0 0),系统初始状态为x0=(0.50.21.51.4)T,γ=2,ωl=2,ωh=5,干扰信号为w(t)=0.2 sin πt,结合定理3,利用Matlab线性矩阵不等式工具箱求解得到控制器参数为
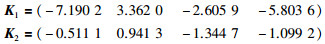
|
并得到ρmin=1.650 6.
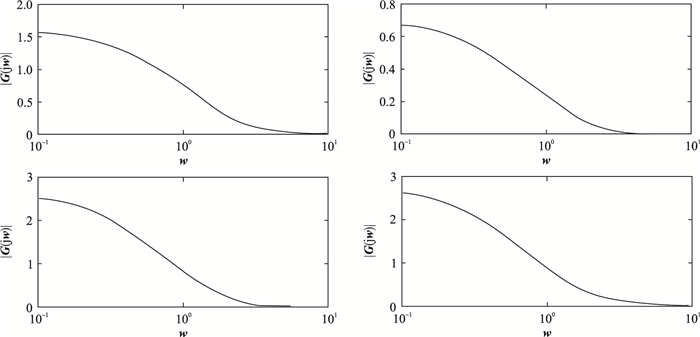
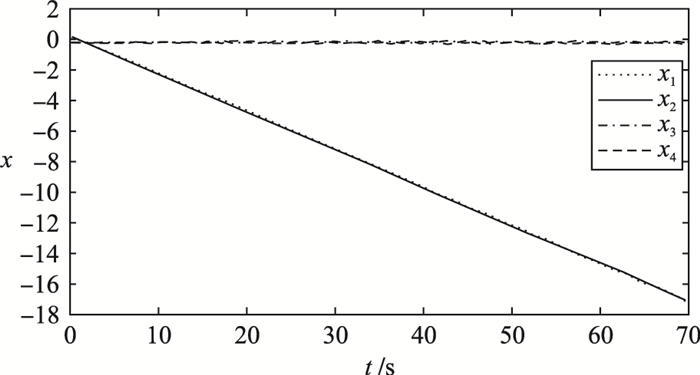
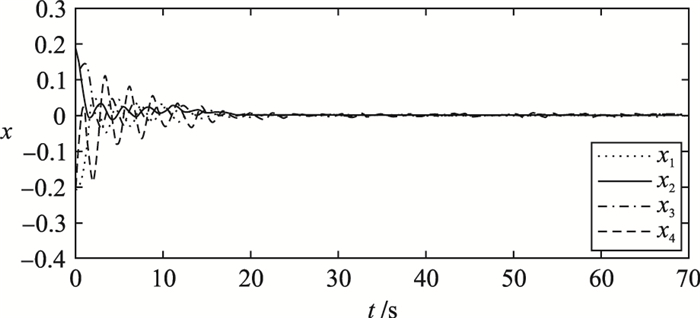
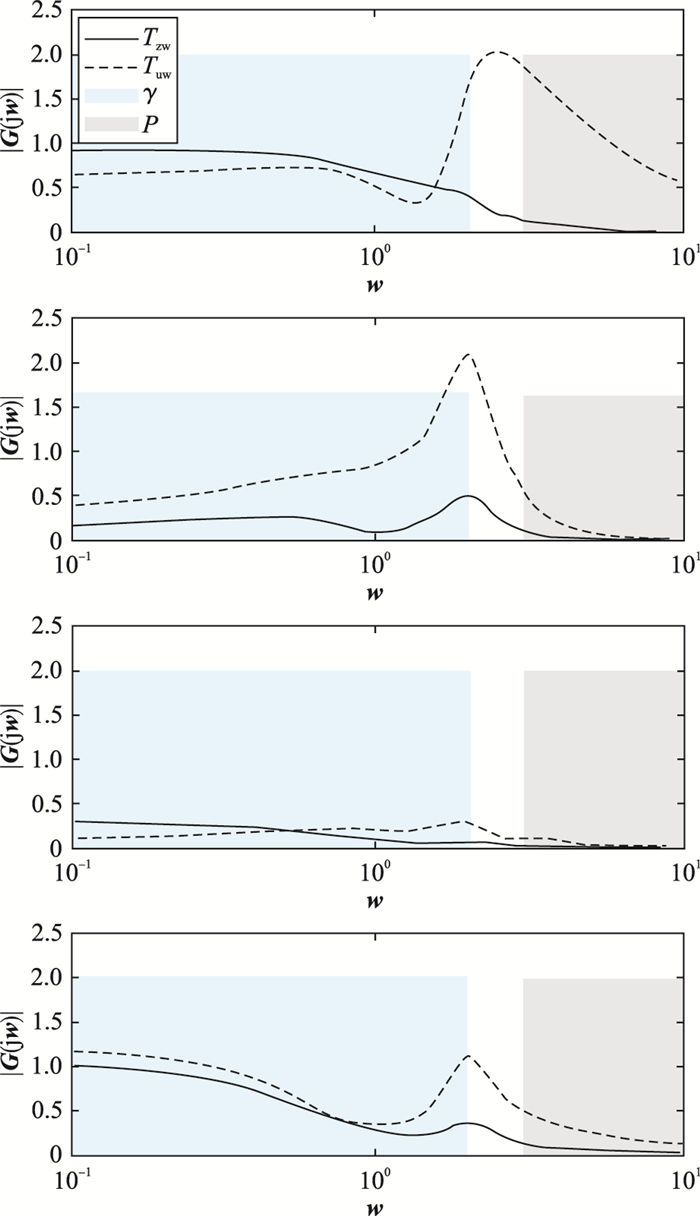
将所得参数代入原跳变系统(1),并绘制出其状态响应曲线以及幅频特性图. 图 1和图 2所示为开环跳变系统状态响应曲线以及闭环系统状态响应图.显然可以看到通过转化后系统所求解的控制器对于原跳变系统的有效性. 图 3显示的是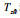
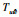
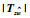
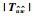
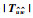
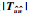
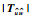
|
| 图 1 开环系统状态响应曲线 Figure 1 The state response curve of the open-loop system |
|
| 图 2 闭环系统状态响应曲线 Figure 2 The state response curve of the closed-loop system |
|
图 3 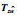 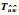 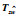 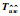 |
在相同条件下,分别调整ωl和ωh的大小,得到表 1.由表 1可知,ωh=6不变时,将ωl慢慢减小到ωl=2,最优指标ρ也逐渐减小.当ωl=2时,将ωh慢慢减小到ωh=ωl=2,最优指标ρ逐渐增大.当ωh=ωl=2时,此时相当于全频段,ρ最大.由此可见,频段越窄,使被控系统实现设计目标所付出的控制能量越少.
| ωl/Hz | ωh/Hz | ρ |
| 5 | 6 | 1.974 6 |
| 4 | 6 | 1.755 4 |
| 3 | 6 | 1.739 5 |
| 2 | 6 | 1.622 1 |
| 2 | 5 | 1.650 6 |
| 2 | 4 | 1.815 3 |
| 2 | 3 | 1.971 4 |
| 2 | 2 | 3.346 2 |
此外,在相同参数下利用文[20]的结果求解被控系统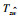
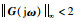
本文主要针对随机马尔可夫跳变系统的传递函数难以描述的问题,将跳变系统的状态进行增广,得到系数参数矩阵带有跳变率信息的增广确定系统,然后利用广义KYP引理将表征多频段性能指标的频域不等式转化为线性矩阵不等式,求解得到使原随机跳变系统李亚普诺夫稳定并满足多频段多性能指标的状态反馈控制器参数.本文从多频域角度降低了跳变系统的控制器设计保守性,未来研究将结合有限时间理论,从时间与频率两个不同的尺度,研究马尔可夫跳变系统的多频段多指标问题.
| [1] | Iwasaki T, Meinsma G, Fu M. Generalized S-procedure and finite frequency KYP lemma[J]. Mathematical Problems in Engineering, 2000, 6(2/3): 1465–1466. |
| [2] | Zhang S, Wang Z, Ding D, et al. On design of robust fault detection filter in finite-frequency domain with regional pole assignment[J]. IEEE Transactions on Circuits & Systems Ⅱ:Express Briefs, 2015, 62(4): 382–386. |
| [3] |
吴敏, 桂卫华, 何勇.
现代鲁棒控制[M]. 长沙: 中南大学出版社, 2006.
Wu M, Gui W H, He Y. Modern robust control[M]. Changsha: Central South University Press, 2006. |
| [4] | Zhou K, Doyle J C, Glover K. Robust and optimal control[M]. Upper Saddle River, NJ, USA: Prentice Hall, 1996. |
| [5] | Iwasaki T, Hara S, Yamauchi H. Dynamical system design from a control perspective:Finite frequency positive-realness approach[J]. IEEE Transactions on Automatic Control, 2003, 48(8): 1337–1354. |
| [6] | Iwasaki T, Hara S. Robust control synthesis with general frequency domain specifications: Static gain feedback case[C]//2004 American Control Conference. Piscataway, NJ, USA: IEEE, 2004: 4613-4618. |
| [7] | Iwasaki T, Hara S. Generalized KYP lemma:Unified frequency domain inequalities with design applications[J]. IEEE Transactions on Automatic Control, 2005, 50(1): 41–59. |
| [8] | Hara S, Iwasaki T, Shiokata D. Robust PID control using generalized KYP synthesis:Direct open-loop shaping in multiple frequency ranges[J]. IEEE Control Systems, 2006, 26(1): 80–91. DOI:10.1109/MCS.2006.1580156 |
| [9] | Ding D W, Yang G H. Fuzzy filter design for nonlinear systems in finite-frequency domain[J]. IEEE Transactions on Fuzzy Systems, 2010, 18(5): 935–945. |
| [10] | Lee D H. An improved finite frequency approach to robust H∞ filter design for LTI systems with polytopic uncertainties[J]. International Journal of Adaptive Control and Signal Processing, 2013, 27(11): 944–956. |
| [11] | Sun W, Zhao Y, Li J, et al. Active suspension control with frequency band constraints and actuator input delay[J]. IEEE Transactions on Industrial Electronics, 2012, 59(1): 530–537. DOI:10.1109/TIE.2011.2134057 |
| [12] | Wang R, Jing H, Yan F, et al. Optimization and finite-frequency H∞ control of active suspensions in in-wheel motor driven electric ground vehicles[J]. Journal of the Franklin Institute, 2015, 352(2): 468–484. DOI:10.1016/j.jfranklin.2014.05.005 |
| [13] | Sun W, Li J, Zhao Y, et al. Vibration control for active seat suspension systems via dynamic output feedback with limited frequency characteristic[J]. Mechatronics, 2011, 21(1): 250–260. DOI:10.1016/j.mechatronics.2010.11.001 |
| [14] | Ezzine J, Haddad A H. Controllability and observability of hybrid dynamic[J]. International Journal of Control, 1989, 49(6): 2045–2055. DOI:10.1080/00207178908559761 |
| [15] | Van de Schaft A, Schumacher H. An introduction to hybrid dynamical systems[M]. Berlin, Germany: Springer-Verlag, 2000. |
| [16] | Liu J, Teel A R. Invariance principles for hybrid systems with memory[J]. Nonlinear Analysis Hybrid Systems, 2016, 21: 130–138. DOI:10.1016/j.nahs.2015.08.003 |
| [17] | Zhao X G, Li J, Ye D. Fault detection for switched systems with finite-frequency specifications[J]. Nonlinear Dynamics, 2012, 70(1): 409–420. DOI:10.1007/s11071-012-0464-5 |
| [18] |
赵长钟, 栾小丽, 刘飞.
基于有限频段的Markov跳变系统有限时间H∞滤波[J]. 控制理论与应用, 2015, 32(3): 406–412.
Zhao C Z, Luan X L, Liu F. Finite-time H∞ filtering for Markov jump systems in finite frequency domain[J]. Control Theory and Application, 2015, 32(3): 406–412. |
| [19] | Costa O L V, Fragoso M D, Marques R P. Discrete-time Markov jump linear systems[M]. Berlin, Germany: Springer Science & Business Media, 2006. |
| [20] |
周超洁, 栾小丽, 刘飞.
跳变系统在给定时间内的有限频段H∞控制[J]. 控制理论与应用, 2016, 33(2): 251–256.
Zhou C J, Luan X L, Liu F. Finite frequency H∞ control for jump systems over given time interval[J]. Control Theory and Application, 2016, 33(2): 251–256. |
| [21] | Skelton R E, Iwasaki T, Grigoriadis D E. A unified algebraic approach to control design[M]. Boca Raton, FO, USA: CRC Press, 1997. |
| [22] | Li L, Ugrinovskii V A. On necessary and sufficient conditions for H∞ output feedback control of Markov jump linear systems[J]. IEEE Transactions on Automatic Control, 2006, 52(7): 1287–1292. |
| [23] |
俞立.
鲁棒控制:线性矩阵不等式处理方法[M]. 北京: 清华大学出版社, 2002.
Yu L. Robust control:linear matrix inequality approach[M]. Beijing: Tsinghua University Press, 2002. |