0 引言
PID控制器之所以能被广泛使用,是因为其简单的结构和令人满意的鲁棒性[1-2].然而,PID控制器的性能过度依赖于控制器的参数[3].尽管理想的PID控制器只有3个参数调整,但是如何有效地确定这3个参数是一个挑战[4].
经过几十年发展,出现了许多用来优化PID控制器参数的方法.典型的方法包括Ziegler-Nichols阶跃响应法[5-6],相位裕度法[7-8]等.但是,当调整的PID控制器处在复杂的操作情况(如,多约束条件)时,典型的优化方法很难克服新的理论挑战.在这种情况下,学者们提出了使用智能优化算法的方法来优化PID控制器参数.例如:蚁群优化(ACO)神经网络(NN)算法,粒子群优化(PSO),差分进化(DE),遗传算法(GA)等.此外,杨等[9]提出了使用改进的粒子群优化算法搜索PID控制器的最优参数. Jin等[10]使用NPSO算法获得一阶滞后对象的增量式PID控制器的参数.唐等[11]使用多Agent混沌粒子群得到鲁棒的PID控制器的参数.
近年来,Yang教授和Deb教授[12]报道了一种新的智能优化算法(即,布谷鸟算法),该算法基于布谷鸟的寄生育雏模式,并将该算法用来解决静态测试函数的优化问题.此外,上述布谷鸟搜索理论已成功应用在各个优化领域.例如:人群疏散多目标优化问题中的应用[13],车辆配送路径寻优问题[14],梯级水库优化问题[15]等.然而,应该注意的是,基本的CS算法似乎很难在获得搜索收敛速度快的同时还能得到全局最优解.为了克服这一弱点,学者们提出了一些修改CS算法:Huang等[16]提出Chaos-enhanced CS优化算法,利用混沌序列来初始化布谷鸟初始巢穴位置,来改进步长策略和边界问题的处理. Jia等[17]提出了一种改进的布谷鸟搜索(ICS)优化KFCM模型的参数.
然而,应用CS算法来优化PID控制器参数的学术研究还相当稀少.此外,针对带多约束的不稳定时滞对象没有一个一般的PID控制器优化方法.另一方面,在大部分的工业过程中,不稳定极点[18]和多约束条件[19]是常见的.在这样的情况下,我们首先提出一个新的改进的布谷鸟搜索算法来解决带多个约束的不稳定时滞对象的PID控制器整定问题.该算法基于布谷鸟搜索算法和非线性随机直接搜索算法,并使用一种新的基于t分布的随机序列.通过仿真研究,验证了该算法的有效性.
1 问题描述 1.1 PID控制器在理想的情况下,PID的形式可以是[2]:
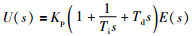
|
(1) |
其中,Kp、Ti、Td、Gc(s)=1/(1+Tf(s))和E(s)分别表示比例因子、积分时间、微分时间、PID控制器的输出和系统偏差.然而,在实际情况下,理想的微分作用可以很容易地引入高频干扰.同时,理想的微分时间带来的缺点是可以克服的.通过加入一阶滤波器(Gf(s)=1/(1+Tf(s)))对增量式PID控制器进行补偿.这样,实际的PID控制器形式可以描述为
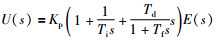
|
(2) |
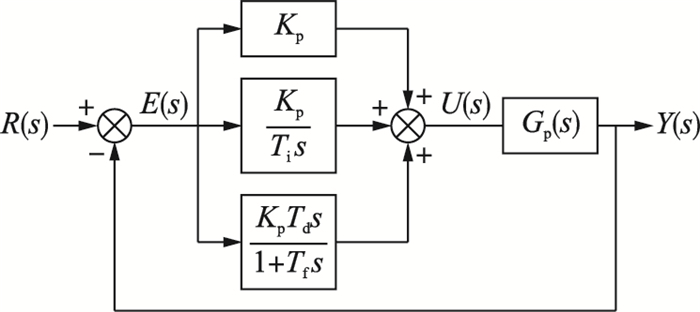
图 1展示了PID控制系统的方块图.其中,控制对象为Gp(s),控制器为Gc(s),控制对象Gp(s)和控制器Gc(s)组成一个闭环控制系统.
|
| 图 1 PID控制系统方块图 Figure 1 The block diagram of the PID control system |
众所周知,传感器输出信号的一般范围是4~20 mA.在现实工业,为了保护传感器,传感器的这个限制是不可避免的.另外,控制器的输出信号的一般范围是0~100,因为这是一般控制阀门固有的限制.因此,研究处理多个约束问题的方法具有很重要的现实意义.
本文采用罚函数方法[3]处理多约束问题.具体来说,通过把约束优化问题转移到智能优化算法的目标函数上,使多约束问题简化为无约束问题.这样,新的综合的目标函数可以表示为
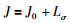
|
(3) |
其中,J0是一个传统的目标函数.一般的J0是积分类型的指标函数,例如:绝对误差的积分(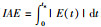
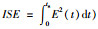
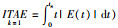
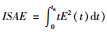
1) Lσ=λ0·|min(0,σ-σ)|,其中设定的一个性能目标σ有一个上限边界σ,λ0是惩罚因子,该惩罚因子是一个极大的正数(例如:λ0=106).在本文中,综合目标函数的函数值越小,表明系统的性能越好.这样,当σ>σ时,Lσ=λ0·|min(0,σ-σ)|是一个很大的正数.根据J=J0+Lσ,目标函数J的值是一个很大的正数.这就意味着算法搜索到的这个解集会被抛弃,因为它的一项性能目标σ已经超出了设定的上限边界σ.
2) Lσ=λ0·|min(0,σ-σ)|,其中设定的一个性能目标σ有一个下限边界σ,λ0是惩罚因子,该惩罚因子和上面一样也是一个极大的正数(例如:λ0=106).这样,当σ < σ时,Lσ=λ0·|min(0,σ-σ)|是一个很大的正数.根据J=J0+Lσ,目标函数J的值是一个很大的正数.这就意味着算法搜索到的这个解集会被抛弃,因为它的一项性能目标σ已经超出了设定的下限边界σ.
举个例子,假设传统的目标函数和惩罚函数分别是IAE和Lσ=λ0·|>min(0,σ-σ)|,综合的目标函数就是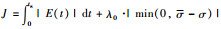
据报道非高斯分布已经在很多领域被使用[3].拉普拉斯分布、威布尔分布,混合高斯分布和t分布是典型的非高斯分布.在本文中,我们使用基于t分布的随机序列来初始化智能优化算法的初始种群.同时,t分布相应的概率密度函数模型可以给出如下:
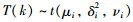
|
(4) |
其中,t(μi,δi2,νi)表示一种普通的单变量学生t分布,μi=0表示位置参数. δi2是方差,νi是自由度.有两个特殊的情况:当νi=1或者νi=∞时,相应的t分布将分别转化为柯西分布或者高斯分布.
非线性随机直接搜索算法(NLJ)是一种随机搜索算法[10].该算法已成功应用于各种识别问题,因为它具有良好的搜索性能和简单的结构.对于每次迭代,更新公式可以如下所示:
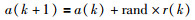
|
(5) |
其中,a(k)是当前迭代次数的解,k表示迭代变量.非线性部分r(k)为NLJ算法的核心部分,可以表示为
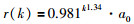
|
(6) |
其中,0.981k1.34表示收敛因子,a0是初始值.然而,NLJ算法的缺点是最优结果太依赖于初始值a0了.因此,为了得到全局最优解,初始值可以由其他的全局优化算法确定好,如粒子群优化算法(PSO)、差分进化算法(DE)、布谷鸟搜索算法(CS).
2 布谷鸟算法布谷鸟算法是Yang教授和Deb教授于2009年联合提出的,该算法模拟布谷鸟寄生育雏的生物规律,获得了很好的优化效果.算法的搜索流程如下所示:
| Procedure Cuckoo Search algorithm: |
| Begin |
| 1. Initialization:initialize the individuals x,the population number N,the parameter pa,and the max generation kmax. |
| 2. Evaluate the fitness value for the individuals x,and set current generation k=1. |
| 3. While (k < kmax) or (stop condition) |
| 4. Obtain new solution randomly by Levy flights; |
| 5. Evaluate fitness Fi for the new solution; |
| 6. Choose a solution of fitness Fj among the N population randomly. |
| 7. If (Fi> Fj) |
| 8. Replace j by the new solution; |
| 9.End if |
| 10.A fraction (pa) of worse nests is abandoned and new ones are built; |
| 11.Keep the best solution; |
| 12.Rank the solution and find the current best; |
| 13.Update the generation number k=k+1. |
| 14.End while |
| End |
正如布谷鸟算法的流程所示,新的解是通过莱维飞行随机游走得到的.这样算法的位置更新方程可以描述成:
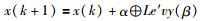
|
(7) |
其中,x(k+1)是第(k+1)次迭代时的解,α是步长,⊕表示乘法,Le′vy(β)表示莱维分布函数.有关基本布谷鸟的更多详细的信息可以阅读参考文[12].
3 基于改进布谷鸟算法的PID控制器参数整定本文基于非线性随机直接搜索算法(NLJ)和t分布序列(如方程4所示),提出了一种新的改进的布谷鸟算法.具体来说,该改进算法使用t分布序列初始化算法的初始种群,采用NLJ算法增强局部搜索能力,改进了边界处理的策略.下面给出了这个改进过程的细节:
3.1 改进的布谷鸟搜索算法 3.1.1 新的改进的搜索策略基本布谷鸟算法的流程可以简单地看成两个部分:
第1部分:使用莱维飞行产生下一代新解:
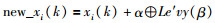
|
(8) |
第2部分:为了确保种群的多样性,按一定概率进行突变:
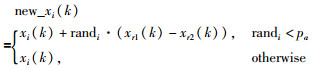
|
(9) |
在方程(9)和方程(10)中,xi(k)是第k次迭代的解,new_xi(k)是新解,α是步长,⊕表示乘法,Le′vy(β)是莱维分布函数,xr1(k)和xr2(k)表示在第k次迭代中随机的两个解. r1、r2和randi是随机数,pa是突变概率.
然而,许多研究已经报道,进一步优化当前的最优解,智能优化算法的性能可以被有效地改善.基于基本的CS算法,我们提出一种新颖的搜索方法,该算法结合全局搜索表现优秀的CS算法和局部搜索表现优秀的NLJ搜索算法.更具体地说,对上述第2部分的变异规则,我们取代传统公式提供的变异操作的公式,而采用的是随机搜索算法(NLJ)提供的非线性部分的变化策略.这样,第2部分可以改进为
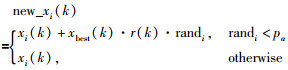
|
(10) |
这里,r(k)是比例因子,确定算法的搜索范围.根据NLJ算法,标准的r(k)可以描述为
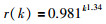
|
(11) |
其中,k表示迭代变量,0.981k1.34表示收敛因子.
3.2 使用t分布序列初始化种群在基本布谷鸟算法中,初始种群可以描述为
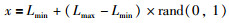
|
(12) |
但是,在改进的布谷鸟搜索算法中,初始种群被设置成
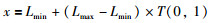
|
(13) |
其中,x初始种群变量,Lmin表示下限边界,Lmax表示上限边界,rand(0,1)表示正态分布随机数,T(0,1)是t分布随机数.值得注意的是,rand(0,1)和T(0,1)都是范围为(0,1)数.关于如何获取T(0,1)可以参考备注1.
3.3 使用t分布序列改进边界处理策略在基本布谷鸟搜索算法,处理搜索边界的策略是:超出边界的解将被设置为的边界值.在这种情况下,边界方程可以表示为

|
(14) |
其中,Lmax和Lmin分别是上边界和下边界.
在改进的布谷鸟算法中,新的策略是把t分布序列应用到边界处理策略上.具体地,把超出边界的解重新设置为基于t分布序列的随机值,这样就可以避免过多的解集中在边界上而影响搜索性能.在这种情况下,新的边界方程可以表示为

|
(15) |
根据方程(15),当一个解飞出了边界,新的策略下,这个解将被设置成一个范围在[Lmin,Lmax]之间的解.同样的,关于如何获取T(0,1)可以参考备注1.
备注1 依据方程(4),首先可以得到一个t分布序列{T(N)},该t分布序列的数据长度和初始种群的大小相同.其次,假定Tmax:=max({T(N)})和Tmin:=min({T(N)}),将[Tmin,Tmax]线性映射到范围为[0, 1]上就得到了一个归一化的t分布序列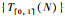
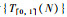
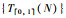
因此,通过结合基本布谷鸟搜索算法和上述3个修改的部分,改进后的布谷鸟搜索算法的流程可以描述如下:
| Procedure of the modified cuckoo search algorithm |
| Begin |
| //初始化程序,使用t分布序列初始化种群 |
| 1. Initialization:use the t-distribution sequence to initialize the individualsx,the population number N,the parameter pa,the max iteration kmax. |
| 2. Set iteration variable k=1,and evaluate the fitness value of x. |
| //使用莱维飞行产生新解 |
| 3. While (k < kmax) |
| 4. For i=1 to Ndo |
| 5. new_xi(k)=xi(k)+α⊕Le′vy(β) |
| 6. End |
| 7. For i=1 to N do |
| 8. Evaluate the fitness of new_xi(k) |
| 9. If new_xi(k) is better than xi(k) |
| then |
| 10. xi(k)=new_xi(k) |
| 11. End if |
| 12.End for |
| //用新的改进的搜索策略(3.1.1所示),进一步优化 |
| 13.For i=1 to N do |
14.new_xi(k)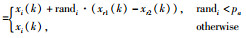 |
| 15.End |
| 16.For i=1 to N do |
| 17. Evaluate the fitness of new_xi(k) |
| 18. If new_xi(k) is better than xi(k) |
| then |
| 19. xi(k)=new_xi(k) |
| 20. End if |
| 21.End for |
| //记录得到的最优解 |
| 22.Memorize the best solution achieved so far |
| 23.k=k+1 |
| 24.End while |
| End |
PID控制器的优化问题,就是通过最小化适应度函数得到一组最优PID参数.本文提出一种改进的布谷鸟优化算法来解决多约束情况下不稳定时滞对象的PID控制器参数整定问题.与此同时,采用罚函数法来处理多约束问题,把多约束问题转化为无约束问题.
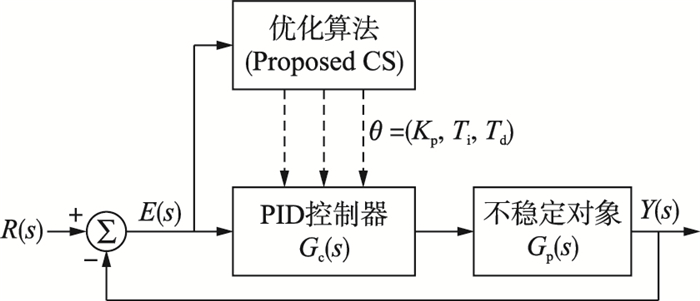
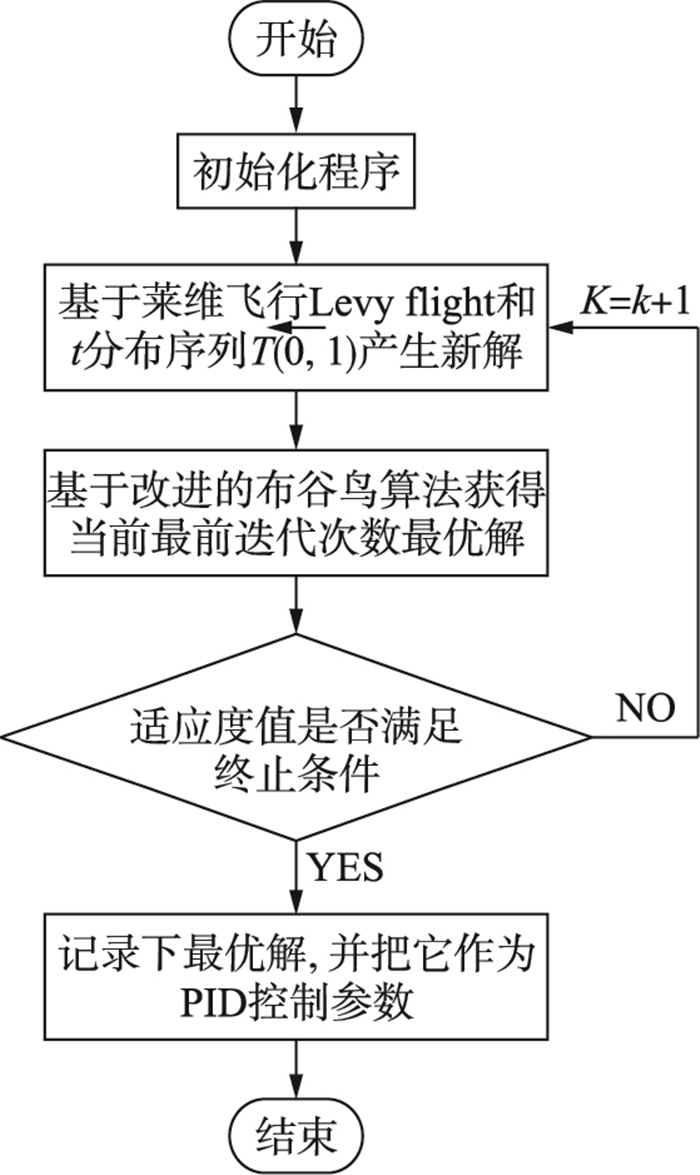
在图 2中,PID控制器Gc(s)和不稳定的对象Gp(s)构成一个闭环控制系统.根据特定的目标函数(如式(3)所示):J=J0+Lσ,我们使用所提出的改进的布谷鸟优化算法来搜索PID控制器参数.通过最小化适应度函数J可以得到最合适的参数.参数调优的流程图如图 3所示,整定的步骤如下:
|
| 图 2 PID控制器参数整定的方块图 Figure 2 Block diagram of the PID controller parameters tuning |
|
| 图 3 参数整定的流程图 Figure 3 The flowchart of the parameters tuning procedure |
步骤1 算法初始化,按照提出的参数初始化方法,设定初始化种群的大小为N,初始种群用x0表示.设定kmax为总的迭代搜索次数,设定搜索计数变量k=1.
步骤2 用莱维飞行策略和t分布序列,产生新的解.
步骤3 评估特定的适应度函数J,通过使用文中提出的改进布谷鸟算法获得当前迭代中的最优解.
步骤4 如果适应度函数值f达到终止条件(或k=kmax),就停止程序,并记录好最优解作为PID控制器的参数;否则,增加k为k+1,返回步骤2继续迭代.
4 仿真在本节中,选用了3个实验进行仿真研究.我们可以通过评估PID控制器的优化性能比较所提出的方法与其它智能优化算法(如PSO,CS和ICS[3])的优劣.在每个实验中,我们使用相同的适应度函数来确保公平的比较. 表 1显示了这些方法的初始化参数设置.此外,每个仿真实例都进行独立的10次试验以确保PID控制器整定的鲁棒性.
| 项目 | 种群大小(N) | 总的迭代次数(kmax) | 变异概率(pa) | 步长[αmin,αmax] | 边界[Lmin,Lmax] |
| 例1 | 200 | 50 | 0.25 | [0.1,0.5] | [0.1.10] |
| 例2 | 200 | 50 | 0.25 | [0.1,0.5] | [0.1,10] |
| 例3 | 200 | 50 | 0.25 | [0.1,0.5] | [0.1,10] |
考虑一个一阶加时滞不稳定对象[20]:
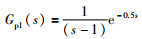
|
(16) |
其中,时滞时间τ为0.5.
在PID控制器的设计中,控制系统的一般约束为对象的产出和控制器的输出.根据系统的特定需求,这个例子的约束可以表示为
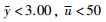
|
(17) |
其中,y表示对象输出的最大值,u表示控制器输出的最大值.此外,在这个仿真例子中,综合目标中的传统目标函数部分为IAE性能指标.这样,综合目标函数可以描述为
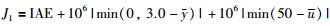
|
(18) |
通过仿真实践,本文使用一个特定的t分布模型(如式(19)所示)来产生t分布序列.该模型也将应用于接下来的仿真实例中.
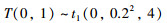
|
(19) |
在式(19)中,表示原始的t分布模型的均值是0,标准差为0.2,自由度为4.根据备注1可以获得需要的t分布序列T(0,1).
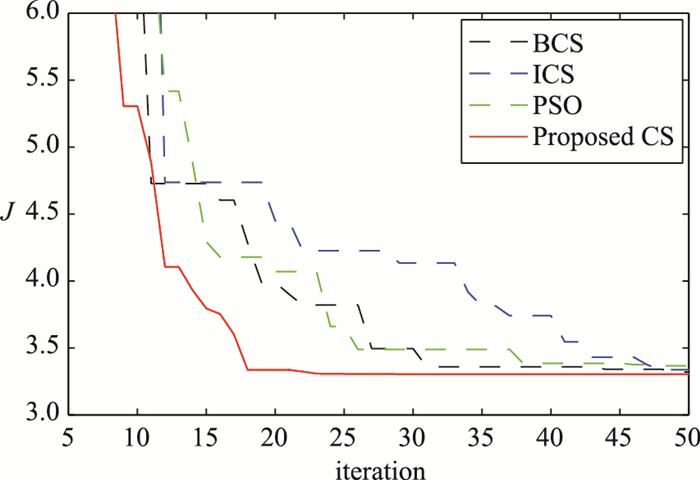
图 4给出了在PSO,CS,ICS以及改进的CS这4个不同智能优化算法下综合性能目标J1的收敛特性. 表 2展示了在不同算法不同次试验下的综合目标J1的值. 表 3给出了在随机一次试验中,不同优化算法下整定得到的参数以及系统的最大超调量Mp、上升时间tr、调整时间ts、稳态误差ess.通过图 4和表 2、表 3的比较,很容易看到,所提出的算法可以提供更合适的控制器参数.
|
| 图 4 例1中基于不同PID整定方法下的收敛性能曲线 Figure 4 The convergence curves by using different PID tuning methods in Example 1 |
| Method | Proposed CS | CS | PSO | ICS |
| 1 | 3.359 8 | 3.411 8 | 3.044 1 | 3.101 9 |
| 2 | 3.499 2 | 3.357 2 | 3.517 0 | 3.319 9 |
| 3 | 2.904 2 | 3.502 2 | 3.060 2 | 3.424 1 |
| 4 | 3.414 8 | 3.065 2 | 3.040 1 | 3.706 4 |
| 5 | 3.429 9 | 2.983 7 | 3.752 5 | 3.149 7 |
| 6 | 3.635 7 | 3.143 7 | 3.560 8 | 3.455 0 |
| 7 | 3.656 7 | 3.530 6 | 3.376 8 | 3.426 7 |
| 8 | 2.906 0 | 3.468 1 | 3.172 2 | 3.348 1 |
| 9 | 2.918 9 | 3.281 8 | 3.358 1 | 3.788 9 |
| 10 | 3.302 8 | 3.318 0 | 3.365 5 | 3.336 9 |
| Mean | 3.255 7 | 3.306 2 | 3.324 7 | 3.405 8 |
| Algorithm | Kp | Ki | Kd | J1 | Mp | tr | ts | ess |
| PSO_PID | 2.229 5 | 2.602 2 | 0.185 9 | 3.365 5 | 2.690 0 | 1.800 0 | 4.200 0 | 1.000 0 |
| BCS_PID | 2.221 6 | 2.497 3 | 0.191 2 | 3.318 0 | 2.666 0 | 1.800 0 | 4.300 0 | 1.000 0 |
| ICS_PID | 2.248 4 | 2.505 3 | 0.195 9 | 3.336 9 | 2.668 0 | 1.900 0 | 4.600 0 | 1.000 0 |
| Proposed CS_PID | 2.229 8 | 2.442 1 | 0.196 8 | 3.302 8 | 2.665 0 | 1.800 0 | 4.000 0 | 1.000 0 |
考虑一个二阶加时滞不稳定对象[21]:
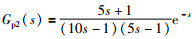
|
(20) |
其中,时滞时间τ为1.
在PID控制器的设计中,控制系统的一般约束为对象的产出和控制器的输出.根据系统的特定需求,这个例子的约束可以表示为
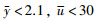
|
(21) |
这样,综合目标函数可以描述为
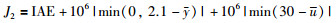
|
(22) |
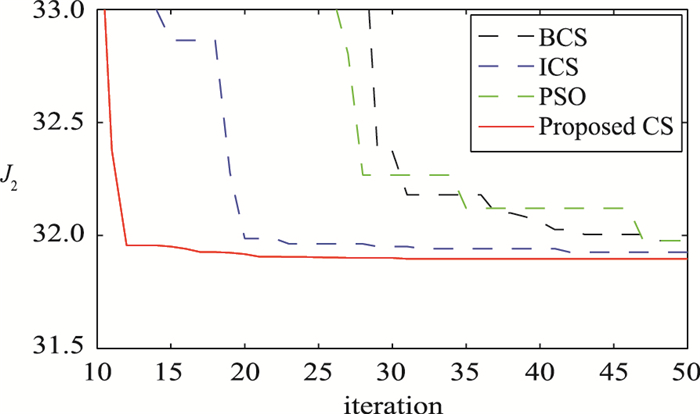
图 5给出了在PSO,CS,ICS以及改进的CS这4个不同智能优化算法下综合性能目标J2的收敛特性. 表 4展示了在不同算法不同次试验下的综合目标J2的值. 表 5给出了在一次随机试验中,不同优化算法下整定得到的参数以及系统的最大超调量Mp、上升时间tr、调整时间ts、稳态误差ess.通过图 5和表 4、表 5的比较,很容易看到,所提出的算法比其他算法更有效.
|
| 图 5 例2中基于不同PID整定方法下的收敛性能曲线 Figure 5 The convergence curves by using different PID tuning methods in Example 2 |
| Method | Proposed CS | CS | PSO | ICS |
| 1 | 31.881 5 | 31.903 4 | 32.897 0 | 31.905 8 |
| 2 | 31.940 8 | 31.910 6 | 31.894 2 | 32.098 3 |
| 3 | 31.807 9 | 31.908 6 | 31.900 8 | 31.927 9 |
| 4 | 31.914 7 | 31.922 7 | 32.898 3 | 31.914 6 |
| 5 | 31.907 9 | 31.954 4 | 31.897 4 | 31.926 0 |
| 6 | 31.830 7 | 31.918 1 | 32.899 8 | 31.943 0 |
| 7 | 31.923 8 | 32.032 0 | 31.897 7 | 31.915 0 |
| 8 | 31.977 3 | 31.977 6 | 32.896 8 | 31.926 2 |
| 9 | 31.906 9 | 31.905 4 | 32.897 6 | 31.930 7 |
| 10 | 31.860 0 | 32.040 0 | 31.900 0 | 31.920 0 |
| Mean | 31.895 2 | 31.947 3 | 32.398 0 | 31.940 8 |
| Algorithm | Kp | Ki | Kd | J1 | Mp | tr | ts | ess |
| PSO_PID | 7.765 8 | 4.249 50 | 0.736 7 | 32.899 8 | 2.033 0 | 2.500 0 | 23.300 0 | 0.996 1 |
| BCS_PID | 7.825 0 | 4.316 20 | 0.717 2 | 31.918 1 | 2.037 0 | 2.500 0 | 23.100 0 | 0.997 3 |
| ICS_PID | 7.908 5 | 4.242 13 | 0.690 2 | 31.943 0 | 2.039 0 | 2.400 0 | 23.000 0 | 0.999 5 |
| Proposed CS_PID | 7.846 7 | 4.351 40 | 0.718 9 | 31.830 7 | 2.033 0 | 2.400 0 | 16.900 0 | 1.000 1 |
考虑一个二阶加时滞不稳定对象[22]:
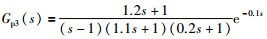
|
(23) |
其中,时滞时间τ为0.1.
在PID控制器的设计中,控制系统的一般约束为对象的产出和控制器的输出.根据系统的特定需求,这个例子的约束可以表示为
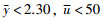
|
(24) |
这样,综合目标函数可以描述为
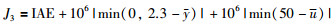
|
(25) |
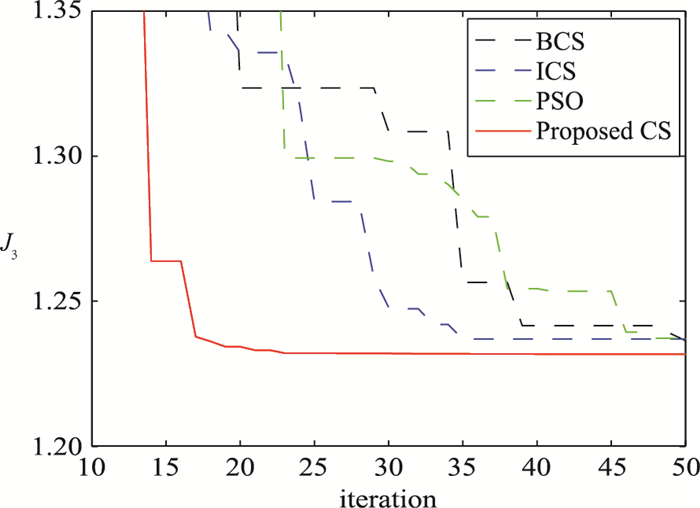
图 6给出了在PSO,CS,ICS以及改进的CS这4个不同智能优化算法下综合性能目标J3的收敛特性. 表 6展示了在不同算法不同次试验下的综合目标J3值. 表 7给出了在随机一次试验中,不同优化算法下整定得到的参数以及系统的最大超调量Mp、上升时间tr、调整时间ts、稳态误差ess.在这个例子中,通过图 6和表 6、表 7的比较,使用所提出的算法,估计的PID参数能够获得最佳的控制性能.
| Method | Proposed CS | CS | PSO | ICS |
| 1 | 1.231 7 | 1.234 3 | 1.237 2 | 1.235 1 |
| 2 | 1.231 7 | 1.232 1 | 1.235 7 | 1.236 0 |
| 3 | 1.231 6 | 1.236 3 | 1.237 2 | 1.236 9 |
| 4 | 1.231 7 | 1.234 7 | 1.239 8 | 1.232 1 |
| 5 | 1.231 6 | 1.236 9 | 1.235 3 | 1.237 1 |
| 6 | 1.231 7 | 1.234 6 | 1.236 5 | 1.232 7 |
| 7 | 1.231 7 | 1.239 9 | 1.235 7 | 1.234 4 |
| 8 | 1.231 6 | 1.234 5 | 1.242 5 | 1.232 9 |
| 9 | 1.231 7 | 1.234 8 | 1.242 3 | 1.233 8 |
| 10 | 1.231 7 | 1.244 2 | 1.242 2 | 1.234 7 |
| Mean | 1.231 7 | 1.236 2 | 1.238 4 | 1.234 6 |
| Algorithm | Kp | Ki | Kd | J1 | Mp | tr | ts | ess |
| PSO_PID | 3.309 2 | 1.250 2 | 0.298 8 | 1.235 4 | 2.265 0 | 1.500 0 | 5.300 0 | 1.000 0 |
| BCS_PID | 3.290 8 | 1.229 7 | 0.300 6 | 1.234 6 | 2.264 0 | 1.500 0 | 5.300 0 | 1.000 0 |
| ICS_PID | 3.288 4 | 1.187 3 | 0.307 4 | 1.235 3 | 2.262 0 | 1.500 0 | 5.400 0 | 1.000 0 |
| Proposed CS_PID | 3.336 6 | 1.146 9 | 0.310 2 | 1.231 7 | 2.261 0 | 1.500 0 | 5.30 00 | 1.000 0 |
|
| 图 6 例3中基于不同PID整定方法下的收敛性能曲线 Figure 6 The convergence curves by using different PID tuning methods in Example 3 |
本文提出一种新的改进的布谷鸟搜索算法来处理多目标不稳定时滞系统的PID控制器整定问题.通过结合标准的布谷鸟搜索算法和局部搜索能力强的NLJ算法,该算法取得了较好的鲁棒性和全局优化的准确性.此外,文中还使用了t分布序列来优化算法的初始种群.通过与传统PSO算法、基本CS算法和ICS算法[22]相比,实验仿真结果验证了该方法的有效性.最后,文中提出的改进布谷鸟搜索算法可以扩展到以下情况:
1) 多输入多输出(MIMO)时滞系统的PID控制器参数优化;
2) 模块化非线性系统辨识,如:MIMO-Hammerstein模型辨识和MIMO-wiener模型辨识.
| [1] | Nikita S, Chidambaram M. Tuning of PID controllers for time delay unstable systems with two unstable poles[J]. IFAC Papersonline, 2016, 49(1): 801–806. DOI:10.1016/j.ifacol.2016.03.155 |
| [2] | Jin Q B, Liu Q. IMC-PID design based on model matching approach and closed-loop shaping[J]. ISA Transactions, 2014, 53(2): 462. DOI:10.1016/j.isatra.2013.11.005 |
| [3] | Wang Z, Su Q, Luo X. A novel HTD-CS based PID controller tuning method for time delay continuous systems with multi-objective and multi-constraint optimization[J]. Chemical Engineering Research & Design, 2016, 115: 98–106. |
| [4] |
马增辉, 刘长良.
一类非最小相位系统的PID控制器整定方法[J]. 信息与控制, 2015, 44(2): 147–151.
Ma Z H, Liu C L. Tuning method for a PID controller in a non-minimum phase system[J]. Information and Control, 2015, 44(2): 147–151. |
| [5] | Aström K J, Hägglund T. Revisiting the Ziegler-Nichols step response method for PID control[J]. Journal of Process Control, 2004, 14(6): 635–650. DOI:10.1016/j.jprocont.2004.01.002 |
| [6] | Bahavarnia M S, Tavazoei M S. A new view to Ziegler-Nichols step response tuning method:Analytic non-fragility justification[J]. Journal of Process Control, 2013, 23(1): 23–33. DOI:10.1016/j.jprocont.2012.10.012 |
| [7] | Wang Y J, Shang-Hong S, Chi-Kuang L, et al. Determination of all feasible robust PID Controllers for open-loop unstable plus time delay systems with gain margin and phase margin specifications[C]//Proceedings of the IEEE Control Conference. Piscataway, NJ, USA: IEEE, 2011: 2394-2399. |
| [8] | Jin Q B, Liu Q, Huang B. New results on the robust stability of PID controllers with gain and phase margins for UFOPTD processes[J]. ISA Transactions, 2016, 61: 240–250. DOI:10.1016/j.isatra.2015.11.028 |
| [9] |
杨智, 陈志堂, 范正平, 等.
基于改进粒子群优化算法的PID控制器整定[J]. 控制理论与应用, 2010, 27(10): 1345–1352.
Yang Z, Chen Z T, Fan Z P, et al. Tuning of PID controller based on improved particle-swarm-optimization[J]. Control Theory and Applications, 2010, 27(10): 1345–1352. |
| [10] | Jin Q B, Hao F, Wang Q. A multivariable IMC-PID method for non-square large time delay systems using NPSO algorithm[J]. Journal of Process Control, 2013, 23(5): 649–663. DOI:10.1016/j.jprocont.2013.02.007 |
| [11] |
唐贤伦, 张衡, 周家林, 等.
基于多Agent混沌粒子群优化的磁悬浮系统PID控制器[J]. 信息与控制, 2013, 42(6): 758–764.
Tang X L, Zhang H, Zhou J L, et al. PID controller of magnetic suspension system based on CPSO in multi-agent architecture[J]. Information and Control, 2013, 42(6): 758–764. |
| [12] | Yang X S, Deb S. Cuckoo search via Lévy flights[C]//Proceedings of World Congress on Nature & Biologically Inspired Computing. Piscataway, NJ, USA: IEEE, 2009: 210-214. |
| [13] |
董崇杰, 刘毅, 彭勇.
改进布谷鸟算法在人群疏散多目标优化中的应用[J]. 系统仿真学报, 2016, 28(5): 1063–1069.
Dong C J, Liu Y, Peng Y. Improved cuckoo search algorithm applied to multi-objective optimization of crowd evacuation[J]. System Simulation, 2016, 28(5): 1063–1069. |
| [14] | Teymourian E, Kayvanfar V, Komaki G M, et al. Enhanced intelligent water drops and cuckoo search algorithms for solving the capacitated vehicle routing problem[J]. Information Sciences, 2016, s334-335(1): 354–378. |
| [15] |
明波, 黄强, 王义民, 等.
基于改进布谷鸟算法的梯级水库优化调度研究[J]. 水利学报, 2015, 46(3): 341–349.
Ming B, Huang Q, Wang Y M, et al. Research on optimal operation of cascade reservoirs based on improved cuckoo algorithm[J]. Journal of Hydraulic Engineering, 2015, 46(3): 341–349. |
| [16] | Huang L, Ding S, Yu S, et al. Chaos-enhanced cuckoo search optimization algorithms for global optimization[J]. Applied Mathematical Modelling, 2015, 40(5/6): 3860–3875. |
| [17] | Jia B, Yu B, Wu Q, et al. Adaptive affinity propagation method based on improved cuckoo search[J]. Knowledge-Based Systems, 2017, 111: 27–35. |
| [18] | Wakaiki M, Yamamoto Y, Özbay H. Stable controllers for robust stabilization of systems with infinitely many unstable poles[J]. Systems & Control Letters, 2013, 62(62): 511–516. |
| [19] | Li T, Georgakis C. Dynamic input signal design for the identification of constrained systems[J]. Journal of Process Control, 2008, 18(3/4): 332–346. |
| [20] | Begum K G, Rao A S, Radhakrishnan T K. Maximum sensitivity based analytical tuning rules for PID controllers for unstable dead time processes[J]. Chemical Engineering Research & Design, 2016, 109: 593–606. |
| [21] | Nikita S, Chidambaram M. Tuning of PID controllers for time delay unstable systems with two unstable poles[J]. IFAC Papersonline, 2016, 49(1): 801–806. DOI:10.1016/j.ifacol.2016.03.155 |
| [22] | Lee S C, Wang Q G. Stabilization conditions for a class of unstable delay processes of higher order[J]. Journal of the Taiwan Institute of Chemical Engineers, 2010, 41(4): 440–445. DOI:10.1016/j.jtice.2010.03.001 |



