0 引言
近年来,多智能体网络一致性的发展日新月异,其广泛应用于同步运动、群集运动、城市交通控制等方面.一致性问题俨然成为学者们关注的热点之一,并取得了不计其数的成果[1-6].
目前,大多数文献主要针对的是多智能体网络的完全一致性,如文[7-12].随着时代的飞速发展,系统规模、通信技术正日益提升,智能体之间存在性能和合作任务上的差异,智能体的关键信息收敛到单一点往往不太适用[13],它们被分成了多个群体,同一群体内的关键信息收敛到一致,不同群体内的一致性状态可以不同.显然,研究群的一致性更加适用于处理复杂多样的一致性问题.完全一致性可以看作是群一致性的特例.近年来,群一致性问题的研究取得了一定的进展,如文[14]分析了1阶多智能体网络在无向固定拓扑结构下的群一致性问题,并给出了判断群一致性收敛的若干条准则;文[15]针对系统有延迟的情况下,分别研究了1阶多智能体系统在固定拓扑和切换拓扑下的群一致性;文[16]在切换拓扑网络下,考虑了信息交流存在的时滞,基于双树形变化设计控制协议,分析了1阶多智能体网络的群一致性问题.随着研究的深入,文[17]基于所有子群满足入度平衡的前提下,讨论了2阶多智能体网络在固定拓扑结构下的群的一致性问题;文[18]提出了基于连通二部图特性的控制协议,实现了2阶多智能体系统的群一致性.另一方面,由于实际网络节点的规模较大,通信资源有限,因此只针对部分节点进行控制比较经济高效,更具有实际意义[19].牵引控制方法即只牵引网络中的部分节点,从而达到控制整个网络的目的,文[20]讨论了多智能体系统在牵引控制下的群一致性问题.
然而,在上述群一致性的研究成果中,大多数是假定通信拓扑结构为固定的,例如文[14, 17, 20].考虑到通信范围的有限,网络节点间的连接会受到环境的影响,邻居节点之间的连接时通时断,这就使得研究固定拓扑下的群一致性较为局限.虽然文[16, 18]是在切换网络下研究多智能体系统的群一致性,但是均以1阶系统模型为研究对象.实际系统中,比如无人机、机器人等系统的加速度比速度、位置更易控制,因此2阶多智能体系统更具实际意义.另外,多智能体网络在时变牵引控制下的群一致性研究还未引起广泛关注,比如文[20]考虑了牵引控制的群一致性问题,但牵引控制是固定的.
基于上述讨论,本文进一步研究了2阶多智能体网络的群一致性问题,主要创新点在于考虑了网络结构具有拓扑切换的情形,同时控制协议中引入了时变的牵引控制.基于代数图论、线性矩阵不等式和李亚普诺夫稳定性理论,推导出了群一致性的充分条件.
定义符号:R表示实数集,Rn×n表示n×n阶实矩阵集合,Λ(H)表示矩阵H所有特征根的集合,Re(·)表示特征根的实部,Im(·)表示特征根的虚部,·表示向量的欧几里得范数,矩阵P>0表示矩阵P是正定的.
1 问题描述 1.1 预备知识首先给出本文所需的图论知识[21].
用G=(W,E,A)表示具有n+m个节点的有向图,其中网络节点集为W={w1,w2,…,wn+m},节点的下标集表示为I={1,2,…,n+m},边集为E⊆W×W.节点wi的邻居集为Ni={wj|wj∈W:(wi,wj)∈E}.图G的邻接矩阵为A=[aij](n+m)×(n+m),如果存在节点wj到节点wi的信息流,则aij≠0,对于任意的节点wi∈W,定义aii=0. L=[lij](n+m)×(n+m)为图G的拉普拉斯矩阵且lij= 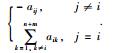
若图G含有一条有向路径,则存在一系列有序连通边集(wi,wi1),(wi1,wi2),…,(wil,wj),其中(wik,wik+1)∈E,k=1,2,…,l.假设节点wi在图G中存在到达其余节点的路径,则称节点wi全局可达.
本文考虑将图G分为两个子群的情形,即G1和G2,若G1=(W1,E1,A1)是图G=(W,E,A)的子图,则存在W1⊂W,E1⊂E.对于任意节点wi,定义在G1中的节点集为W1={w1,w2,…,wn},下标集I1={1,2,…,n},其中邻居集N1i={wj∈W1:(wj,wi)∈E}.同理,在子群G2中,节点集为W2={wn+1,wn+2,…,wn+m},I2={n+1,n+2,…,n+m},N2i={wj∈W2:(wj,wi)∈E}.显然,可以得到Ni=N1i∪N2i.
假设1 图G邻接矩阵A的元素满足:
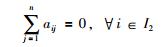
|
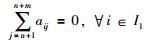
|
注1 从假设1可以看出,邻接系数aij可以取负值,即对于任意智能体wi,与其不同子群的邻居可以存在负权值边,反映两者之间的竞争关系,符合实际网络情形.
1.2 模型描述本文研究的2阶多智能体网络是由n+m个智能体组成,每个智能体的动态方程为
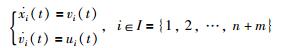
|
(1) |
其中,为了简单起见,考虑xi(t)∈R,vi(t)∈R,ui(t)∈R,分别表示第i个智能体在t时刻的位置、速度与控制输入.
本文考虑了两个子群的情形,其中虚拟领导者l1和l2分别属于G1和G2,针对每个子群,令虚拟领导者:
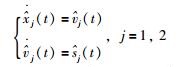
|
(2) |
其中,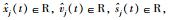
定义1 对于任意初始条件xi(0)∈R,vi(0)∈R(i∈I={1,2,…,n+m}),如果满足条件:
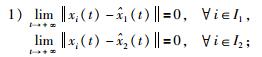
|
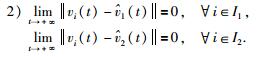
|
则称2阶多智能体网络(1)实现群一致性.
2 主要结果 2.1 控制策略基于牵引控制策略,结合多智能体网络(1)和(2)的模型,本文给出控制协议ui(t),即:
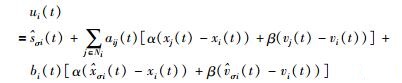
|
(3) |
其中,控制参数α>0,β>0.当i∈I1时,σi=1,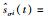
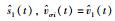
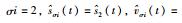
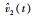
注2 本文中,邻接系数aij(t)是可以随时间变化的,反映的是智能体之间的连接边随时间发生的变化,即网络拓扑为切换情形.
针对2阶多智能网络(1),考虑实际环境的影响,智能体之间的通信链路经常发生断裂,因此智能体的拓扑结构可能会随时切换.本文引入切换拓扑信号g(t):[0,+∞)→Γ={1,2,…,q},q>1.切换拓扑结构图记为Gg(t),对应的拉普拉斯矩阵为Lg(t).对于任意t≥0,定义该系统切换的时间序列为t0 < t1 < t2 < … < tk < tk+1 < …,其中t0=0,k=0,1,2,….在每个切换时间段[tk,tk+1)上,领导者的牵引控制可以随时间变化,即bi(t)可以发生有限次的变化.进一步地,假设[tk,tk+1)可以分为tk=tk(1) < tk(2) < … < tk(nk)=tk+1,其中nk∈N且nk>2,令:
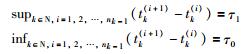
|
在每段上bi(t)是固定不变的.
为了便于理论分析,此处引入2个假设条件:
假设2 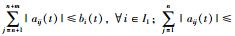
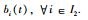
假设3 2阶多智能体网络(1)中的拉普拉斯矩阵L(t)满足有且只有2个零特征值,并且其它特征值均具有正实部.
注3 不失一般性,假设[tk(1),tk(2))上网络拓扑及牵引控制bi(t)满足假设2和假设3,即只需一段时间上满足即可;将满足假设2与假设3下的L(t)记为L1(t).
令2阶多智能体网络(1)的位置测量误差、速度测量误差分别为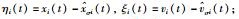
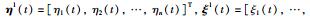
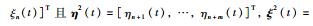
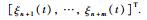
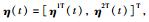
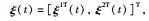
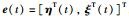
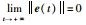
由式(1)~式(3)可知:
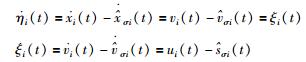
|
可以推出:
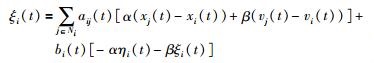
|
(4) |
由拉普拉斯矩阵的定义及假设1,式(4)可以变为
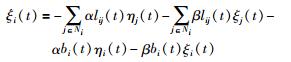
|
(5) |
为了便于计算,引入矩阵H(t)=L(t)+B(t),其中B(t)=diag{b1(t),…,bn+m(t)}代表来自虚拟领导者边的权重且bi(t)≥0.
令 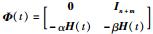
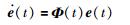
|
(6) |
引理1[16] 若L(t)满足假设1~假设3,并且存在任何一个具有外部作用的节点在图G中全局可达且可以接收领导者的信息(即bi(t)>0),则矩阵H是正稳定的(矩阵H所有特征根的实部均为正实数).
注4 对于智能体wi,如果存在来自不同子群内智能体wj的连接边,那么称此节点wi为具有外部作用的节点.
引理2[16] 如果矩阵Φ(t)是赫尔维茨稳定的,即Reλi,± < 0,当且仅当H是正稳定的,则有不等式(7)成立:
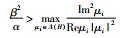
|
(7) |
本节将给出多智能体网络(1)的群一致性充分条件.假设在每个切换段[tk(1),tk(2))上,存在一个相同的Φ1= 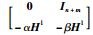
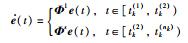
|
(8) |
其中s≥1,k∈N.
在给出主要定理之前,先通过算法1寻求定理所需要的参数:
算法1 为了实现2阶多智能体网络(1)的群一致性,通过线性矩阵不等式确定正定矩阵P、参数δ和参数γ:
1) 寻找正定矩阵P>0,使得Φ1TP+PΦ1 < 0;
2) 寻找δ>0,使得Φ1TP+PΦ1+δP < 0;
3) 对于其余切换拓扑及牵引控制下的Φs,寻找γ,使ΦsTP+PΦs < γP.
注5 本文考虑网络拓扑是切换的,在算法1中,需要知道拓扑结构对应的矩阵Φ1及Φs(s≥1),这具有一定的局限性.如何拓广到更一般情形,也是本文下一步研究的方向.
定理1 考虑2阶多智能体网络(1)的邻接系数满足假设1,并且在任意切换区间[tk,tk+1)中,时间段[tk(1),tk(2))上智能体网络满足假设2与假设3;进一步地,网络中任何一个具有外部作用的节点在图G中全局可达,控制协议(3)中的参数α、β满足式(7);若存在常数l>0,使得δ(tk(2)-tk)-γ(tk+1-tk(2))>l(其中δ、γ同算法1),则2阶多智能体网络(1)实现群一致性.
证明 对于任意t∈[tk,tk+1),构建李亚普诺夫函数:
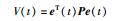
|
(9) |
这里的矩阵P即为算法1中的矩阵P.
对于任意的t∈[tk(1),tk(2)),k∈N,考虑式(9)沿着系统(8)的轨迹的导数,根据算法1中的步骤2)可知:
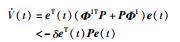
|
(10) |
同理,对于t∈[tk(2),tk(nk)),k∈N,根据算法1中步骤3)可知:
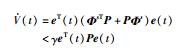
|
(11) |
结合式(10)和式(11)可得:
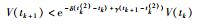
|
(12) |
因为对于任意的k∈N,都有δ(tk(2)-tk)-γ(tk+1-tk(2))>l成立,故式(12)满足V(tk+1) < e-lV(tk),其中l>0,可见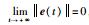
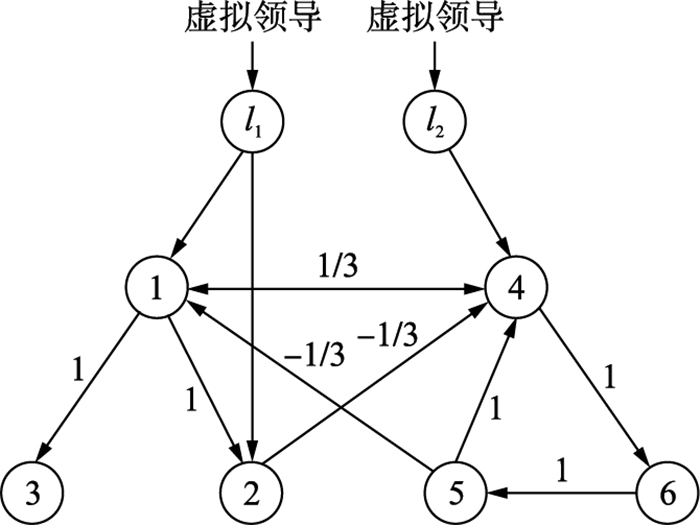
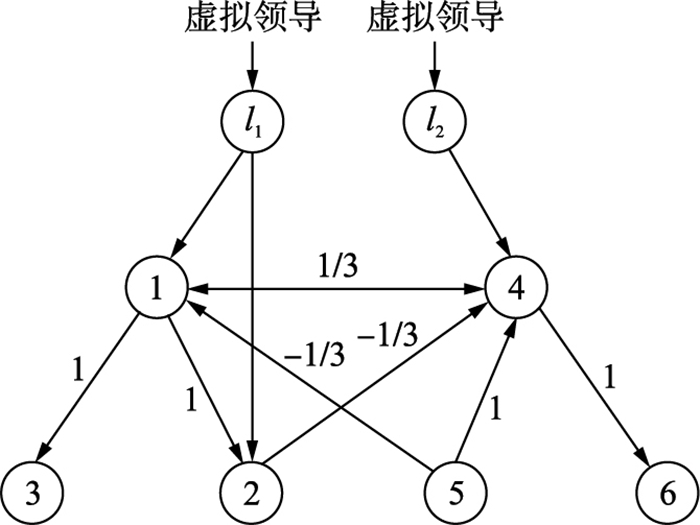
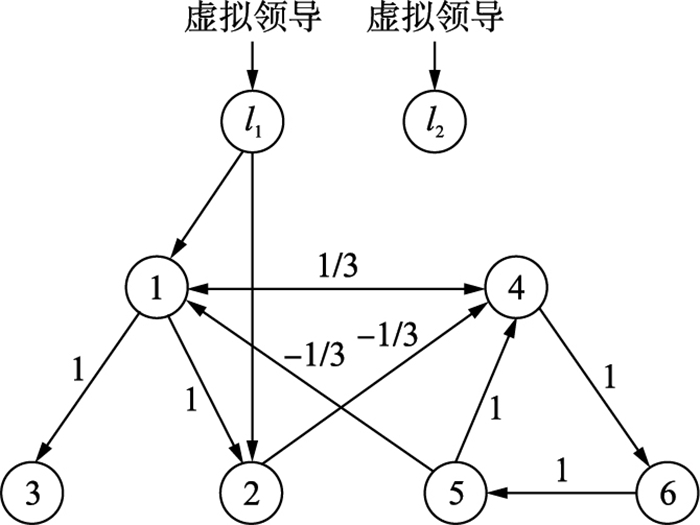
本节给出具体仿真例子来验证以上分析的结果.假设2阶多智能体网络由8个智能体构成,包括2个虚拟领导者,6个跟随者.其中,跟随者{1,2,3}属于G1,{4,5,6}属于G2,智能体1和智能体4为具有外部作用的节点.为简单起见,假设任意时间段[tk,tk+1)的网络及时变牵引在{G1,G2,G3}中切换,如图 1~图 3所示.
|
| 图 1 切换拓扑图G1 Fig.1 Switching topology G1 |
|
| 图 2 切换拓扑图G2 Fig.2 Switching topology G2 |
|
| 图 3 切换拓扑图G3 Fig.3 Switching topology G3 |
选取跟随者的初始位置为x(0)=[0.1,0.3,0.5,0.7,0.9,1.1]T,初始速度v(0)=[0.2,0.4,0.6,0.8,1.0,1.2]T,虚拟领导者的初始位置为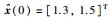
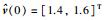
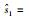
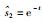
以图 1为例,图G1对应的拉普拉斯矩阵L1= 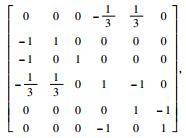
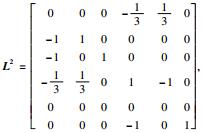
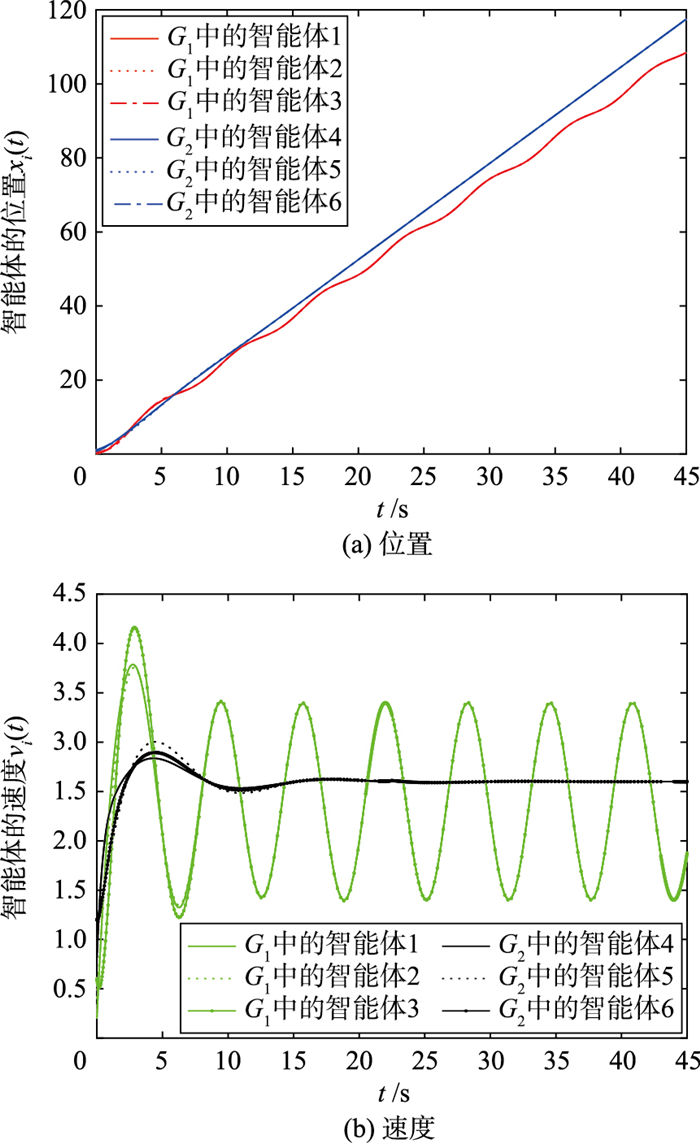
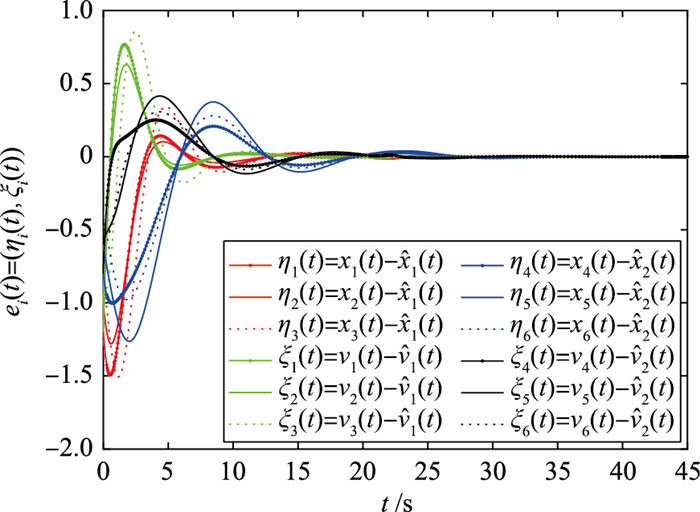
1) 选取控制参数α=1,β=1.5,通过算法1求出定理1所需的参数δ=0.159 6,γ=3.233 1,切换的时间区间比值为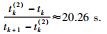
|
| 图 4 智能体轨迹图 Fig.4 The trajectories of the agents |
|
| 图 5 α=1,β=1.5误差系统ei(t)(i=1,2,…,6)的演化图 Fig.5 Evolution of errors ei(t) with α=1, β=1.5(i=1, 2, …, 6) |
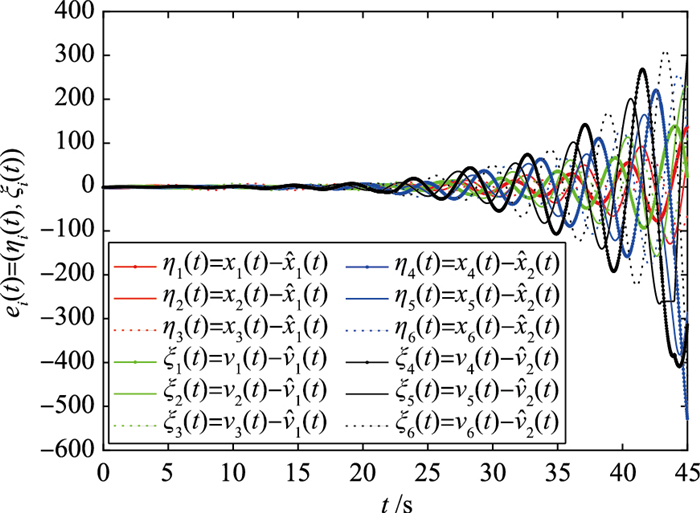
2) 若选取控制参数α=1,β=0.1,可以看出β的选取不符合定理1中的条件,所以多智能体网络在一致性协议(3)中不能实现群一致性.如图 6所示,最终的误差系统不满足
|
| 图 6 α=1,β=0.1误差系统ei(t)(i=1,2,…,6)的演化图 Fig.6 Evolution of errors ei(t) with α=1, β=0.1(i=1, 2, …, 6) |
本文研究了2阶多智能体网络在切换拓扑结构下的群一致性问题.通过虚拟领导者对部分跟随者的时变牵引控制,实现了所有跟随者趋于两组一致.给出了群一致性所需要的充分条件,依赖于网络拓扑结构与牵引控制及控制协议中的相关参数.进一步地,利用李亚普诺夫稳定性理论证明了该条件的正确性;所提供的Matlab仿真验证了定理的有效性.值得注意的是,本文所给出的结果基于拓扑切换所对应的矩阵Φ为已知情形,在今后的工作中,将进一步研究如何推广到更一般(未知或部分未知)情形,同时也将着力于离散、非线性系统的群一致性.
| [1] | Wang P K C, Hadaegh F Y. Coordination and control of multiple microspacecraft moving information[J]. Journal of the Astronautical Sciences, 1996, 44(3): 315–355. |
| [2] | Chen Y, Lu J H, Yu X H, et al. Multi-agent systems with dynamical topologies:Consensus and applications[J]. IEEE Circuits and Systems Magazine, 2013, 13(3): 21–34. DOI:10.1109/MCAS.2013.2271443 |
| [3] |
欧海涛, 张文渊, 张卫东, 等.
城市交通控制研究的新发展[J]. 信息与控制, 2000, 29(5): 441–453.
Ou H T, Zhang W Y, Zhang W D, et al. New trend toward urban traffic control[J]. Information and Control, 2000, 29(5): 441–453. DOI:10.3969/j.issn.1002-0411.2000.05.010 |
| [4] |
曹美会, 鲜斌, 张旭, 等.
基于视觉的四旋翼无人机自主定位与控制系统[J]. 信息与控制, 2015, 44(2): 190–196, 202.
Cao M H, Xian B, Zhang X, et al. An autonomous vision-based localization and control system for quadrotor UAV[J]. Information and Control, 2015, 44(2): 190–196, 202. |
| [5] | Ren W, Atkins E. Distributed multi-vehicle coordinated control via local information exchange[J]. International Journal of Robust and Nonlinear Control, 2007, 17(10/11): 1002–1033. |
| [6] | Andrea B, Albert D. Consensus in networks of mobile communicating agents[J]. Physical Review E, 2012, 85(1): 016113. DOI:10.1103/PhysRevE.85.016113 |
| [7] | Nian X H, Su S J, Pan H. Consensus tracking protocol and formation control of multiagent systems with switching topology[J]. Journal of Central South University of Technology, 2011, 18(4): 1178–1183. DOI:10.1007/s11771-011-0820-5 |
| [8] | Guan Y Q, Wang L. Structural controllability of multi-agent systems with absolute protocol under fixed and switching topologies[J]. Science China-Information Sciences, 2017, 60(9): 226–240. |
| [9] | Yu W W, Chen G R, Cao M. Some necessary and sufficient conditions for second-order consensus in multi-agent dynamical systems[J]. Automatica, 2010, 46(6): 1089–1095. DOI:10.1016/j.automatica.2010.03.006 |
| [10] |
纪良浩, 廖晓峰.
具有不同时延的多智能体系统一致性分析[J]. 物理学报, 2012, 61(15): 8–16.
Ji L H, Liao X F. Consensus analysis of mobile multi-agent system with multiple time delays[J]. Acta Physica Sinica, 2012, 61(15): 8–16. |
| [11] | Wen G H, Duan Z S, Yu W W, et al. Consensus of second-order multi-agent systems with delayed nonlinear dynamics and intermittent communications[J]. International Journal of Control, 2013, 86(2): 322–331. DOI:10.1080/00207179.2012.727473 |
| [12] | Dimarogonas D V, Frazzoli E, Johansson K H. Distributed event-triggered control for multi-agent systems[J]. IEEE Transactions on Automatic Control, 2012, 57(5): 1291–1297. DOI:10.1109/TAC.2011.2174666 |
| [13] | Wang Q, Wang Y Z. Cluster synchronization of a class of multi-agent systems with a bipartite graph topology[J]. Science China-Information Sciences, 2014, 57(1): 012203. |
| [14] | Yu J Y, Wang L. Group consensus of multi-agent systems with undirected communication graphs[C]//7th Asian Control Conference. Piscataway, NJ, USA: IEEE, 2009: 105-110. |
| [15] | Xia H, Huang T Z, Shao J L, et al. Group consensus of multi-agent systems with communication delays[J]. Neurocomputing, 2016, 171(C): 1666–1673. |
| [16] | Yu J Y, Wang L. Group consensus of multi-agent systems with undirected communication exchange[J]. International Journal of Systems Science, 2012, 43(2): 334–348. DOI:10.1080/00207721.2010.496056 |
| [17] | Cui Q, Xie D M, Jiang F C. Group consensus tracking control of second-order multi-agent systems with directed fixed topology[J]. Neurocomputing, 2016, 218(7): 286–295. |
| [18] |
林瑜阳, 李钟慎.
基于连通二部图的二阶多智能体系统分组一致性分析[J]. 信息与控制, 2017, 46(1): 7–12.
Lin Y Y, Li Z S. Group consensus analysis on second-order multi-agent systems based on the connected bipartite graph[J]. Information and Control, 2017, 46(1): 7–12. |
| [19] | Wu C W. Localization of effective pinning control in complex networks of dynamical systems[C]//2008 IEEE International Symposium Circuits and Systems. Piscataway, NJ, USA: IEEE, 2008: 2530-2533. |
| [20] | Wang T, Li T, Yang X, et al. Cluster synchronization for delayed Lur'e dynamical networks based on pinning control[J]. Neurocomputing, 2012, 83(15): 72–82. |
| [21] |
戴一奇, 胡冠章, 陈卫.
图论与代数结构[M]. 北京: 清华大学出版社, 1995: 1-35.
Dai Y Q, Hu G Z, Chen W. Graph theory and algebraic structure[M]. Beijing: Tsinghua University Press, 1995: 1-35. |



