2. 辽宁大学轻型产业学院, 辽宁 沈阳 110036;
3. 沈阳理工大学, 辽宁 沈阳 110159
2. College of Light Industry, Liaoning University, Shenyang 110036, China;
3. Shenyang Ligong University, Shenyang 110159, China
0 引言
由于分数阶算子具有记忆性,与整数阶系统相比,分数阶系统模型能够更好地揭示实际物理系统的动态特性[1].同时,将分数阶微积分的概念引入到控制器设计中,可以使控制器设计变得更加灵活,闭环控制系统可以获得更好的控制效果,因此分数阶系统的建模与控制问题近些年来引起了很多学者的广泛关注[2].随着分数阶微积分在控制系统理论中的广泛应用,已有的研究证明,分数阶动态系统模型是描述具有记忆性、粘弹性、扩散性的动力学系统的有力工具[3].
考虑到分数阶系统分析和控制器设计需要系统的状态信息,因此有必要对系统进行状态估计.实际系统输入和输出的采样信号经常受一些外界噪声的干扰,因此需要设计滤波器来获得有效的系统状态信息[4].针对整数阶系统的状态估计问题,很多学者已给出许多滤波方法,如卡尔曼滤波、扩展卡尔曼滤波和H∞滤波等方法.扩展卡尔曼滤波(extended Kalman filter)[5-6]和无迹卡尔曼滤波器(unscented Kalman filter)[7-8]是两种最常用的非线性系统状态估计方法.文[6]提出了一种解决含有未知输入的离散时间非线性系统状态和故障估计的自适应扩展卡尔曼滤波器设计方法.文[9]利用反馈控制的协方差自适应方法,提出了一种线性时不变系统自适应卡尔曼滤波器.文[10]和文[11]分别讨论了电动汽车的电池荷电状态和假手系统模型的自适应卡尔曼滤波器设计方法.
随着分数阶动态模型的引入,通常使用分数阶卡尔曼滤波器来实现系统的状态估计和参数估计问题.文[12]针对离散时间的线性和非线性分数阶系统提出了分数阶卡尔曼滤波器和分数阶扩展卡尔曼滤波器,并将这些算法用于分数阶系统中未知参数的估计.文[13]研究了含有未知参数的时滞不确定分数阶复杂网络系统的参数估计问题.文[14]针对非线性分数阶系统的状态估计问题,研究了一种鲁棒扩展分数阶卡尔曼滤波器.文[15]利用自适应噪声协方差来降低估计误差,并通过模糊逻辑规则改进自适应噪声协方差估计,提出了一种模糊修正的分数阶无迹卡尔曼滤波器来提高状态估计的精度.
近年来,含有非高斯噪声的分数阶系统状态估计问题也日益成为研究的热点,例如Lévy噪声和有色噪声[16-17].因此,为了获得分数阶系统有效的状态估计,文[18-19]通过分解Lévy噪声,实现对Lévy噪声的近似转换,分别提出了针对含有Lévy量测噪声的线性分数阶系统对应的分数阶卡尔曼滤波器和非线性分数阶系统对应的扩展卡尔曼滤波器.文[20]利用分数阶平均导数方法,通过构造有关状态向量和噪声的增广系统,对有色噪声进行处理,提出了含有分数阶有色过程噪声和测量噪声的连续时间线性分数阶系统的分数阶卡尔曼滤波器.文[21]针对测量噪声和过程噪声同时存在的情况,给出了基于分数阶平均导数法和Tustin方法的分数阶卡尔曼滤波器.
分数阶卡尔曼滤波算法通常假定了所需的参数是已知的,然而许多实际系统中的参数不易直接测量,过程噪声和测量噪声也不是理想的高斯白噪声.因此,本文主要研究过程噪声和测量噪声分别为有色噪声且参数未知的情况下连续时间非线性分数阶系统状态和参数估计问题,提出了基于G-L差分方法的自适应分数阶扩展卡尔曼滤波器算法.主要创新点包括:1)利用G-L差分定义的方法将连续时间分数阶系统进行离散化处理,并通过1阶泰勒展开公式将非线性分数阶系统线性化,构造线性差分方程描述系统的动态特征;2)通过两次构造增广向量的方法,处理连续时间非线性分数阶系统中的有色噪声和未知参数问题,实现有效的状态估计;3)讨论历史信息截断问题及其截断选取问题,以便实现算法的工程应用.
1 问题描述分数阶算子主要有Grünwald-Letnikov (G-L)定义、Caputo定义、Riemann-Liouville (R-L)定义三种定义形式.对于函数ξ(t)有:
定义1[1] 函数ξ(t)的α阶G-L导数为
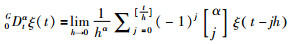
|
(1) |
其中,0GDtα为从0到t时刻的α阶G-L分数阶微分算子,[·]为取整符号,即[r]表示一个小于或等于r的最大整数;
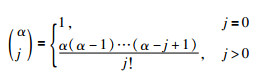
|
定义2[22] 函数ξ(t)的α阶Caputo导数为
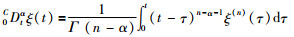
|
(2) |
其中,0CDtα为从0到t时刻的α阶Caputo分数阶微分算子,n-1 < α≤n,α∈R+为分数阶阶次,R+为正实数集,n为正整数,Γ(·)为伽玛函数,满足性质Γ(p+1)=pΓ(p),p∈R+.
在Caputo定义下的分数阶系统初始状态和整数阶系统初始状态的要求是一致的,被广泛地应用于大多数实际物理系统的模型描述中.因此,本文研究Caputo定义下的非线性分数阶系统的卡尔曼滤波器设计问题.
考虑含有未知参数和噪声的连续时间非线性分数阶系统:
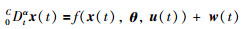
|
(3) |
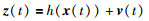
|
(4) |
其中,0CDtα为从0到t时刻的α阶Caputo分数阶微分算子,α∈0,2;f(x(t),θ,u(t))是包含未知参数θ∈Rm的非线性函数;x(t)∈Rn,u(t)∈Rp,z(t)∈Rq分别是状态向量、输入向量和测量向量;w(t)∈Rn,v(t)∈Rq是不相关的过程噪声和测量噪声.
为了叙述方便,采用x(k),u(k),z(k),w(k),v(k)来代替x(t),u(t),z(t),w(t),v(t)在t=kTs点的采样值,其中Ts是采样周期.
当定义1中的间隔h为采样周期Ts时,那么可以获得分数阶G-L差分定义[12],0CDtαx(t)的α阶微分运算近似为
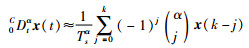
|
(5) |
利用G-L差分离散化方法,有:
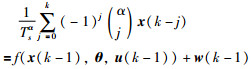
|
(6) |
整理可得
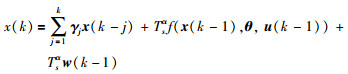
|
(7) |
其中,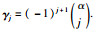
将需要辨识的未知参数向量θ视为满足式(8)的随机变量:
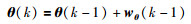
|
(8) |
其中,wθ(k)∈Rr是高斯白噪声,并与w(k)不相关,且E(wθ(k))=0,E(wθ(k)wθT(k))=Q0∈Rr×r.那么,式(7)和式(8)可以表示为增广状态方程:
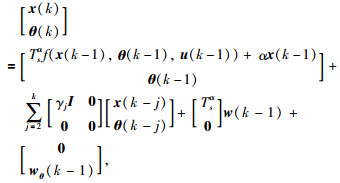
|
(9) |
其中,0为适当维度的零矩阵或零向量,I为适当维数的单位矩阵.
为了简化式(9),定义增广向量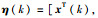
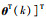
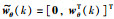
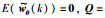
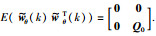
定义矩阵:
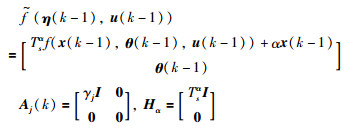
|
则有:

|
(10) |
定义η(k)的估计值和预测值分别为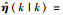
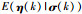
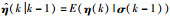
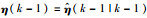
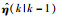
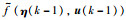
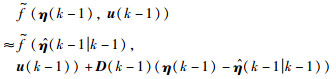
|
(11) |
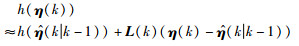
|
(12) |
其中,
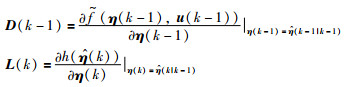
|
将式(11)和(12)代入增广方程(10)中,则有:
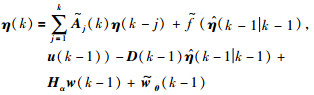
|
(13) |
其中,
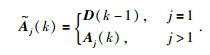
|
通过对方程(11)和方程(12)中非线性函数进行泰勒展开,可以实现非线性函数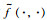
假设测量噪声v(t)的采样值v(k)是高斯白噪声,且E(v(k))=0,E(v(k)vT(l))=Rδ(k-l),过程噪声w(t)是由分数阶方程(14)决定的.
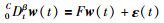
|
(14) |
其中,β∈(0,2);ε(t)的k时刻采样值ε(k)∈Rm是高斯白噪声且E(ε(k))=0,E(ε(k)εT(l))=Nδ(k-l);F∈Rm×m;E(·)是数学期望. δ(k-l)为Kronecker delta函数,即当k≠l时,δ(k-l)=0;当k=l时,δ(k-l)=1.
根据G-L差分定义,式(14)可离散化为
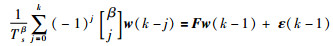
|
(15) |
整理可得
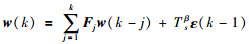
|
(16) |
其中,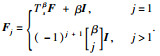
定义增广向量χ(k)=[ηT(k),wT(k)]T和增广噪声向量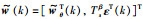
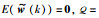
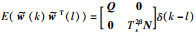
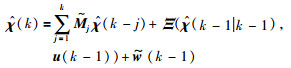
|
(17) |
其中,
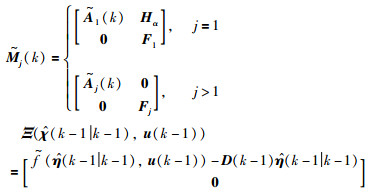
|
因此,输出方程表示为
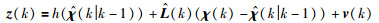
|
其中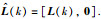
定义χ(k)的估计值和预测值分别为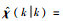
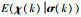
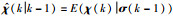
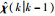
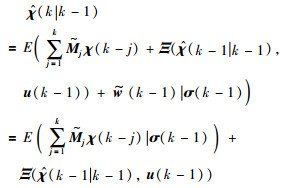
|
(18) |
假设E(χ(k-j)|σ(k-1))=E(χ(k-j)|σ(k-j)),则有:
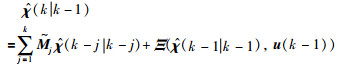
|
(19) |
定理1 针对含有有色过程噪声和未知参数的连续时间非线性分数阶系统,基于G-L差分方法对分数阶系统状态方程(3)和含有有色过程噪声的式(14)离散化,并对离散化后的增广状态方程(17)设计自适应分数阶扩展卡尔曼滤波器来实现系统的状态估计和参数估计,卡尔曼滤波器为
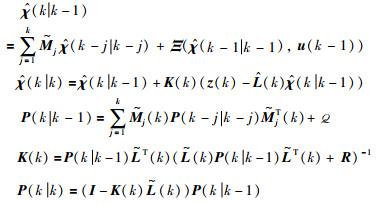
|
证明 根据高斯白噪声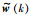
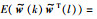
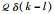
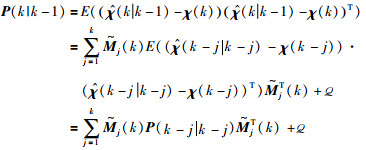
|
χ(k)的估计值的公式定义:
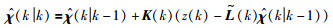
|
(20) |
其中,K(k)为卡尔曼增益矩阵.
由式(20)可得估计误差矩阵:
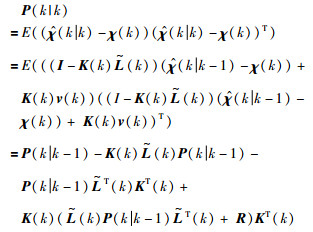
|
(21) |
选取的卡尔曼增益矩阵K(k)使指标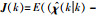
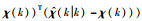
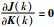
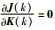
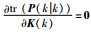
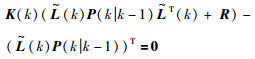
|
(22) |
求解式(22)可得最优滤波增益:
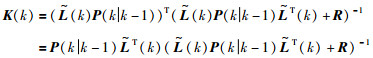
|
将K(k)代入式(21)可得
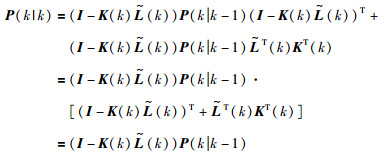
|
注1 为了使定理1描述的分数阶自适应扩展卡尔曼滤波器能够应用于实际的工程中,需要考虑到有限的状态和输入信息存储问题.因此,χ(k)的预测值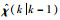
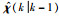
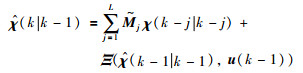
|
(23) |
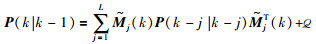
|
(24) |
假设过程噪声w(t)的采样值w(k)是高斯白噪声且E(w(k))=0,E(w(k)wT(l))=Mδ(k-l),测量噪声v(t)是由分数阶方程(25)决定.
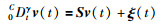
|
(25) |
其中,γ∈(0,2);ξ(t)的k时刻采样值ξ(k)∈Rq是高斯白噪声且E(ξ(k))=0,E(ξ(k)ξT(l))=Nδ(k-l);S∈Rq×q.
根据G-L差分定义,式(25)可离散化为
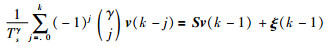
|
(26) |
整理可得
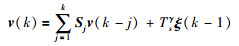
|
(27) |
其中,
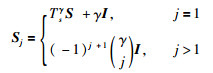
|
定义增广向量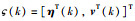
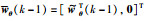
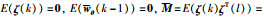
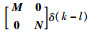
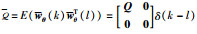
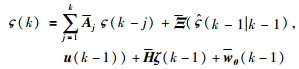
|
(28) |
其中,
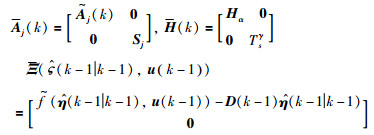
|
因此,输出方程表示为
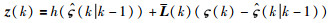
|
(29) |
其中,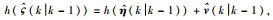
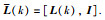
定义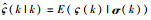
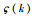
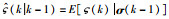
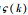
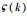
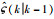
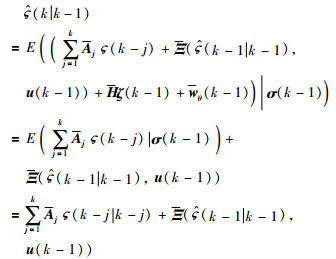
|
(30) |
定理2 针对含有有色测量噪声和未知参数的连续时间非线性分数阶系统,基于G-L差分方法对分数阶系统状态方程(3)和含有有色测量噪声的式(25)离散化,并对离散化后的增广状态方程(28)设计自适应分数阶扩展卡尔曼滤波器来实现系统的状态估计和参数估计,卡尔曼滤波器为
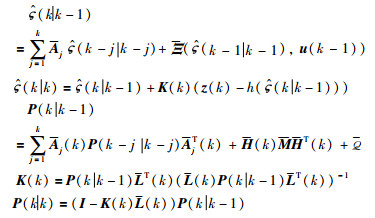
|
证明 根据高斯白噪声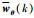
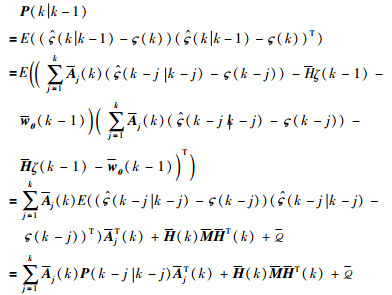
|
此定理中的其它公式的证明与定理1类似,因此详细的证明省略.
注2 为了使定理2设计的分数阶自适应扩展卡尔曼滤波器能够应用于实际的工程中,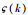
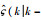
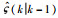
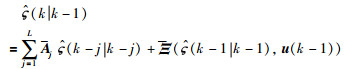
|
(31) |
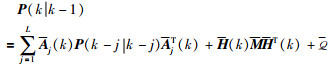
|
(32) |
例1 考虑如下的含有未知参数θ和有色过程噪声w(t)的连续时间非线性分数阶系统:
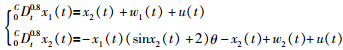
|
(33) |
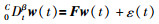
|
(34) |
其中,未知参数、控制输入、状态和过程噪声及其初始值、模型阶次、噪声的协方差矩阵和参数矩阵分别设置为θ=4,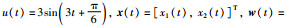
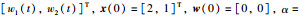
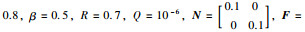
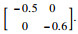
含有测量噪声v(t)的输出方程为z(t)=Hx(t)+v(t),其中H=[1, 1].定理1中的分数阶扩展卡尔曼滤波器的初始条件设置为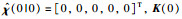
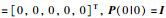
|
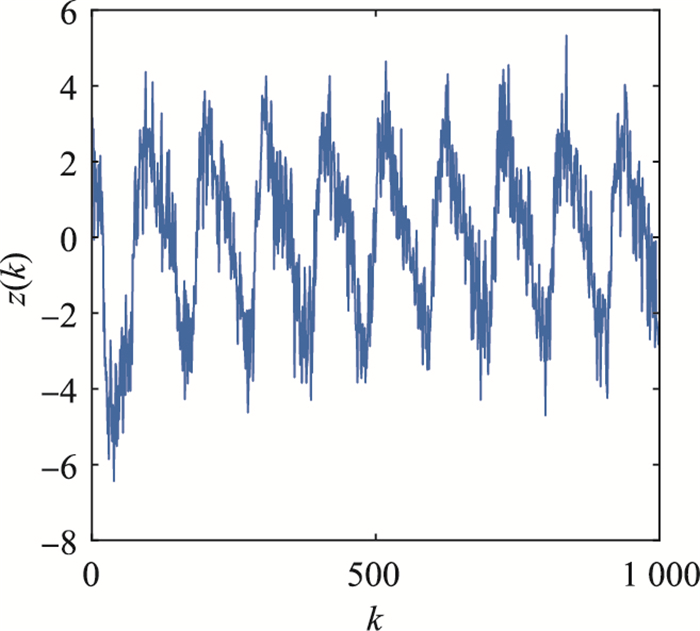
| 图 1 例1中的测量z(k) Fig.1 Measurement z(k) in Example 1 |
为了对不同截断下的估计误差进行比较,定义误差指标:
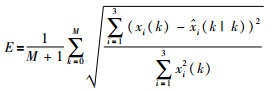
|
(35) |
其中,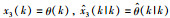
表 1给出了不同截断L时,基于G-L差分定义的自适应扩展卡尔曼滤波器在Ts=0.02 s时,不同未知参数θ的误差估计比较结果.另外,为了讨论随着截断L的增加算法的复杂程度,对不同θ对应的计算时间进行了比较.其中仿真软件为Matlab 2016a,硬件配置为Intel Core i5-5257U,CPU主频和RAM分别为2.70 GHz和4 GB. 表 1的对比结果也验证了对于每个未知参数θ,随着截断L的增大,指标E的值越小,状态估计的精度越高.同样地,从表 1中也可以看出,定理1提出的分数阶自适应扩展卡尔曼滤波器的计算时间随着L的增加而增长.但是运行时间增长幅度明显大于误差增长幅度.因此,有必要选择合适的L值来增加算法的实用性.对于此例中,选取截断L=30是比较合适的.
| L | θ=2 | θ=3 | θ=4 | θ=5 | ||||
| 误差 | 运行时间/s | 误差 | 运行时间/s | 误差 | 运行时间/s | 误差 | 运行时间/s | |
| 10 | 0.274 6 | 0.304 7 | 0.279 0 | 0.284 8 | 0.275 1 | 0.308 8 | 0.226 1 | 0.286 8 |
| 20 | 0.173 4 | 0.467 1 | 0.157 1 | 0.492 1 | 0.160 1 | 0.492 6 | 0.158 4 | 0.476 5 |
| 30 | 0.154 7 | 0.670 7 | 0.145 7 | 0.678 2 | 0.149 8 | 0.669 3 | 0.158 6 | 0.808 4 |
| 40 | 0.138 0 | 0.865 0 | 0.139 4 | 0.907 7 | 0.135 2 | 0.867 7 | 0.139 9 | 1.024 9 |
| 50 | 0.122 1 | 1.068 5 | 0.130 3 | 1.096 8 | 0.125 0 | 1.077 1 | 0.127 1 | 1.058 3 |
| 60 | 0.109 5 | 1.290 4 | 0.120 4 | 1.375 4 | 0.118 1 | 1.263 3 | 0.124 1 | 1.276 7 |
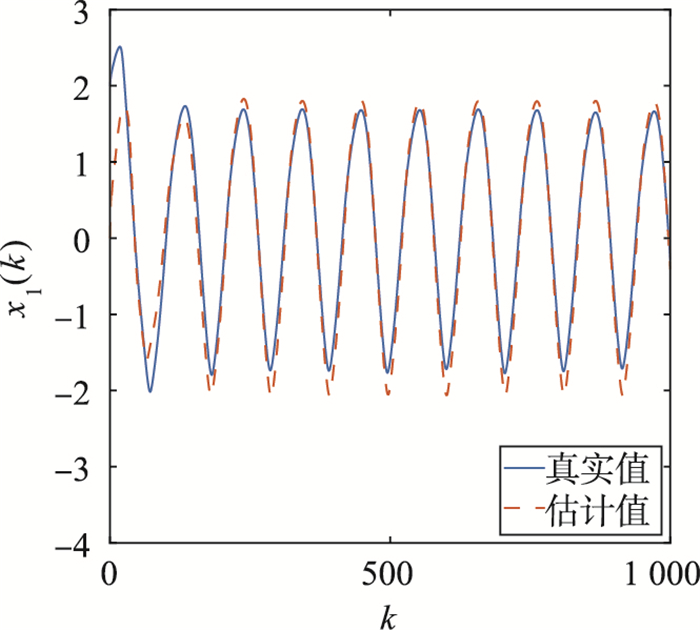
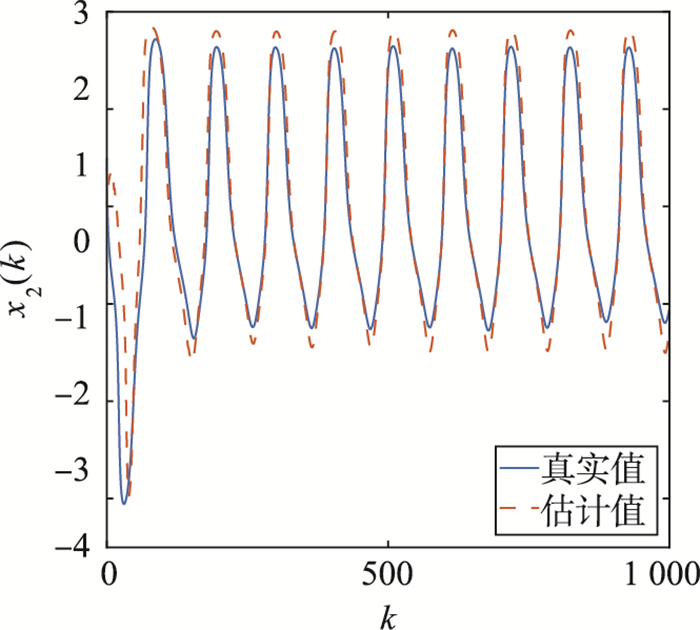
图 2~图 4分别给出了x1(k)、x2(k)、θ(k)的采样值及其截断L=30的估计值.从图 2~图 4可以看出,系统的状态和参数的估计值几乎接近于真实值.因此,定理1设计的基于G-L差分方法的分数阶自适应扩展卡尔曼滤波器算法,能够有效地估计连续时间非线性分数阶系统在截断L=30时的状态和参数,并得到较为满意的状态估计效果.
|
| 图 2 例1中的x1(k)和L=30时的估计值 Fig.2 x1(k) and its estimations with L=30 in Example 1 |
|
| 图 3 例1中的x2(k)和L=30时的估计值 Fig.3 x2(k)and its estimations with L=30 in Example 1 |
|
| 图 4 例1中的θ(k)和L=30时的估计值 Fig.4 θ(k) and its estimations with L=30 in Example 1 |
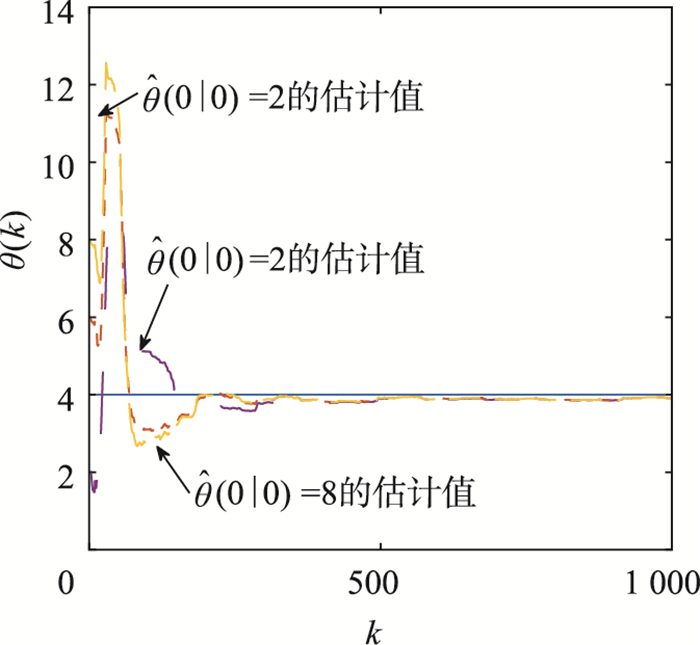
图 5给出了θ(k)及其在截断L=30时不同初始值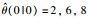
|
| 图 5 例1中的θ(k)和不同初始值时的估计值 Fig.5 θ(k) and its estimations with different initial values in Example 1 |
表 2给出了当截断L=5,10,20,30,40,50,60时,不同阶次的分数阶有色过程噪声状态估计误差的对比结果.从表 2的计算结果可知,状态估计误差随着L的增大而减小,即L越大,分数阶自适应扩展卡尔曼滤波的估计精度越高.
| L | β=0.1 | β=0.3 | β=0.5 | β=0.7 | β=0.9 |
| 5 | 0.398 3 | 0.397 9 | 0.397 4 | 0.397 0 | 0.401 1 |
| 10 | 0.275 3 | 0.275 4 | 0.275 1 | 0.274 5 | 0.272 4 |
| 20 | 0.159 2 | 0.159 8 | 0.160 1 | 0.159 9 | 0.159 3 |
| 30 | 0.148 3 | 0.149 2 | 0.149 8 | 0.150 0 | 0.150 1 |
| 40 | 0.133 9 | 0.134 6 | 0.135 2 | 0.135 4 | 0.135 5 |
| 50 | 0.124 0 | 0.124 5 | 0.125 0 | 0.125 2 | 0.125 1 |
| 60 | 0.117 5 | 0.117 8 | 0.118 1 | 0.118 3 | 0.118 0 |
例2 考虑含有未知参数θ和有色测量噪声v(t)的非线性分数阶系统:
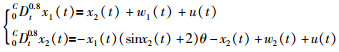
|
(36) |
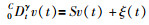
|
(37) |
其中,未知参数、控制输入、状态和过程噪声及其初始值、模型阶次、噪声的协方差矩阵和参数矩阵分别设置为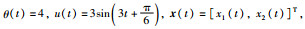
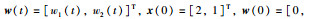
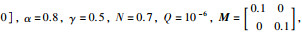
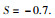
含有测量噪声v(t)的输出方程为z(t)=Hx(t)+v(t),其中H=[1, 1].定理2提出的分数阶自适应扩展卡尔曼滤波器的初始条件设置为σ(0|0)=[0, 0, 0, 0]T,K(0)=[0, 0, 0, 0]T,P(0|0)=I,采样周期Ts和仿真运行时间分别为0.02 s和20 s. 图 6给出了测量值z(k)的采样值. 表 3给出了不同截断L和不同未知参数θ时,定理2中采用的G-L差分的自适应扩展卡尔曼滤波器的状态估计精度以及仿真运行时间比较.结果表明L越大,固定参数θ下的估计误差大致都逐渐减小且运行时间逐渐增长.然而,若截断L太大,会增加算法的计算时间,不利于在实际工程中的应用.所以对于此例中的非线性分数阶系统,同样选择截断L=30作为估计次数是合适的.
|
| 图 6 例2中的测量z(k) Fig.6 Measurement z(k) in Example 2 |
| L | θ=2 | θ=3 | θ=4 | θ=5 | ||||
| 误差 | 运行时间/s | 误差 | 运行时间/s | 误差 | 运行时间/s | 误差 | 运行时间/s | |
| 10 | 0.258 5 | 0.284 5 | 0.249 7 | 0.286 9 | 0.223 9 | 0.272 1 | 0.172 8 | 0.382 3 |
| 20 | 0.160 6 | 0.444 6 | 0.136 9 | 0.442 9 | 0.130 1 | 0.443 9 | 0.124 0 | 0.578 5 |
| 30 | 0.134 3 | 0.704 3 | 0.128 2 | 0.628 7 | 0.124 4 | 0.588 9 | 0.125 3 | 0.619 1 |
| 40 | 0.115 7 | 0.901 2 | 0.126 1 | 0.768 7 | 0.113 3 | 0.901 3 | 0.110 3 | 0.769 5 |
| 50 | 0.101 4 | 1.039 7 | 0.123 3 | 0.939 6 | 0.110 2 | 0.142 5 | 0.104 7 | 0.953 4 |
| 60 | 0.091 4 | 1.117 5 | 0.118 4 | 1.103 2 | 0.109 8 | 1.178 7 | 0.108 6 | 1.141 5 |
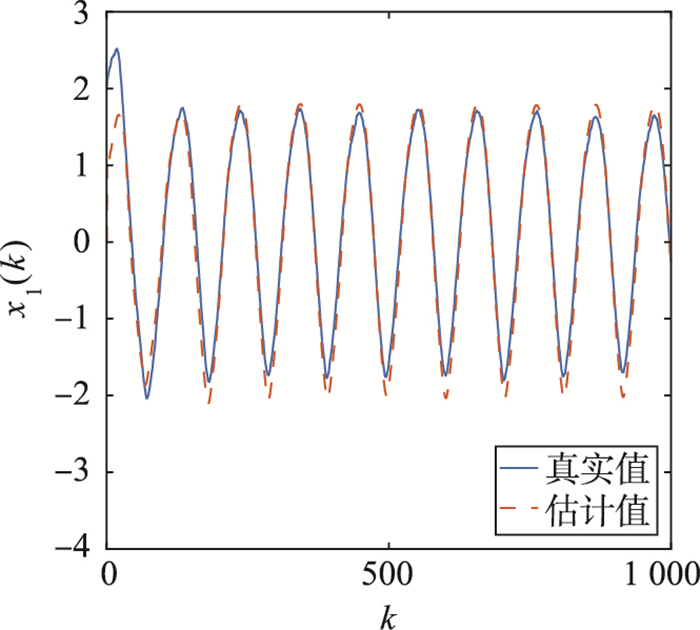
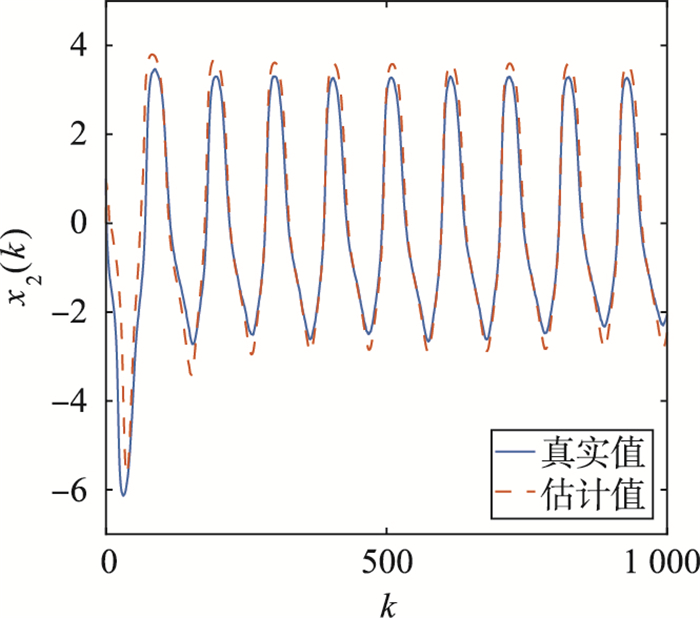
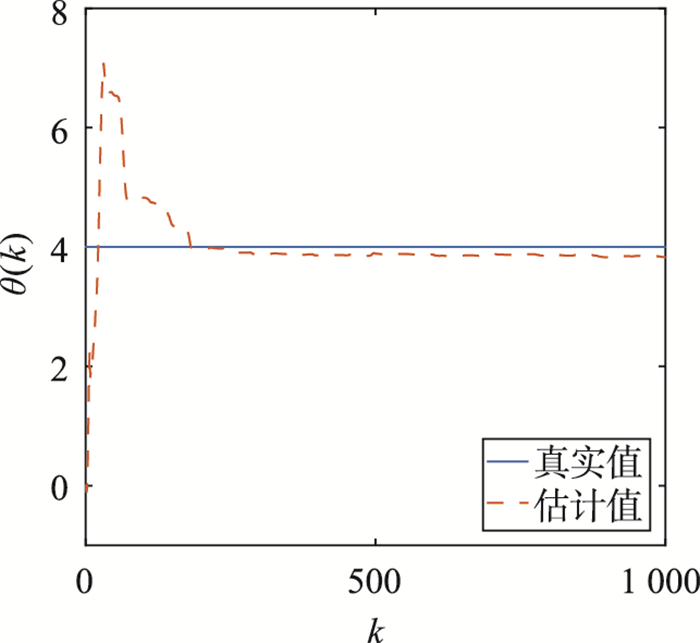
图 7~图 9分别给出了测量噪声为有色噪声时,x1(k)、x2(k)、θ(k)的采样值及其截断L=30的估计值.从图 7~图 9可以看出,分数阶系统状态和参数的估计值接近于真实值.因此,定理2中提出的基于G-L差分方法的分数阶自适应扩展卡尔曼滤波器算法,也能够有效地估计非线性分数阶系统在截断L=30时的状态和未知参数.
|
| 图 7 例2中的x1(k)和L=30时的估计值 Fig.7 x1(k) and its estimations with L=30 in Example 2 |
|
| 图 8 例2中的x2(k)和L=30时的估计值 Fig.8 x2(k)and its estimations with L=30 in Example 2 |
|
| 图 9 例2中的θ(k)和L=30时的估计值 Fig.9 θ(k) and its estimations with L=30 in Example 2 |
图 10给出了θ(k)及其在截断L=30时不同初始值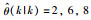
|
| 图 10 例2中的θ(k)和不同初始值时的估计值 Fig.10 θ(k) and its estimations with different initial values in Example 2 |
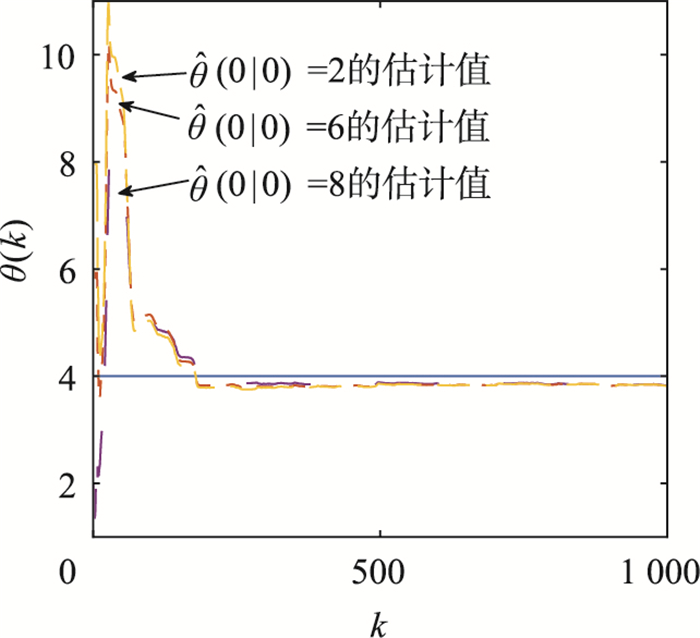
图 11给出了基于G-L差分定义在截断L=30时采样周期从Ts =0.01 s到Ts =0.5 s的估计误差,其中,Ts为0.01 s,0.02 s,…,0.5 s.从图 11中可以看出基于G-L差分定义的分数阶自适应卡尔曼滤波器在较小周期Ts内有较高的估计精度,但是随着周期Ts的增大,定理2中给出的算法无法有效的估计系统状态.因此,需要合理的选择采样周期保证算法的稳定性.
|
| 图 11 例2中的L=30时的估计误差值 Fig.11 Estimation error with L=30 in Example 2 |
本文研究含有分数阶有色过程噪声或分数阶有色测量噪声和未知参数的连续时间非线性分数阶系统状态估计和参数估计问题.通过1阶泰勒展开公式对非线性函数进行线性化,利用G-L差分方法对连续时间分数阶系统再进行离散化.通过构建关于状态向量、有色噪声和未知参数的增广向量的方法,处理非线性分数阶系统中存在的有色过程噪声与未知参数的问题.给出了自适应分数阶扩展卡尔曼滤波器的五个迭代公式实现了状态和参数的估计.此外,本文也讨论了实际工程应用中分数阶扩展卡尔曼滤波器历史信息的有效截断问题,以及讨论了合理选择截断L的方法.
| [1] |
朱呈祥, 邹云.
分数阶控制研究综述[J]. 控制与决策, 2009, 24(2): 161–169.
Zhu C X, Zou Y. Summary of research on fractional-order control[J]. Control and Decision, 2009, 24(2): 161–169. DOI:10.3321/j.issn:1001-0920.2009.02.001 |
| [2] |
赵志诚, 张博, 刘志远, 等.
一种分数阶系统内模PID控制器设计方法[J]. 信息与控制, 2014, 43(2): 129–133.
Zhao Z C, Zhang B, Liu Z Y, et al. Design method for IMC-PID controller for fractional order system[J]. Information and Control, 2014, 43(2): 129–133. |
| [3] |
蔡伟, 陈文.
复杂介质中任意阶频率依赖耗散声波的分数阶导数模型[J]. 力学学报, 2016, 48(6): 1265–1280.
Cai W, Chen W. Fractional derivative modelling of frequency-dependent dissipative mechanism for wave propagation in complex media[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(6): 1265–1280. |
| [4] |
王东风, 孟丽.
基于粒子群和辅助变量法的分数阶系统辨识[J]. 信息与控制, 2016, 45(3): 287–293.
Wang D F, Meng L. Identification of fractional order system based on PSO and recursive instrumental variable methods[J]. Information and Control, 2016, 45(3): 287–293. |
| [5] | Yu D, Mao Z Z, Yuan P, et al. Recursive parameter estimation for Hammerstein-Wiener systems using modified EKF algorithm[J]. ISA Transactions, 2017, 70: 104–115. DOI:10.1016/j.isatra.2017.05.012 |
| [6] | Xiao M L, Zhang Y B, Wang Z H, et al. An adaptive three-stage extended Kalman filter for nonlinear discrete-time system in presence of unknown inputs[J]. ISA Transactions, 2018, 75: 101–117. DOI:10.1016/j.isatra.2018.02.007 |
| [7] | Olivier A, Smyth A W. A marginalized unscented Kalman filter for efficient parameter estimation with applications to finite element models[J]. Computer Methods in Applied Mechanics and Engineering, 2018, 339: 615–643. DOI:10.1016/j.cma.2018.05.014 |
| [8] | Gao S S, Hu G G, Zhong Y M. Windowing and random weighting-based adaptive unscented Kalman filter[J]. International Journal of Adaptive Control and Signal Processing, 2015, 29(2): 201–223. DOI:10.1002/acs.2467 |
| [9] | Wang J L, Wang J H, Zhang D X, et al. Kalman filtering through the feedback adaption of prior error covariance[J]. Signal Processing, 2018, 152: 47–53. DOI:10.1016/j.sigpro.2018.05.011 |
| [10] |
魏克新, 陈峭岩.
基于多模型自适应卡尔曼滤波器的电动汽车电池荷电状态估计[J]. 中国电机工程学报, 2012, 32(31): 19–26.
Wei K X, Chen Q Y. Electric vehicle battery SOC estimation based on multi-model adaptive Kalman filter[J]. Proceedings of the CSEE, 2012, 32(31): 19–26. |
| [11] |
吴广鑫, 姜力, 谢宗武, 等.
基于自适应固定滞后卡尔曼平滑器的状态观测器在假手上的应用[J]. 机器人, 2018, 40(4): 474–478.
Wu G X, Jiang L, Xie Z W, et al. The application of a state observer based on adaptive fixed-lag Kalman smoother to prosthetic hand[J]. Robot, 2018, 40(4): 474–478. |
| [12] | Sierociuk D, Dzielinski A. Fractional Kalman filter algorithm for the states, parameters and order of fractional system estimation[J]. International Journal of Applied Mathematics and Computer Science, 2006, 16(1): 129–140. |
| [13] | Chen X, Zhang J, Ma T. Parameter estimation and topology identification of uncertain general fractional-order complex dynamical networks with time delay[J]. IEEE/CAA Journal of Automatica Sinica, 2016, 3(3): 295–303. DOI:10.1109/JAS.2016.7508805 |
| [14] | Sun Y H, Wang Y, Wu X P, et al. Robust extended fractional Kalman filter for nonlinear fractional system with missing measurements[J]. Journal of the Franklin Institute-Engineering and Applied Mathematics, 2018, 355(1): 361–380. DOI:10.1016/j.jfranklin.2017.10.030 |
| [15] | Ramezani A, Safarinejadian B. A modified fractional-order unscented Kalman filter for nonlinear fractional-order systems[J]. Circuit system and signal processing, 2018, 37(9): 3756–3784. DOI:10.1007/s00034-017-0729-9 |
| [16] | Wang X H, Ding F. Joint estimation of states and parameters for an input nonlinear state-space system with colored noise using the filtering technique[J]. Circuits Systems and Signal Processing, 2016, 35(2): 481–500. DOI:10.1007/s00034-015-0071-z |
| [17] | Sierociuk D, Ziubinski P. Fractional order estimation schemes for fractional and integer order systems with constant and variable fractional order colored noise[J]. Circuits, Systems, and Signal Processing, 2014, 33(12): 3861–3882. DOI:10.1007/s00034-014-9835-0 |
| [18] |
孙永辉, 高振阳, 卫志农, 等.
一种考虑非高斯Lévy量测噪声下的改进分数阶卡尔曼滤波[J]. 控制与决策, 2016, 31(3): 547–550.
Sun Y H, Gao Z Y, Wei Z N, et al. An improved Kalman filter for fractional order system with non-Gaussian measurement Lévy noise[J]. Control and Decision, 2016, 31(3): 547–550. |
| [19] | Sun Y H, Wu X P, Cao J D, et al. Fractional extended Kalman filtering for non-linear fractional system with Lévy noises[J]. IET Control Theory and Applications, 2017, 11(3): 349–358. DOI:10.1049/iet-cta.2016.1041 |
| [20] | Yang C, Gao Z, Liu F H. Kalman filters for linear continuous-time fractional-order systems involving coloured noises using fractional-order average derivative[J]. IET Control Theory and Applications, 2018, 12(4): 456–465. DOI:10.1049/iet-cta.2017.0817 |
| [21] | Gao Z. Fractional-order Kalman filters for continuous-time fractional-order systems involving colored process and measurement noises[J]. Journal of the Franklin Institute-Engineering and Applied Mathematics, 2018, 355(2): 922–948. DOI:10.1016/j.jfranklin.2017.11.037 |
| [22] |
吴强, 黄建华.
分数阶微积分[M]. 北京: 清华大学出版社, 2016: 74-77.
Wu Q, Huang J H. Fractional-order calculus[M]. Beijing: Tsinghua University press, 2016: 74-77. |
| [23] | Sadeghian H, Salarieh H, Alasty A, et al. On the fractional-order extended Kalman filter and its application to chaotic cryptography in noisy environment[J]. Applied Mathematical Modelling, 2014, 38(3): 961–973. DOI:10.1016/j.apm.2013.07.011 |



