2. 江西省先进控制与优化重点实验室, 江西 南昌 330013
2. The Jiangxi Province Key Laboratory of Advanced Control and Optimization, Nanchang 330013, China
0 引言
随着多智能体研究的不断深入,其一致性控制受到了广泛关注,例如群集控制、编队控制和跟踪问题等,近年来许多研究者在这些方面展开了一系列研究[1-3].其中通过智能体之间的交互信息来设计控制算法使跟随智能体与领航智能体的状态保持一致的领导—跟随一致性控制,更是因其通信成本低、鲁棒性强、效率高等优点而受到学术界的推崇而且成果显著[4-7].但是,这些一致性控制方法大多集中于线性多智能体系统中,而大多数实际中的多智能体系统具有更为复杂的非线性.因此,非线性多智能体系统的一致性控制更具有现实意义,从而吸引了诸多学者关注[8-11].文[8]在一个具有代表性的一般非线性模型的基础上,提出了多智能体系统一致性的几个基本准则.文[9]针对非线性条件进行了研究.在上述文献的基础上,文[10]研究了二阶非线性多智能体系统的事件驱动控制.
正是因为多智能体系统存在非线性动态和干扰等因素,所以与上述这些控制协议相比,滑模控制是应对这些不利因素最有效的方法之一.滑模控制是一种非线性控制方法,通过使用一种不连续控制信号并且让系统滑入预定的转换面上来改变系统的动力学模型.与其它控制方法相比,滑模控制由于其简单性、对干扰的高鲁棒性和对系统参数的低敏感性而促使学者将其应用于多智能体系统中[11-12].文[13]利用滑模控制来解决带有时延的非线性多智能体系统的一致性问题.文[14]中研究了基于终端滑模控制的有向通信拓扑的二阶非线性多智能体系统的有限时间领导—跟随一致性的问题.文[15]将终端滑模控制应用于有外界干扰的非线性二阶多智能体系统中,实现了系统的有限时间一致性.文[16]在文[14-15]的基础上,针对多智能体系统应用于实际过程中的非线性动态和时延等问题,提出了基于滑模控制的解决方案.
上述文献中对于外部干扰的解决方法不尽相同,但均可以减小或是消除干扰对系统的影响.但实际中,由于环境等影响,干扰往往是未知的.所以,学者们从其它角度出发,提出了更多关于消除未知外部扰动的思考及研究成果[17-21].文[17]提出了一种不连续积分滑模面,极大程度上减小了干扰估计的误差,从而抑制未知干扰对多智能体系统的影响.文[18]针对外部扰动提出了一种自适应律来对其进行估计.文[19]提出了一种分布式观测器,将得到的干扰估计应用于系统的事件触发控制策略中,并在外部干扰未知的情况下实现了多智能体系统有限时间一致.文[20]提出了一种有限时间干扰观测器来实现对未知扰动的估计,实现了跟随者状态信息的可测.文[21]在文[20]的基础上,针对非匹配扰动,将非奇异终端滑模控制和干扰观测器相结合,保证了系统在非匹配扰动下的一致性.
考虑目前具有外部扰动的非线性多智能体系统基于滑模控制一致性的研究成果,大部分都集中于滑模面设计或者控制协议设计,多没有考虑到扰动的估计速度,而扰动的估计速度可以大幅度影响系统的性能.本文围绕带有未知外部扰动的二阶非线性多智能体系统的一致性问题展开研究.主要贡献可概括为如下两个方面:首先,针对由恒定增益所引起峰值问题,提出了一种带有时变增益的有限时间干扰观测器,可实现对外部扰动的快速估计,后续仿真部分验证了本文所提观测器在估计速度方面的优越性;其次,设计了一类积分超螺旋滑模控制协议,并与文[17]所提出的滑模控制协议进行了对比,结果表明本文的控制方法可更有效抑制抖振现象,而且积分滑模面的分数幂被封装在积分运算中,其一阶导数中不会产生负分数幂,即避免了传统滑模面的奇异性问题;最后论文通过将有限时间干扰观测器和积分滑模控制相结合,实现了带有扰动的多智能体系统快速抗扰一致性,在利用李亚普诺夫函数证明其稳定性的基础上,通过Matlab数值仿真进一步验证了其有效性.
在本文中,*表示矩阵对称部分,Rn×m代表n×m维的欧氏空间,sgn x代表sign x,sigγ(x)代表|x| γsgn x,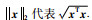
考虑一个领导—跟随多智能体系统,它包含一个领导者和h个跟随者智能体多智能体系统的通信拓扑可以用有向图G=(v,ε)来表示,其中:v={0,1,2,…,h}是智能体的集合,ε∈v×v表示无自循环的有向边集.定义A =(aij)∈R(h+1)×(h+1)为其邻接矩阵,(i,j)∈ε表示aij=1,(i,j) 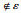
假设1 对于一个领导跟随多智能体系统,其通信拓扑图至少含有一个生成树.
1.2 相关引理考虑一个非线性系统为
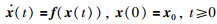
|
(1) |
其中,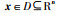
定义1[6] 假设原点为系统(1)的平衡点,如果存在关于原点的开邻域D0⊆D和连续稳定时间函数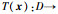
1) 有限时间收敛:对于任意
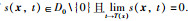
2) 李亚普洛夫稳定:对于任意关于原点的开集D1⊆D0,存在包含原点的集合D2⊆D使得对于任意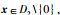
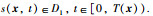
那么原点为该系统的有限时间稳定平衡点.
如果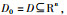
引理1[6] 对于系统(1),存在一个连续可微正定李亚普诺夫函数V(x)及常数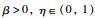
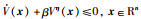
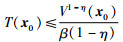
|
(2) |
引理2[6] 考虑如式(1)所示的系统,如果存在一系列权重系数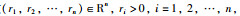
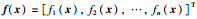
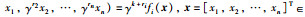
考虑到多智能体系统拥有一个领导者和h个跟随者.网络中领导者的动力学模型为
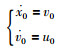
|
(3) |
式中,x0表示领航者的位置,v0表示其速度,u0表示控制输入.
跟随者的动力学模型为
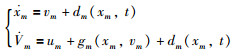
|
(4) |
其中,xm和ym分别表示跟随者m的位置和速度,m=1, 2, …, h, um,表示控制输入,gm(xm, vm)表示为非线性动态,dm(xm, t)代表匹配干扰.
本文控制目标是在所有跟随者的外部扰动未知情况下,设计一致性控制协议,保证所有跟随者在有限时间内达到并维持与领导者的一致性.
2 主要结果 2.1 时变有限时间干扰观测器设计假设2 dm(xm,t)及其一阶微分是有界的,即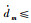
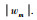
因为多智能体系统中存在外部扰动,会影响到系统性能.为提高系统的抗扰能力,引入有限时间干扰观测器来估计扰动,并将扰动的估值作为补偿加入控制协议中.
在假设2成立的条件下,本文给出的时变有限时间干扰观测器如下:
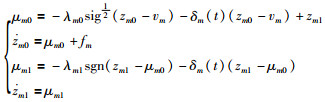
|
(5) |
其中,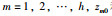
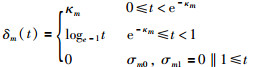
|
(6) |
其中,κm为正常数.
定义估计误差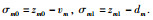
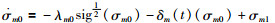
|
(7) |
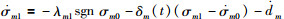
|
(8) |
定理1 对于多智能体系统,设计有限时间干扰观测器(5),且观测器的参数满足
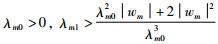
|
(9) |
那么估计误差方程(7)和(8)是在有限时间稳定的.
证 选取李亚普诺夫函数
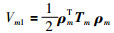
|
(10) |
其中
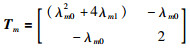
|
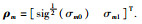
求其一阶微分可得:
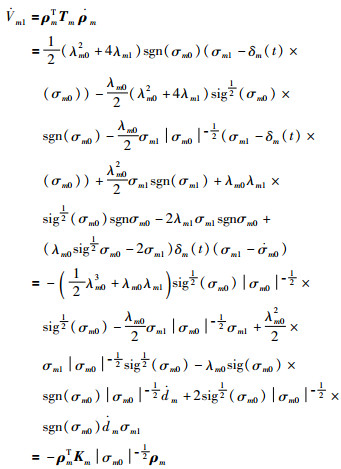
|
(11) |
其中,
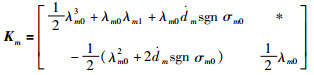
|
且当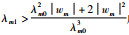
同时,因为Tm为正定矩阵,可知
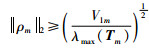
|
又有
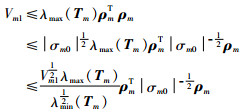
|
(12) |
式中,λmax(Tm)和λmin(Tm)分别为Tm的最大特征值及最小特征值.
式(12)可变换为
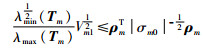
|
(13) |
此时,将式(13)代入式(11)中可得
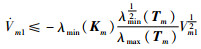
|
(14) |
于是,由引理1得知,时变有限时间干扰观测器可以在有限时间内实现对扰动的估计,即定理1得证.
2.2 基于超螺旋积分滑模一致性控制此时,定义一致性误差:
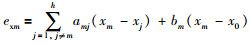
|
(15) |
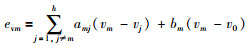
|
(16) |
其中,exm是位置误差,evm是速度误差.
为确保状态误差exm和evm收敛,考虑跟随者m的积分滑模面如下:
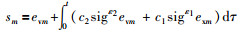
|
(17) |
其中,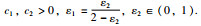
定理2 在假设1和2成立的条件下,对于领导跟随系统来说,选取式(17)作为跟随者的积分滑模面,在干扰观测器的基础上设计如下的一致性协议:
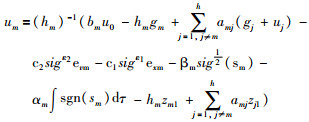
|
(18) |
其中,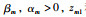
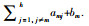
证 求滑模面(17)的一阶导并代入式(15),(16)及(17)得:
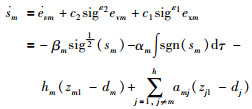
|
(19) |
为方便证明滑模面的稳定性,先对式(19)进行化简并重写为
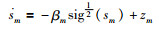
|
(20) |
式中,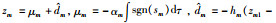
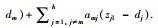
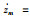
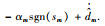
因为干扰观测器是有限时间收敛的,那么肯定存在一个收敛时间t1,换而言之,当t≥t1时,存在一常数ξ且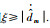
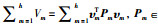
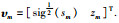
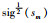
求υm的一阶导:
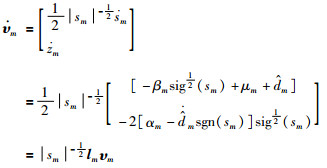
|
(21) |
其中,
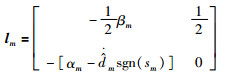
|
此时,当βm>0且αm>ξ>0成立时,矩阵lm的特征值都具有负实部,所以矩阵 lm是Hurwitz矩阵.
对求一阶导为
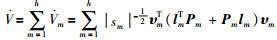
|
(22) |
因为矩阵lm是Hurwitz矩阵,有对于任意给定的对称正定矩阵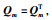
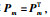
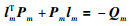
|
(23) |
那么,式(22)可以变为
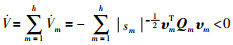
|
(24) |
因为Pm是正定的,所以有:
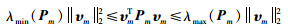
|
(25) |
根据不等式(25),可进一步得到:
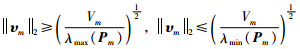
|
(26) |
式中,λmax(Pm)和λmin(Pm)分别为Pm的最大特征值和最小特征值.
由式(26)知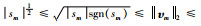
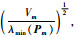
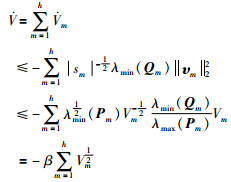
|
(27) |
式中,
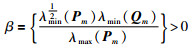
|
因为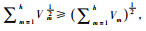
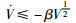
|
(28) |
根据引理1得知,所有滑模面是在有限时间内稳定的,即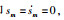
注1 为了遏制抖振对系统的影响,很多文献采用饱和函数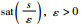
接下来需要证明一致性误差能够在有限时间内收敛到0,当系统轨迹抵达滑模面,根据积分滑模面的性质及式(19)得到一致性误差方程为
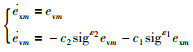
|
(29) |
选取李亚普诺夫函数:
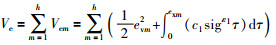
|
(30) |
求其一阶导并将式(29)带入:
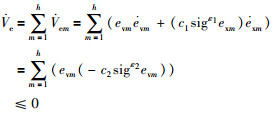
|
(31) |
考虑如下向量场:
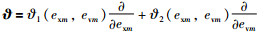
|
(32) |
其中,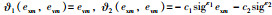
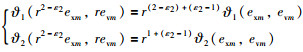
|
(33) |
也就是说向量场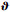
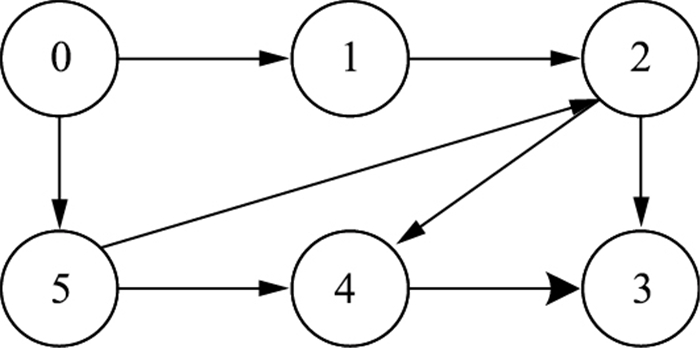
本文在Matlab软件上对所提出的算法进行仿真验证.本文考虑由1个领导者和5个跟随者组成的多智能体系统,其拓扑结构如图 1.
|
| 图 1 系统的拓扑结构 Fig.1 Topology of system |
根据多智能体系统式(3)和(4),假设非线性动态为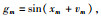
设置滑模面的参数
|
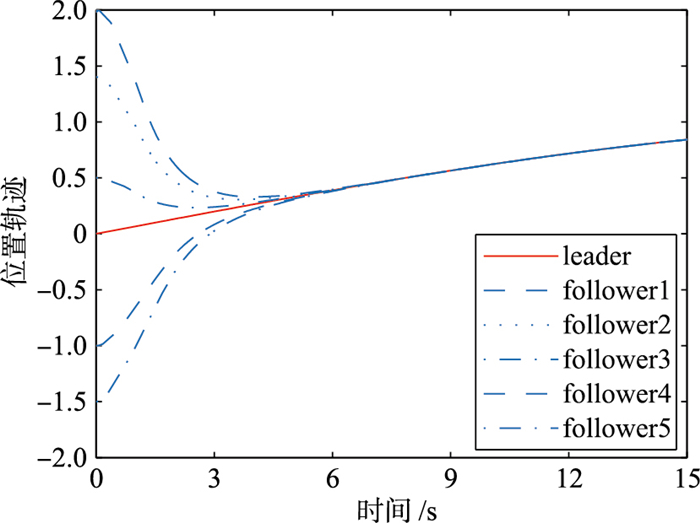
| 图 2 领导者与跟随者的位置轨迹 Fig.2 Position tracking of leader and follower |
|
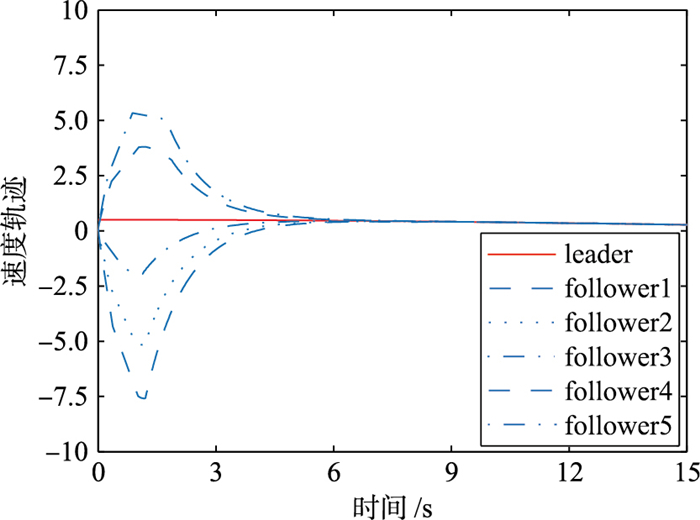
| 图 3 领导者与跟随者的速度轨迹 Fig.3 Speed tracking of leader and follower |
|
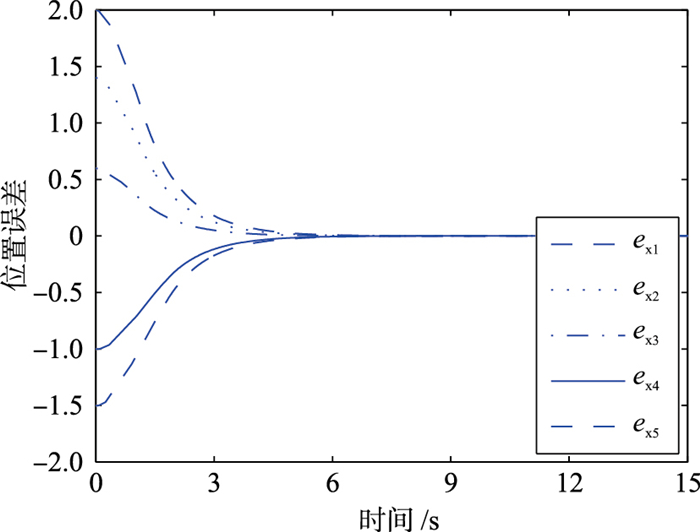
| 图 4 跟随者的位置误差轨迹 Fig.4 Position error tracking of follower |
|
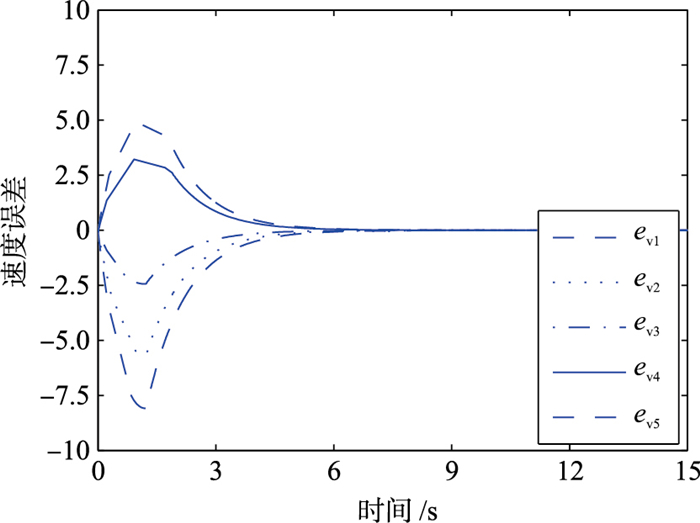
| 图 5 跟随者的速度误差轨迹 Fig.5 Speed error tracking of follower |
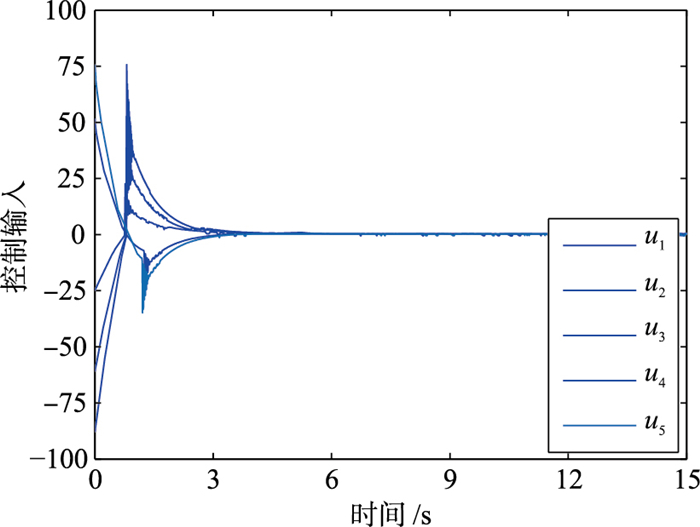
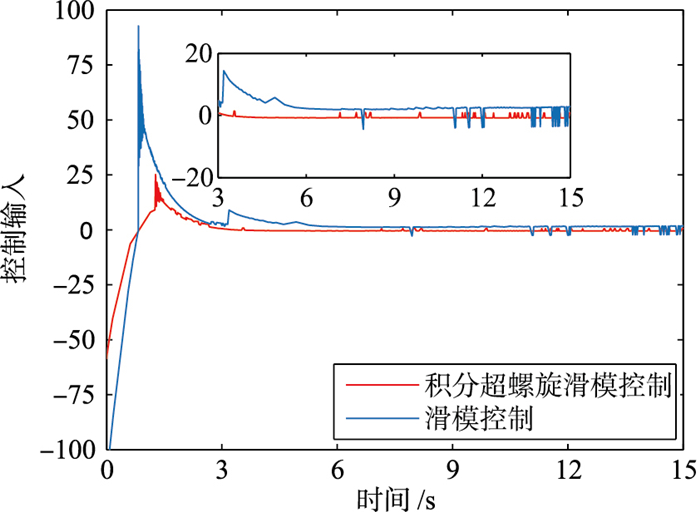
图 6是各个跟随智能体的控制输入,可清楚地看出控制信号在控制协议(18)的作用下较为平滑地运行,也说明了抖振现象被抑制.图 7为同一跟随智能体在不同控制协议下的控制输入,因为所提出的连续控制协议能够更好地抑制抖振现象,所以本文的控制协议下的控制输入比文[17]的更为平滑.
|
| 图 6 跟随者的控制输入 Fig.6 Control input of follower |
|
| 图 7 两种控制协议的控制输入 Fig.7 Control input of two control protocol |
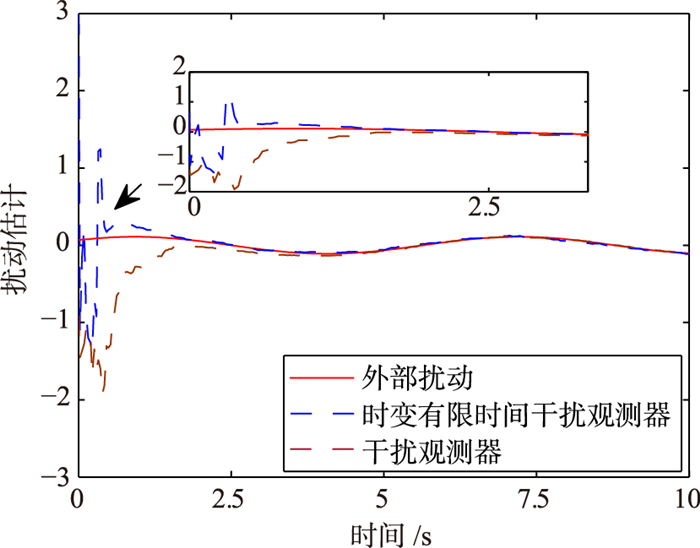
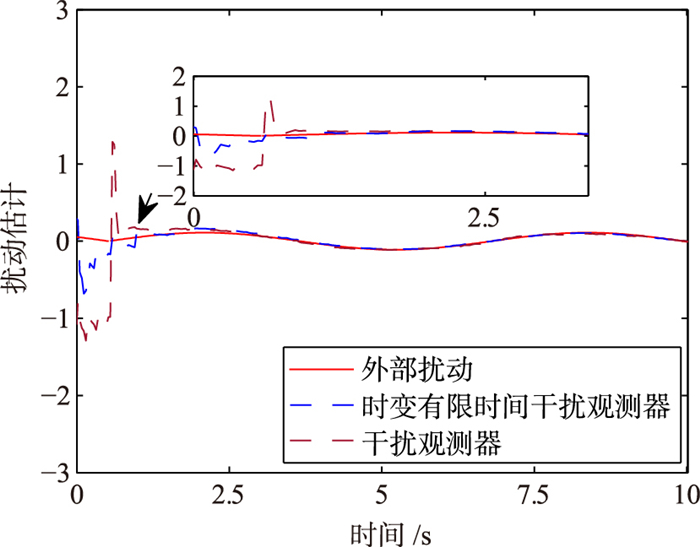
图 8、图 9绘制了在观测器初始参数一致的情况下,本文所提出的干扰观测器与文[21]中所提出的干扰观测器对未知外部扰动的估计曲线.两图中,分别使用,作为外部干扰.由图可知,两者都能够实现对扰动的估计,但本文的时变干扰观测器能明显地降低峰值.
|
| 图 8 两种观测器对d1的估计 Fig.8 Estimation of d1 |
|
| 图 9 两种观测器对d2的估计 Fig.9 Estimation of d2 |
表 1展现了相同观测器参数下两种方法对,估计的耗时.结果表明,本文所提出的时变有限时间干扰观测器在面对未知的外部扰动时,能够更快地实现扰动估计.
| 对d1的估计用时/s | 对d2的估计用时/s | |
| 时变有限时间干扰观测器 | 1.434 | 0.867 |
| 非线性干扰观测器 | 2.338 | 1.458 |
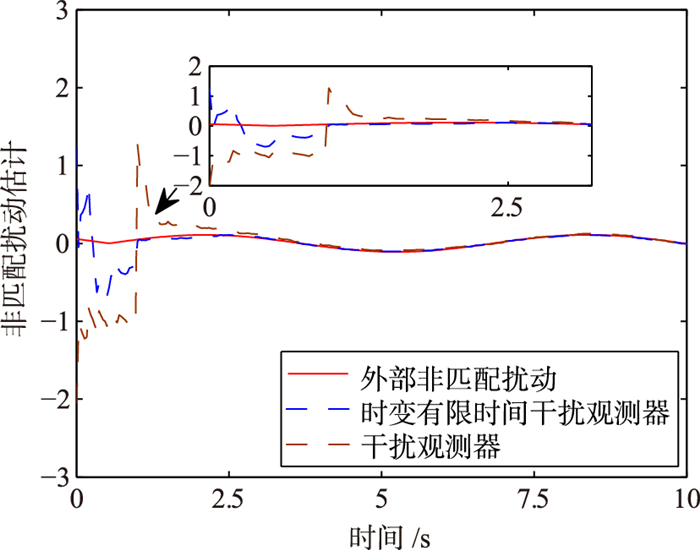
因为文[21]中的观测器可以对匹配或非匹配扰动进行估计,所以为证明本文设计的观测器的优越性,在此通过增加对非匹配扰动的仿真来说明所提观测器在面对非匹配扰动时依然可以降低峰值并加快估计速度.从图 10中可以明显看出在面对非匹配扰动时,本文所给出的观测器的收敛时间为t=0.974 s,而文[21]中的观测器的收敛时间为t=2.534 s,而且本文观测器的峰值相对较小.
|
| 图 10 两种观测器对非匹配扰动的估计 Fig.10 Estimation of Mismatched Disturbance |
研究了带有外部干扰的二阶非线性多智能体系统的有限时间一致性问题.首先,采用了一种带有时变增益的有限时间干扰观测器,随后在该观测器的基础上设计了超螺旋积分滑模控制协议实现了系统的有限时间一致,该观测器的最大特点是通过引入时变增益解决了初始状态下观测器收敛速度过慢的问题,能够更快地实现干扰估计.运用图论,李亚普诺夫原理等证明了在该控制协议能够实现非线性系统的快速抗扰一致.最后,Matlab仿真结果进一步表明了该控制协议的有效性及较好的抖振抑制性能,同时通过与已有文献中提出的有限时间干扰观测器相比,验证了所提出的时变有限时间干扰观测器在干扰估计速度方面的优越性.
| [1] | Peng Z, Wen G, RahmaniI A, et al. Distributed consensus-based formation control for multiple non-holonomic mobile robots with a specified reference trajectory[J]. International Journal of Systems Science, 2015, 46(8): 1447–1457. |
| [2] | Lin P, Ren W, Gao H. Distributed velocity-constrained consensus of discrete-time multi-agent systems with non-convex constraints, switching topologies, and delays[J]. IEEE Transactions on Automatic Control, 2017, 62(11): 5788–5794. DOI:10.1109/TAC.2016.2637005 |
| [3] |
陈世明, 李慧敏, 谢竟, 等.
基于社团划分的多智能体蜂拥控制算法[J]. 信息与控制, 2013, 42(5): 536–541.
Chen S M, Li M H, Xie J, et al. Flocking control algorithm of multiple agents based on community division[J]. Information and Control, 2013, 42(5): 536–541. |
| [4] | Olfati-Saber R, Fax J A, Murray R M. Consensus and co-operation in networked multi-agent systems[J]. Proceedings of the IEEE, 2007, 95(1): 215–233. DOI:10.1109/JPROC.2006.887293 |
| [5] |
金治群, 牛玉刚, 邹媛媛.
带有滑模观测器的多智能体一致性控制[J]. 控制理论与应用, 2017, 34(2): 251–259.
Jin Z Q, Niu Y G, Zhou Y Y. Consensus for multi-agent systems with sliding-mode observer[J]. Control Theory&Application, 2017, 34(2): 251–259. |
| [6] | Hong Y, Xu Y, Huang J. Finite-time control for robot manipulators[J]. Systems&control letters, 2002, 46(4): 243–253. |
| [7] | Li S, Du H, Lin X. Finite-time consensus algorithm for multi-agent systems with double-integrator dynamics[J]. Automatica, 2011, 47(8): 1706–1712. DOI:10.1016/j.automatica.2011.02.045 |
| [8] | Du H, He Y, Cheng Y. Finite-time synchronization of a class of second-order nonlinear multi-agent systems using output feedback control[J]. IEEE Transactions on Circuits and Systems I:Regular Papers, 2014, 61(6): 1778–1788. DOI:10.1109/TCSI.2013.2295012 |
| [9] | Li W, Zhou H, Liu Z W, et al. Impulsive coordination of nonlinear multi-agent systems with multiple leaders and stochastic disturbance[J]. Neurocomputing, 2016, 171: 73–81. DOI:10.1016/j.neucom.2015.06.015 |
| [10] |
邵浩宇, 胡爱花.
基于事件驱动控制的非线性多智能体的一致性[J]. 信息与控制, 2015, 44(1): 38–42, 50.
Shao H Y, Hu A H. Consensus of nonlinear multi-agent systems with event-triggered control[J]. Information and Control, 2015, 44(1): 38–42, 50. |
| [11] | Yu S, Long X. Finite-time consensus for second-order multi-agent systems with disturbances by integral sliding mode[J]. Automatica, 2015, 54: 158–165. DOI:10.1016/j.automatica.2015.02.001 |
| [12] | Khoo S, Xie L, Man Z. Robust finite-time consensus tracking algorithm for multirobot systems[J]. IEEE/ASME transactions on mechatronics, 2009, 14(2): 219–228. DOI:10.1109/TMECH.2009.2014057 |
| [13] | Zhang J, Lyu M, Shen T, et al. Sliding mode control for a class of nonlinear multi-agent system with time delay and uncertainties[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 865–875. DOI:10.1109/TIE.2017.2701777 |
| [14] | Ren C E, Chen C L P. Sliding mode leader-following consensus controllers for second-order non-linear multi-agent systems[J]. IET Control Theory&Applications, 2015, 9(10): 1544–1552. |
| [15] |
袁雷, 肖飞, 沈建清, 等.
基于扰动观测器的不确定非线性系统非奇异终端滑模控制[J]. 控制与决策, 2014, 29(2): 353–357.
Yuan L, Xiao F, Shen J Q, et al. Nonsingular terminal sliding mode control with disturbance observer for uncertain nonlinear systems[J]. Control and Decision, 2014, 29(2): 353–357. |
| [16] | Zhang J, Lyu M, Shen T, et al. Sliding mode control for a class of nonlinear multi-agent system with time delay and uncertainties[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 865–875. DOI:10.1109/TIE.2017.2701777 |
| [17] | Tian B, Zuo Z, Wang H. Leader-follower fixed-time consensus of multi-agent systems with high-order integrator dynamics[J]. International Journal of Control, 2017, 90(7): 1420–1427. DOI:10.1080/00207179.2016.1207101 |
| [18] | Wang W, Wen C, Huang J. Distributed adaptive asymptotically consensus tracking control of nonlinear multi-agent systems with unknown parameters and uncertain disturbances[J]. Automatica, 2017, 77: 133–142. DOI:10.1016/j.automatica.2016.11.019 |
| [19] | Huang Y, Jia Y. Fixed-time consensus tracking control for second-order multi-agent systems with bounded input uncertainties via NFFTSM[J]. IET Control Theory&Applications, 2017, 11(16): 2900–2909. |
| [20] | Shtessel Y B, Shkolnikov I A, Levant A. Smooth second-order sliding modes:Missile guidance application[J]. Automatica, 2007, 43(8): 1470–1476. DOI:10.1016/j.automatica.2007.01.008 |
| [21] | Wang X, Li S, Yu X, et al. Distributed active anti-disturbance consensus for leader-follower higher-order multi-agent systems with mismatched disturbances[J]. IEEE Transactions on Automatic Control, 2017, 62(11): 5795–5801. DOI:10.1109/TAC.2016.2638966 |



