2. 南京理工大学自动化学院, 江苏 南京 210094
2. School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China
0 引言
由于信号测量及其传递过程需要一定的时间,所以时滞是工程实际中广泛存在的一种现象[1].无论是在工程学和物理学中,还是在生物学和经济学中,大量的系统均可以建模成时滞系统进行分析研究[2-3].因此,时滞系统的研究具有十分重要的理论意义与实际应用价值.近几十年来,时滞系统的研究已经吸引了国内外众多学者的广泛关注.从本质上来说,时滞系统是一种特殊的无限维系统.它的一个重要特性是,其状态变化不仅依赖于当前的状态,也依赖于过去的状态.因而,与无时滞的系统相比,时滞系统具有更加复杂的动态特性.
毫无疑问,稳定性是时滞系统研究首先需要考虑的问题.时滞的存在,往往会导致系统的控制性能下降,甚至使原本已经稳定的系统丧失稳定性能.而另一方面,有时在系统中人为引入时滞环节,可以使不稳定的系统变得稳定[1].因此,时滞系统稳定性研究的一个重要内容是,获得保守性尽可能小的稳定性条件,从而判定时滞系统在时滞变量变化多大的范围内保持稳定,即求取时滞系统稳定时时滞变量最大的变化范围[4-5].目前研究线性时滞系统稳定性问题主要有两种途径:一种是频域法[6-8],一种是时域法.针对时变时滞系统,人们通常采用时域法.在时域法中,相对于Lyapunov-Razumikhin泛函方法[9],Lyapunov-Krasovskii(L-K)泛函方法充分考虑了系统中的时滞信息,通常可以得到保守性更小的判别条件.因此,L-K泛函方法已经成为目前研究线性时滞系统稳定性问题的一个强有力的工具[10-12].
本文主要讨论式(1)的线性时滞系统(为了控制文章篇幅,这里只讨论连续系统):
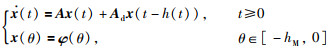
|
(1) |
其中,x(t)∈Rn是状态变量;A和Ad是系统矩阵;φ(θ)是初始条件;时滞变量h(t)满足约束条件:
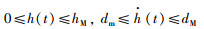
|
(2) |
其中,hM,dm和dM为已知标量.这里的时滞变量h(t)满足的约束条件(2)是目前文献中研究较多的一种情况,即在h(t)一定时间范围里变化且其变化速率的上下限已知.其实还存在其它情况的约束条件,如时滞变量h(t)变化下限不为0,时滞变量h(t)变化速率上下限均不可知或部分可知.这些约束条件的情况这里不去讨论,感兴趣的读者可以参考文[13-14].另外,对于其它类型的时滞系统(如定常时滞系统,多时滞系统等),这里也不加以讨论.
为了研究时滞系统(1)稳定性,目前文献中构造的L-K泛函通常包含积分项[3, 15]:
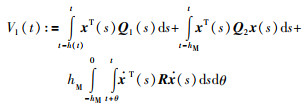
|
其中,Q1、Q2和R是待定的正定矩阵.将V1(t)对时间求导后会出现积分项:
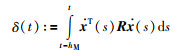
|
(3) |
直接根据δ(t)无法推导出具有线性矩阵不等式(linear matrix inequality,LMI)形式的稳定性条件.因此,如何进一步处理该积分项δ(t),成为获得松弛稳定性条件的关键.早期人们通常采用交叉项技术(如Park不等式[16]和Moon不等式[10])和模型转换技术[11, 17].然而,基于前者技术得到的稳定性条件通常具有较大的保守性;基于后者技术,一方面存在需要进行模型转换的麻烦,另一方面存在转换后的模型不一定等价于原模型的不足.针对上述问题,文[18-21]提出了自由权矩阵技术.该技术基于Newton-Leibniz公式,通过引入一些自由变量构造零等式,并将零等式加到L-K泛函的导数中去,从而成功地避开了应用交叉项和模型转换技术时遇到的麻烦,有效地降低了所获稳定性条件的保守性.需要注意的是,在应用自由权矩阵技术构造零等式时容易引入过多的自由变量,这些变量对于降低保守性不起任何作用,反而会增加求解LMI的计算负担.
目前人们在处理积分项时广泛采用的是积分不等式方法[1, 15].该方法直接对积分项δ(t)进行缩放,实现了从向量乘积的积分到向量积分的乘积转换.在众多积分不等式中,Jensen不等式是提出最早、应用也最为广泛的不等式[1].若将其应用于积分项δ(t),则有:
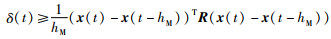
|
(4) |
从式(4)可以看出,积分项δ(t)的下界估值由状态向量的端点x(t)和x(t-hM)表示,据此不难得到具有LMI形式的稳定性条件.为了克服Jensen不等式固有的保守性[22],2013年Seuret等基于Wirtinger不等式提出了Wirtinger-based积分不等式[15],该积分不等式给出了比Jensen积分不等式更加精确的边界估值.紧接着,2015年Seuret等又提出了比Jensen求和不等式更加精确的Wirtinger-based求和不等式[23]. Wirtinger-based积分/求和不等式的相继提出,激发了国内外学者研究线性时滞系统稳定性问题的热情,有力地推动了积分/求和不等式理论的发展.短短几年时间,新的积分/求和不等式不断被提出,如Bessel-Legendre不等式[24]、Auxiliary-function-based不等式[25-28]、Free-matrix-based不等式[29-32]、联合(Combined)积分不等式[33]、Wirtinger-based二重积分不等式[34]、Abel lemma-based不等式[35]等.通过深入研究发现,这些不等式虽然各自基于不同的角度提出,证明过程也是多种多样,但它们之间存在紧密的内在关联性,并且可以纳入到同一个积分/求和不等式理论框架中[27-28].
另一方面,虽然建立起来的不等式对于积分项给出的边界估值越来越精确,但是如果L-K泛函构造不合适,所获得稳定性条件的保守性不会得到明显的降低,甚至不降低[36-37].文[37]已经证明,如果采用简单的L-K泛函(没有进行状态变量扩展),基于Wirtinger-based积分不等式所获得的稳定性条件等价于基于Jensen不等式所获得的稳定性条件,即这两个条件具有相同的保守性.由此可见,构造一个合适的L-K泛函是分析线性时滞系统稳定性的首要任务,是获得松弛稳定性条件的前提条件.传统的L-K泛函一般包含有二次函数项,1重积分项和2重积分项[38-42].当L-K泛函导数中出现1重积分项时,可以采用交叉项技术、自由权矩阵技术或直接采用Jensen不等式进行处理,最终获得具有LMI形式的稳定性条件.为了配合Wirtinger-based积分不等式的使用,文[10]对传统L-K泛函中二次函数项的状态向量进行了增广,扩充了具有状态滞后的状态向量和一重积分项,从而构造了具有增广向量的L-K泛函.
此后,为了配合其它不等式的使用,陆续提出了其它类型的具有增广向量的L-K泛函[43-48].值得一提的是,不同于针对二次函数项进行向量增广,Zhang等在文[36]中提出了一重积分项具有增广向量的L-K泛函.在该L-K泛函中,1重积分项中的被积向量不再是简单的即时状态向量,而是包含了即时状态向量、滞后状态向量、1重积分项和1重积分项等元素的增广向量.由于包含了更多的状态变量信息和时滞变量信息,具有增广向量的L-K1泛函能有效地降低稳定性条件的保守性.除了上述具有增广向量的L-K泛函,最近文献中还提出了其它一些比较新颖的L-K1泛函,如,受到自由权矩阵思想的启发,Lee等在文[49]中构造了称之为Matrix-refined的L-K泛函.该L-K泛函不需要其中的二次函数矩阵P为正定阵,解放了传统L-K泛函对矩阵P必须是正定阵的约束. Zhang等通过对L-K泛函在减小稳定性条件保守性过程中所起的作用进行分析,提出了Delay-product L-K泛函[37].此外,Chen等在文[36]的基础上,提出了积分互补的L-K泛函[50].
总的来说,对于时滞系统(1),为了获得更为松弛的稳定性判别条件,主要从2个方面入手:一是采用边界估值更加精确的积分不等式;二是构造合适的L-K泛函,充分利用系统本身所提供的状态信息和时滞信息.本文将从这两个方面出发回顾近几年线性时滞系统稳定性研究的最新成果,阐述不断发展的L-K泛函方法.
本文所用符号:N代表非负整数集;N+代表正整数集;Rn代表n维实数向量集;Rn×m代表n×m维实矩阵集;Sn代表n×n维实对称矩阵集;S+n代表n×n维实对称正定矩阵集;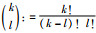
积分不等式是目前控制领域的研究热点之一,国内外许多学者已经投身其中[51-62].引领这场研究热潮的领军人物当数法国学者Seuret. 2013年,他和Gouaisbaut在文[15]中提出了比Jensen不等式更精确的Wirtinger-based积分不等式.而积极推动这场研究热潮的另一位标志性人物是韩国学者Park.他于2015年提出了基于辅助函数的积分不等式[25](Auxiliary-function-based积分不等式).该类不等式不仅包含1重积分不等式,还包含了2重积分不等式,从而拓宽了研究积分不等式的思路.受此思想启发,新的更加精确的1重、2重及多重积分不等式不断地被建立起来.下面我们回顾一下具有代表性的积分不等式.
1.1 1重和2重积分不等式引理1 对于矩阵R∈S+n及可微向量函数x(t):[a,b]→Rn,积分不等式(5)~(7)成立:
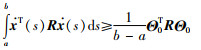
|
(5) |
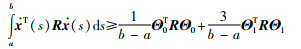
|
(6) |
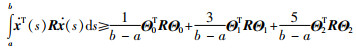
|
(7) |
其中,
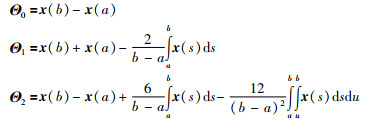
|
由于R为正定矩阵,因而容易看出,Wirtinger-based不等式(6)给出的边界估值精确于Jensen不等式(5)给出的边界估值,而Auxiliary-function-based不等式(7)给出的边界估值精确于Wirtinger-based不等式(6)给出的边界估值.值得注意的是,这3个不等式虽然表现形式上相似,但构造过程却各不相同. Jensen不等式是基于Schur补得到的;Wirtinger-based积分不等式是基于Wirtinger不等式构造出来,证明过程稍显复杂冗长;而Auxiliary-function-based不等式是基于辅助函数(或辅助多项式)建立起来的.
除了1重积分不等式(7),Park等根据辅助函数还建立起了2重积分不等式[25]:
引理2 对于矩阵R∈S+n及可微向量函数x(t):[a,b]→Rn,积分不等式:
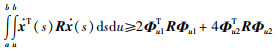
|
(8) |
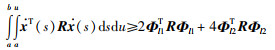
|
(9) |
成立,其中,
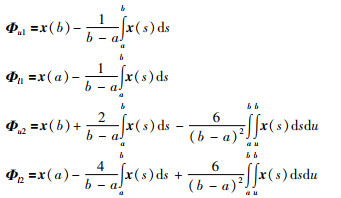
|
当积分重数为两次或两次以上时,积分不等式将出现上积分(如式(8)所示)和下积分(如(9)所示)两种形式.这两种类型的积分不等式可以相互转化.
注1 如果可微向量函数x(t)为定常向量,则积分不等式(5)~(9)的左边等于0.因为不等式(5)~(9)的右边每一个求和项都大于等于0,所以要确保上述不等式成立,每一个求和项必须为0.从而,每个求和项中的向量(如Θ0、Θ1、Φu1等)必须是零向量.可以应用这个简单的规律验证所求积分不等式的准确性.本文后面提到的积分不等式都具有这样的规律.实际上求和不等式同样具有这样的规律.
2015年,Seuret和Gouaisbaut在文[24]中基于Bessel不等式和Legendre多项式建立起了Bessel-Legendre不等式.由于Bessel-Legendre不等式含有一个参变量N,因而其实际上是构成了一个不等式簇.不同的N值,Bessel-Legendre不等式给出不同精度的边界估值.本文在讨论Bessel-Legendre不等式之前,有必要先介绍一下Legendre多项式.假设Lk(s)是k次Legendre多项式,定义为[24]
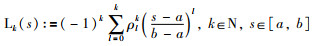
|
(10) |
其中,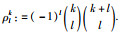
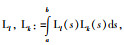
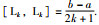
引理3 对于矩阵R∈S+n及可微向量函数x(t):[a,b]→Rn,积分不等式(11)成立:
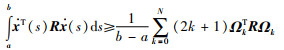
|
(11) |
其中,N∈N,
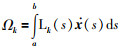
|
从式(11)可以看出,参变量N值越大,Bessel-Legendre不等式给出的边界估值就越精确.可以证明,当N趋向于无穷大时,Bessel-Legendre不等式两边趋于相等[61].由于Bessel-Legendre不等式中包含有Legendre多项式,这就给其应用带来不便.最近出版的文[62]中将Bessel-Legendre不等式进行了改进,实现了去多项式化,即任给一个参变量值,可以直接得到不等式的具体形式.
在建立改进的Bessel-Legendre不等式之前,定义符号:
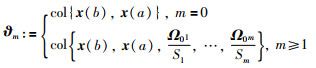
|
(12) |
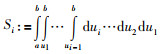
|
(13) |
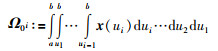
|
(14) |
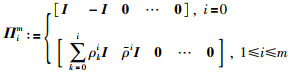
|
(15) |
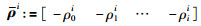
|
(16) |
引理4 对于变量m∈N,矩阵R∈S+n和可微向量函数x(t):[a,b]→Rn,不等式(17)成立:
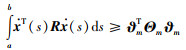
|
(17) |
其中,ϑm定义见式(12),
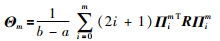
|
改进的Bessel-Legendre不等式已经完全消除了Legendre多项式,其中Πim∈Rn×(m+2)n可根据式(15)计算得到.当m=0时,从式(17)可以直接得到Jensen不等式(5);当m=1时,可以直接得到Wirtinger-based不等式(6);当m=2时,可以直接得到Auxiliary-function-based不等式(7).更多细节读者可以参看文[62].
不难看出,改进的Bessel-Legendre不等式将前面所介绍的Jensen、Wirtinger-based和Auxiliary-function-based等不等式都纳入到了同一个积分不等式理论框架下,并且将其证明过程进行了统一.在建立Bessel-Legendre不等式过程中,Legendre多项式起着关键性的作用.这里需要指出的是,Legendre多项式只是满足内积定义[Ll,Lk]:= 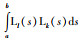
借用建立Bessel-Legendre不等式的思想,文[28]将正交多项式的概念从1重积分内积空间扩展到多重积分内积空间,并在多重积分内积空间中基于正交多项式建立起多重积分不等式簇.在介绍多重积分不等式簇前,首先定义2个符号:
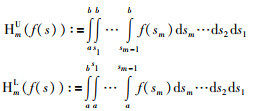
|
如果不特别标出上标,Hm(f(s))指代HmU(f(s))或HmL(f(s)).
引理5 对于变量N∈N,m∈N+,矩阵R∈S+n和可微向量函数x(t):[a, b]→Rn,不等式(18)成立:
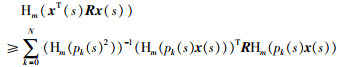
|
(18) |
其中,pk(s)为k次多项式,满足:
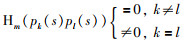
|
需要指出的是,该多重积分不等式簇(18)具有一般性.当Hm(·)指代HmU(·)时,式(18)就是多重上积分不等式簇;当Hm(·)指代HmL(·)时,式(18)就是多重下积分不等式簇.实际上,基于式(18),可以得到任意重数任意精度的积分不等式.目前文献中所建立的1重或多重积分不等式均可纳入到该积分不等式簇的理论框架中.在式(18)中,变量m代表积分的重数,变量N代表所用多项式pk(s)的个数.这里,多项式pk(s)(k∈{0,1,…,N})构成m重积分内积空间中的一组正交基.当m为1,pk(s)为Legendre多项式时,式(18)就变成Bessel-Legendre不等式.更多细节,可以参考文[27-28].
此外,人们在研究时滞系统指数稳定性时通常会在所构造的L-K泛函中加入2重指数加权积分项:
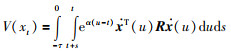
|
这样,L-K泛函的导数中就会出现1重指数加权积分项:
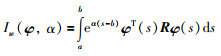
|
如何处理上述1重指数加权积分项,就成为获取具有较小保守性的指数稳定性条件的关键.文[63]基于Schur补和多项式技术建立起了指数加权积分不等式.实际上文[63]中所建立起的1重或2重指数加权积分不等式都可以纳入到上述不等式理论框架中[27-28].进一步地,应用上述建立1重或多重积分不等式簇的思想,同样可以建立起1重或多重指数加权积分不等式簇.
注2 以上讨论的积分不等式除了包含正定阵R外,不包含任何其它额外的自由变量.因此,本文将其归为一类,统称为不含有自由变量的积分不等式.
1.3 含有自由变量的积分不等式如果在前面介绍的积分不等式中引入自由变量,将得到另一种类型的积分不等式:含有自由变量的积分不等式.与不含有自由变量的不等式相比,这类不等式具有不一样的结构形式:积分区间的差值出现在边界估值的分子上.这种优良的结构形式便于人们应用凸性质求解稳定性条件.
最为人们熟知的含有自由变量的积分不等式是2015年Zeng等在文[29]中提出了Free-matrix-based积分不等式,如引理6所示:
引理6 假设矩阵R∈S+n,Z00,Z11∈S3n,Z01∈R3n×3n和N0,N1∈R3n×n满足:
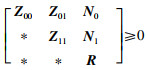
|
(19) |
则对于可微向量函数x(s):[a,b]→Rn,不等式(20)成立:
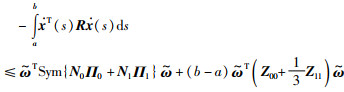
|
(20) |
其中,
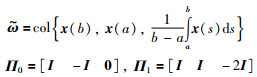
|
如果令Zij=NiR-1NjT,i,j∈{0,1},则根据Schur补,约束不等式(19)必然成立.再令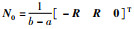
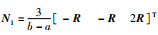
引理7 对于矩阵R∈S+n,M1,M2∈Rn×n和可微向量函数x(s):[a,b]→Rn,不等式(21)成立:
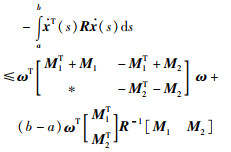
|
(21) |
其中,ω=col{x(b),x(a)}.
可以证明,含有自由变量的Jensen不等式(21)和Jensen不等式(5)具有相同的保守性,即这两个不等式给出了相同精度的边界估值[65].同样可以证明,Wirtinger-based不等式(6)和带有自由变量的Wirtinger-based不等式(20)具有相同的保守性[66].然后需要指出的是,虽然这两类积分不等式具有相同的保守性,但由于它们具有不同的结构形式,导致根据它们所获得的稳定性条件具有不一样的保守性[32-33].在不含有自由变量的积分不等式中,积分区间的差值存在于边界估值的分母中,所以在应用它们进行时滞系统稳定性分析时,通常需要结合矩阵不等式一起使用.另一方面,在含有自由变量的积分不等式中,积分区间的差值存在于边界估值的分子中,此时不再需要使用矩阵不等式,可以直接利用凸性质获得具有LMI形式的稳定性条件.
上述含有自由变量的Jensen不等式(21)和含有自由变量的Wirtinger-based不等式(20)实际上引入了过多的自由变量.这些自由变量去除后,不等式的结构形式不会发生本质的变化.下面介绍含有自由变量的Bessel-Legendre不等式[62]:
引理8 对于变量m∈N,矩阵R∈S+n,Mi∈R(m+2)n×n,i∈{0,1,…,m}和可微向量函数x(s):[a,b]→Rn,不等式(22)成立:
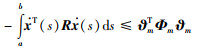
|
(22) |
其中,ϑm和Πim定义见式(12)和式(15),
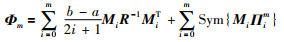
|
当m=0时,可以从式(22)得到改进的含有自由变量的Jensen不等式;当m=1时,可以得到改进的含有自由变量的Wirtinger-based不等式;当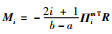
在研究时滞系统(1)稳定性的时候,通常会将积分项δ(t)的积分区间[t,t-hM]一分为二,然后再应用积分不等式进行缩放,具体为
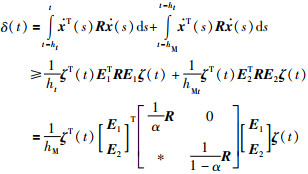
|
(23) |
其中,
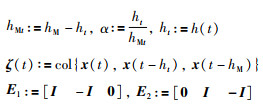
|
从式(23)可以看出,在用Jensen不等式处理后边界的分母中出现了积分区间的差值,这给建立具有LMI形式的稳定性条件带来了困难.这种情况下,通常需要采用矩阵不等式对边界进行进一步的缩放处理. Park等对上述问题进行了研究,于2011年提出了Reciprocally Convex Lemma(RCL).本文给出RCL的矩阵形式[67]:
引理9 假设矩阵R∈S+n和X∈Rn×n满足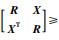
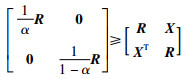
|
(24) |
其中,α∈(0,1).
矩阵不等式(24)形式简洁,应用广泛.由于其给出的边界估值与α完全无关,即无论α取何值,其边界估值都是相同的,这必然会导致该矩阵不等式具有较大的保守性.最近Zhang等对RCL进行了改进,提出了α相关的矩阵不等式[33, 36].
引理10 对于矩阵R∈S+n和X∈Rn×n,矩阵不等式(25)成立:
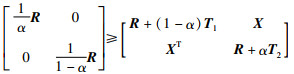
|
(25) |
其中,α∈(0,1),T1=R-XR-1XT,T2=R-XTR-1X.
α相关的矩阵不等式(25)不再受到矩阵不等式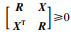
引理11 对于矩阵R∈S+n和X1,X2∈Rn×n,矩阵不等式(26)成立:
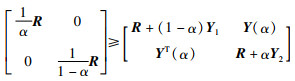
|
(26) |
其中,α∈(0,1),Y1=R-X1R-1X1T,Y2=R-X2TR-1X2和Y(α)=αX1+(1-α)X2.
不难验证,当X1=X2=X时式(26)退化为式(25).
3 基于L-K泛函方法的稳定性条件 3.1 简单的L-K泛函早期人们在研究时变时滞系统(1)稳定性时常采用简单L-K泛函[1-3]:
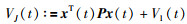
|
(27) |
其中,V1(t)定义在式(3),P为正定阵.基于L-K泛函(27)并应用Jensen不等式(5)和矩阵不等式(24),可以得到定理1所示的稳定性条件[1, 69-70]:
定理1 假设给定标量hM,dm和dM满足式(2),对于矩阵P,Q1,Q2,R∈S+n和X∈Rn×n,时滞系统(1)是渐近稳定的,如果式(28)、式(29)的LMIs成立:
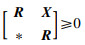
|
(28) |
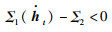
|
(29) |
其中,
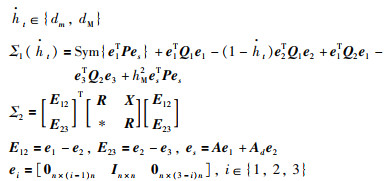
|
注3 在建立定理1的过程中,应用了一元一次凸性质,即对于任意z∈[zm,zM],不等式:
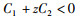
|
成立,当且仅当C1+zmC2 < 0和C1+zMC2 < 0成立,其中,C1和C2为与z无关的标量.
3.2 具有增广向量的L-K泛函为了配合Wirtinger-based不等式的使用,文[15]构造了具有增广向量的L-K泛函:
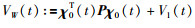
|
(30) |
其中,
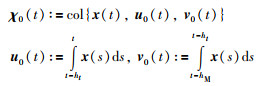
|
基于L-K泛函(30)并应用Wirtinger-based不等式(6)和矩阵不等式(24),可以得到如定理2所示的稳定性条件[15].
定理2 假设给定的标量hM,dm和dM满足式(2).对于矩阵P∈S+3n,Q1,Q2,R∈S+n和X∈R2n×2n,时滞系统(1)是渐近稳定的,如果式(31)的LMIs成立:
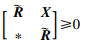
|
(31) |
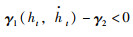
|
(32) |
其中,
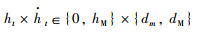
|
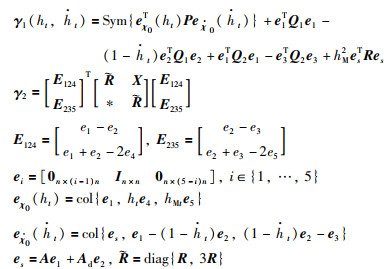
|
在建立定理2的过程中,应用了二元一次凸性质.需要指出的是,如果采用简单L-K泛函(27),基于Wirtinger-based不等式得到的稳定性条件将与基于Jensen不等式得到的稳定性条件具有相同的保守性.因此,如何构造合适的L-K泛函从而最大限度地利用Wirtinger-based不等式或其它更高精度的积分不等式,是值得研究的课题.
文[36-37, 71]深入研究了L-K泛函在减小稳定性条件保守性方面的作用,提出了在配合积分不等式应用时如何构造L-K泛函的方法.本文以L-K泛函(27)、(30)举例,说明其基本思想.在应用Wirtinger-based不等式缩放积分项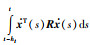
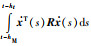
基于这一思想,如果采用Bessel-Legendre不等式时构造L-K泛函:
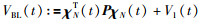
|
(33) |
其中,
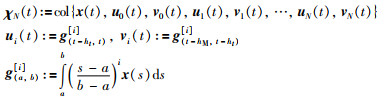
|
本文将获得一个含有参变量N的稳定性条件簇.该稳定性条件簇将包含定理1和定理2,而且随着参变量N值的增加,稳定性条件的保守性将不断降低.有兴趣的读者可以自行推导.
除了上述扩展二次函数项外,最近文[15]提出了构建增广向量L-K泛函新的思想,即扩展1重积分项.其所构造的L-K泛函为
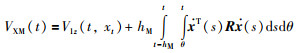
|
(34) |
其中,
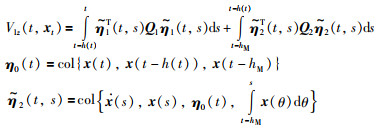
|
L-K泛函(34)没有包含二次函数项,只包含了1重积分项和2重积分项.其中1重积分项的状态向量进行了大幅度地扩展,加入了状态向量的导数项,滞后项和1重积分项等.这样,相关状态向量之间的关系可以通过正定阵Q1和Q2紧密地耦合在一起,有效地降低了所得稳定性条件的保守性.后来,Chen等基于文[15]中提出的思想对L-K泛函(34)进行了进一步改进,在增广向量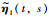
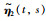
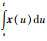
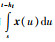
注3 当对L-K泛函(34)求导时,会出现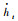
引理12 对于一元二次函数f(x)=a2x2+a1x+a0,其中a2,a1,a0∈R,不等式f(x) < 0成立,∀x∈[0,h],如果f(0) < 0,f(h) < 0,-a2h2+f(0) < 0.
当a2 < 0时,引理12给出的条件具有一定的保守性.最近Chen等通过对区间[0,h]进行平均分割,提出了保守性更小的结论[74]:
引理13 对于一元二次函数f(x)=a2x2+a1x+a0,其中a2,a1,a0∈R,如果不等式:
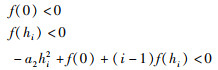
|
成立,则不等式f(x) < 0成立,∀x∈[0,h],其中,i∈{1,…,N},N∈N+,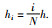
为了确保L-K泛函(27)是正定的,通常情况下都是要求矩阵P、Q1、Q2和R是正定矩阵.然而,在文[75-76]中Xu等提出了非常新颖的思想,松绑了所有矩阵必须是正定阵的约束条件,其基本结论为:对于矩阵P,Q2,R∈S+n和Q1∈Sn,如果不等式:
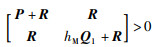
|
成立,则L-K泛函(27)是正定的.这样的条件弱化了对矩阵Q1的限制,有利于降低稳定性条件的保守性.另外,Lee等在文[72]中基于构造Free-matrix-based不等式的思想,提出了另一种结构新颖的L-K泛函.其基本结论为:
引理14 对于标量τ1,τ2,τ3满足τ1≤τ2和τ2-τ1≤τ3,可微向量函数x(s):[τ1,τ2]→Rn,矩阵D4∈S+3n,D1∈S3n,D6∈Sn,D2∈R3n×3n,D3,D5∈R3n×n,满足不等式:
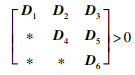
|
则式(35)的泛函是正定的:
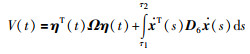
|
(35) |
其中,
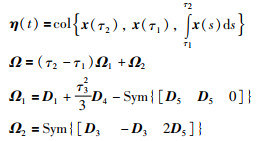
|
引理14构造L-K泛函的方法隐含着一个重要的思想,即可以通过积分不等式来构造新的L-K泛函,这极大地拓宽了构造L-K泛函的思路[77-80].比如,基于这一思想,Lee等人在文[78]中应用Jensen不等式构建了L-K泛函:
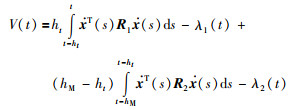
|
(36) |
其中,
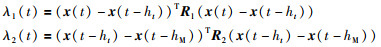
|
与常规的L-K泛函不同,在L-K泛函(36)中除了两个积分项外还引入了负的二次函数项λ1(t)和λ2(t).负项的引入,有利于减小所得稳定性条件的保守性.
在深入研究了L-K泛函在降低稳定性条件保守性作用的情况下,Zhang等在文[37]中提出了Delay-product-type类型的L-K泛函,即在传统的L-K泛函中,加入了2个带有时滞变量乘积的二次函数项:
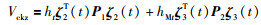
|
(37) |
其中,
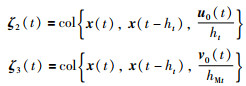
|
另外,为了充分利用2重或多重积分不等式,目前一些文献中构造的L-K泛函不仅包含1重和2重积分项,还包含3重或多重积分项[51, 60, 81-85].此外,采用时滞变量分割的方法构造L-K泛函,也是目前人们常用的方法.更多细节读者可以参考文[86].
4 总结与展望至此,本文回顾了线性时滞系统稳定性研究的最新成果,讨论了L-K泛函方法在时滞系统稳定性研究中的应用,重现了近几年积分不等式的发展历程,重点分析并比较了几个具有代表性的积分不等式.同时,本文也回顾了最近几年来发展起来的具有代表性的L-K泛函,重点分析了在结合积分不等式的应用过程中如何构造合适的L-K泛函.
虽然基于不等式的L-K泛函方法发展迅速,在时滞系统稳定性研究中取得了丰硕的成果,然而仍有一些具有挑战性的问题需要解决:
1) 目前应用基于不等式的L-K泛函方法研究时变时滞系统的稳定性,获得的基本上都是充分条件,而非充分必要条件.虽然计算得到的结果越来越接近于分析值,但如何获得充分必要条件,仍然是一个充满挑战的开放性问题.
2) 评价一个稳定性条件好坏的指标通常有2个:一个是保守性,一个是计算量. “好”的稳定性条件是在计算量增加不多的情况下不断降低保守性,或是保守性维持不变的情况下减小计算量.如果构造一个合适的L-K泛函,从而获得“好”的稳定性条件,是一个值得深入的研究课题.
3) 目前文献中提出了多种多样的L-K泛函.不同的L-K泛函,要么可以获得更小的保守性,要么引入较少的变量.然后目前还没有一种大家公认的L-K泛函,在减小稳定性条件保守性和计算量之间取得最佳平衡.
4) 网络系统、脉冲系统和采样系统等都可以建模成时滞系统进行研究.如何将基于不等式的L-K泛函方法应用于这些系统的稳定性分析中值得以后进一步研究.
| [1] | Gu K, Kharitonov V L, Chen J. Stability of time-delay systems[M]. Berlin, Germany: Springer-Verlag, 2003. |
| [2] | Richard J P. Time-delay systems:An overview of some recent advances and open problems[J]. Automatica, 2003, 39(10): 1667–1694. DOI:10.1016/S0005-1098(03)00167-5 |
| [3] | Fridman E. Introduction to time-delay systems:Analysis and control[M]. Berlin, Germany: Springer-Verlag, 2014. |
| [4] | Li X, Gao H. A new model transformation of discrete-time systems with time-varying delay and its application to stability analysis[J]. IEEE Transactions on Automatic Control, 2011, 56(9): 2172–2178. DOI:10.1109/TAC.2011.2146850 |
| [5] | Shao H, Han Q L. New stability criteria for linear discrete-time systems with interval-like time-varying delays[J]. IEEE Transactions on Automatic Control, 2011, 56(3): 619–625. DOI:10.1109/TAC.2010.2095591 |
| [6] | Kao C Y, Rantzer A. Stability analysis of systems with uncertain time-varying delays[J]. Automatica, 2007, 43(6): 959–970. DOI:10.1016/j.automatica.2006.12.006 |
| [7] | Megretski A, Rantzer A. System analysis via integral quadratic constraints[J]. IEEE Transactions on Automatic Control, 1997, 42(6): 819–830. DOI:10.1109/9.587335 |
| [8] | Ma Q, Gu K, Choubedar N. Strong stability of a class of difference equations of continuous time and structured singular value problem[J]. Automatica, 2018, 87: 32–39. DOI:10.1016/j.automatica.2017.09.012 |
| [9] | Zhou B, Egorov A V. Razumikhin and Krasovskii stability theorems for time-varying time-delay systems[J]. Automatica, 2016, 71: 281–291. DOI:10.1016/j.automatica.2016.04.048 |
| [10] | Moon Y S, Park P, Kwon W H, et al. Delay-dependent robust stabilization of uncertain state-delayed systems[J]. International Journal of Control, 2001, 74(14): 1447–1455. DOI:10.1080/00207170110067116 |
| [11] | Fridman E, Shaked U. A descriptor system approach to H∞ control of linear time-delay systems[J]. IEEE Transactions on Automatic Control, 2002, 47(2): 253–270. DOI:10.1109/9.983353 |
| [12] | He Y, Wang Q G, Xie L, et al. Further improvement of free-weighting matrices technique for systems with time-varying delay[J]. IEEE Transactions on Automatic Control, 2007, 52(2): 293–299. DOI:10.1109/TAC.2006.887907 |
| [13] | Kim J H. Further improvement of Jensen inequality and application to stability of time-delayed systems[J]. Automatica, 2016, 64: 121–125. DOI:10.1016/j.automatica.2015.08.025 |
| [14] | Liu K, Seuret A, Xia Y. Stability analysis of systems with time-varying delays via the second-order Bessel-Legendre inequality[J]. Automatica, 2017, 76: 138–142. DOI:10.1016/j.automatica.2016.11.001 |
| [15] | Seuret A, Gouaisbaut F. Wirtinger-based integral inequality:Application to time-delay systems[J]. Automatica, 2013, 49: 2860–2866. DOI:10.1016/j.automatica.2013.05.030 |
| [16] | Park P G. A delay-dependent stability criterion for systems with uncertain time-invariant delays[J]. IEEE Transactions on Automatic Control, 1999, 44(4): 876–877. DOI:10.1109/9.754838 |
| [17] | Fridman E. New Lyapunov-Krasovskii functionals for stability of linear retarded and neutral type systems[J]. Systems & Control Letters, 2001, 43(4): 309–319. |
| [18] | He Y, Wu M, She J H, et al. Delay-dependent robust stability criteria for uncertain neutral systems with mixed delays[J]. Systems & Control Letters, 2004, 51(1): 57–65. |
| [19] | He Y, Wu M, She J H, et al. Parameter-dependent Lyapunov functional for stability of time-delay systems with polytopic-type uncertainties[J]. IEEE Transactions on Automatic Control, 2004, 49(5): 828–832. DOI:10.1109/TAC.2004.828317 |
| [20] | Xu S, Lam J, Zou Y. Simplified descriptor system approach to delay-dependent stability and performance analyses for time-delay systems[J]. IEE Proceedings-Control Theory and Applications, 2005, 152(2): 147–151. DOI:10.1049/ip-cta:20045023 |
| [21] | Xu S, Lam J. A survey of linear matrix inequality techniques in stability analysis of delay systems[J]. International Journal of Systems Science, 2008, 39(12): 1095–1113. DOI:10.1080/00207720802300370 |
| [22] | Briat C. Convergence and equivalence results for the Jensen's inequality-Application to time-delay and sampled-data systems[J]. IEEE Transactions on Automatic Control, 2011, 56(7): 1660–1665. DOI:10.1109/TAC.2011.2121410 |
| [23] | Seuret A, Gouaisbaut F, Fridman E. Stability of discrete-time systems with time-varying delays via a novel summation inequality[J]. IEEE Transactions on Automatic Control, 2015, 60(10): 2740–2745. DOI:10.1109/TAC.2015.2398885 |
| [24] | Seuret A, Gouaisbaut F. Hierarchy of LMI conditions for the stability analysis of time-delay systems[J]. Systems & Control Letters, 2015, 81: 1–7. |
| [25] | Park P G, Lee W I, Lee S Y. Auxiliary function-based integral inequalities for quadratic functions and their applications to time-delay systems[J]. Journal of the Franklin Institute, 2015, 352(4): 1378–1396. DOI:10.1016/j.jfranklin.2015.01.004 |
| [26] | Nam P T, Trinh H, Pathirana P N. Discrete inequalities based on multiple auxiliary functions and their applications to stability analysis of time-delay systems[J]. Journal of the Franklin Institute, 2015, 352(12): 5810–5831. DOI:10.1016/j.jfranklin.2015.09.018 |
| [27] | Chen J, Xu S, Ma Q, et al. Two novel general summation inequalities to discrete-time systems with time-varying delay[J]. Journal of the Franklin Institute, 2017, 354(13): 5537–5558. DOI:10.1016/j.jfranklin.2017.06.008 |
| [28] | Chen J, Xu S, Chen W, et al. Two general integral inequalities and their applications to stability analysis for systems with time-varying delay[J]. International Journal of Robust and Nonlinear Control, 2016, 26(18): 4088–4103. DOI:10.1002/rnc.3551 |
| [29] | Zeng H B, He Y, Wu M, et al. Free-matrix-based integral inequality for stability analysis of systems with time-varying delay[J]. IEEE Transactions on Automatic Control, 2015, 60(10): 2768–2772. DOI:10.1109/TAC.2015.2404271 |
| [30] | Chen J, Xu S, Zhang B. Single/multiple integral inequalities with applications to stability analysis of time-delay systems[J]. IEEE Transactions on Automatic Control, 2017, 62(7): 3488–3493. DOI:10.1109/TAC.2016.2617739 |
| [31] | Chen J, Xu S, Jia X, et al. Novel summation inequalities and their applications to stability analysis for systems with time-varying delay[J]. IEEE Transactions on Automatic Control, 2017, 62(5): 2470–2475. DOI:10.1109/TAC.2016.2606902 |
| [32] | Chen J, Lu J, Xu S. Summation inequality and its application to stability analysis for time-delay systems[J]. IET Control Theory & Applications, 2016, 10(4): 391–395. |
| [33] | Zhang C K, He Y, Jiang L, et al. An improved summation inequality to discrete-time systems with time-varying delay[J]. Automatica, 2016, 74: 10–15. DOI:10.1016/j.automatica.2016.07.040 |
| [34] | Park M J, Kwon O M, Park J H, et al. Stability of time-delay systems via Wirtinger-based double integral inequality[J]. Automatica, 2015, 55: 204–208. DOI:10.1016/j.automatica.2015.03.010 |
| [35] | Zhang X M, Han Q L. Abel lemma-based finite-sum inequality and its application to stability analysis for linear discrete time-delay systems[J]. Automatica, 2015, 57: 199–202. DOI:10.1016/j.automatica.2015.04.019 |
| [36] | Zhang X M, Han Q L, Seuret A, et al. An improved reciprocally convex inequality and an augmented Lyapunov-Krasovskii functional for stability of linear systems with time-varying delay[J]. Automatica, 2017, 84: 221–226. DOI:10.1016/j.automatica.2017.04.048 |
| [37] | Zhang C K, He Y, Jiang L, et al. Notes on stability of time-delay systems:Bounding inequalities and augmented Lyapunov-Krasovskiifunctionals[J]. IEEE Transactions on Automatic Control, 2016, 62(10): 5331–5336. |
| [38] | Han Q L. Absolute stability of time-delay systems with sector-bounded nonlinearity[J]. Automatica, 2005, 41(12): 2171–2176. DOI:10.1016/j.automatica.2005.08.005 |
| [39] | Zhang B, Xu S, Zou Y. Improved stability criterion and its applications in delayed controller design for discrete-time systems[J]. Automatica, 2008, 44(11): 2963–2967. DOI:10.1016/j.automatica.2008.04.017 |
| [40] | Shao H. New delay-dependent stability criteria for systems with interval delay[J]. Automatica, 2009, 45(3): 744–749. DOI:10.1016/j.automatica.2008.09.010 |
| [41] | Xu S, Lam J. On equivalence and efficiency of certain stability criteria for time-delay systems[J]. IEEE Transactions on Automatic Control, 2007, 52(1): 95–101. DOI:10.1109/TAC.2006.886495 |
| [42] | Xu S, Lam J. Improved delay-dependent stability criteria for time-delay systems[J]. IEEE Transactions on Automatic Control, 2005, 50(3): 384–387. DOI:10.1109/TAC.2005.843873 |
| [43] | He Y, Wang Q G, Lin C, et al. Augmented Lyapunov functional and delay-dependent stability criteria for neutral systems[J]. International Journal of Robust and Nonlinear Control:IFAC-Affiliated Journal, 2005, 15(18): 923–933. DOI:10.1002/rnc.1039 |
| [44] | Lin C, Wang Q G, Lee T H. A less conservative robust stability test for linear uncertain time-delay systems[J]. IEEE Transactions on Automatic Control, 2006, 51(1): 87–91. DOI:10.1109/TAC.2005.861720 |
| [45] | Kwon O M, Park M J, Park J H, et al. Improved results on stability of linear systems with time-varying delays via Wirtinger-based integral inequality[J]. Journal of the Franklin Institute, 2014, 351(12): 5386–5398. DOI:10.1016/j.jfranklin.2014.09.021 |
| [46] | Zhang X M, Han Q L, Zeng Z. Hierarchical type stability criteria for delayed neural networks via canonical Bessel-Legendre inequalities[J]. IEEE Transactions on Cybernetics, 2017, 48(5): 1660–1671. |
| [47] | Sun J, Liu G P, Chen J, et al. Improved delay-range-dependent stability criteria for linear systems with time-varying delays[J]. Automatica, 2010, 46(2): 466–470. DOI:10.1016/j.automatica.2009.11.002 |
| [48] | Sun J, Han Q L, Chen J, et al. Less conservative stability criteria for linear systems with interval time-varying delays[J]. International Journal of Robust and Nonlinear Control, 2015, 25(4): 475–485. DOI:10.1002/rnc.3096 |
| [49] | Lee T H, Park J H, Xu S. Relaxed conditions for stability of time-varying delay systems[J]. Automatica, 2017, 75: 11–15. DOI:10.1016/j.automatica.2016.08.011 |
| [50] | Chen J, Park J H, Xu S. Stability analysis of continuous-time systems with time-varying delay using new Lyapunov-Krasovskii functionals[J]. Journal of the Franklin Institute, 2018, 355(13): 5957–5967. DOI:10.1016/j.jfranklin.2018.05.054 |
| [51] | Gyurkovics E, Takacs T. Multiple integral inequalities and stability analysis of time delay systems[J]. Systems & Control Letters, 2016, 96: 72–80. |
| [52] | Liu K, Seuret A. Comparison of bounding methods for stability analysis of systems with time-varying delays[J]. Journal of the Franklin Institute, 2017, 354: 2979–2993. DOI:10.1016/j.jfranklin.2017.02.007 |
| [53] | Trinh H. Refined Jensen-based inequality approach to stability analysis of time-delay systems[J]. IET Control Theory & Applications, 2015, 9(14): 2188–2194. |
| [54] | Liu X, Wang F, Tang M. Auxiliary function-based summation inequalities and their applications to discrete-time systems[J]. Automatica, 2017, 78: 211–215. DOI:10.1016/j.automatica.2016.12.036 |
| [55] | Gyurkovics E, Szabo-Varga G, Kiss K. Stability analysis of linear systems with interval time-varying delays utilizing multiple integral inequalities[J]. Applied Mathematics and Computation, 2017, 311: 164–177. DOI:10.1016/j.amc.2017.05.004 |
| [56] | Han Q L. A discrete delay decomposition approach to stability of linear retarded and neutral systems[J]. Automatica, 2009, 45(2): 517–524. DOI:10.1016/j.automatica.2008.08.005 |
| [57] | Gyurkovics E, Takacs T. Comparison of some bounding inequalities applied in stability analysis of time-delay systems[J]. Systems & Control Letters, 2019, 123: 40–46. |
| [58] | Lee S Y, Lee W I, Park P G. Polynomials-based integral inequality for stability analysis of linear systems with time-varying delays[J]. Journal of the Franklin Institute, 2017, 354(4): 2053–2067. DOI:10.1016/j.jfranklin.2016.12.025 |
| [59] | Zhang C K, He Y, Jiang L, et al. Delay-dependent stability analysis of neural networks with time-varying delay:A generalized free-weighting-matrix approach[J]. Applied mathematics and computation, 2017, 294: 102–120. DOI:10.1016/j.amc.2016.08.043 |
| [60] | Wang J, Wang Z, Ding S, et al. Refined Jensen-based multiple integral inequality and its application to stability of time-delay systems[J]. IEEE/CAA Journal of Automatica Sinica, 2018, 5(3): 758–764. DOI:10.1109/JAS.2018.7511087 |
| [61] | Seuret A, Gouaisbaut F. Stability of linear systems with time-varying delays using Bessel-Legendre inequalities[J]. IEEE Transactions on Automatic Control, 2017, 63(1): 225–232. |
| [62] | Chen J, Park J H, Xu S. Stability analysis for delayed neural networks with an improved general free-matrix-based integral inequality[J/OL]. IEEE Transactions on Neural Networks and Learning Systems, DOI: 10.1109/TNNLS.2019.2909350.(2019-04-26)[2019-06-15].https://ieeexplore.ieee.org/document/8700596. |
| [63] | Trinh H. Exponential stability of time-delay systems via new weighted integral inequalities[J]. Applied Mathematics and Computation, 2016, 275: 335–344. DOI:10.1016/j.amc.2015.11.076 |
| [64] | Zhang X M, Wu M, She J H, et al. Delay-dependent stabilization of linear systems with time-varying state and input delays[J]. Automatica, 2005, 41(8): 1405–1412. DOI:10.1016/j.automatica.2005.03.009 |
| [65] | Ji X, Su H. A note on equivalence between two integral inequalities for time-delay systems[J]. Automatica, 2015, 53: 244–246. DOI:10.1016/j.automatica.2014.12.030 |
| [66] | Gyurkovics E. A note on Wirtinger-type integral inequalities for time-delay systems[J]. Automatica, 2015, 61: 44–46. DOI:10.1016/j.automatica.2015.07.033 |
| [67] | Park P G, Ko J W, Jeong C. Reciprocally convex approach to stability of systems with time-varying delays[J]. Automatica, 2011, 47(1): 235–238. DOI:10.1016/j.automatica.2010.10.014 |
| [68] | Seuret A, Gouaisbaut F. Delay-dependent reciprocally convex combination lemma[J/OL]. Rapport LAAS n16006, 2016.(2016-11-11)[2019-06-15]. https://hal.archives-ouvertes.fr/hal-01257670. |
| [69] | Ariba Y, Gouaisbaut F. An augmented model for robust stability analysis of time-varying delay systems[J]. International Journal of Control, 2009, 82(9): 1616–1626. DOI:10.1080/00207170802635476 |
| [70] | Xiao S P, Lian H, Zeng H, et al. Analysis on robust passivity of uncertain neural networks with time-varying delays via free-matrix-based integral inequality[J]. International Journal of Control Automation and Systems, 2017, 15(5): 2385–2394. DOI:10.1007/s12555-016-0315-0 |
| [71] | Zhang X M, Han Q L, Seuret A, et al. Overview of recent advances in stability of linear systems with time-varying delays[J]. IET Control Theory & Applications, 2018, 13(1): 1–16. |
| [72] | Lee T H, Park J H. A novel Lyapunov functional for stability of time-varying delay systems via matrix-refined-function[J]. Automatica, 2017, 80: 239–242. DOI:10.1016/j.automatica.2017.02.004 |
| [73] | Yang F, He J, Kang P, et al. Delay rangeandrate dependent stability criteria for systems with interval time-varying delay via a quasi-quadratic convex framework[J]. International Journal of Robust and NonlinearControl, 2019, 29(8): 2494–2509. DOI:10.1002/rnc.4505 |
| [74] | Chen J, Park J H, Xu S. Stability analysis of systems with time-varying delay:A quadratic-partitioning method[J]. IET Control Theory & Applications, 2019, 13(18): 3184–3189. |
| [75] | Xu S, Lam J, Zhang B, et al. New insight into delay-dependent stability of time-delay systems[J]. International Journal of Robust and Nonlinear Control, 2015, 25(7): 961–970. DOI:10.1002/rnc.3120 |
| [76] | Xu S, Lam J, Zhang B, et al. A new result on the delay-dependent stability of discrete systems with time-varying delays[J]. International Journal of Robust and Nonlinear Control, 2014, 24(16): 2512–2521. DOI:10.1002/rnc.3006 |
| [77] | Li Z, Yan H, Zhang H, et al. Improved inequality-based functions approach for stability analysis of time delay system[J]. Automatica, 2019, 108: 108416. DOI:10.1016/j.automatica.2019.05.033 |
| [78] | Lee T H, Park J H. Improved stability conditions of time-varying delay systems based on new Lyapunov functionals[J]. Journal of the Franklin Institute, 2018, 355(3): 1176–1191. DOI:10.1016/j.jfranklin.2017.12.014 |
| [79] | Xu H T, Zhang C K, Jiang L, et al. Stability analysis of linear systems with two additive time-varying delays via delay-product-type Lyapunov functional[J]. Applied Mathematical Modelling, 2017, 45: 955–964. DOI:10.1016/j.apm.2017.01.032 |
| [80] | Li Z, Huang C, Yan H. Stability analysis for systems with time delays via new integral inequalities[J]. IEEE Transactions on Systems, Man, and Cybernetics:Systems, 2017, 48(12): 2495–2501. |
| [81] | Kim J H. Note on stability of linear systems with time-varying delay[J]. Automatica, 2011, 47(9): 2118–2121. DOI:10.1016/j.automatica.2011.05.023 |
| [82] | Jiang X, Han Q L. Delay-dependent robust stability for uncertain linear systems with interval time-varying delay[J]. Automatica, 2006, 42(6): 1059–1065. DOI:10.1016/j.automatica.2006.02.019 |
| [83] | Zhang X M, Han Q L. Novel delay-derivative-dependent stability criteria using new bounding techniques[J]. International Journal of Robust and Nonlinear Control, 2013, 23(13): 1419–1432. DOI:10.1002/rnc.2829 |
| [84] | Yue D, Tian E, Zhang Y. A piecewise analysis method to stability analysis of linear continuous/discrete systems with time-varying delay[J]. International Journal of Robust and Nonlinear Control:IFAC-Affiliated Journal, 2009, 19(13): 1493–1518. DOI:10.1002/rnc.1399 |
| [85] | Chen J, Park J H, Xu S. Stability analysis for neural networks with time-varying delay via improved techniques[J]. IEEE Transactions on Cybernetics, 2019, 49(12): 4495–4500. DOI:10.1109/TCYB.2018.2868136 |
| [86] | Park J H, Lee T H, Liu Y, et al. Dynamic systems with time delays:Stability and control[M]. Singapore: Springer-Nature, 2019. |



