2. 浙江警察学院公共基础部, 浙江 杭州 310053;
3. 浙江警察学院计算机与信息安全系, 浙江 杭州 310053
2. Basic Courses Department, Zhejiang Police College, Hangzhou 310053, China;
3. Department of Computer and Information Security, Zhejiang Police College, Hangzhou 310053, China
0 引言
迭代学习控制(iterative learning control,ILC)通过在有限区间上重复实验,不断调整控制输入以便减小输出误差,并逐渐达到精确跟踪[1-5].应用迭代学习控制方法时不仅不需要知道系统的精确模型,还能够抑制周期性扰动,所以ILC被应用于工业机器人机械臂控制、化工间歇过程控制、车间流水线控制及电路稳定性控制等场合.但是应用ILC方法时,若要达到完美跟踪必须保证每次迭代时初始状态偏差为0,但这在实际中不可能做到.因此,研究任意初值条件下的迭代学习控制不仅是非常必要的,而且十分有意义.重复学习控制则适用于目标轨迹具有周期性的受控对象.通过利用前一周期的输入输出信息来改善当前的输入信息,以期达到精确跟踪.对受控对象而言,上一周期的终点是下一周期的起点,因此,对于重复学习控制而言,初值问题重要性并不明显.两种学习控制的差别在于迭代学习控制在经过足够多次迭代以后能够达到任意小误差跟踪,而重复控制只能在无限区间上实现渐近跟踪[6].
迭代学习控制的初值问题引起了很多学者的兴趣[7-14].文[7]通过设置边界层,迫使跟踪误差在边界层的限定下渐近收敛至0.文[8]采用吸引子方法首先给出了相应微分方程的解,然后通过不断迭代的方式让系统逐渐逼近该微分方程的解.文[9]利用高阶内模控制方法设计参数学习律,确保系统收敛.文[10]通过改变参考轨迹的方法实现了在指定区间上的精确跟踪,但参考轨迹会因为每次迭代时初态的不同而重新进行设置.文[11]针对任意初态下的非线性离散系统,实现了逐点跟踪.相对于利用李亚普诺夫方法修正初态偏差而言,利用压缩映射方法来解决初态问题进展缓慢.对于具有固定初态的高相对阶多智能体系统,文[12]提出了一种新的误差修正方法——step-by-step修正方法,该方法首先修正最高阶状态偏差,然后是次高阶状态偏差,以此类推,直到所有状态偏差修正操作完成后系统才能达到完全跟踪.针对系统输入增益精确已知的非线性连续系统,文[13]提出了一种修正方法,实现了渐近跟踪.到目前为止,对迭代学习控制而言,采用压缩映射方法来应对任意初态问题仍无有效方案.
自上世纪以来,自适应控制得到了广泛的重视,到目前为止,其作为一个专门的控制方法至少已有60余年.尽管学者们对自适应控制的定义和理解不尽相同,但其基本思想一致,即在对被控对象系统参数未知或了解不多时如何设计控制律使得系统能够根据实际情况自动调节控制律并跟踪上被控对象[14-15].目前自适应控制在石油化工[16]、电力电机系统[17]、航天[18]等方面得到了广泛应用.自上世纪90年代以来,自适应方法陆续应用于迭代学习控制或重复控制中,并取得了较大进展.文[19]在无需知道机械臂确切参数的前提下和李亚普诺夫泛函框架下,利用跟踪速度和位置误差的线性组合调整非线性前馈补偿来进行重复学习控制的学习律设计.文[20]针对不确定机器人系统,设计了反馈和前馈学习律,并证明了误差的收敛.文[21]从自适应控制的角度考虑迭代学习控制问题,首次在迭代学习控制中引入微分自适应学习控制律,并证明了系统误差均方收敛.对于非线性时变可参数化系统.文[22]借助复合能量函数提出了一种新的学习算法,该算法能够使得系统沿迭代轴渐近收敛.文[23]针对大规模不确定系统,利用自适应反推技术,实现了闭环系统的全局稳定.这些文献为自适应方法在迭代学习控制中得到更广泛的应用提供了参考.
虽然在迭代学习控制或重复控制中利用自适应方法的研究成果较丰富,但是在经典自适应控制方法中利用迭代学习控制思想的并不多见,因为在经典自适应中,控制过程并不满足可重复性或周期性.本文针对非线性可参数化系统,借助迭代学习控制的思想,提出了一种新的自适应控制策略.该方法将迭代学习控制中的自适应策略和初态偏差修正方法应用于一般的过程控制中,从本质上说,就是通过不断修正跟踪误差和参数学习来减小跟踪误差.最后,通过数值仿真验证了该方法的有效性.
1 问题阐述考虑非线性系统:
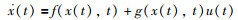
|
(1) |
其中,t∈[0,T];x(t)∈R是状态变量,u(t)∈R是系统的输入变量(前述变量相应可以简写为x,u),并且f(·,·)和g(·,·):R×[0,T]|→R是满足一定条件的未知非线性函数. xd(t)(简写为xd)是给定的期望轨迹.根据期望轨迹,可以定义误差:
e(t)=x(t)-xd(t)
假设1 初始状态x(0)是任意值但不是无限大,也就是说,系统初始误差e(0)可以是任意值但有界,并且状态x(t)是可测的.
假设2 g(x(t),t)≠0并且g(x(t),t)的方向恒定,本文假设g(x(t),t)≻0,而且存在两个函数g1(x(t),t)和g2(x(t),t)满足条件:
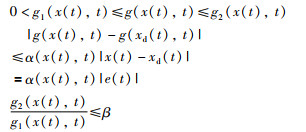
|
为了便于后面的收敛性分析,采用下面的形式来描述系统(1):
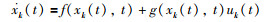
|
(2) |
其中,t是有限时间;k=1,2,…表示第k个过程;xk(t)∈R是状态变量,uk(t)∈R是系统的输入变量(前述变量相应可以简写为xk,uk),fk(·,·)和gk(·,·):R×[0,h)∈R是满足一定条件的未知非线性函数.
对于系统(2),有式(3)成立:
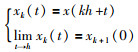
|
(3) |
同理,xk,d(t),fk(·,·),gk(·,·),ek(t)也具有上述性质.
注1 从形式上看,式(3)中的xk(t)及xk,d(t),fk(·,·),gk(·,·),ek(t)似乎满足重复学习的要求,事实上并不满足,因为被跟踪对象的轨迹并不满足周期性,而且该系统也不满足过程可重复的要求,式(3)中的k并不是迭代次数,只是第k个子过程而已.总之,系统(3)的控制过程并不满足重复控制的要求,也不满足学习控制的要求,本文只是将被控过程分成若干个子过程,以便在控制过程中每一个子过程(第1个子过程除外)都可以学习前一子过程的信息而已.在控制过程中进行子过程切分时,必须要求子过程区间长度相等(当然,最后一个除外).
定义1 滤波误差函数:
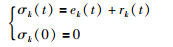
|
(4) |
其中,修正函数rk(t)采用形式:
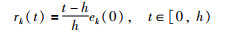
|
为了方便后续设计和分析,引入文[8]中的定义和引理.
定义2 设饱和函数sat(p,p1,p2):
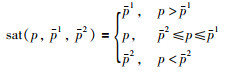
|
其中,p1和p2是相应的上界和下界.
引理1 设a,a*为实变量,并令a*=sat(a,p1,p2),则有:
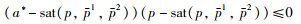
|
证明 当a=p时,易证上面的引理成立.
当a < p时,根据变量a的定义有p2≤a*≤p1,令q=(a*-sat(p,p1,p2))(p-sat(p,p1,p2)),很显然q是关于sat(p,p1,p2)的一条抛物线,所以当a*≤sat(p,p1,p2)≤p时q≤0.由于a < p,明显有a*≤sat(p,p1,p2)≤p成立.
当a>p时,证明方法和a < p时类似,在此不作赘述.
2 控制器设计本文考虑可参数化系统,也就是说,f(xk(t),t)虽然不能完全知晓,但f(xk(t),t)满足假设:
假设3 存在向量ϑT(t)(ϑ为r维列向量),使得函数f(xk(t),t)能够表述成:
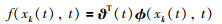
|
其中,ϕ(xk(t),t)是已知的非线性函数向量.
首先,对式(4)中的σk(t)求导:
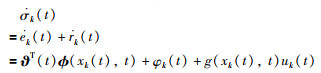
|
(5) |
其中,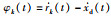
选择正定函数:
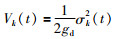
|
其中,gd是g(xd(t),t)的简写形式.
注2 在第1节中,在σk(t)函数中引入误差修正函数rk(t)主要有2个作用:1) Vk(t)函数满足Babalat引理的条件,即Vk(0)=0,使得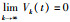
为了方便表达,简写函数:
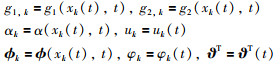
|
对Vk进行求导,并代入式(5)可以得到:
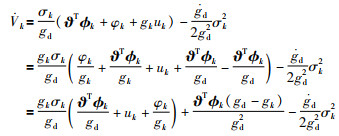
|
(6) |
对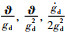
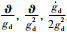
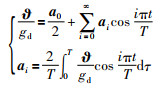
|
(7) |
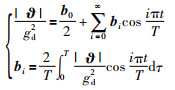
|
(8) |
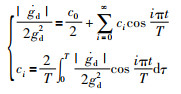
|
(9) |
式(7)~式(9)中的ai,bi和ci分别为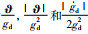
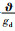
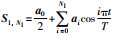
令误差函数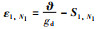
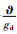
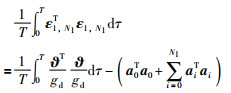
|
令:
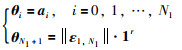
|
(10) |
其中,||·||表示无穷范数,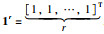
同理,令误差函数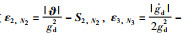
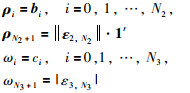
|
(11) |
显然,θi(i=0,1,…,N1+1),ρj(j=0,1,…,N2+1)和ωk(k=0,1,…,N3+1)皆为常数.
根据式(7)~式(11),在区间[kh,(k+1)h)上,式(6)可以进一步化简为
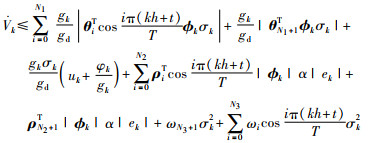
|
(12) |
根据上面的推导,提出下面的控制律来完成跟踪任务:
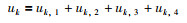
|
(13) |
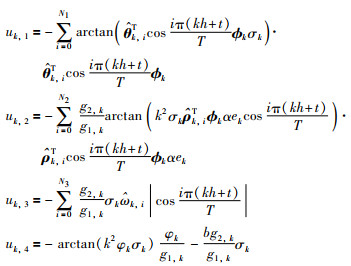
|
其中,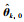
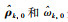
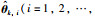
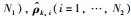
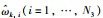
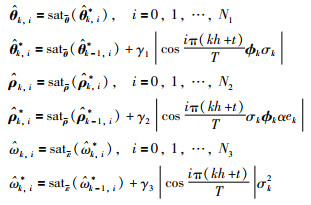
|
(14) |
其中,θi,ρi和εi分别是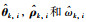
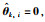
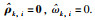
注3 在控制器设计过程中,如果事先知道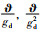
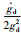
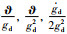
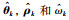
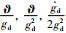
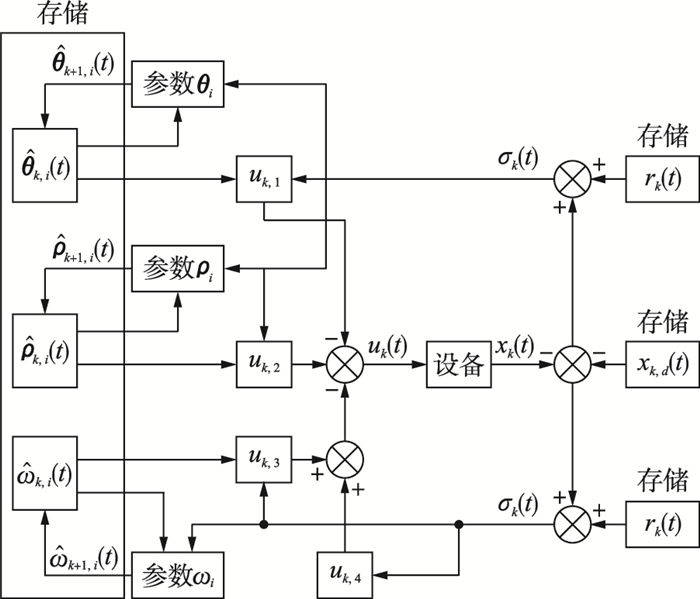
在传统自适应迭代学习控制中,虽然系统中的一些参数是时变量,但是这些时变量沿迭代轴来看是常量,所以可以采用自适应学习控制方法.在本文中,通过上述设计可知,学习思想下的自适应控制主要就将系统中的时变量通过傅里叶变换转换成一系列周期函数的叠加,并且这些周期函数的系数都是常数.算法中的学习量就是这些周期函数的系数,即常数,虽然系统跟踪的轨迹并不具有周期性或重复性,但并不影响参数的学习,因为经过变换后的系数是常数.该方法的控制示意图如图 1所示.
|
| 图 1 学习思想下的自适应控制示意图 Fig.1 Schematic diagram of adaptive control under learning ideas |
对于上一节设计的控制律和更新律,有如下的定理.
定理1 如果非线性系统(2)满足假设1、假设2和假设3,并且当k→∞时,控制律(13)和参数更新律(14)能够让系统(2)中的状态变量和误差滤波函数σk在区间[kh,(k+1)h)上一致收敛于0.
证明 考虑Lyapunov-like函数:
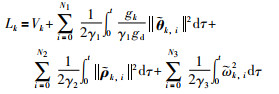
|
(15) |
其中,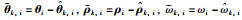
记ΔLk=Lk-Lk-1,则有:
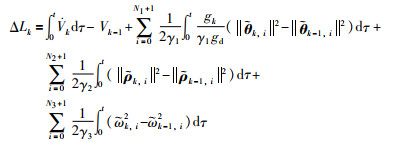
|
(16) |
考虑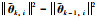
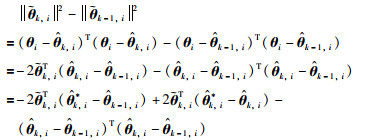
|
(17) |
根据引理1可得:
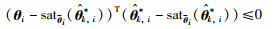
|
(18) |
根据式(14)和(18),式(17)可化简为
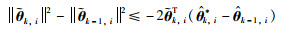
|
(19) |
利用同样的方法,可以得到:
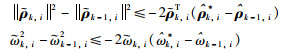
|
(20) |
将式(12)、式(19)和式(20)代入式(16):
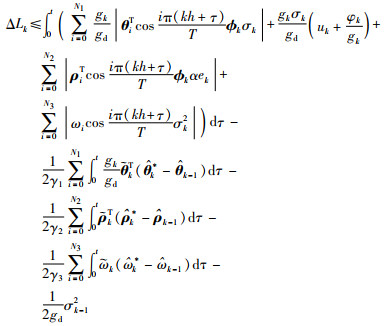
|
将式(13)代入上式可得
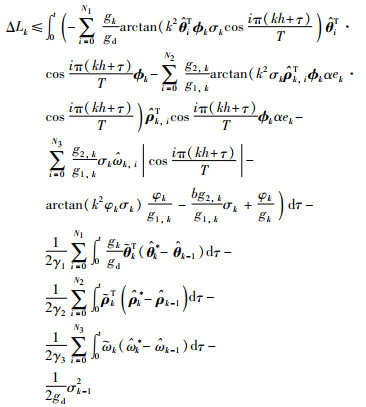
|
对于反正切函数arctanz,如果ε>0,则有|z|-z arctan(εz)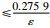
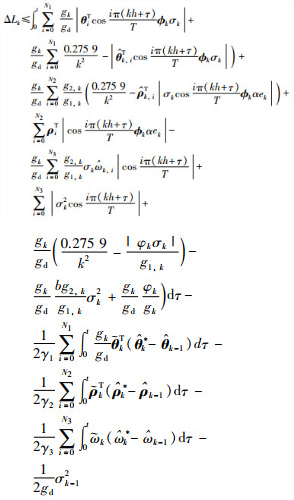
|
设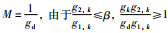
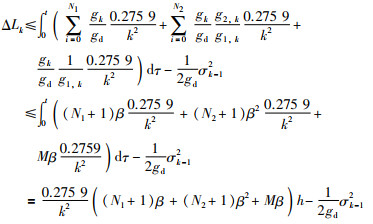
|
由于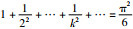
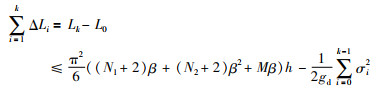
|
进一步化简可得
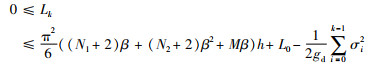
|
由于L0是非负有界量,并令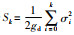
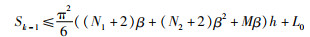
|
根据级数收敛的条件可知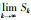
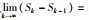
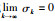
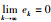
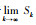
考虑非线性连续系统:
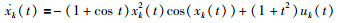
|
系统的作业区间为[0, 4].期望轨迹yd(t)=xd(t)=cos(0.5πt),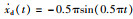
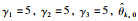
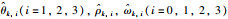
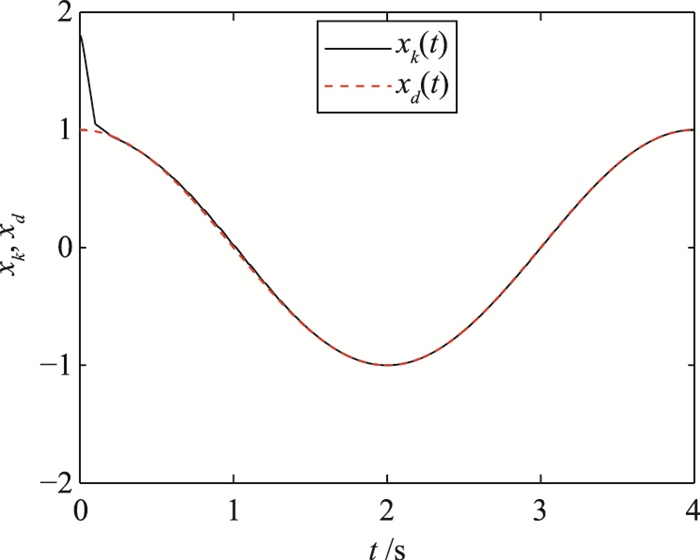
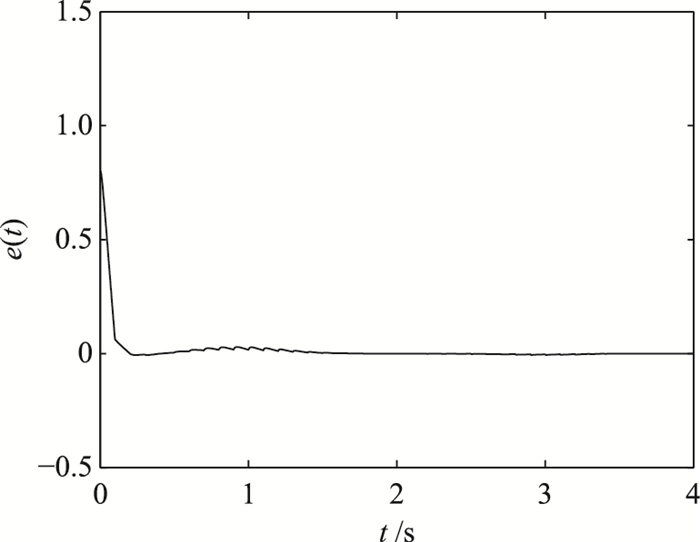
从图 2可以看出,控制律(13)在区间[0,0.1)上并没有完全修正好xk的偏差,经过若干个周期的状态偏差修正以后,xk才跟踪上期望轨迹xd.实际误差ek(t)如图 3所示.
|
| 图 2 实际轨迹xk(t)和期望轨迹xd(t) Fig.2 Actual trajectories xk(t) and desired trajectory xd(t) |
|
| 图 3 实际误差ek(t) Fig.3 Actual error ek(t) |
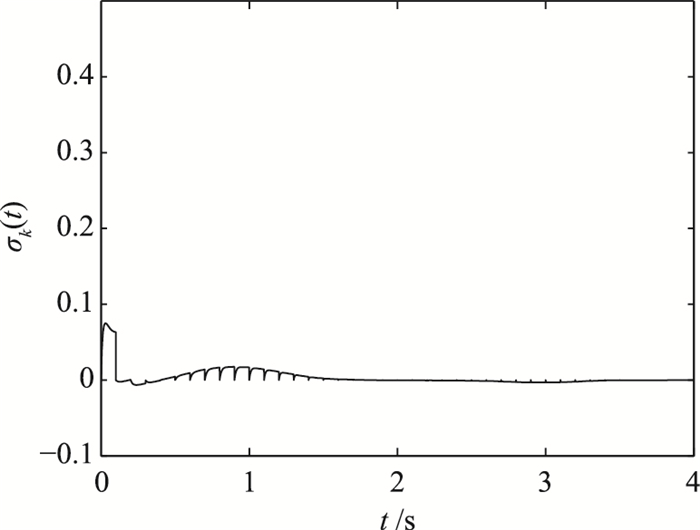
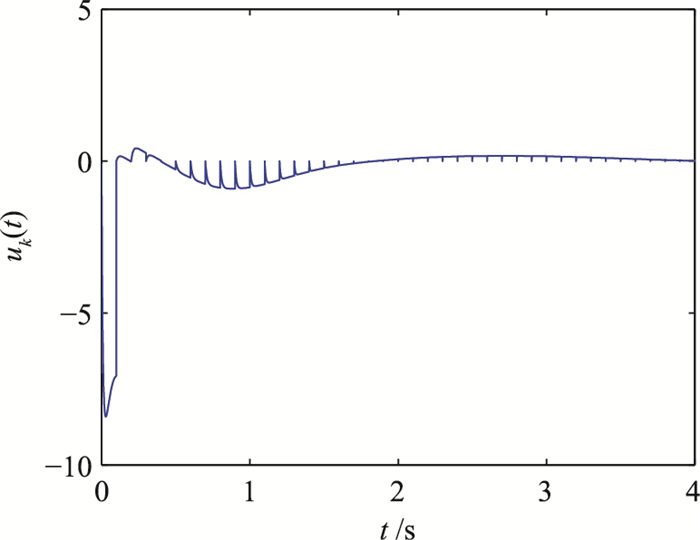
图 4和图 5中的变量在前半段每隔0.1 s会有一个突起,主要是因为滤波误差函数的修正周期为0.1 s,而且σk(0)=0,也就是说,每隔0.1 s会有一个类似于复位的操作.当完全跟踪上目标轨迹以后,这个复位操作的影响就不明显了.从图 4可以看出,若要求在很短的时间内修正较大的初态偏差,则要求必须提供较大的控制量.所以当状态偏差较大时,一般要求修正时间不能太短.
|
| 图 4 滤波误差σk(t) Fig.4 Filter-error σk(t) |
|
| 图 5 控制量uk(t) Fig.5 Control quantity uk(t) |
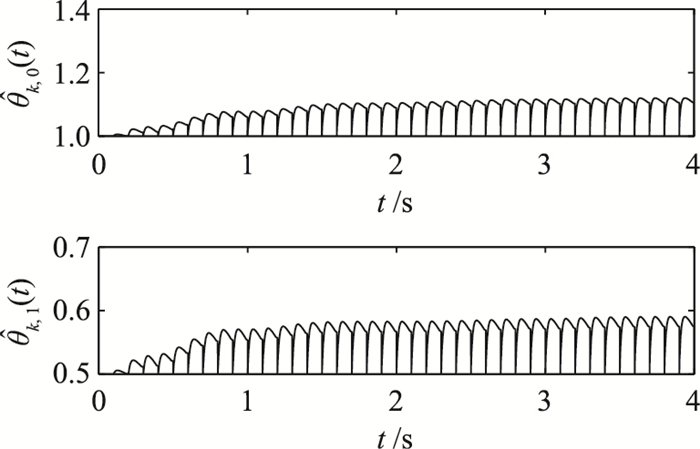
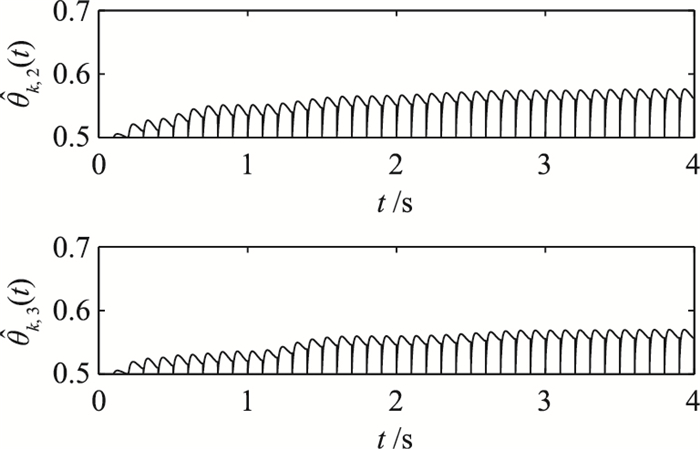
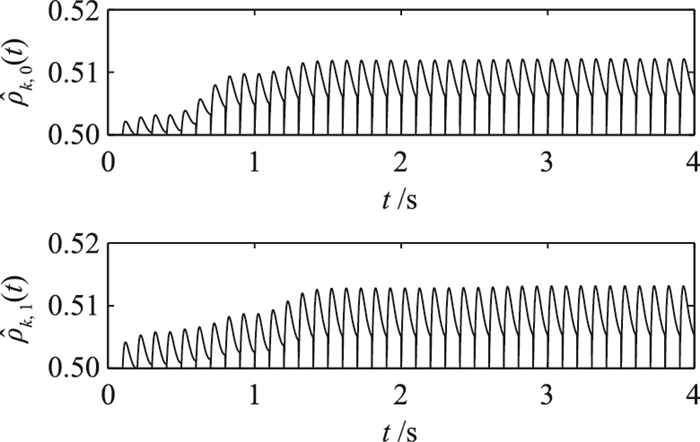
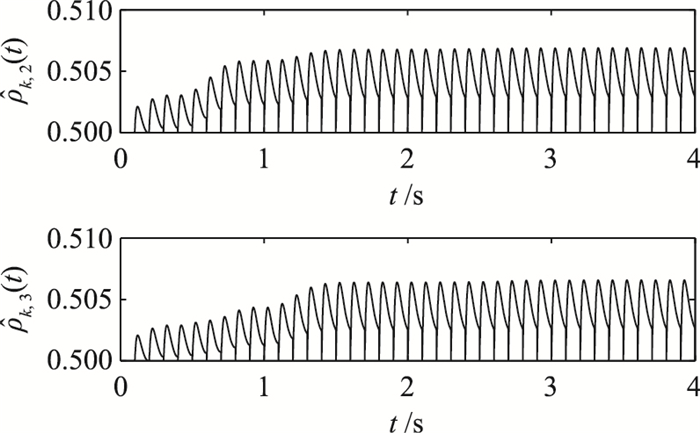
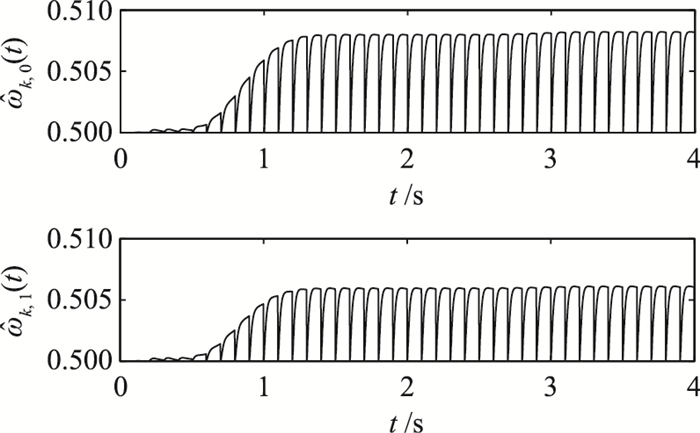
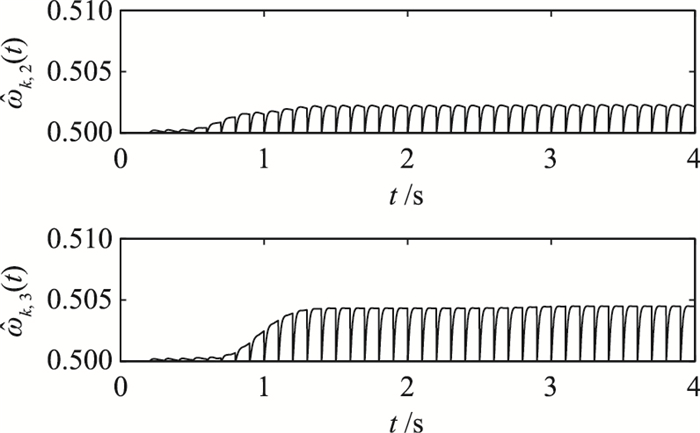
从图 6~图 11可以看出,所有参数在后期的各个子过程中基本呈现周期性,这主要是因为跟踪误差趋向于0,参数的调整量很小所导致.
|
图 6 参数  |
|
图 7 参数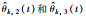  |
|
图 8 参数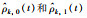 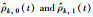 |
|
图 9 参数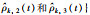 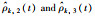 |
|
图 10 参数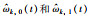 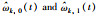 |
|
图 11 参数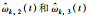 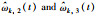 |
引用类似于文[25]中的算例,其动态模型为
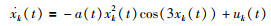
|
其中,a(t)=1+|sin t|,仿真过程中,系统的作业区间,期望轨迹xd(t)、系统初态、修正函数rk(t)、控制器增益b、参数更新律(14)中的γ1和γ2与算例1相同.由于本算例中的gd为常数,并且事先知道a(t)的界限,所以在进行估计时只需要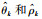
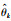
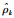
|
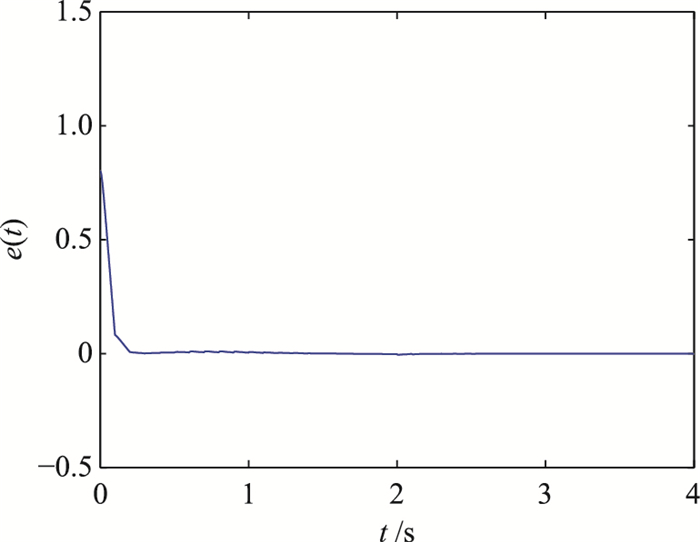
| 图 12 实际误差ek(t)(本文方法) Fig.12 Actual error ek(t) (the proposed method) |
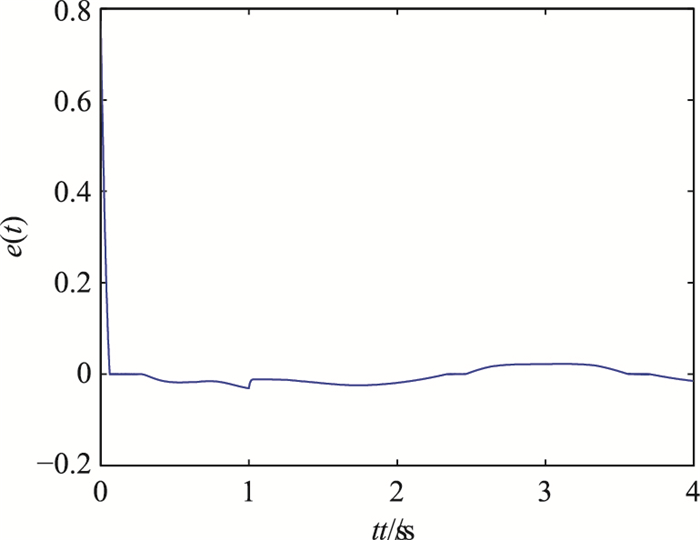
|
| 图 13 实际误差ek(t)(文[25]方法) Fig.13 Actual error ek(t) (The method in[25]) |
注4 若系统参数是未知常数,则所需要估计的参数就会减少,从而加快收敛速度;同样若增大b,γ1,γ2,γ3的值,缩短修正时间,也会加快收敛速度.从理论上说,如果不考虑控制量的限制,控制律(13)及参数更新律(14)能在较短的时间内将跟踪误差减小到任意小.
上面的仿真结果表明利用本文所提滤波误差函数设计的学习控制器可用于解决非线性连续系统任意初态误差的修正,而且这种方法设计的控制器具有较快的收敛速度和较高的控制精度,体现了该方法的有效性.
5 结论本文讨论了任意初态误差下非线性系统的自适应控制问题,在进行控制律设计时运用了学习控制的思想,提出了一种带有误差修正项的自适应控制策略.该算法将被控过程分成若干个等长时间的子过程,在每一个子过程中都会进行初态误差的修正,直到完全跟踪为止.并且在每一个子过程中还会进行参数学习,以便加快收敛速度.在控制过程中,利用反正切函数对控制量进行连续化处理,解决了控制过程中的颤振问题(子过程的边界点除外).在分析算法时借助无穷级数收敛的条件证明误差能够收敛,相应变量有界.最后的仿真算例验证了算法的有效性.
| [1] | Arimoto S, Kawamura S, Miyazaka F. Bettering operation of robots by learning[J]. Journal of Robotic Systems, 1984, 2(1): 123–140. |
| [2] | Bristow D A, Tharayil M, Alleyne A G. A survey of iterative learning control[J]. IEEE Control Systems Magazine, 2006, 3(26): 96–114. |
| [3] |
许晖敏, 田森平.
一类广义系统的二阶迭代学习控制算法[J]. 信息与控制, 2018, 47(6): 745–749.
Xu H M, Tian S P. Second-order iterative learning control algorithm for singular systems[J]. Information and Control, 2018, 47(6): 745–749. |
| [4] |
逄勃, 邵诚.
基于奇异值分解的PID型参数优化迭代学习控制算法[J]. 信息与控制, 2014, 43(4): 483–489.
Pang B, Shao C. PID-type parameter optimal iterative learning control algorithm based on singular value decomposition[J]. Information and Control, 2014, 43(4): 483–489. |
| [5] |
陶洪峰, 沈建强, 杨慧中.
一类不确定性离散非线性重复过程的迭代学习容错控制[J]. 信息与控制, 2019, 48(1): 88–96.
Tao H F, Shen J Q, Yang H Z. Iterative learning fault-tolerant control for a class of uncertain nonlinear discrete repetitive processes[J]. Information and Control, 2019, 48(1): 88–96. |
| [6] |
许建新, 侯忠生.
学习控制的现状与展望[J]. 自动化学报, 2005, 31(6): 943–952.
Xu J X, Hou Z S. On learning control:The state of the art and perspective[J]. Acta Automatica Sinica, 2005, 31(6): 943–952. |
| [7] | Chien C, Hsu C, Yao C. Fuzzy system-based adaptive iterative learning control for nonlinear plants with initial state errors[J]. IEEE Transactions on Fuzzy Systems, 2004, 5(12): 724–732. |
| [8] |
孙明轩.
有限时间迭代学习控制[J]. 系统科学与数学, 2010, 30(6): 733–741.
Sun M X. Finite-time iterative learning control[J]. Journal of Systems Science and Mathematical Sciences, 2010, 30(6): 733–741. |
| [9] | Yin C K, Xu J X, Hou Z S. A high-order internal model based iterative learning control scheme for nonlinear systems with time-iteration-varying parameters[J]. IEEE Transactions on Automatic Control, 2010, 55(11): 2665–2670. |
| [10] |
严求真, 孙明轩, 蔡建平.
迭代学习控制的参考信号初始修正方法[J]. 自动化学报, 2017, 43(8): 1470–1477.
Yan Q Z, Sun M X, Cai J P. Reference-signal rectifying method of iterative learning control[J]. Acta Automatica Sinica, 2017, 43(8): 1470–1477. |
| [11] | Chi R H, Hou Z S, Xu J X. Adaptive ILC for a class of discrete-time systems with iteration-varying trajectory and random initial condition[J]. Automatica, 2008, 44: 2207–2213. |
| [12] |
李国军, 陈东杰, 韩一士.
带有初态误差的高阶多智能体系统一致性跟踪[J]. 应用数学学报, 2018, 41(2): 156–171.
Li G J, Chen D J, Han Y S. Consensus tracking of high-order multi-agent systems with initial state errors[J]. Acta Mathematicae Applicatae Sinica, 2018, 41(2): 156–171. |
| [13] | Li X D, Chow T W S, Ho J K L, et al. Iterative learning control with initial rectifying action for nonlinear continuous systems[J]. IET Control Theory and Applications, 2009, 1(3): 49–55. |
| [14] |
冯纯伯.
自适应控制的理论及应用[J]. 控制理论与应用, 1988, 5(3): 1–12.
Feng C B. Theory and application of adaptive control[J]. Control Theory & Applications, 1988, 5(3): 1–12. |
| [15] |
吴宏鑫.
自适应控制技术的应用和发展[J]. 控制理论与应用, 1992, 9(2): 105–115.
Wu H X. Application and development of adaptive control technology[J]. Control Theory & Applications, 1992, 9(2): 105–115. |
| [16] |
李军, 石青.
基于ELM的一类不确定性纯反馈非线性系统的Backstepping自适应控制[J]. 化工学报, 2016, 67(7): 2934–2943.
Li J, Shi Q. Adaptive control for a class of uncertain pure-feedback nonlinear systems using backstepping based on extreme learning machine[J]. Journal of Chemical Industry and Engineering, 2016, 67(7): 2934–2943. |
| [17] |
王璐, 郭毓, 钟晨星, 等.
控制力矩陀螺框架伺服系统期望补偿自适应鲁棒控制[J]. 控制理论与应用, 2017, 34(9): 1143–1150.
Wang L, Guo Y, Zhong C X, et al. Desired compensation adaptive robust control for control moment gyroscopes gimbal servo system[J]. Control Theory and Applications, 2017, 34(9): 1143–1150. |
| [18] |
杨一岱, 荆武兴, 张召.
一种挠性航天器的对偶四元数姿轨耦合控制方法[J]. 宇航学报, 2016, 37(8): 946–956.
Yang Y D, Jing W X, Zhang Z. A new method for orbit and attitude coupling control problem of flexible spacecraft based on dual quaternions[J]. Journal of Astronautics, 2016, 37(8): 946–956. |
| [19] | Sadegh N, Horowitz R, Kao W, et al. A unified approach to the design of adaptive and repetitive controllers for robotic manipulators[J]. ASME Journal of Dynamic Systems, Measurement, and Control, 1990, 112(4): 618–629. |
| [20] | Kuc T, Lee J S. An adaptive learning control of uncertain robotic systems[C]//30th IEEE Conference on Decision and Control. Piscateway, NJ, USA: IEEE, 1991: 1206-1211. |
| [21] | French M, Rogers E. Non-linear iterative learning by an adaptive Lyapunov technique[J]. International Journal of Control, 2000, 73(10): 840–850. |
| [22] | Xu J X, Tan Y. A composite energy function-based learning control approach for nonlinear systems with time-varying parametric uncertainties[J]. IEEE Transactions on Automatic Control, 2002, 11(47): 1940–1945. |
| [23] |
陈为胜, 李俊民.
全局稳定的分散自适应神经网络反推跟踪控制[J]. 控制与决策, 2009, 24(6): 819–824.
Chen W S, Li J M. Globally stable decentralized adaptive neural network backstepping tracking control[J]. Control and Decision, 2009, 24(6): 819–824. |



